基于不确定度分析的动态校准系统设计
2018-01-18孟晓山杜红棉
孟晓山,杜红棉,杨 帆
(中北大学 电子测试技术国家重点实验室 仪器科学与动态测试教育部重点实验室,太原 030051)
冲击波超压是评估武器毁伤威力的重要指标之一,冲击波超压相关参数的测量为武器的研制提供了重要依据[1],因此这些参数的准确测量尤为重要。瞬态特性是冲击波超压信号的突出特点,要求测试系统有很好的瞬态响应特性。这属于动态测试的范畴,所以常以瞬态信号进行动态校准,以确定测试系统的动态特性是否满足待测冲击波信号的要求[2]。目前常用不确定度表征测试结果的准确性[3]。动态校准过程具有复杂性和时变性,因此决定了动态校准不确定度相对于一般校准系统更复杂[4]。
激波管是常用的冲击波超压校准装置[5]。采用激波管校准测试系统的动态灵敏度时,由于部分分量的不确定度导致测试系统动态灵敏度存在不确定性[6-7]。根据不确定度的来源[8],对校准过程中的不确定度分量进行分析,为了减少不确定度的影响,设计了采集校准系统及上位机软件,并进行了仿真实验。
1 激波管校准装置的原理
激波管校准装置的结构示意如图1所示。该装置主要由高压气瓶、激波管、测速传感器、被测压力传感器和数据采集系统组成。其中,激波管是一根两边封闭的长管,根据所需要的阶跃压力值选择中间膜片的材料和厚度,中间膜片将激波管分为高压室和低压室两部分。在进行校准实验前,需对高压室进行充气准备,低压室一般为101.325 kPa(1 atm),且在低压室放置待校准的传感器和测速传感器。当高低压室气体压强超过膜片能承受的极限值时,膜片破裂,形成激波[9]。冲击波通过距离为L的2个测速传感器得到了时间间隔t,之后对被校传感器作用。

图1 激波管校准装置结构示意Fig.1 Shock tube calibration device structure diagram
被校传感器安装在激波管端面,测得的是反射压力,也可以安装在传压管道的侧面用于测量掠入式压力。将传感器安装在激波管端面时,会因为计算反射阶跃压力存在的不确定度而导致计算压力传感器动态灵敏度不准确,故在此对反射压力进行不确定度的分析。实验室现有的激波管如图2所示,其管长10 m,内壁直径100 mm,最大反射压10 MPa。

图2 激波管实物照片Fig.2 Shock tube physical map
激波管动态压力校准系统计算传感器灵敏度K为[10]

式中:ΔP为输入的阶跃压力值;B为测试系统通过读数软件读出的幅值。
由式(1)可知,由ΔP和B可以计算出传感器动态灵敏度K,而ΔP是激波管校准系统不确定度的主要因素。低压室底端反射阶跃压力为
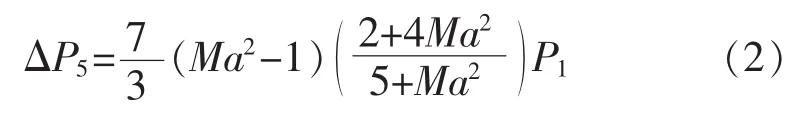
其中入射激波马赫数Ma为

式中:vs为激波速度;a为空气中音速,激波的传输介质为空气;T为激波管内气体温度;L为2个测速传感器之间的距离;t为激波经过2个测速传感器之间的传输时间。
由式(2)可知,空气冲击波反射超压ΔP5的不确定度,由激波管内的L、T、t以及低压室的初始压力值P1等分量共同决定。根据不确定度的传递模型,ΔP5与4个有关分量的传递公式为

式中:各分量对应的灵敏度系数分别为

2 不确定度分量的对比分析
根据各参数相关资料及仪器设备的校准证书,分别对以上各个因素进行分析。以下参数均假设管内气体为理想气体,取P1=0.089 MPa,为低压腔体内的气体压力;T=20.1℃,为腔内气体温度;C0=332 m/s,为0℃条件下声音在理想空气中的传播速度;L=0.55 m,为 2 个测速传感器间距;t=932 μs,为通过距离L长度激波的传播时间。综合以上各个实际或理想参数,得出激波管马赫数Ma=1.716。
间距测量引入的不确定度分量uL主要受激波管结构体安装位置和传感器配置公差及测量传感器间距的仪器精度的影响。距离测试仪可以准确测量到1×10-4m,此误差为极限误差,可看作服从均匀分布,则:
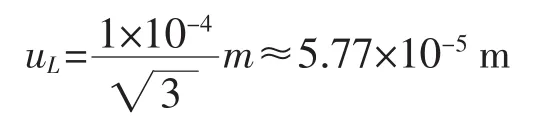
激波传播时间测量引入的不确定度ut由连接测速传感器采集卡的采样频率引起,采样频率为fs,则ut=1/fs。假设采集卡采样频率为1 M,不确定度ut=1 μs;当采集卡的采样频率为2 M时,不确定度ut=0.5μs。
温度测量引入的不确定度分量uT由温度记录仪的仪器精度所致。目前温度记录仪的精度可以达到0.01℃,故不确定度分量uT=0.01℃。
压力测量仪在低压段压力测量时引入的不确定度uP由压力测量仪引起,测量精度可以达到0.001 MPa,在实际测试中可看作一个严格的均匀分布,则

数据采集系统分辨力引入的不确定度分量u5与模/数转换器的输入输出电压范围和位数有关。在此分别选用14位和16位的。A/D转换器进行分析:
(1)选择14位芯片 AD5734,电压测量范围为-10~10 V,则数据采集系统的分辨力为

最大误差区间半宽度a2=0.5 LSB=0.0006 V,则不确定度为

(2)16位选择芯片AD5761,对应的电压测量范围为-5~5 V,则数据采集系统的分辨力为
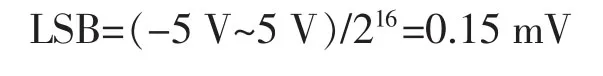
分辨力造成的误差在(-0.5 LSB,0.5 LSB)范围内服从均匀分布,最大误差区间半宽度a2=0.5 LSB=0.075 mV,则有不确定度为

根据以上计算,在选择测量仪器精度最高的情况下,对以上分量进行分析,如表1所示。

表1 反射超压不确定度分量Tab.1 Reflection overpressure uncertainty component
根据表1对比可知,采样频率为1 M和2 M对反射超压ΔP5不确定度基本无影响,但是,模/数转换器的选择对反射压力ΔP5不确定度影响较大。因此,为了减小反射超压ΔP5不确定度,在采集系统中可以设置采样频率为1M,选择16位的模/数转换器。
3 动态校准系统的设计
根据以上对校准装置的不确定度分析,设计了整套动态校准系统及上位机软件。采集系统信号流程如图3所示,激波管产生的阶跃信号作用于被校压力传感器,传感器经过适配电路将接收到的压力信号转换为电压信号,经过滤波放大电路后输送到模/数转换器进行转换,最后将数字信号存入由FPGA控制的Flash芯片。整个采集系统由智能电源为模拟及数字电路部分供电,最后通过USB接口将数据读取到上位机上。校准系统上位机功能模块如图4所示。

图3 数据采集系统Fig.3 Data acquisition system
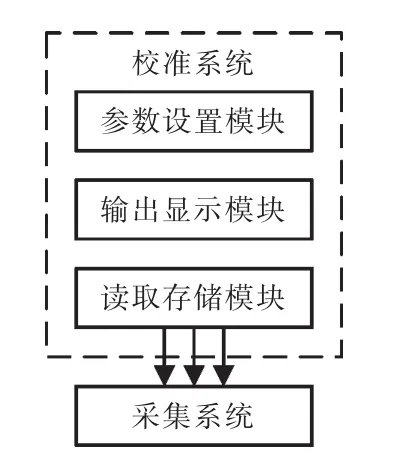
图4 校准系统上位机模块Fig.4 Upper computer module of calibration system
4 动态校准实例
选用2支PCB公司的113B03型测速传感器和1支113A24型压力传感器。将传感器安装在激波管的相应位置,相关参数填入上位机界面,用USB读数装置与PC相连,然后点击运行。上位机显示界面分别如图5~图7所示。
此次实验测得,测速传感器得到的时间间隔为891 μs,由此可以计算出入射激波马赫数为1.81,进而得到反射阶跃压力为0.8474 MPa。由图7可知,超压峰值为661 mV,故此次实验得到的压力传感器动态灵敏度为2.797 mV/kPa。

图5 传感器设置界面Fig.5 Sensor settings interface

图6 激波管环境设置界面Fig.6 Shock tube environment settings interface

图7 显示界面Fig.7 Display interface
5 结语
对压力动态校准系统不确定度分量进行了定量分析,并分析了不同条件下对反射超压ΔP5不确定度的影响。由此得出,采样频率的大小对不确定度基本无影响,而采集系统的分辨力大小对不确定度影响较大。为了降低2个分量的影响,设计了一款采样频率和模/数转换分辨率适合的动态校准系统及上位机软件,并进行了仿真实验。
[1]胡宝奎.一种冲击波超压无线式存储测试系统的研究[D].太原:中北大学,2010.
[2]轩春青,轩志伟,赖富文.压力传感器测试系统的动态校准及特性分析[J].传感技术学报,2015,28(7):982-986.
[3]刘智敏.不确定度及其实践[M].北京:中国标准出版社,2000.
[4]李慧奇,王凯红,李思.基于动态测量理论的数据处理和不确定度评定[J].电测与仪表,2015,52(22):80-84.
[5]原玢.冲击波超压测试系统的动态不确定度研究[D].太原:中北大学,2012.
[6]李强,王中宇,王卓然.压力传感器动态校准不确定度评定[J].北京航空航天大学学报,2015,41(5):847-856.
[7]张大有.激波管在压力传感器动态性能校准和实验上的应用[J].宇航计测技术,2004,24(4):24-27.
[8]刘智敏.测量不确定度及其应用[J].计量技术,2001,35(6):46-49.
[9]张近,李守彦,席葆树.压力测量系统的激波管动态校准[J].传感器技术,1989,8(1):44-47.
[10]余尚江,李跃波,曾辉,等.基于激波管校准的传感器动态灵敏度试验研究[C]//第十二届激波与激波管会议论文集.北京:中国力学学会,2006:358-361.一般为0.69 MPa,指数a为特定阀门的常数,如对于单级直通阀,初始破坏系数范围内的a值为 0.10~0.14[6];尺寸整定系数 SSE=[d/dR]b,b=0.068( Cv/d2)1/4,d为阀门内径。需要指出的是,
