中考试卷研究：整体解读与局部剖析

杨剑峰

[摘 要] 教师对中考试卷的研究应是多维的. 当然，我们不能只在研究上下功夫，因为研究仅为发展学生的数学核心素养提供了可能，如果没有扎根于课题的整体规划，再好的研究成果也不可能转化为教学生产力，不能为学生的發展服务.

[关键词] 中考试卷；整体解读；局部剖析

研究中考试题，是教师“获取教学素材，服务学生发展”的重要途径. 在近期的一次市级研讨活动中，笔者结合近五年徐州市中考数学卷分享了自己中考试题研究的一般步骤与价值指向，引发了参研教师的热议. 现将笔者分析这五份中考卷的历程与各位做个交流，希望能给大家一些启示.

通读，感知试卷结构

拿到一份中考试卷，我们首先要关注的是考试时间、总分、题型、题量等组卷要素. 任何一次中考命题，各门学科的考卷设置都会从卷面上提出明确且相对固定的要求，这些明确且相对固定的要求不仅影响着中考，还影响着我们的日常教学. 无论是日常教学，还是阶段性考试，我们都应按照这些要求来组织教学、实施考试，以保证阶段教学与终结性考试精准对接，让学生的能力和素养在考试中得到极致发挥. 为此，笔者通读了近五年的徐州市中考数学试卷，并将一些重要的数据梳理出来制作成了表1.

通过表1中的数据我们不难发现，近五年，徐州中考数学试卷的答题时间均为120分钟；全卷总分均为140分；试题总量大题数完全一致，都是28题，而小题数有一定的差异，最多的是2015年的43题，最少的是2014年和2018年的39题. 五年的考试题型都是选择题、填空题和解答题三种类型，题量是固定的，选择题均为8题，填空题均为10题，解答题均为10个大题. 且三种题型的总分也是固定不变的，选择题3分一题，总分24分；填空题3分一题，总分30分；解答题总分86分. 从考试时间、分值、题量、题型等方面来看，近五年徐州中考数学试卷的变化不大，于是我们不妨进行一个大胆的预测：接下来的中考，徐州卷依然会沿袭近几年的风格，上述组卷要素不会发生太大的变化.

分解，理清板块归属

解读全卷的结构，除了要解读上面所说的组卷要素外，还应结合教材与课标进行考查内容归属板块的解读，弄清考卷中数与代数、图形与几何及统计与概率部分试题的题量、分值及题型分布情况，为今后知识教学的准确定位和试题命制方向找到基本依据. 表2是笔者按照流程对2014—2018年徐州市中考数学试题归属板块进行梳理后制成的.

表2呈现的是各板块徐州中考数学试卷近五年试题的数量、归属题型及分值情况. 结合表格我们不难看出，近五年的徐州中考数学试卷对课标规定的三个板块的分值和题量是基本固定的：数与代数，约16小题，62分左右；图形与几何，约17小题，57分左右；统计与概率，约7小题，21分左右. 这样的试题数量与分值安排，与我们所用的苏科版教材给出的教学课时的比例是完全匹配的. 试想，中考试卷都能按照这样的比例进行设计，那我们的日常教学课时分配和阶段测试的试题安排，不也应该按照此比例进行安排或设计吗？

梳理，明晰基本考点

对于中考试题的命制，命题人首先要对义务教育阶段学生应知应会的知识进行全面梳理，然后通过知识点情境的嵌入形成具有普适性的原创考题，最后通过整体布局形成考卷. 显然，中考试题指向的是学生获得的数学“四基”，是对学生所获显性知识（基础知识与基本技能）与隐性知识（基本思想和基本活动经验）的直接考查，其考查的面是初中学段，考查的点广泛分布于初中三个年级的每一个单元之中. 所以，细致的考点梳理能较为清晰地梳理出初中阶段的知识脉络，能让我们在明晰中考基本考点的同时，知晓这些考点（知识点）的教学要求.

那么，怎样的考点梳理才能称之为细致入微呢？笔者以为，首先应详细剖析每一道考题的考点. 可通过对试题解答所需的知识点进行细致分析，形成当年的单题考点分析表. 可将当年的单题考点分析表同前几年所做的单题考点分析表拼接到一起，对同一考点出现的频次进行详细统计，理清其出现的次数与位置. 接下来，便是对同一考点出现的频数及位置的内涵进行解读. 考查的次数较多，说明知识点为命题者所高度重视，应该是初中阶段较为重要的知识，如果该考点恰好又处于容易题或中等题的位置上，这足以说明该知识点属于初中阶段基础知识中的重要知识，应引起我们的重视，教学中便需要我们花大力气，从学生的认知起点处就展开渐进式巩固与提升，使之不断出现在学生的数学知识获得与巩固过程之中，力求通过不断反复的强化训练形成知识的固化效应. 如果考查的次数较少，说明考点为边缘知识，其虽然在我们的教学范围之内，但考查要求较低，所以我们对这些知识的教学不应耗费太多的时间和精力. 但有一点值得我们注意：边缘知识虽考查次数较少，但也会考查，所以在总复习阶段，此类知识也不可缺席，也就是说，在中考总复习阶段，任何一个初中学段学过的数学知识都不可缺席. 因此，我们的数学教学要将每一个概念的教学作为知识向能力、素养转化的起点，当每一个新知出现时，我们要站在促进每一个个体素养发展的角度设计与实施教学，确保普惠教学在起点处有效展开，并取得应有的成效.

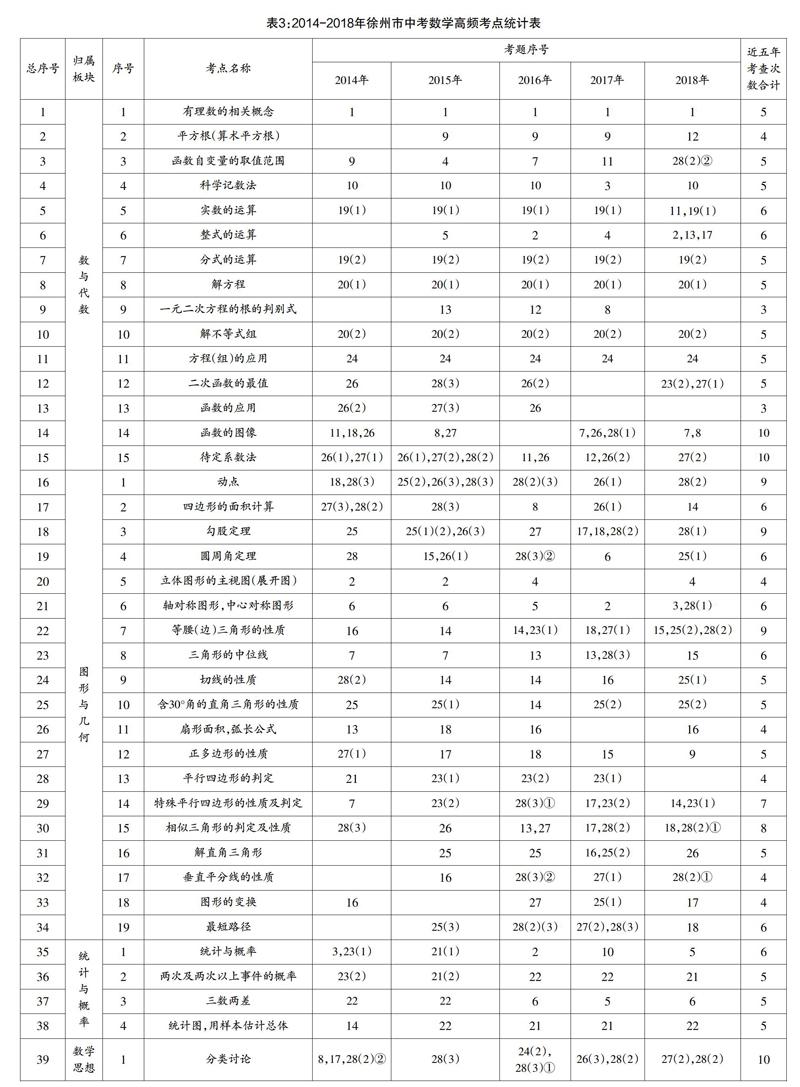
从表3中我们不难发现，近五年中考中很多的知识点都是连续出现的，有些知识点在同一份试卷中甚至出现了2次、3次. 如2015年卷的25题（1）（2）和26题（3）均考查了勾股定理，同样还是在这份试卷中，第15题和第26题第（1）问反复考查了圆周角定理. 这样的反复考查，充分说明这一知识对学生数学素养的发展是何等重要，这也给我们的日常教学、试题命制及复习迎考带来了启示：在关注“面”的同时，还要注意“点”. 对于常考的知识，如上面的勾股定理、圆周角定理、数与代数中的基本概念及相关运算、几何图形的性质与判定等，我们在教学中应高度关注，并在获取、应用等环节上给予每一名学生多一些的自主探索时间与空间，让他们在获得知识的同时，能够积累个性化学习与应用的经验.

这样的考题研究有着丰富的内涵和明确的方向，对本学段普惠教学的落实无疑大有裨益. 中考试卷对所有参加考试的学生都适用，其考查的是所有学生的数学学习状况，这就要求我们的教学应如试题命制一样做到“面向全体学生”. 为了让所有学生获得最大的发展，我们应通过中考试题的考点梳理，确保考点全覆盖的前提下，在学生应知应会的知识上多下功夫，努力找寻常规教学的起点，确保知识教学与技能训练符合学生的发展需求，顺应学生的发展规律，既不人为拔高，也不私自降低，确保他们能够在合适的时间点上获得适合的知识，形成适切的技能.

详析，解读关键考题

中考，很多地方将招生考试与毕业考试进行了合并，这就要求除了具有普适性外，中考卷还应具有选拔性. 既然是选拔，就必须让学生在问题解决上呈现一定的差异性，从而彰显出试卷的区分度. 具体到考卷上，能够体现差异性的也就有限的几道题. 以徐州中考数学考卷为例，有明显差异性的一般有5道题：第8题（选择题最后一题），第18题（填空题最后一题），第26、27、28题（解答题的后三题）. 这些考题一般涉及的知识点都比较多，知识点之间的连接也较为巧妙，如果没有完整的知识网络、扎实的推理功底、丰富的建模经验和强大的运算能力，想在短暂的时间内顺利得解，绝非易事. 简单来说，就是要学生具备较高的数学素养，才能“化解问题，成就高分”. 因此，本学段的数学教学不仅要关注基础知识、基本技能这些显性知识的教学，还应重视常用基本解题方法的归纳和解题套路的建构. 此外，还要在数学基本思想和基本活动经验上花些功夫，以便学生遇到问题可以展开直观想象，将题目信息与自身认知系统中某一个认知点产生关联，从而获取问题解决的绝佳路径. 然而，学生“灵机一动”这根弦绝非轻而易举就可以触动的. 能在紧张的考试氛围下迅速激活学生的思维，一方面需要长期坚持地对认知系统进行充实与完善；另一方面，应重视对中考卷中关键考题的研究，为学生积累关键题的基本解决套路和解题经验. 这种研究，不能仅仅停留在知识点分析的层面上，我们要对试题进行深挖，挖掘出学生在问题解决过程中需要的知识应用点、情感投入点和意志支撑点，从而确定解答此类压轴问题学生所必须具备的数学核心素养，这也是我们日常教学中必须融入教学进程加以着力发展的核心素养.

分析徐州市近五年的核心考题给了笔者这样的启示：数学核心素养广泛分布于我们的教学进程之中，学生的每一次问题思考和问题解决都是发展核心素养的機遇，教师应着力于解题一般方法和常用套路的归纳，让学生在获得方法套路的过程中形成和发展包含知识、技能、情感、态度及价值观等多种要素的核心素养：数学抽象、逻辑推理、数学建模、直观想象、数学运算、数据分析.

研究中考试卷，除了要详细剖析、解答考题所需的基础知识和基本技能，还要分析解答考题所需的必备能力，它们都是核心素养得以“丰腴”的根本保证. 没有能力的支撑，学生的核心素养发展速度是缓慢的，发展成果必将是单薄的. 我们同样应该关注解答考题所需的情感要求，解答数学题不仅需要知识与能力，同样离不开丰富的情感融入. 情感是核心素养发展的核心动力，没有情感的加盟，素养发展将成为一句空话……

？摇？摇显然，教师对中考试卷的研究应是多维的. 当然，我们不能只在研究上下功夫，因为研究仅为发展学生的数学核心素养提供了可能. 如果没有扎根于课题的整体规划，再好的研究成果也不可能转化为教学生产力，不能为学生的发展服务. 所以，研究虽重要，但规划与落实更重要. 当我们完成对中考试题的多维研究后，设计分步实施素养发展的方案就显得尤为重要了.