资源重组,因材施教
2018-01-17江炜炜
江炜炜


[摘 要] 学材再建构是基于学生发展需要、教学实施需要而进行的资源再加工、再组合,真正的再建构可以更符合教学内容的目标达成,更符合学生发展的需要. 为此,在学材再建构的实践与研究中,教师必须深入学生学情,深入研究教材,达到课堂教学的最优化.
[关键词] 学材再建构;资源重组;三角形的中位线
“学材再建构”源自李庾南老师倡导的“自学·议论·引导”教学法,是指教师为了提高学习的效益,主动对各种主客观性学材和资源进行加工和重组,以更好地适应学生,提高教学的效率. 在近期的一次培训中,笔者有幸聆听了李老师关于“学材再建构”的讲座,受益颇多. 下文以“三角形的中位线”的教学片段为例,谈谈笔者对该种教学法的理解,供各位同仁参考.
教材分析
教材是最主要的学材,传统的教学是按照课本顺序进行的教学设计,“学材再建构”则是一种对传统教学的颠覆,一切为了学生的效益,使教学尽最大可能适应学生. “三角形中位线”的教学是利用平行四边形的性质研究三角形中的特殊线段,因此教材将此安排在“平行四边形的性质”一节之后,课本资源较少. 鉴于以往在讲授这部分内容时学生更多的是接受式学习,并不能很好地掌握其实质,笔者将该内容移至章末,在学生学习完“特殊四边形”以后探讨,使学生有更为扎实的平行四边形知识作为铺垫. 并且将此内容与“中点四边形”结合,让学生在掌握三角形中位线性质的基础上探讨中点四边形的性质,将两节课合并为一节课,提高教学效率.
在进行了资源重组以后,笔者将本节课的教学目标定为:
1. 掌握三角形中位线的定义,理解三角形中位线的性质;
2. 灵活运用三角形中位线的性质推导中点四边形的性质;
3. 感受三角形中辅助线的添加原则和中点个数的关系.
教学重点是:理解三角形中位线的性质.
教学难点是:三角形中位线性质的推导及证明.
教学片段
1. 创设情境,引入教学
引入教学环节在新授课中占有极其重要的地位,引入的成效直接关系到学生对这节课内容的兴趣及探究欲望的高低. 创设良好的情境,吸引学生的无意注意,将学生的注意力迅速吸引至课堂中,有利于教学的开展.
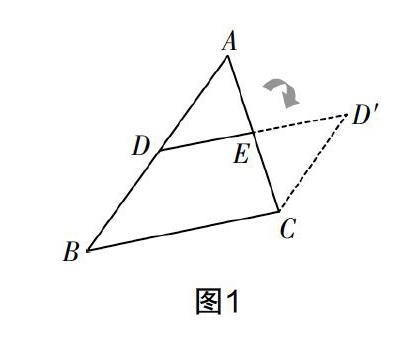
学材一(活动探究):取出三角形纸片(课前已准备好),用剪刀将三角形纸片剪一刀,使剪痕平行于三角形的一边,将三角形纸片分割成一个三角形和一个梯形,并观察:
(1)剪得的两张纸片能否拼成一个平行四边形?
(2)若要使拼成的图形是一个平行四边形,那么剪痕与三角形另外两边的交点应在什么位置?
(完成方式:学生自主探索,后全班交流展示)
学生通过探索,得出结论:如果沿着三角形两边的中点将三角形纸片剪成两片,则剪得的两张纸片可以拼成一个平行四边形.
2. 猜想证明,形成定理
数学是一门严谨的学科,我们要求学生对知识的掌握不仅要“知其然”,而且要“知其所以然”,在定理的教学中,让学生自己猜想,再对自己的猜想加以验证,一方面有利于学生对定理的理解,另一方面可以提高学生的逻辑思维能力.
师:如图2,△ABC中具备上述特征的線段叫作“三角形的中位线”,你能给中位线下一个定义吗?
师生共同揭示定义:连接三角形两边中点的线段叫作三角形的中位线. 并对定义进行补充:一个三角形共有三条中位线.
师:如图3,在△ABC中取BC的中点D,连接AD,这样的线段叫什么?
生:三角形的中线.
师:三角形的中线和中位线仅有一字之差,那么它们有何相同点和不同点呢?
生:相同点是它们都和中点有关,不同点在于中线取一边的中点,而中位线取两边的中点.
观察猜想:△ABC的中位线DE与第三边BC有怎样的关系?
教师通过几何画板演示,改变△ABC的形状及大小,追踪的变化,师生共同形成猜想:位置关系:DE∥BC,数量关系:DE=BC.
证明猜想:已知△ABC中,D,E分别是AB,AC的中点,求证:DE∥BC,DE=BC.
(完成方式:学生小组合作探究后全班交流展示)
通过学生们的热情参与和积极思考,分别从“作相等证平行”和“作平行证相等”的角度总结出了两种不同的证明方法,证实了猜想.
师生共同揭示定理:(三角形中位线的性质)三角形的中位线平行于第三边,且等于第三边的一半.
三角形的中位线性质在几何问题中的用途较为广泛,所以在新授课时教师应关注学生对定理的理解程度,而定理的证明是能帮助学生理解它的由来及实质的,所以这个环节教师尽量放手,让学生自己探究,自己猜想,自己证明.
3. 活学活用,联系生活
定理内容的掌握是第一步,定理的运用才是学习定理的真正目的. 例题是数学新授课中不可或缺的教学资源,在教学中,尽量让例题贴近生活,让学生感受到数学与生活的关系,有利于学生提高对数学的兴趣,增强其学好数学的信心.
学材二(初显身手):如图4,△ABC中,D,E,F分别是AB,BC,AC的中点.
①若DF=5,则BC=______;
②若∠B=50°,则∠ADF=______;
③若AB=8,则EF=______;
④若G,H分别是BD,BE的中点,求GH的长度.
学材三(学以致用):如图5,有一处不规则图形的池塘边上有A,B两点,小明想测量A,B两点间的距离,你有什么办法吗?你的依据是什么?
(完成方式:学生独立思考完成,再全班交流展示)
以上两个问题分别是三角形的中位线在几何图形中的运用及实际生活中的运用,问题难度不大,学生基本能够独立完成. 并且针对第二个问题能提出两种方案,分别是将AB作为三角形的一边和三角形的中位线来构造三角形,用中位线的性质解决.
4. 类比推理,知识迁移
类比思想是数学中的重要思想,即将新知识与已掌握的知识相联系,从彼此的联系中找到新问题的解决方法,是学习新知识的常用方法,也是解决数学问题的常用思想. 通过类比学会知识的迁移,对新知识的掌握有着促进作用.
学材四拓展延伸):如图6,点E,F,G,H分别是四边形ABCD四边形的中点,观察四边形EFGH,你能猜想它的形状并证明你的猜想吗?
(完成方式:教师用几何画板演示,變换四边形ABCD的形状,学生观察)
生1:四边形EFGH是平行四边形.
师(追问):你能证明出来吗?
生1:如图7,连接AC,通过三角形中位线的性质证明EF和HG均平行且等于AC的一半,利用平行的传递性和等量代换证出EF和HG平行且相等.
生2:也可以连接DB,方法一样.
生3:还可以同时连接AC和DB.
师:同学们真了不起,你们都具有发现的眼光,我们给图中的四边形EFGH一个特定的名字:中点四边形.
师生共同总结结论:中点四边形是平行四边形.
师:刚才我们在变换四边形ABCD的形状时出现了几种特殊的位置关系,大家是否有发现呢?
(学生迟疑)
教师PPT展示几种特殊的位置关系,如图8、图9、图10.
通过观察比较,师生共同总结中点四边形的形状和原四边形对角线的关系:
原四边形的对角线垂直,则中点四边形为矩形;
原四边形的对角线相等,则中点四边形为菱形;
原四边形的对角线既垂直又相等,则中点四边形为正方形.
题后反思:在刚才的探究过程中你是否发现了三角形中辅助线的作法和中点个数的关系?
生:一个中点→构造中线;两个中点→构造中位线.
在以往的中点四边形教学中,学生不容易主动想到连接对角线作辅助线的方法,需要教师充分引导,而在掌握了三角形的中位线性质以后学习中点四边形,可以给学生明确的探究思路,促进学生对中点四边形形状的理解,提高了课堂效率. 另一方面,学生主动探究出证明方法,从中体会到成就感,对学好数学增强了信心.
将“三角形的中位线”与“中点四边形”相结合,实际上是将两课时的内容合并为一课时,试教后效果良好,学生在学习过程中体悟了类比思想和知识的迁移,一节课完成了两节课的教学目标,达到了事半功倍的效果.
“学材再建构”是对学材的充分考虑,是对资源的最大利用,它实质上是因材施教的一种体现. 在教学中教师应该关注知识的整体性、完整性和学生的多样性、发展性. “学材再建构”不是一种模式,没有固定的程序,教师在实施时应该依据“让学生的效益最大化”的原则让教学更适合学生的发展.
