带几何缺陷拱顶罐球壳的稳定性分析

徐君臣 吴云龙 沈 鋆 米 杰

（惠生工程 （中国）有限公司）

0前言

顶板带肋拱顶罐具有造价低廉、制造简单等优点，在石油、化工等行业得到了广泛应用。单台储罐大型化具有降低投资、节省钢材和减少配管量等优点，是目前储罐的主要发展趋势。由于大部分储罐的设计压力较低，罐顶壁厚较薄，再加上中间无支撑结构，故一般罐顶的稳定性较差。造成拱顶罐罐顶局部凹陷的原因主要有以下几方面： （1）施工过程中的不当操作； （2）使用过程中天气突然变化，使得储罐内蒸汽温度和压力急剧降低，呼吸阀出现堵塞，从而使储罐内形成较大的负压[1]；（3）罐顶出现不同程度的腐蚀减薄和裂纹缺陷；（4）暴风雨和暴风雪袭击等。若不对这些局部凹陷进行科学的评估和有效的修复，不仅可能造成设备失效，还可能引发灾难性的事故。因此，对带凹陷罐顶进行稳定性分析，对于储罐的安全使用和有效修复具有重要的意义。

带肋球壳拱顶罐一般按照 GB 50341—2014《立式圆筒形钢制焊接油罐设计规范》[2]进行设计，规范中附录H给出了带肋球壳拱顶许用外载荷的计算公式。该公式根据建筑科学院的研究成果，并考虑了钢球壳的特点、调整了系数而得到，而且还采用实际的储罐数据对该公式进行了相应的验证。随着计算机技术的快速发展，采用有限元方法对大型储罐进行稳定性分析得到了越来越多的关注。尹晔昕等[3]采用有限元方法对储罐拱顶进行了内压强度、稳定性以及外压稳定性计算，为工程设计提供了理论依据。黄文霞等[4]使用ANSYS软件建立拱顶罐力学模型，进行了失稳校核和内压强度分析，得出了储罐失稳的临界载荷。以上文献均将肋板折算成等效的球壳厚度，这势必会对计算结果产生影响。丁利伟[5]采用有限元软件对不同规格的扇形+葵花混合型和子午线型网壳进行了稳定性分析，计算结果表明扇形+葵花形网壳承载能力更强。刘江华等[6]采用有限元方法对局部均匀减薄拱顶进行了稳定性分析，并提出了一种近似的解析分析法，有限元方法计算的结果与解析法具有一致的计算精度。徐蕾等[7]对带体积缺陷的拱顶区域进行了均匀减薄处理，对缺陷发生的区域及拱顶的稳定性进行了大量的有限元计算，提出了相应的实用计算公式，为含缺陷加筋拱顶的安全评定提供了一定参考。基于以上研究，本文将根据现场实测的罐顶凹陷尺寸，建立带缺陷的加筋拱顶外压稳定性分析的有限元模型，得出含几何缺陷带肋拱顶的临界失稳载荷。同时，研究了罐顶不同结构尺寸对其承载外载荷能力的影响，为实际工程中拱顶罐的设计、安全使用以及现场有效修复提供理论基础。

1 储罐的几何尺寸与有限元建模

本文以10 000 m3带肋球壳拱顶罐为计算模型，其结构尺寸如图1所示。储罐内径为30 m，球壳半径为36 m，球壳厚度为8 mm，环向和径向加强筋均采用85 mm×10 mm的扁钢，球壳边缘与罐壁连接处采用L90×90×10角钢包边。在球壳上出现了直径为6 m的凹陷，凹陷最深达300 mm，凹陷边缘距筒体为1.5 m。该拱顶罐的设计外压为0.5 kPa，设计内压为1.5kPa，风载荷、雪载荷 （活载荷）折算成等效在球壳上的均布压力为1.0 kPa。罐体材料的弹性模量E为201 GPa，泊松比μ为0.3，抗拉强度为515 MPa，屈服强度为220 MPa。

图1 拱顶罐的结构

由于该结构的尺寸较大，若采用实体单元势必会造成较大的计算量。因此，分别采用了全壳单元、壳与梁组合单元进行有限元建模以减少计算量。本文采用Shell 181单元建立薄壳结构，该单元对大应变非线性问题有很好的处理能力；采用Beam 189单元建立梁结构，该单元每个节点同样具有6个自由度，能与Shell 181单元进行很好的耦合。由文献 [6-7]的模拟计算结果可知，罐壁及罐壁内的压力对罐顶失稳的临界载荷影响很小，几乎可以忽略。事实上，在包边角钢刚度足够大时，罐顶周边几乎相当于固支约束，是否建出罐壁对结构的临界载荷影响较小。通过模拟计算发现，模型中带罐壁与不带罐壁计算出的不带缺陷罐顶的一阶失稳临界载荷分别为5.62 kPa和5.57 kPa，两者之间相差较小，所以在建模时可不建出罐壁以减少计算量。在进行有限元建模时，罐顶和筋板都采用有效厚度进行计算。带缺陷拱顶罐有限元模型如图2所示。在进行网格划分时，采用4边形单元，不断对网格进行细化，直到求解的结果基本保持不变。建模时的边界条件为在加筋球壳的边缘施加全约束。

图2 带缺陷拱顶罐有限元模型

2 有限元模型验证

为了验证有限元程序的正确性，本文采用了半径为2.4～38 m的球壳作为验证模型。按照弹性稳定性理论，对于表面承受均匀外压的球壳，其承受的临界压力[8]为：

式中 pcr——临界压力，MPa；

E——弹性模量，MPa；

t——球壳厚度，mm；

R——球壳半径，mm。

从表1可以看出，有限元求解的临界载荷与经典小挠度解计算的临界载荷接近，相对误差均小于3%，证明了有限元模型的正确性。对于储罐内径为38m，球壳半径为38m，球壳厚度为5 mm的模型，文献[7]给出有限元计算的临界载荷为4.32kPa。

表1 不加筋球壳有限元结果与理论解对比

3 结果与讨论

3.1 不同建模方法对比

图3和图4分别为采用全壳单元、壳与梁组合单元在相同条件下的计算结果。从图3可以看出，采用全壳单元求出罐顶的一阶失稳临界载荷为5.57 kPa；从图4可以看出，采用壳与梁组合单元求出罐顶的一阶失稳临界载荷为5.96 kPa。全壳单元相对于壳与梁组合单元求解的相对误差为6.54%。一般来说，把球壳离散成壳单元、筋板离散成梁单元，更加接近工程实际情况。在对带缺陷加筋球壳进行有限元建模时也采用壳与梁组合单元。对于上面球壳半径为36 m不加筋的球壳，求出的一阶失稳临界载荷为4.75 kPa，加筋之后球壳的承载能力增加了25.47%。

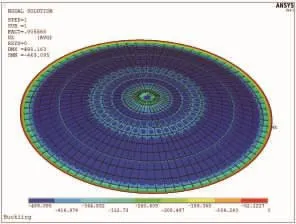
图3 全壳单元求解的临界载荷

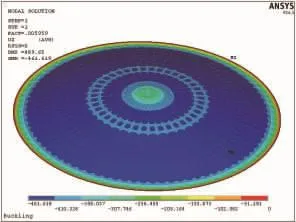
图4 壳与梁单元求解的临界载荷

3.2 带缺陷球壳稳定性计算

图5为采用壳与梁组合单元求解的带缺陷拱顶罐罐顶的结果。从图5中可以看出，带缺陷罐顶的一阶失稳临界载荷为3.94 kPa，相对于不带缺陷罐顶承载能力下降了33.89%。缺陷的产生对罐顶承载能力的削弱非常显著，影响储罐的安全使用，需要采用合适的方法对凹陷区域进行修复以恢复其承载能力。

3.3 在内压下球壳与带缺陷球壳的应力应变分析

在分析内压作用下球壳的应力应变时，为了考察球壳、包边角钢、筒体之间连接处的应力，在有限元建模时建出了包边角钢和部分罐壁。图6和图7分别为储罐在内压1.5 kPa作用下z方向的位移和等效应力分布云图。从图6和图7中可以看出，结构在z方向最大位移为13.23 mm，且方向垂直向上；其结构最大等效应力为136.59 MPa，且位于球壳与包边角钢连接处，主要是由于该处的结构不连续造成的。

图5 带缺陷球壳的临界载荷

图6 不带缺陷储罐位移分布云图

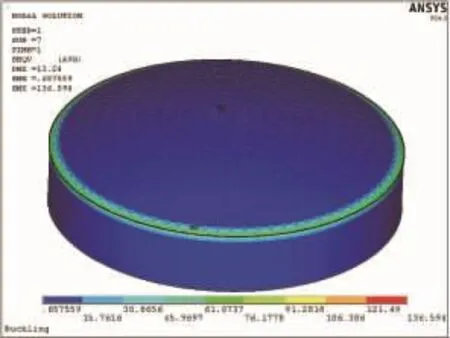
图7 不带缺陷储罐等效应力分布云图

图8和图9分别为带缺陷储罐在内压1.5 kPa作用下z方向的位移和等效应力分布云图。从图8和图 9中可以看出，结构在 z方向最大位移为26.77 mm，发生在带缺陷的区域，且方向垂直向上，这也说明了可以采用内部充气法使储罐凹陷的区域慢慢恢复至原来的形状。其结构最大等效应力为136.75 MPa，也发生在球壳与包边角钢连接处，与不带缺陷的储罐的最大等效应力接近。

图8 带缺陷储罐位移分布云图

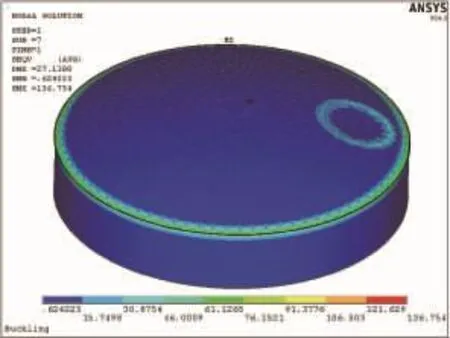
图9 带缺陷储罐等效应力分布云图

由以上分析可以看出，在内压作用下，罐顶凹陷区域产生垂直向上的位移，有利于储罐恢复原来形状，对结构的最大等效应力值影响较小，其值远小于材料的抗拉强度 （515 MPa）。但带凹陷的球壳在外压作用时，其承载外压的能力大大降低，需要对其进行现场修复来恢复其承载能力。

3.4 罐顶结构尺寸对其临界载荷影响

对于大型加筋拱顶罐而言，在不引起成本显著增加的情况下，如何有效增加其承载外载荷能力显得尤为重要。为了研究加筋球壳的结构尺寸对其承载外载荷能力的影响，本文分别以球壳有效厚度、筋板高度与筋板厚度、径向筋板数量为影响因素，找出对加筋球壳承载外载荷能力影响最显著的因素，以期为加筋球壳罐顶的设计提供一定的参考依据。表2列出了加筋球壳不同结构尺寸对其承载临界载荷的影响有关数据。

从表2中可以看出，增加筋板高度，结构临界载荷增加量与质量增加量的比值最大，达到90%左右； 增加球壳厚度， 增加量比值最小， 为11.90%。从表2中的增加量比值可以看出，对球壳临界载荷影响因素从大到小分别为：筋板高度、筋板厚度、径向筋板数量、球壳有效厚度。因此，在对加筋拱顶罐球壳厚度进行设计时，在外压载荷作用下球壳的厚度不需要取较大裕量，增加球壳厚度对其承受外压力影响较小，而且还会造成成本的显著增加。可以首先考虑增加筋板高度，其次是增加筋板厚度，最后是增加径向筋板数量，这些措施均可以不同程度地增加球壳承受外压力的能力，同时也可以降低储罐的制造成本。

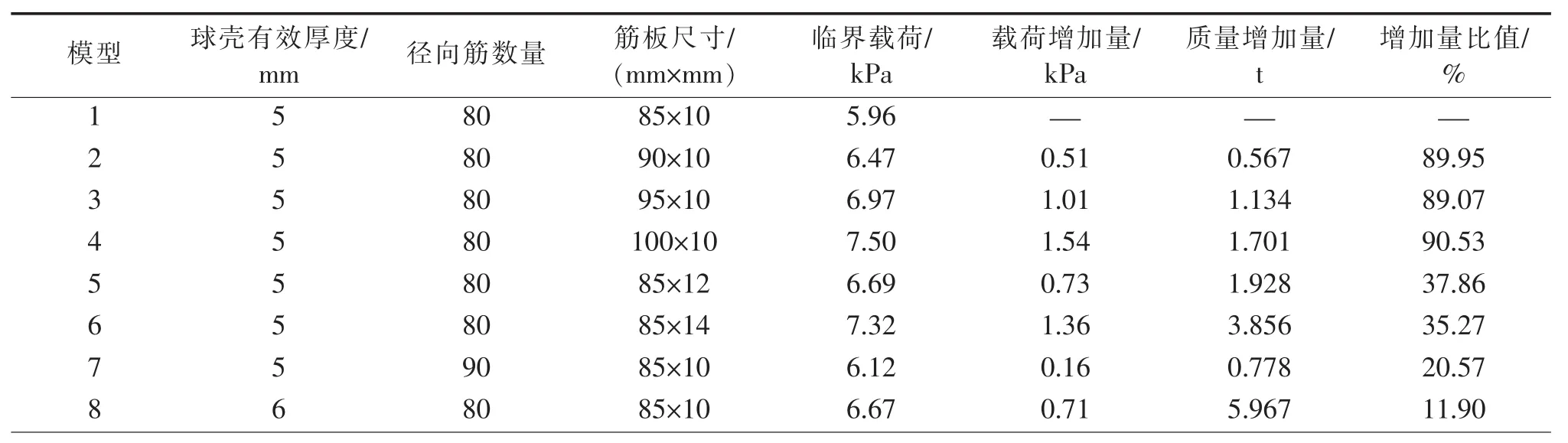
表2 不同结构尺寸模型对临界载荷的影响

增加筋板高度相对于增加筋板厚度对增加抗弯截面积影响更加显著，但对筋板的高厚比必须有所限定，否则在抗拱顶的失稳前筋板可能会侧向倾覆，起不到对拱顶的加强作用。图10给出了筋板高度与临界压力的关系曲线。筋板厚度固定为10 mm，不断调整筋板高度，当筋板高度为350 mm时，拱顶结构的临界压力达到最大值；随着筋板高度继续增加，拱顶结构的临界压力反而出现了显著下降。对于此模型，筋板的高宽比不能超过35，否则筋板对拱顶起不到加强作用；当筋板高度为160 mm时，临界载荷增加量与质量增加量的比值开始减小，即再增加筋板高度反而对增加拱顶承受临界外压的能力不利，而GB 50341—2014标准中也指出了筋板高厚比不宜大于12。

图10 筋板高度与临界压力的关系

4 小结

（1）基于ANSYS软件中的APDL语言编写了带缺陷与不带缺陷拱顶罐的有限元计算模型，获得了结构的一阶失稳临界载荷和在内压作用下的应力应变，为该结构的安全使用和现场修复提供了一定的理论基础。

（2）在对结构进行稳定性分析时发现，带凹陷储罐承载外压的能力下降了33.89%。由结构的内压分析可知，计算的最大等效应力值接近，合适的内压有利于修复储罐的凹陷区域。

（3）通过研究不同结构尺寸对加筋拱顶罐球壳承载外载荷能力的影响发现，在增加相同质量下，对加筋球壳承受外压力能力的影响从大到小依次为：筋板高度、筋板厚度、径向筋板数量、球壳有效厚度。当筋板的高厚比大于35时，拱顶承受外压的能力显著下降，这是因为在抗拱顶的失稳前筋板可能会侧向倾覆，起不到对拱顶的加强作用。

[1] 崔永超.2 000 m3拱顶罐凹瘪失效分析[J].化工装备技术，2011，32（3）：15-17，20.

[2] 立式圆筒形钢制焊接油罐设计规范：GB 50341—2014 [S].北京：中国计划出版社，2015.

[3] 尹晔昕，王瑜.大型拱顶储罐的有限元计算 [J].油气储运，2003，22（1）：23-26.

[4] 黄文霞，黄大伟，王永勇.渣油拱顶罐拱顶失稳的有限元分析[J].化工机械，2007，34（4）：193-196.

[5] 丁利伟.大型储罐罐顶网壳的稳定性分析比较 [J].石油化工设备技术，2011，32（3）：39-43.

[6] 刘江华，杨智春，李斌，等.局部减薄储罐拱顶非线性稳定性分析[J].机械强度，2009，31（1）：68-72.

[7] 徐蕾，崔立富，杜篷娟，等.含体积型缺陷加筋球壳拱顶的稳定性分析[J].自然灾害学报，2012，21（4）：216-222.

[8] 王志文，蔡仁良.化工容器设计[M].3版.北京：化学工业出版社，2005.