一种新的变步长LMS算法及分析

2018-01-17，

浙江工业大学学报 2018年1期

，

(浙江工业大学信息工程学院，浙江杭州 310023)

随着技术的发展，人们的生活水平不断提高，人们对于通信设备的使用需求大大增加，需求增加的同时人们对通信服务质量的要求也在不断提高，其中就包括噪声消除.自适应滤波技术[1-2]作为当前主流的噪声消除模块被大量应用于通信、雷达和车载系统等众多领域，其理论模型最早于1960年由Widrow和Hoff提出.它作为信号处理方向的具体应用分支，能够根据系统环境和噪声特点自适应地改进滤波器的滤波参数，使得滤波器能够动态地调整输入信号，提取有用信号，达到最佳滤波的效果[3].Kwong等[4]提到的经典LMS算法计算简便，但是算法中的固定步长无法满足收敛速度和稳态误差之间的矛盾；曾召华等[5]提到的NLMS算法虽然克服了LMS算法中固定步长产生的收敛速度和稳态误差之间的矛盾，但是其步长受到了信号噪声的影响；覃景繁等[6]提出了一种基于Sigmoid函数的变步长LMS算法，该算法能获得较快的收敛速度，较小的稳态误差，但是算法较复杂，计算量大，且在误差接近于0时会有较大的步长调整，不利于算法稳定；杨逸等[7]提出了一种指数因子变步长算法，该算法原理相似，同样能获得较快的收敛速度，但同样算法较复杂.

笔者主要针对语音通信系统环境，建立了一种新的步长和误差的非线性函数关系，提出了一种新的变步长LMS算法，算法简单易计算.此算法在收敛初期能够产生较大的步长，而在收敛稳态期能够产生较小的步长，符合算法的收敛原则.而且此算法在收敛稳态时具有较小的步长调整过程，克服了传统算法在收敛稳态期步长调整过大的缺陷，符合算法的稳定原理.同时也对新算法的参数进行仿真分析.

1 固定步长LMS算法

LMS算法是固定步长的线性自适应滤波算法[8]，它是依据有用信号和实际输出信号的误差的均方值来协调步长，用其来改善滤波器参数，因其每次改变的步长为固定值μ，因此称为固定步长滤波算法.图1为语音通信系统中的自适应滤波器的原理框图.信号源发出的信号d(n)作为原始期望信号被传入滤波器中.由于现实因素影响，实际接收到的信号并不是单纯的有用信号，容易被待滤除信号v(n)干扰.因此，真正输入信号为待滤除信号和有用信号的叠加信号x(n).y(n)为经由滤波器滤波后的输出信号，e(n)为输出信号和期望信号的误差.

图1 自适应滤波器滤波框图Fig.1 Frame diagram of adaptive filter

将有用信号和待滤除信号叠加后的信号x(n)传入自适应滤波器，通过自适应滤波后输出的信号y(n)与原期望信号d(n)进行比较，得到误差信号e(n)，通过误差信号的反馈来修改自适应算法的滤波参数w(n)来逐渐地调整自适应滤波器的收敛.在理想情况下，自适应滤波后的输出信号会无限接近于原始期望信号，即e(n)均方值无限接近0，在此情况下，即认为完美滤波.

在通信系统中，假定图1中的自适应滤波器为FIR滤波器[9-10]，而信号输入端的原始信号输入矢量X(n)和自适应参数W(n)分别设置为

X(n)=[x(n),x(n-1),…,x(n-m+1)]T
W(n)=[w0(n),w1(n),…,wm-1(n)]T

其中：m为滤波器阶数；n为当前取样点.

LMS算法的主要步骤如下：

1) 对算法进行初始化，即

W(n)=0

2) 对实际输入信号x(n)进行滤波，得到输出信号y(n)，即

3) 通过比较期望信号和输出信号来得到误差信号，即

e(n)=d(n)-y(n)

4) 由得到的误差信号来调整W(n)，即

W(n+1)=W(n)+2μX(n)e(n)

反复不断地重复步骤2)～4)直到误差e(n)趋于0且稳定.式中：μ为步长因子，为固定常数值，它的收敛范围为0<μ<1/λmax,λmax为输入信号方差矩阵的最大特征值.μ主要是用来控制算法的收敛速度和稳态误差，如果μ过小，则算法收敛慢但是稳定；如果μ过大，则算法收敛速度很快但是不稳定.因此，固定步长自适应滤波算法虽然简单易实现，但是它存在收敛速度和稳定性上的矛盾，需要通过一种变步长的自适应滤波算法来克服这种矛盾.

2 一种新的变步长LMS算法

根据覃景繁等[11]提出的步长调整原理，合格的变步长算法应能在算法收敛初期产生较大的步长来得到较快的收敛速度，从而能够更快地得到期望信号.而在收敛稳态期，这时算法的权值量已经非常接近最优值了，需要算法能够保持较小的步长来保持稳态，防止产生较大的误差，从而达到较小的稳态误差.当前的变步长LMS算法虽然能够满足步长调整原理，但是大多算法无法在收敛稳态期保证步长的缓慢变化，常常会有稳态期较小的误差变化而导致步长的极大变化，从而造成一系列连锁的较大误差，不利于算法稳定性.覃景繁等[6]提到的算法虽然拥有较快的收敛速度，但是在低误差的情况下拥有较大的步长变化度，不利于稳定性.因此，笔者提出了一种新的变步长算法，建立了一种新的步长和误差的非线性关系.此算法完全满足上述的步长变化原则，计算简便，复杂度低.而且新算法能够使步长在收敛稳态期不会产生较大的变化，防止偶尔误差的变化导致步长的极大变化，增大算法的适应性，有利于算法稳定性.新的步长因子为

因此，新的迭代公式为

式中：α为参数，主要是用来控制步长的变化范围；β为参数，主要是控制步长变化函数的变化陡峭程度.

步长μ和误差e(n)的关系如图2，3所示.当在收敛初级误差较大时，能对应有较大的步长来得到较快的收敛速度；而在收敛稳态期误差较小时，能对应有较小的步长来得到缓慢的收敛速度，符合算法的收敛原理.从图2，3中可以看出：算法在收敛稳态期误差趋于0时的步长变化梯度比较平缓，能够使算法由于偶然的误差激荡造成的步长变化不会那么大，符合算法的稳定原理.因为只有当μ满足0<μ<1/λmax时，算法才会收敛，所以α和β必须要保证使μ符合要求.而并不是所有满足条件的α和β都能使算法在收敛初期使步长较大，收敛稳态期使步长变小.如图2所示，假如收敛初期的误差为0.5，则α=0.2，β=1.5和α=0.2，β=2的2组能够在初期较快的收敛，而α=0.2，β=4的那组由于在初期没有获得较大的步长，无法获得较好的收敛效果.在满足算法收敛的前提下，β需要尽可能的小.而如图3所示，假如收敛初期的误差为0.6，则α=0.8，β=1.5那组能够在初期较快的收敛，而α=0.2，β=1.5的那组无法获得较好的收敛效果.在满足算法收敛的前提下，α需要尽可能的大.

图2 不同β参数下误差和步长关系的曲线图Fig.2 Graph of the relationship of error and step size in different β

图3 不同α参数下误差和步长关系的曲线图Fig.3 Graph of the relationship of error and step size in different α

在β相同的情况下，选择较大的α能获得较快收敛速度的同时也会产生较大的稳态误差.对参数α的取定要根据实际的应用环境，对收敛速度有较高要求的话，可以选择较大的α值；对稳态误差有较高要求的话，则应该选择合适的α值.

3 算法仿真

为了分析给出的变步长LMS算法的收敛能力以及α和β对算法收敛性能的影响，通过Matlab仿真工具[12]来对新算法的稳态误差和收敛速度等方面进行仿真分析.选择原始期望信号d(n)=sin(2πn/10)，待滤除信号是均值为0，信噪比为20 dB的加性白噪声，滤波器阶数为8.在进行100 次独立仿真实验后，取误差的平均值作为最后的稳态误差考量标准.

图4为α固定不变、β不同时的收敛曲线图.从图4中可以看出：随着β值的减小，算法的收敛速度逐渐提升，β不能小于1.如果β<1，则算法在稳态误差趋于0时会有较大的步长变化度，不符合步长变

化原理.在实验中，当β=1.1时，算法会出现不收敛的情况，因此实验的最佳β约为1.2.

图4 不同β参数的收敛曲线图Fig.4 The convergence curves of the different β

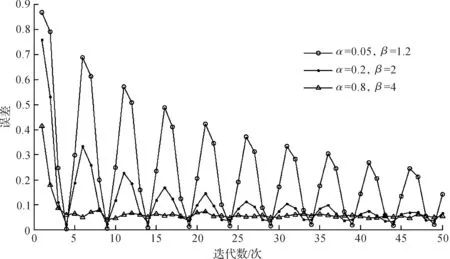
图5 不同α参数的收敛曲线图Fig.5 The convergence curves of the different α

图5为β固定不变、α不同的收敛曲线图.从图6中可以看出：随着α值的增大，算法的收敛速度逐渐提升，α不能大于1/λmax.如果大于1/λmax，则算法会发散.在实验的条件中，当α=0.9时，算法会发散，α为0.8～0.9时，有时会出现不收敛情况，因此实验的最佳α约为0.8.

图6 互不相同的2组α和β值的收敛曲线比较图Fig.6 The comparison of convergence curves of the different α and different β

图6给出的为2组不同的参数α和β值的收敛比较图，从图中看出α=0.2，β=4的收敛曲线由于参数的设置导致收敛初期的步长较小导致收敛速度过慢，而α=0.8，β=1.2的收敛曲线由于参数设置使算法能在收敛初期得到一个合适的步长来完成快速收敛，满足变步长步长调整原则，使算法有较好的收敛性能，与上述的理论分析一致.

刘剑锋等[13]提出了一种基于Lorentzian函数的变步长LMS算法，该算法通过Lorentzian函数来关联误差和步长.卢炳乾等[14]提出了一种基于正弦函数的变步长LMS算法，该算法通过正弦函数来构造了误差和步长的非线性关系.罗小东等[15]提出了一种基于Sigmoid函数的变步长LMS算法，该算法通过Sigmoid函数来构造误差和步长的函数关系.图7是新算法与3种已有变步长LMS算法在不同信噪比下的收敛比较图.采用本文献中的条件，主输入端输入信号为d(n)=sin(2πn/10)，加性干扰信号为白噪声，滤波器阶数为8，采用各自参考文献中的最佳参数值.其中基于Lorentzian函数的变步长LMS算法的算法参数设置为：α=0.05，δ=0.01；基于正弦函数的变步长LMS算法的算法参数设置为：α=10，β=0.04；基于Sigmoid函数的变步长LMS算法的算法参数设置为α=300，β=0.2.仿真100次求平均误差统计出曲线图.

图7中仿真结果显示：新算法在不同的信噪比下，均比其他3种算法拥有更好的收敛性能，因此新算法在自适应滤波上具有更好的适用性.

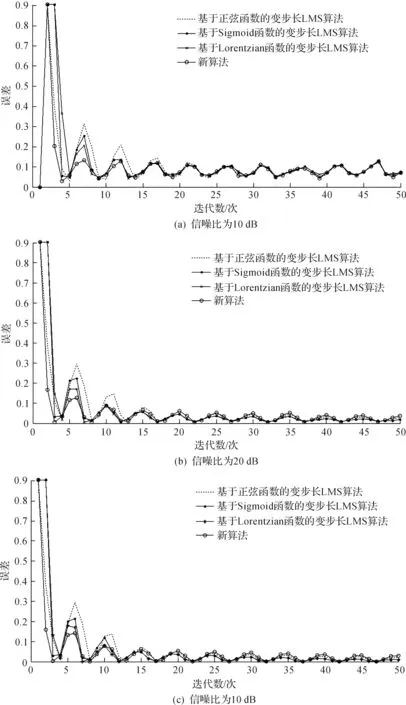
图7 新算法与3种变步长LMS算法在不同信噪比下的收敛比较图Fig.7 The convergence curves of proposed algorithm and three existing variable step size LMS algorithm in different SNR

针对语音通信的情况下，通过将仿真环境中的正弦波替换成语音信号来验证新算法的优劣性.同样采用图7中的算法参数，滤波器阶数为32，噪声信号为信噪比为20 dB的白噪声，采样频率为8 kHz.图8为语音信号和带噪信号的波形图，图9展示了各算法滤波后的语音波形.仿真结果显示，新算法相对于其他算法具有较好的滤波能力，在语音信号处理上具有一定的适用性.

图8 语音信号与带噪信号波形图Fig.8 The waveform of speech signal and noise signal

图9 基于各函数的变步长LMS算法滤波后的信号波形Fig.9 The waveform after filtering by the variable step-size LMS algorithms base on different functions

4 结论

研究了传统的固定步长LMS算法的优缺点，针对其缺陷和现在变步长算法步长调整原理，提出了一种新的变步长LMS算法.新算法通过建立一种新的步长和误差之间的非线性函数关系来实现步长的变化，并同时对新算法的各个参数进行分析.该算法有在收敛初期产生较大的步长同时在稳态期产生较小的步长来缓解稳态误差的特点.同时，该算法克服了传统算法在收敛稳态期步长变化过快的不足.理论分析和实验仿真都验证了该算法相对于已有算法都具有较好的收敛特性.下一步需要对算法参数进行精度上的进一步提升，同时对算法的限制性进行进一步的研究.

[1] HUANG B, XIAO Y, MA Y, et al. A simplified variable step-size LMS algorithm for Fourier analysis and its statistical properties[J]. Signal processing,2015,117:69-81.

[2] LU J, QIU X, ZOU H. A modified frequency-domain block LMS algorithm with guaranteed optimal steady-state performance[J]. Signal processing,2014,104(6):27-32.

[3] 孙明轩,余林江.离散时变系统的自适应迭代学习控制[J].浙江工业大学学报,2013,41(1):84-90.

[4] KWONG R H, JOHNSTON E W. A variable step size LMS algorithm[J]. IEEE transactions on signal processing,1992,40(7):1633-1642.

[5] 曾召华,刘贵忠,赵建平.LMS和归一化LMS算法收敛门限与步长的确定[J].电子与信息学报,2003,25(11):1469-1474.

[6] 覃景繁,韦岗.基于S型函数的变步长LMS自适应滤波算法[J].无线电工程,1996(4):44-47.

[7] 杨逸,曹祥玉,杨群.基于指数函数的归一化变步长LMS算法[J].计算机工程,2012,38(10):134-136.

[8] SIMON H.自适应滤波器原理[M].郑宝玉,译.4版.北京:电子工业出版社,2010.

[9] 金燕,王明,葛远香.基于FPGA的抗混叠FIR数字滤波器的设计与实现[J].浙江工业大学学报,2010,38(2):192-196.

[10] 赵旋,何德峰,周洲.网络控制系统多变量DMC算法的稳定性分析[J].浙江工业大学学报,2012,40(2):209-212.

[11] 覃景繁,欧阳景正.一种新的变步长LMS自适应滤波算法[J].数据采集与处理,1997(3):171-174.

[12] 李正周.MATLAB数字信号处理与应用[M].北京:清华大学出版社,2008.

[13] 刘剑锋,蒋卓勤,李娟,等.一种基于Lorentzian函数的变步长LMS自适应滤波算法[J].指挥控制与仿真,2009,31(2):42-44.

[14] 卢炳乾,冯存前,龙戈农.一种基于正弦函数的新变步长LMS算法[J].空军工程大学学报(自然科学版),2013,14(2):47-50.