随机时延网络化系统的模型预测控制

，

(浙江工业大学 信息工程学院，浙江 杭州 310023)

网络控制系统(Networked control systems, NCS)是近些年来控制领域研究的热点之一，其在机器人遥操作、智能家居和工业控制等领域都有着广泛的应用，并取得了巨大成功.但通过网络构建的控制系统，网络传输过程中几乎不可避免的存在时延问题[1].在控制系统设计过程中，如果忽视时延问题，将导致控制系统的性能下降，甚至无法稳定工作[2].针对NCS中的时延问题，近年来国内外众多学者提出了不少有效的处理方法，如随机最优控制方法、时滞系统方法、混杂系统方法和预测控制方法等[3-16].

在NCS中，时延的时变和随机特性，使得网络时延表现为采样周期的非整数倍.Zhang等[8-9]采用切换系统方法研究了时变时延问题.在设定的切换律下，将时变时延系统转换为确定性系统，但采用确定性方法补偿时变时延时具有很大的保守性.预测控制的多步预测和滚动优化方法能够一次计算未来多个控制量，在执行器无法得到最新的控制量时，可以利用已有数据包中的预测值进行控制.宋洪波等[10]通过一种改进的分布式预测补偿方式，利用反馈数据来提高系统的控制性能.葛阳等[11-12]通过利用动态矩阵控制(DMC)算法在网络传输中的控制量和未来预测值的冗余信息来代替丢失的数据，减少时延和丢包对系统性能的影响，改进了NCS下的DMC算法.Tang等[13-15]采用广义预测控制(GPC)算法对网络时延和丢包问题进行了研究.控制器和执行器采用时间驱动方式，将非整数倍采样周期时延转化为采样周期的整数倍，但这种方法人为地增加了时延，从而导致性能的下降.然而，非整数倍采样周期时延是时变或随机的，采用确定性方法将带来很大的保守性.因此，针对非整数倍采样周期时延，研究能够补偿随机时延的网络化预测控制算法将更有意义.

1 NCS建模

考虑如图1所示的NCS，其中的被控对象由以下的连续时间线性时不变系统模型描述

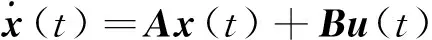
(1)

图1 网络控制系统的结构图Fig.1 The structure of NCS

图1所示的网络控制系统，满足以下假设：

1)传感器节点为时间驱动，以固定的采样周期T对被控对象采样，控制器节点采用事件驱动.

2)执行器节点采用时间驱动，但是以更高的频率读取缓冲区，读取周期为T0=T/N，N为一个正整数，为可调参数.

3)不存在数据包丢失，且数据包均带有时间戳.

πrs=Prob{d(k+1)=s|d(k)=r}

由于时延小于一个采样周期，在[kT,(k+1)T)内，有两个控制信号u(k-l),l=0,1被作用.假定控制信号u(k-l)的作用时间为nl(k)T0，有n0(k)+n1(k)=N.所考虑的NCS可建模为离散时间线性系统[8]，即

(2)

在[kT,(k+1)T)内，令n(k)=[n0(k)n1(k)]，控制信号的值取决于nl(k),l=0,1，子系统式(2)动态的由n(k)决定.为了描述相应的子系统，在这引入映射关系ψ:d(k)→σ(k)，即

(3)

式中：n(k)∈{[N0],[N-1 1],…,[0N]}，σ(k)∈{0,1,…,N}.则式(2)可描述为

(4)

其中Hiσ(k)=Hi(d(k)).

记XT(k)=[xT(k)uT(k-1)]，则式(4)可描述为

(5)

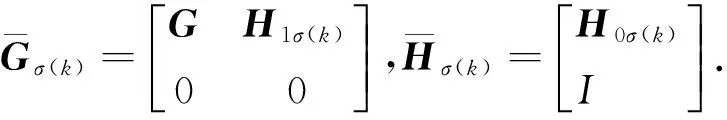
考虑到实际控制对象中的输入约束的存在，对式(5)增加了对控制输入约束的考虑，即

(6)

针对具有时延的NCS，设计一个模式依赖的稳定化状态反馈控制律

u(k+i|k)=Kσ(k|k)X(k+i|k)

(7)

使得无限时域预测控制性能指标在线最小化，即

(8)

i|k)Ru(k+i|k)]|Mk}

(9)

式中：Kσ(k|k)为状态反馈控制器增益；Q，R分别为给定的对称正定加权矩阵；X(k)=X(k|k)为采样时刻k的状态测量值；X(k+i|k)为k时刻对k+i时刻的状态预测值；u(k+i|k)为k时刻满足式(8)的受控输入序列在k+i时刻的值；E{·}为数学期望；Mk={x(0),d(0),…,x(k),d(k)}.则闭环系统可描述为

X(k+i|k)

(10)

注2：式(10)的状态空间系数矩阵由当前模式决定.在k时刻已知时延模式d(k)，可得n(k)和σ(k)，则状态反馈增益Kσ(k)=Kd(k).

定义1对于任意的初始条件{X(0),d(0)}，如果不等式

(11)

成立，则式(10)是随机稳定的.

2 稳定性分析与控制器设计

以下定理给出了保证式(10)随机稳定的状态反馈控制器存在的条件和设计方法.

定理1考虑式(9，10)，若最小化问题

(12)

(13)

(14)

(15)

证明定义Lyapunov函数

V(X(k+i|k),σ(k+i|k))=

XT(k+i|k)Pσ(k+i|k)X(k+i|k)

(16)

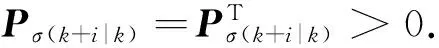
令σ(k+i|k)=r,σ(k+i+1|k)=s.假设在采样时刻k，对于所有的X(k+i|k)和u(k+i|k)，i≥0，满足以下不等式

E{V(X(k+i+1|k),s)-V(X(k+i|k),r)|Mk}≤

(17)

为保证J(k)有界，令E{V(X(∞|k),σ(∞|k))|Mk}=0.将式(17)两边从i=0到i=∞求和可得

J(k)≤V(X(k|k),σ(k|k))

(18)

因此，式(9)存在上界.式(10)的优化问题则等价于最小化V(X(k|k),σ(k|k))，即

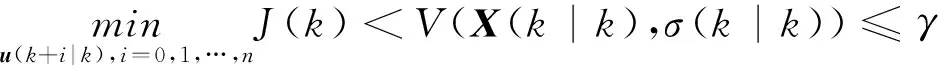
(19)

则根据式(19)可得

XT(k|k)γ-1PrX(k|k)≤1

(20)

由式(17)可得

(21)

由Schur补引理可得式(21)等价于以下不等式

(22)

在采样时刻k，考虑式(6).由于XT(k|k)γ-1PrX(k|k)≤1是式(10)的不变椭圆集合[19]，所以有

(23)

由S-procedure和Schur补引理可得

(24)

对式(24)分别左乘和右乘矩阵diag{I,Yr}，则可知式(24)等价于式(15).证毕.

定理2在任意时刻k≥0，如果优化问题式(12～15)具有可行解，则式(10)表示的闭环系统是随机稳定的，且存在式(7)所示的状态反馈控制律.

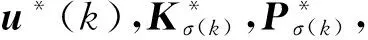
E{V(X(k+i+1|k),σ(k+i+1|k))-

V(X(k+i|k),σ(k+i|k))|Mk}≤0

(25)

由式(19，25)可得

E{V(X(k+i|k),σ(k+i|k))|Mk}≤

E{V(X(k|k),σ(k|k))|Mk}≤γ

(26)

对于所有σ(k+i|k)∈N，由式(10)可知X(k+1|k)=X(k+1|k+1)，则可得

E{V(X(k+1|k+1),σ(k+1))|Mk+1}≤
E{V(X(k+1|k+1),σ(k+1|k))|Mk+1}=
E{E{V(X(k+1|k),σ(k+1|k))|Mk}|Mk+1}≤γ

(27)

所以式(13)在k+1时刻也是可行的.由式(14，15)与状态向量X(k|k)无关且u(k+1|k+1)=u*(k+1|k)可知，式(14，15)在k时刻的最优解在k+1时刻是可行的，因此式(12～15)在任意时刻k≥0都是可行的.由最优原理可得

E{V(X(k+1|k+1),σ(k+1|k+1))|Mk+1}≤

E{V(X(k+1|k+1),σ(k+1|k))|Mk}

(28)

由式(17)可得

E{V(X(k+1|k),σ(k+1|k))-V(X(k|k),

σ(k|k))|Mk}≤-E{XT(k|k)QX(k|k))|Mk}

(29)

由于状态X(k+1|k+1)=X(k+1)，结合式(28，29)可得

E{V(X(k+1|k+1),σ(k+1))-V(X(k|k),σ(k))·

|Mk}≤-E{XT(k|k)QX(k|k))|Mk}≤

-λE{‖X(k|k)‖2|Mk}

(30)

式中λ为正定矩阵Q的最小特征值.将式(17)两边从k=0到k=∞求和，可得

E{V(X(∞),σ(∞))-V(X(0),σ(0))|M0}≤

(31)

从而可得

σ(0))|M0}<∞

(32)

由定义1可知，闭环系统式(10)是随机稳定的.证毕.

3 仿真示例

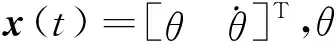
以此不稳定的倒立摆作为被控对象构成网络控制系统，取传感器的采样周期为T=0.3 s，N=3，则执行器端读取缓冲区的周期为T0=0.1 s，d(k)∈{0,1,2,3}.将被控对象离散化得

则选取一组时延模式d(k)的分布，如图2所示.

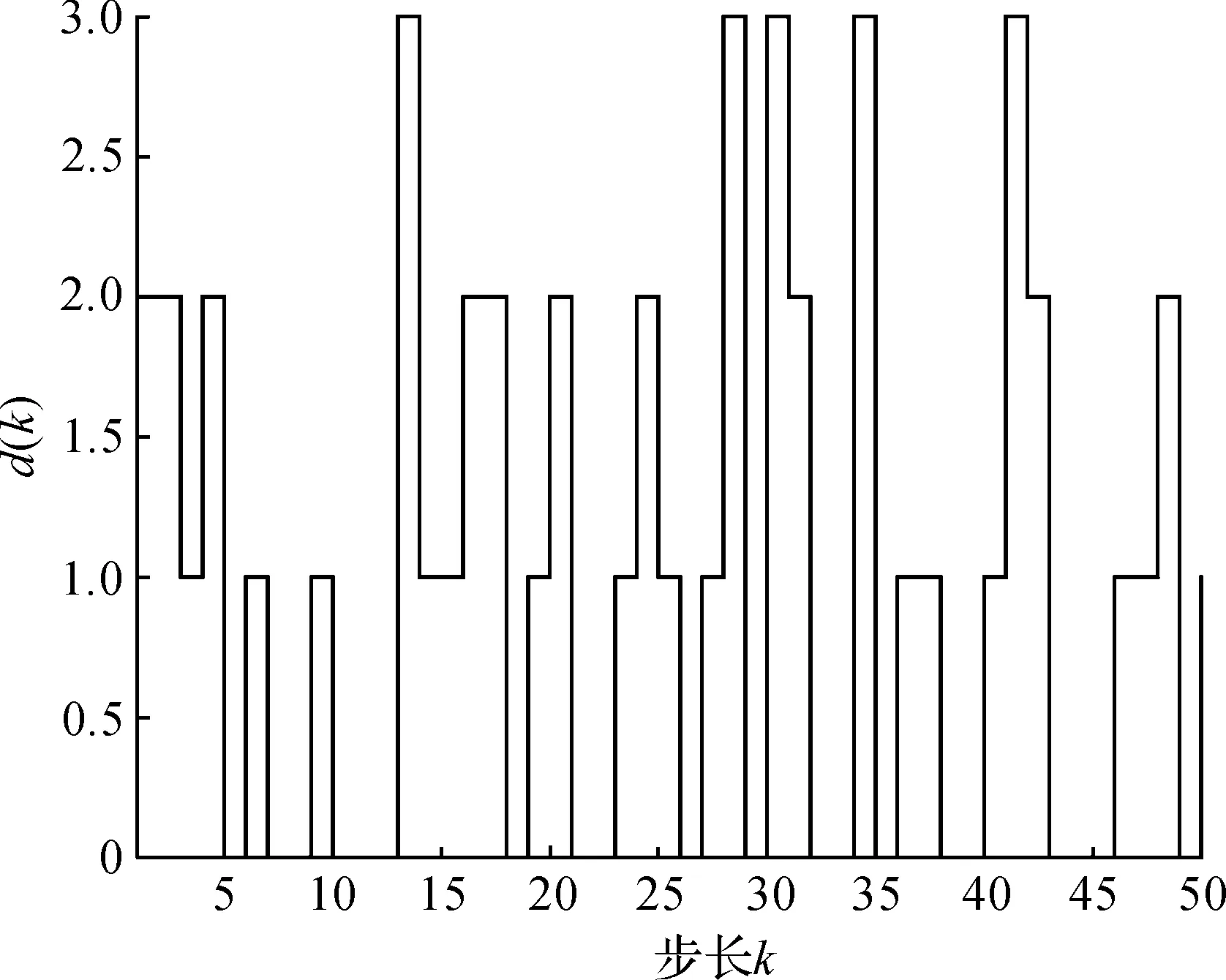
图2 时延模式d(k)Fig.2 Delay mode d(k)

根据以上所提的控制律计算方法，在k时刻在线求解优化问题式(12～15)，可求得每个采样时刻的状态反馈控制律u(k)，从而得到如图3所示的控制信号，由图3可知控制信号满足输入约束.在u(k)作用下闭环系统状态轨迹(图4)，仿真结果表明：在所设计的具有输入约束的状态反馈控制器的作用下，闭环NCS随机稳定.

图3 控制输入Fig.3 Control input

图4 状态轨迹Fig.4 State trajectory

4 结 论

针对非整数倍采样周期时延NCS，采用执行器读取缓冲区频率快于系统采样频率的工作模式，将NCS建模为一类马尔可夫跳变系统，然后运用模型预测控制滚动优化的思想，推导了系统随机稳定的充分条件，并运用线性矩阵不等式方法求解了状态反馈控制器.从仿真结果可以看出：针对时延小于一个采样周期的NCS，运用随机系统方法建模和模型预测控制方法设计控制器，可以实现系统稳定化状态反馈控制器的设计，并且控制输入满足输入约束.

[1] 周颖,樊春霞,杨富文,等.网络环境下的大系统鲁棒H∞控制[J].系统科学与数学,2011,31(6):709-719.

[2] 夏元清.云控制系统及其面临的挑战[J].自动化学报,2016,42(1):1-12.

[3] ZHANG L X, GAO H J, KAYNAX O. Network-induced constraints in networked control systems-a survey[J]. IEEE

transactions on industrial informatics,2013,9(1):403-416.

[4] HU S S, ZHU Q X. Stochastic optimal control and analysis of stability of networked control systems with long delay[J]. Automatica,2003,39(11):1877-1884.

[5] GAO H J, CHEN T W, LAM J. A new delay system approach to network-based control[J]. Automatica,2008,44(1):39-52.

[6] HU L S, BAI T, SHI P, et al. Sampled-data control of networked linear control systems[J]. Automatica,2007,43(5):903-911.

[7] ZHANG W, BRANICKY M S, PHILIPS S M. Stability of networked control systems[J]. IEEE control systems magazine,2001,21(1):84-99.

[8] ZHANG W A, YU L. New approach to stabilization of networked control systems with time-varying delays[J]. IET control theory and application,2008,2(12):1094-1104.

[9] LIN H, ANTSAKLIS P J. Stability and persistent disturbance attenuation properties for a class of networked control systems: switched system approach[J]. International journal of control,2005,78(18):1447-1458.

[10] 宋洪波,刘国平.具有多传输通道系统的网络化预测控制[J].控制理论与应用,2015,32(7):912-917.

[11] 葛阳,王景成.基于动态矩阵的随机时延丢包网络控制系统[J].信息与控制,2011,40(6):835-840.

[12] 葛阳,王景成.网络化系统中动态矩阵控制的稳定性条件[J].控制理论与应用,2012,29(7):949-954.

[13] TANG P L, DE SILVA C W. Compensation for transmission delays in an Ethernet-based control network using variable-horizon predictive control[J]. IEEE transactions on control systems technology,2006,14(4):707-718.

[14] LIU G P, MU J X, REES D, et al. Design and stability of networked control systems with random communication time delay using the modified MPC[J]. International journal of control,2006,79(4):288-297.

[15] LIU G P, CHAI S C, MU J X, et al. Networked predictive control of systems with random delay in signal transmission channels[J]. International journal of systems science,2008,39(11):1055-1064.

[16] 仇翔,滕游.离散时滞系统的网络化保成本控制[J].浙江工业大学学报,2014,42(4):443-448.

[17] 赵旋,何德峰,周洲.网络控制系统多变量DMC算法的稳定性分析[J].浙江工业大学学报,2012,40(2):209-212.

[18] 何德峰,周洲,郭海锋.网络化控制系统鲁棒动态矩阵控制[J].浙江工业大学学报,2013,41(1):91-95.

[19] KOTHARE M V, BALAKRISHNAN V, MORARI M. Robust constrained model predictive control using linear matrix inequalities[J]. Automatica,1996,32(10):1361-1379.

[20] LIU A, ZHANG W A, YU L, et al. New results on stabilization of networked control systems with packet disordering[J]. Automatica,2015,52:255-259.

[21] 于之训,陈辉堂,王月娟.基于Markov延迟特性的闭环网络控制系统研究[J].控制理论与应用,2002,19(2):263-267.