改进SIFT算法实现图像的快速匹配

吴丽君，文吉成，陈志聪，陈金伙，林培杰，程树英

(福州大学物理与信息工程学院，微纳器件与太阳能电池研究所，福建 福州 350116)

0 引言

图像特征匹配是实现图像搜索[1]、图像分类[2]、目标识别[3]、图像拼接的重要基础. 为提高匹配性能，通常借助局部特征提取算法，如SIFT[4]、SURF[5]、BRIEF[6]等来完成匹配. 与全局特征(如直方图等)相比，局部特征能更好地应对旋转、尺度等变化. SIFT因其良好的匹配性能[7-9]得到广泛的运用. 在此基础上，研究人员从各方面提出更具有适应性的算子(如PCA-SIFT[10]和AFFINE-SIFT[11])，进一步增强SIFT的鲁棒性和描述能力，以期获得更好的匹配性能. 然而, 改进算法在提高匹配性能的同时降低了匹配速度，其中，以AFFINE-SIFT算法尤为明显. 为了在保留匹配性能的同时不影响匹配速度，研究者提出了各种优化速度的SIFT算子[12-14]. 宋佳乾等[12]首先运用Canny算子去除边缘点，然后通过K-L变换降低描述子维度，这可以在提高速度的同时保持较高的正确匹配率，但是所剩的匹配点数量过少. 李丹等[14]提出采用24维特征描述符代替128维特征描述符，并引入最小优先队列和马氏距离，这在一定程度上提高了匹配速度，但最终获得的匹配数量仍然比较少. SAR-SIFT[13]采用一种新的梯度计算方法，并对SAR(synthetic aperture radar)图像中的斑点噪声具有鲁棒性, 但这限于分析SAR图像. 此外，基于FPGA[15]平台的并行加速算法也被提出，但这种算法需要消耗额外的计算资源，并没有从本质上降低算法所需的计算量.

众所周知，基于局部特征点的图像匹配流程可以分为特征点提取、描述符生成、粗匹配及误匹配剔除四个步骤. 基于OpenSIFT源代码，笔者对图像匹配中各个步骤所需的运行时间及有效特征点的比例进行了分析. 以图1中两幅图像的匹配为例，在 i33220t CPU@2.80 GHz, 4.0 GB RAM的PC机环境上运行的数据如下：两幅图提取特征点的时间为10.469 s，所提取的总特征点数为(11 221，10 835)，特征点匹配过程中，描述子计算耗时19.04 s，粗匹配提取耗时4.36 s, 误匹配剔除耗时6.73 s，所得的匹配特征点数为(411，411)，误匹配特征点数为(10 810，10 424)，最终匹配率为(3.66%，3.79%). 由此可得后半阶段时间占了74%(30.13 s: 40.59 s). 对所提取的大量特征点生成描述符的过程耗费大量的时间，而这些特征点中有极大部分的特征点是无效特征点，即无法被匹配. 对大量无效特征点的描述大大降低了SIFT算法的运行效率. 基于此，提出通过特征点邻域灰度值的熵分布特性来筛除部分无效特征点，从而达到提速的效果. 为进一步降低算法所需的时间，还在误匹配剔除算法上进行了一定的优化：首先根据先验知识对匹配样本进行排序，之后采用双模型互校验的方式计算得到正确模型. 通过与文[12]和文[14]算法的比较表明，上述改进的图像匹配方案在基本保持原有方案(SIFT与RANSAC相结合的方案)性能的基础上，大幅提高特征点匹配的实时性、匹配率及正确匹配率.

图1 实际拍摄的待匹配图像Fig.1 Images needed to be matched

1 特征筛选算法框架

1.1 过滤不稳定的特征点

在SIFT算法中，通过DoG(difference of gaussian)检测特征点的过程中会保留较强的边缘效果. 尽管后续通过Hessian矩阵能够排除部分不稳定点，但是仍然有大量的无效特征点无法被移出. 在如图1所示的例子中，所剩不稳定特征点数量仍然很多，这导致特征点的有效匹配率低.

通过对特征点匹配与否进行研究可得, 一个特征点是否能够得到匹配主要依赖于以下两方面. ① 当前特征点在对应的图像中存在相应的匹配点. 由于视角不同，有的特征点已经不在对应图像的视场范围中，因此也无法找到特征点. ② 特征点是否包含足够的信息量以区别于其他特征点. 一个特征点如果包含足够大的信息量，则可视为是一个稳定特征点. 本研究着重讨论如何根据第二方面所提到的特征点的稳定性来提高有效匹配的比例.

不同检测算法所获取的特征点虽然会有一定差异，但所有检测到的特征点邻域范围内都会有一定的灰度变化. 根据信息论原理，特征点邻域灰度值变化越剧烈，其携带的信息熵越大，即能提供越多的信息用于特征匹配. 图2显示了三种情况: ① 包含一个稳定的特征点，其邻域灰度变化较为明显; ② 包含了不稳定特征点，其邻域变化情况次明显; ③ 不包含特征点，其邻域灰度值变化不明显. 据此，可以通过特征点邻域熵的大小筛选出稳定的特征点. 然而，图像匹配中，不同图像尺度不同，在一个固定大小的邻域上统计熵不合理. 本研究提出，通过计算特征点两个不同大小邻域内的差熵(根据实验经验，将两个邻域大小分别取为7×7和19×19)，以判断其稳定与否.

图2 特征点的三种情况Fig.2 Neighborhood of different types of feature points

首先用SIFT算法来匹配如图3所示的两张图片，并对此过程进行分析. SIFT分别从图3(a)、图3(b)中提取了1 021和638个特征点(在图中以蓝色标记)，最终共得到78对匹配. 经过RANSAC筛选后可得，其中正确匹配的有67对. 在此过程中，特征点的匹配率仅为7.6%(图3(a))和12%(图3(b))，其余92.3%和88%的特征点虽然最终没有匹配，但作为候选匹配特征点，其描述符也必须被计算，因此降低了算法的效率. 本算法旨在计算特征点描述符之前，先基于其邻域的差熵来筛选特征点，以去除部分不稳定匹配特征点，减少对不稳定特征点计算描述符所需的时间. 通过计算图3(a)、图3(b)中特征点邻域的差熵，并将据此筛选出的不稳定特征点(标记为红色，478个和380个)，如图3所示. 据测试可得未标记点中共有61对匹配，且全部为正确匹配，即匹配率提高为11.5%和23.6%. 由此可以判定，本算法可以成功地筛除部分不稳定特征点.

1.2 算法实现步骤

图4 熵特征筛选算法流程图Fig.4 Flow-chart of entropy-based feature point filter algorithm

熵特征筛选算法流程图见图4. 具体算法步骤如下：设X={x1,x2,x3,x4, …,xn}为SIFT算法提取到的特征点，n为特征点的个数，Ixi为图像灰度值.

Step 1 统计当前设定邻域中像素灰度出现的概率；

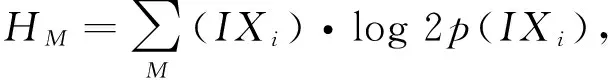
Step 3 同样地计算N×N邻域熵HN；

Step 4 计算差熵；

Step 5 如果差熵小于阈值，则判为不稳点特征点，否则保留；

Step 6 得到稳定特征点.

2 去除错误匹配框架

图5 误匹配示例Fig.5 Illustration of mismatching

SIFT算法中，通过特征点的描述符向量之间的欧式距离来判断两幅图像中的任意两个特征点是否匹配. 具体地说，对某一个特征点，找到另一幅图像中与它欧氏距离最近的特征点及次近的特征点，如果两者的欧式距离的比值小于0.49，则认为是匹配的. 这个过程称为粗匹配，这会带来一定的误匹配，如图5所示，红色显示的部分显然为误匹配.

粗匹配后会存在误匹配，而正确匹配是图像匹配应用的基础. 因此学者们提出了相应的算法来筛选出正确匹配，如RANSAC(random sample consensus)算法[16]. RANSAC能取得较高的正确率，然而它需要迭代选取样本以找到最大一致样本集，所需计算时间与样本数量平方成正比，无法适用于大数量计算. RRANSAC算法[17]通过迭代来提高鲁棒性，使其适应更低的内点比例； Anders Hast提出Optimal RANSAC算法[18]，进一步降低内点比例到5%，却增加了计算时间. 为提高时间效率，PROSAC(progressive sample consensus)算法[19]按照先验知识进行排序，以减少迭代次数来实现快速计算，但当匹配数量过多时，运算时间仍较长. 为进一步优化算法来适应多匹配对条件下的快速计算，本研究提出对新模型的估计算法：首先根据先验知识对样本进行排序，同时选取两组随机样本以获得两个匹配模型； 当模型一致时，作为初始正确模型； 经过数次更新，最终得出正确模型.

基于匹配特征对的坐标信息，通过一组匹配点对即可求得一幅图像到另一幅图像之间的变换矩阵：

图6 误匹配剔除算法流程图Fig.6 Flow chart of mismatching elimination algorithm

如果选中的一组样本点都是正确匹配，那么他们之间的映射关系必然一致. 而根据SIFT算法匹配规则，最近邻与次近邻的比值越小，两者匹配的置信度越高. 因此，可以依据相似度比值对匹配集合降序排列，越靠前的匹配则拥有更高的正确匹配概率. 对排序后的匹配集合进行高斯采样，以更大的机率采样靠前的匹配. 然后基于任意两组特征点计算出两个映射矩阵. 如果这两个映射矩阵之间的距离小于某一阈值，那么将此作为初始测试模型，并可以根据这个模型去测试其他的特征点. 经过数次更新后，即可减少模型误差. 具体流程如图6所示.

算法实现步骤如下:

Step 1 对所有匹配成功的特征点依照其最近邻与次近邻比率进行降序排列.

Step 2 以高斯分布随机抽取8个特征点，并计算映射矩阵M1，M2.

Step 3 计算∑(|M1-M2|)，当结果小于阈值，则判断为正确模型，并测试其他点；

否则转入Step2.

Step 4 已达到最大迭代次数或者已无误匹配点可去除，则转到Step5； 否则，将得到的正确匹配集合当做新的特征点集合，转入Step2.

Step 5 输出匹配结果.

3 实验设计及结果分析

图像匹配算法的性能与速度对于图像匹配的重要性不言而喻. SIFT效果好但耗时，这不仅因为SIFT算法本身的复杂度高，也因为SIFT需要对大量的不稳定特征点进行描述及匹配. 如前所述，本方案引入了特征点筛选算法以筛除部分不稳定特征点，减少对其进行描述及匹配所需时间，并进一步在误匹配去除步骤上进行简化，提高误匹配去除效率. 在这一部分，将通过实验验证所提出的改进方案(包括特征点筛选和改进的误匹配拒绝算法)的性能. 采用1 224像素×1 636像素的复杂图像和已知单应矩阵的图片作为实验素材，分别基于传统方案、已有的改进方案及本改进方案实现图像匹配，并分别统计改进前后所需要的时间、匹配成功的点数、匹配正确的点数和总点数.

3.1 测试特征点筛选算法

首先使用SIFT算法提取图片特征点，然后通过本算法过滤掉无效特征点，在此基础上实现特征点描述符的计算及特征点匹配，最后使用本改进算法去除误匹配. 实验中涉及到算法的两个参数，计算差熵所需邻域大小以及阈值. 将计算差熵的邻域大小设置为经验值7×7以及19×19，阈值设置为平均值加上一个很小的偏移系数-0.03.

实验1对一幅1 224像素×1 636像素的复杂图像的匹配结果进行了测试，结果见图7. 图7(a)为未改进算法的匹配结果，图7(b)为使用本算法的匹配结果，可看到本算法成功保存了大量匹配点对.

图7 实验1的匹配结果Fig.7 Image matching result in experiment one

为进一步测试算法的有效性，实验2加入一些已知单应矩阵的不同场景下的图片对算法进行测试. 其中，BOX-SCENE图像对如图3所示，而BOAT、BARK、TREE、GRAF图像对如图8所示.

图8 BOAT、BARK、TREE、GRAF图像对Fig.8 Image sets of BOAT, BARK, TREE and GRAF

提取上述每对图像的特征点总数，匹配特征点数及正确匹配点数如表1所示. 由于同一对图像中两幅图像所提取的特征点数量不尽相同，所以表中用左图特征点数量和右图特征点数量的格式来表示. 图9则显示了原始算法及改进算法的匹配率(匹配的点数/左图特征点总数)、正确匹配率(正确匹配点数/匹配特征点数). 据表1和图9可知，在相同条件下，相比原始算法，改进算法筛除了大部分的特征点数量，而最终正确匹配点对的数量却变化不大. 针对不同类型的图片对，改进算法在匹配率上有了大幅提高，这说明改进算法在成功剔除一部分不稳定特征点的同时，保留了大部分正确匹配点数，能较好地保存稳定特征点对. 因此，本研究所提出的根据稳定性系数来剔除不稳定特征点的方法是行之有效的.

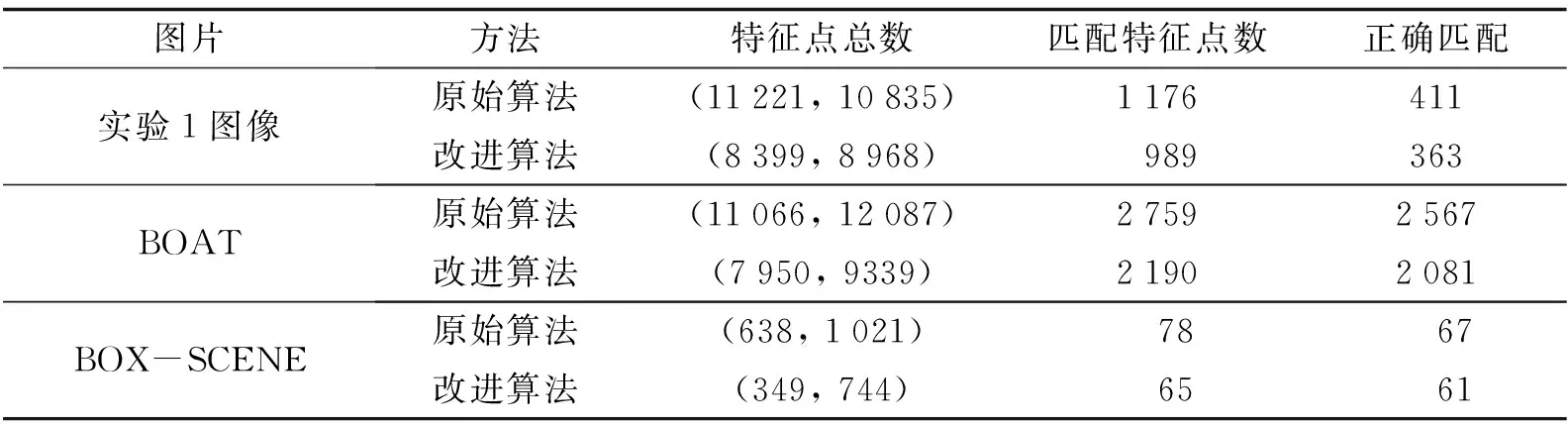
表1 实验2中特征点筛选的结果

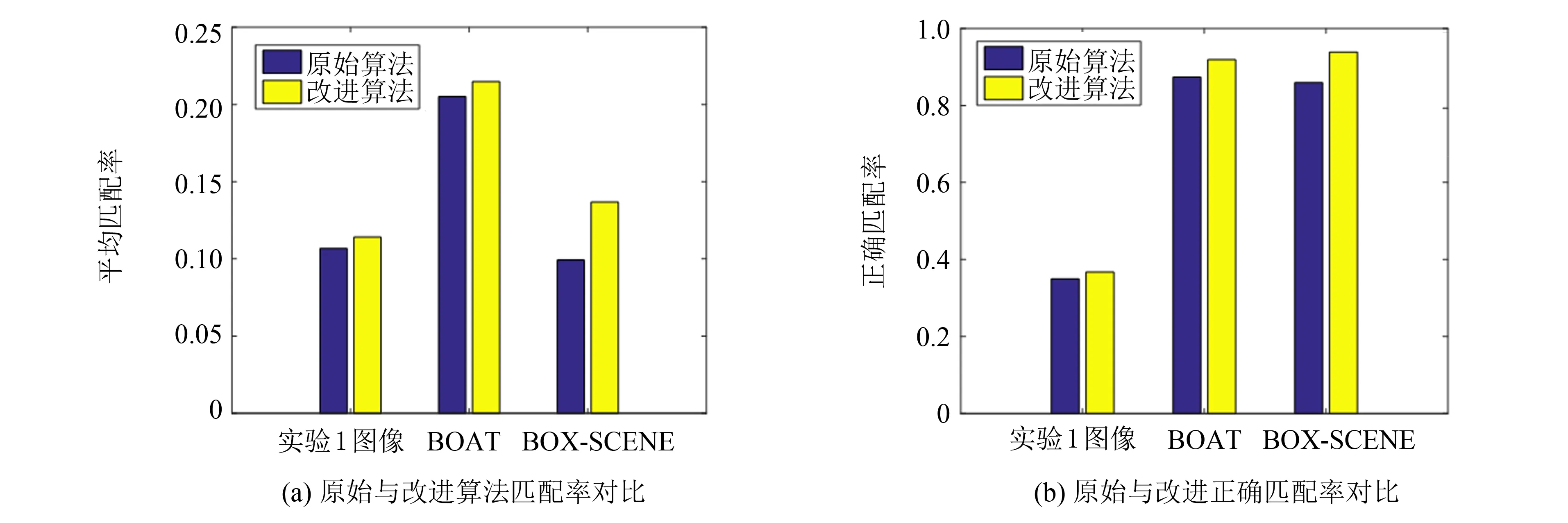
图9 特征点筛选步骤提高了匹配率和正确匹配率Fig.9 Imporvement of matching rate and correct matching rate via feature-point filter step

3.2 测试误匹配去除算法

在实验3中，同样采用SIFT完成粗匹配，然后使用本研究所改进的误匹配去除算法，并记录误匹配去除性能，即误匹配去除所需时间及所剩匹配点数，用于与RANSAC的算法性能相比较，结果如表2所示.

表2 实验3中改进的误匹配去除算法的性能

与RANSAC不同的是，本算法充分利用特征点已知的信息进行排序，然后通过高斯随机采样获取8对匹配样本点用以计算单应矩阵，因此所得到的正确模型时间不会随着样本数量的增加而显著增加. 即相较RANSAC而言，样本数量越多，时间提升效果越好. 从表2可看出，由于匹配集合大，BOAT图像的时间提升效果最为明显. 而即便是匹配点数最少的BARK图像，误匹配去除时间也有了大幅提高. 与RANSAC类似的是，由于采用了随机采样策略，每次误匹配去除所需的时间与正确匹配点的数量均会发生一定的变化. 为测试算法的稳定性，基于BOAT图像，分别运行100次误匹配去除算法，并将其所需时间和正确匹配点数的盒图画出来，如图10所示. 根据上四分位数、下四分位数及中位数可知，剩余正确匹配数量能够稳定地在一个较小的范围内浮动； 而在误匹配去除时间上，由于同时取得8个正确匹配样本的概率小于同时取得4个正确样本的概率，一旦出现错误匹配点，算法会再次重新选取以及计算，因此会有一个相对较大的浮动. 然而最糟糕的情况下，所需的时间也比RANSAC所需的时间少几个数量级，由此可得，本算法可以有效提升误匹配去除性能.

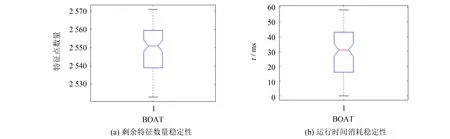
图10 改进误匹配去除算法稳定性测试Fig.10 Stability of improved mismatching elimation algorithm

3.3 测试本改进匹配算法

在分别测试两种改进步骤性能的基础上，设计实验4来测试所提出的改进图像匹配方案的综合性能，并与基于宋佳乾等[12]提出的改进算法结合RANSAC算法的方案、李丹等[14]所提出的改进算法结合RANSAC的方案，及原始图像匹配的方案做出比较. 所用的测试图集为WALL，此图集共包含6张从不同角度拍摄的照片，如图11所示.

图11 WALL图集Fig.11 Image set WALL

此实验中，分别将WALL1与其他图像进行匹配，其中WALL2与WALL1之间拍摄角度变化最小，WALL3次之，而WALL6与WALL1之间拍摄角度变化最大. 图12分别显示各个算法所需运行时间、匹配数量、匹配率及正确匹配率随拍摄角度变化而变化的情况. 图12(a)中，随着角度变化的减少，大部分算法所需的时间都有所增加，这是因为角度变化减少后，图像重叠的部分增多，因此匹配的特征点对增加. 然而，李所改进算法所需的时间却随着角度的增大先减少后增加，这是因为在角度过大的条件下，图像特征点对中只存在很少的匹配对，如图12(b)所示. 但是李改进算法由于仅采用24维的描述子, 易产生过多的误匹配，导致匹配率低(如图12(c)), 因此相应的RANSAC去除误匹配步骤所需时间较多，导致其总耗时呈现随着角度的增大先减少后增加的趋势.宋改进的算法虽然耗时最少, 正确匹配率也最高(如图12(d))，但由于其通过Canny算子去除边沿点, 并通过K-L变换减少描述字维度, 最终只得到很少的匹配数量(如图12(b)). 在算法耗时上，由于本算法增加了去除不稳定特征点的步骤，故较宋改进算法需要额外耗费一定的时间(在Wall图集中，该步骤耗时约400 ms )，但相比于原SIFT算法在速度上仍获得了巨大提升. 由图12(b)和图12(c)可知，因为在特征点计算阶段去除了部分不稳定点，本方案能最大程度上保存SIFT算法所获得的正确特征点，即在数量上最接近SIFT算子且匹配率达到最高. 由此可见，与其他两种改进方案相比，本方案在最大程度上保证匹配效果的基础上，可大幅提高匹配效率.

图12 实验4中不同拍摄角度下的运算性能分析Fig.12 Performance analysis of methodologies in experiment four

4 结语

针对SIFT算法与RANSAC算法相结合的图像匹配过程中，所提取的待匹配特征点数量多、匹配耗时长的问题，提出一种改进的图像匹配方案，引入基于邻域灰度值分布差熵大小的不稳定特征点剔除算法，并对错误匹配剔除算法进行改进. 首先基于特征点邻域的差熵大小筛除SIFT所检测到的特征点进行筛选，以筛除不稳定特征点，而保留大部分正确匹配特征点； 接着对匹配对采用改进的误匹配剔除算法，以快速去除误匹配，最终达到快速、高效、高准确率匹配的目的. 通过一系列实验分别测试不稳定特征点剔除算法和错误匹配剔除算法的性能. 实验结果表明，本方案可以剔除接近一半的不稳定特征点，并且可保存大部分正确匹配的特征点. 因此，与SIFT算法及其改进算法相比较，本特征点筛除算法可在最大程度上保存稳定特征点的基础上, 大大减少匹配所需时间； 而所提出的误匹配剔除算法性能上与RANSAC相当，但能大幅降低去除误匹配所需时间. 联合测试实验的结果表明，相比于SIFT与RANSAC结合的图像匹配方案及已有的改进方案，本研究提出的改进方案能够有效地减少不稳定匹配点，保存大部分稳定特征点，大幅提高匹配率，并快速剔除错误匹配.

[1] YE L W, LIU Z, ZHOU X F，etal. Saliency detection via similar image retrieval[J]. IEEE Signal Processing Letters, 2016, 23(6): 838-842.

[2] FRIDMAN L, LEE J, VICTOR T. ‘Owl’ and ‘Lizard’: patterns of head pose and eye pose in driver gaze classification[J]. IET Computer Vision, 2016, 10(4): 308-313.

[3] SHANG J, CHEN C B, TANG H. Object recognition using rotation invariant local inary pattern of significant bit planes[J]. IET Image Processing, 2016,10(9): 662-670.

[4] LOWE D G. Distinctive image features from scale-invariant keypoints[J]. International Journal of Computer Vision, 2004, 60(2): 91-110.

[5] KASHIF M, DESERNO T M, HAAK D. Feature description with SIFT, SURF, BRIEF, BRISK, or FREAK?: a general question answered for bone age assessment[J]. Computers in Biology and Medicine, 2016, 68(23): 67-75.

[6] CALONDER M, LEPETIT V, STRECHA C,etal. Brief: binary robust independent elementary features[J]. Computer Vision-ECCV, 2010, 67(45): 778-792.

[7] MIKOLAJZYK K, SCHMID C. A performance evaluation of local descriptors[J]. IEEE Transactions on Attern Analysis and Machine Intelligence, 2005, 27(10): 1 615-1 630.

[8] JUAN L, GWUN O. A comparison of sift, pca-sift and surf[J]. International Journal of Image Processing, 2009, 3(4): 143-152.

[9] KHAN N, MCCANE B, MILLS S. Better than SIFT?[J]. Machine Vision and Applications, 2015, 26(6): 819-836.

[10] KE Y, SUKTHANKAR R. PCA-SIFT: a more distinctive representation for local image descriptors[C]//IEEE Computer Society Conference on Computer Vision and Pattern Recognition. Washington D C: IEEE Computer Society, 2004: 506-513.

[11] YU G, MOREL J M. ASIFT: an algorithm for fully affine invariant comparison[J]. Image Processing on Line, 2011, 10(3): 11-38.

[12] 宋佳乾, 汪西原. 基于改进SIFT特征点匹配的图像拼接算法[J]. 计算机测量与控制, 2015, 23(2): 512-515.

[13] DELLINGER F, DELON J, GOUSSEAU Y,etal. SAR-SIFT: a SIFT-like algorithm for SARimages[J]. IEEE Transactions on Geoscience & Remote Sensing, 2015, 53(1): 453-466.

[14] 李丹, 孙海涛, 王海莉. 一种改进的SIFT图像立体匹配算法[J]. 西南交通大学学报, 2015, 50(3): 490-496.

[15] VOURVOULAKIS J, KALOMIROS J, LYGOURAS J. Fully pipelined FPGA-based rchitecture for real-time SIFT extraction[J]. Microprocessors and Microsystems, 2016, 40(4): 53-73.

[16] FISCHLER M A, BOLLES R C. Random sample consensus: a paradigm for model fitting ithapplications to image analysis and automated cartography[J]. Communications of the ACM, 1981, 24(6): 381-395.

[17] NIEDFELDT P C, BEARD R. Recursive RANSAC: multiple signal estimation with utliers[J]. IFAC Proceedings Volumes, 2013, 46(23): 430-435.

[18] HAST A, NYSJO J. Optimal RANSAC: towards a repeatable algorithm for finding the ptimalset[C]//International Conference in Central Europe on Computer Graphics and Isualization (WSCG). Plzen: Journal of WSCG, 2013, 21(1): 21-30.

[19] CHUM O, MATAS J. Matching with PROSAC-progressive sample consensus[C]//IEEE Computer Society Conference on Computer Vision & Pattern Recognition(ICCV). Beijing : IEEE, 2005: 220 -226.