小型双足机器人直行步态的并行规划策略研究

, , ,

(1.上海理工大学 机械工程学院,上海 200093; 2.美钻能源科技(上海)有限公司,上海 200941)

相对于轮式机器人和履带式机器人而言,双足机器人以其类人的行走姿态在多变的地形环境下显示出更好的机动性能[1].玩具机器人、陪伴机器人是双足机器人的重要类别之一,具有外形结构偏于稳定、重心低、行走速度慢等特点.此类机器人因成本考虑多采用成本低廉的舵机或电机实现驱动.目前,双足机器人的研究样机大多躯干结构较大,其行走步态的设计包括建模、步态规划、运动学分析、动力学分析、控制系统设计等步骤[2-4].但这种步态设计方法不适用于此类小型双足机器人.

本文参照人体自然步态中双腿的结构和运动形式,将人体步态轨迹解析为舵机驱动双足机器人的关节转角-时间函数,并对解析的步态数据进行运动学分析.将PWM信号拟合仿真数据,通过对髋关节踝关节的侧向角度调整,得到稳定的步态数据,并将稳定步态下的物理样机步态和虚拟样机数据并行比较,采用并行规划策略完成小型双足机器人直行步态的规划.

1 双足机器人结构

本文参照人体所设计的双足机器人,每条腿具有5个自由度,采用舵机驱动,舵机的输出轴线相互平行或相互垂直,且双足之间舵机分布对称,如图1所示.

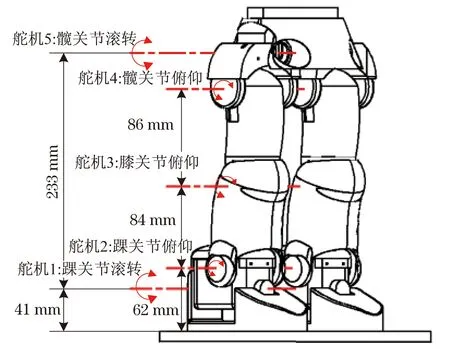
图1 双足机器人自由度分布Fig.1 Biped robot freedom distribution

图1中,舵机1和舵机5用来实现踝关节和髋关节在滚转方向的转动,这两个方向的转动相互配合,完成行走过程中转换重心的工作;舵机2用来实现踝关节俯仰方向的转动,控制单足与地面接触时的角度,用来缓解接触冲击;舵机3用来实现膝关节俯仰方向的转动,在机器人起步状态时对小腿进行收起和机器人在单足落地状态时对小腿进行展开,实现步态的跨越;舵机4用来实现髋关节俯仰方向的转动,在机器人行走状态中对大腿进行收抬.本文所设计的双足机器人用于直行步态稳定行走,因此髋关节未设置偏航自由度.

2 双足机器人位姿分析

步态是在步行运动过程中,步行体的身体各部位在时间和空间上的一种协调关系,步态规划是双足步行机器人研究中的一个关键技术[5].要实现双足机器人的步行,首先需要对双足机器人的位置姿态进行分析.在双足机器人的位姿规划中,D-H方法已经成为了表示机器人和对机器人运动学进行建模的标准方法[6].

本文设计的双足机器人腿部采用D-H方法建立的模型如图2所示.图中,L0,L1,L2,L3分别为躯干中心到髋关节的距离、髋关节到膝关节的距离,膝关节到踝关节的距离,踝关节到足底的距离.O为双足机器人行走方向坐标系,前进方向为x轴,躯体竖直方向为y轴,右手法则确定z轴.O0为躯干中心坐标系,O1,O2,O3,O4分别表示右腿髋关节、膝关节、踝关节、足底坐标系;O5,O6,O7,O8分别表示左腿髋关节、膝关节、踝关节、足底坐标系.

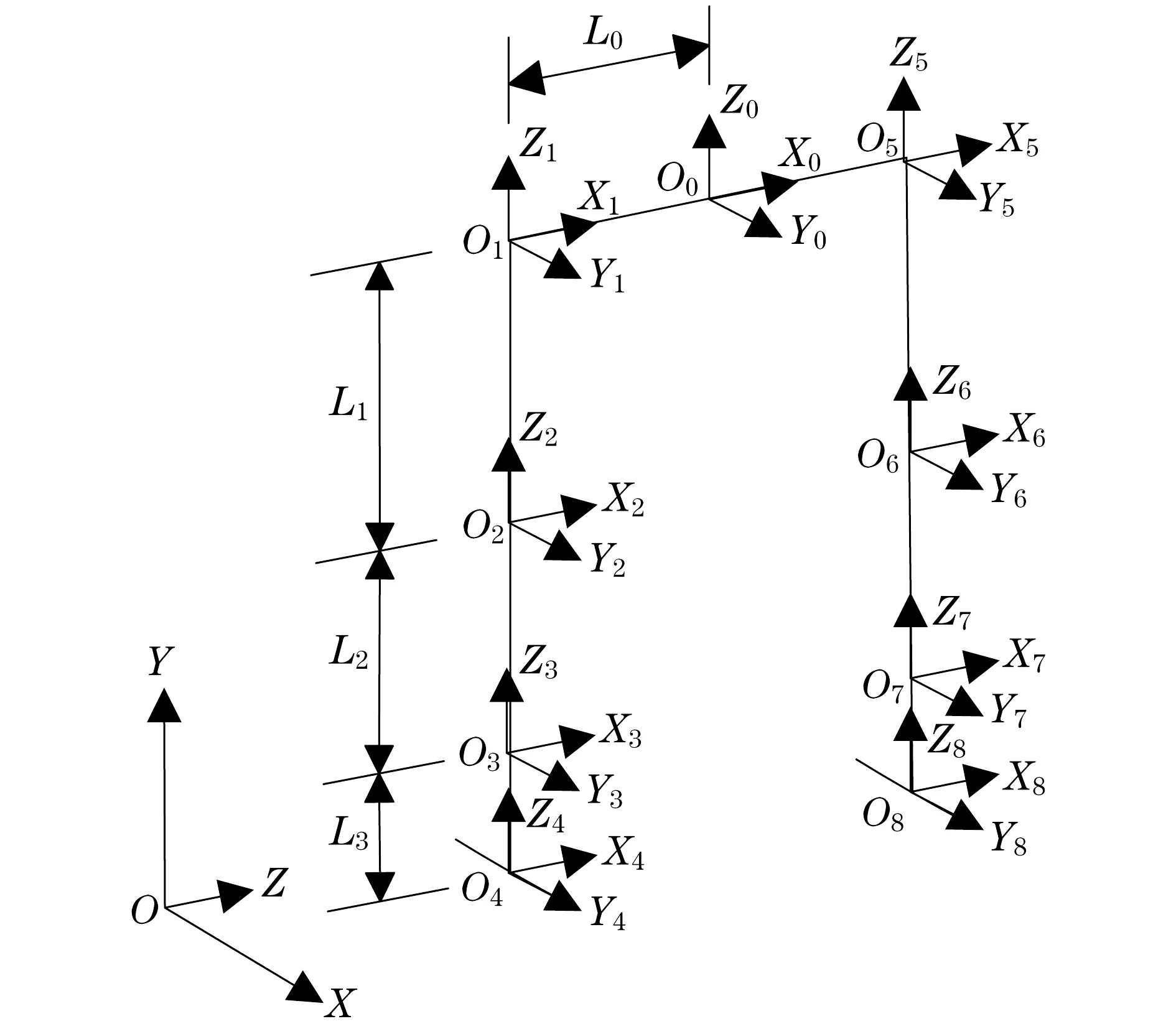
图2 双足机器人D-H坐标系Fig.2 Biped robot D-H coordinate

设定绕坐标轴顺时针旋转方向为正向,图2中O0沿X0负方向平移L0个单位到髋关节处,髋关节在X1方向的旋转角度为θ1,在Y1方向的旋转角度为θ2,则坐标系O0到O1的齐次变换矩阵为

(1)

同理可得坐标系O0到O4的齐次变换矩阵为

因为双足机器人关节舵机是对称布置的,故采用同样方法也可以得到坐标系O0到O7的齐次变换矩阵0T7.

3 双足机器人步态规划

根据双足机器人的行走过程,其步态规划可以相应地分成3个部分[7]:起步步态规划、循环步态规划、止步步态规划.采用5次多项式插值[8-9]的方法来规划运动轨迹,可以使机器关节位置、角速度曲线、角加速度曲线光滑,使得双足机器人行走动作具有平顺性.

3.1 起步步态规划

规划机器人起步阶段所用时间为1 s,步长为60 mm,最大抬腿高度为25 mm,髋关节高度从170 mm下降到148 mm.得到的起步阶段迈步腿踝关节O7在x方向约束条件为

(6)

O7x(T)=4 800t3-14 400t4+11 520t5

(7)

O7在y方向约束条件为

(8)

由式(8)求解5次多项式可得到O7在y方向上位置-时间轨迹关系为

O7y(T)=1 600t2-6 400t3+6 400t4

(9)

同样的方法也可以用来规划迈步腿髋关节O5的轨迹,起步阶段O5在x向和y向的轨迹为

(10)

由式(7)～(10)得到迈步腿踝关节髋关节在x方向和y方向的位置-时间函数关系,对t瞬时髋关节O5、踝关节O7的坐标求运动学逆解,得到迈步腿膝关节O6的坐标.利用MATLAB软件对O5,O6,O7的位置-时间函数进行离散化处理,每隔0.015 s采样一个关节位置点,得到的起步阶段步态棍状图如图3所示.

图3 起步阶段步态棍状图Fig.3 Start gait stick figure

从图3可以看出,支撑腿踝关节O3为坐标原点,踝关节O3到地面高度为62 mm,起步步态规划机器人右足为支撑腿,左足向前迈开一步,步长为60 mm.

3.2 循环步态规划

规划机器人在循环步态中单步所用时间为2 s,步长为120 mm,最大抬腿高度35 mm,髋关节高度保持在148 mm.

循环步态阶段迈步腿踝关节O3在x向和y向的位置-时间轨迹为

(11)

循环步态阶段迈步腿髋关节O1在x向和y向的位置-时间轨迹为

(12)

对式(11)和式(12)求运动学逆解,解得O1,O2,O3的位置-时间函数.利用MATLAB软件对O1,O2,O3的位置-时间函数进行离散化处理,每隔0.015 s采样一个关节位置点,得到的循环步态阶段棍状图如图4所示.

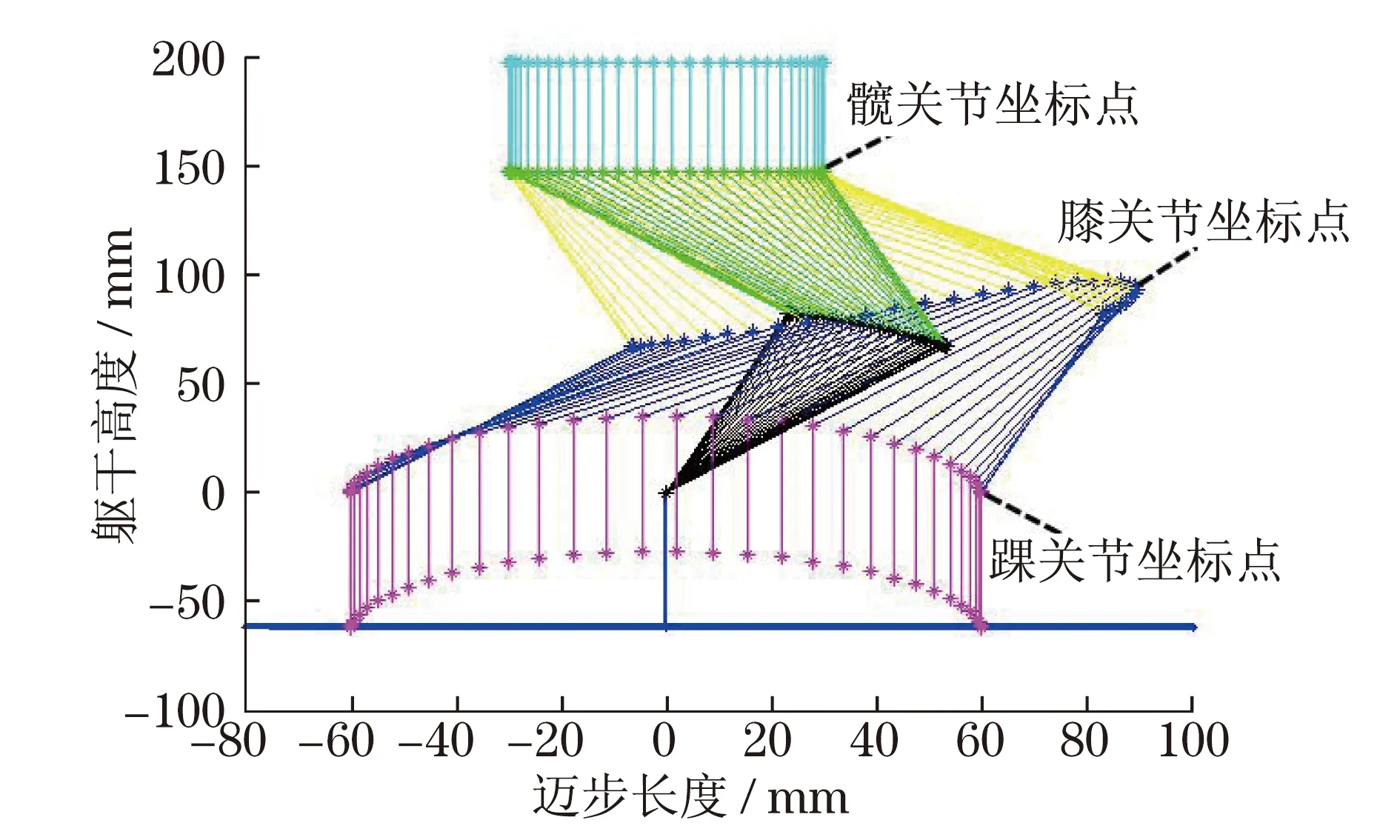
图4 半周期循环步态棍状图Fig.4 Half cycle cyclic gait stick figure

由图4可见,在循环步态中,支撑腿和迈步腿之间间隔了半个步行周期,可将迈步腿和支撑腿的关节数据互换,形成左右腿交替迈开的周期步态[10].

4 双足机器人直行步态并行实现

4.1 并行规划策略简述

本文提出采用并行规划策略来对双足机器人步态进行规划.该策略首先由Matlab计算出双足机器人关节转角-时间函数,再将数据导入虚拟样机和物理样机中.进而通过调整髋关节和踝关节在滚转方向的转动角度来控制机器人侧向的重心偏移,髋关节O1,O5和踝关节O3,O7在滚转方向上相互配合,用于调节机器人在直行步态中的重心转换[11-12](传统双足机器人因质量大、重心高、行走速度快而产生的步行惯性力在小型机器人上的作用较小,故本文在研究中忽略步行惯性力).接下来将规划的步态数据分别导入ADAMS虚拟样机和实际物理样机中.如果物理样机测试中出现行走不稳,则调节步态规划的侧向重心偏移角度.再将调节后的步态数据输入虚拟样机和物理样机中,这样就可以并行比较虚拟样机和物理样机的步态情况.

4.2 运动仿真

将理论分析求解出的双足机器人步态数据导入ADAMS虚拟样机中验证运动学规划的合理性,步行状态如图5所示.

由图5可以看出,机器人可以按规划的轨迹直行,肢体的运动显示关节处不存在限位的情况,说明机器人外形结构设计合理.

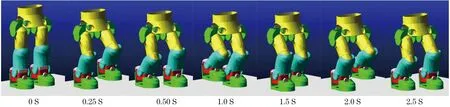
图5 双足机器人在ADAMS中步行状态截图Fig.5 Biped robot walking status screenshots in ADAMS

4.3 物理样机测试

物理样机在直行步态中发生重心不稳时,对髋关节和踝关节滚转方向的角度进行调整,使得机器人处于单脚支撑状态时,机器人的躯干重心落在支撑腿的支撑面积内.将循环步态中单周期的步态进行循环延伸,得到双足机器人每个关节的转角-时间函数.测试得到的稳定步行状态下各关节的转角-时间函数如图6和图7 (见下页)所示.

由图6～7可以看出,双足机器人关节最大转角发生在膝关节处,最大转角为96.69°.在0～0.5 s,机器人处于起步状态,左腿先向前迈一步,左踝关节、左髋关节、左膝关节在0.25 s左右达到转角峰值,在0.5 s时完成左足的着地,0～0.5 s完成双足机器人的起步状态.

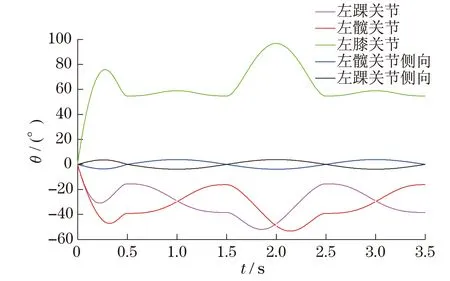
图6 左腿关节转动-时间函数Fig.6 Left leg joint angle-time function

图7 右腿关节转动-时间函数Fig.7 Right leg joint angle-time function

0.5～1.5 s时间段,右腿向前迈一步,左腿处于支撑状态,右腿膝关节在1 s时达到转角峰值,在1.5 s时完成右足的着地.1.5～2.5 s时间段,左腿向前迈一步,右腿处于支撑状态,左腿膝关节在2 s时达到转角峰值,在2.5 s时完成右足的着地.0.5～2.5 s完成双足机器人的循环步态.

将舵机的PWM信号对双足机器人关节转角-时间函数进行拟合,得到每个关节舵机的转角-时间函数,运动仿真的情况和实际物理样机实时对比,规划出双足机器人物理样机直行步态截图如图8所示.

在物理样机下测试得到稳定的步态后,可以在ADAMS后处理模块,考察当前稳定步态下双足机器人在虚拟样机中的两足运动变化曲线.双足机器人的左、右足中心和躯干中心在y方向的移动轨迹如图9所示.

图8 双足机器人物理样机直行步态截图Fig.8 Biped robot physical prototype straight gait screenshots

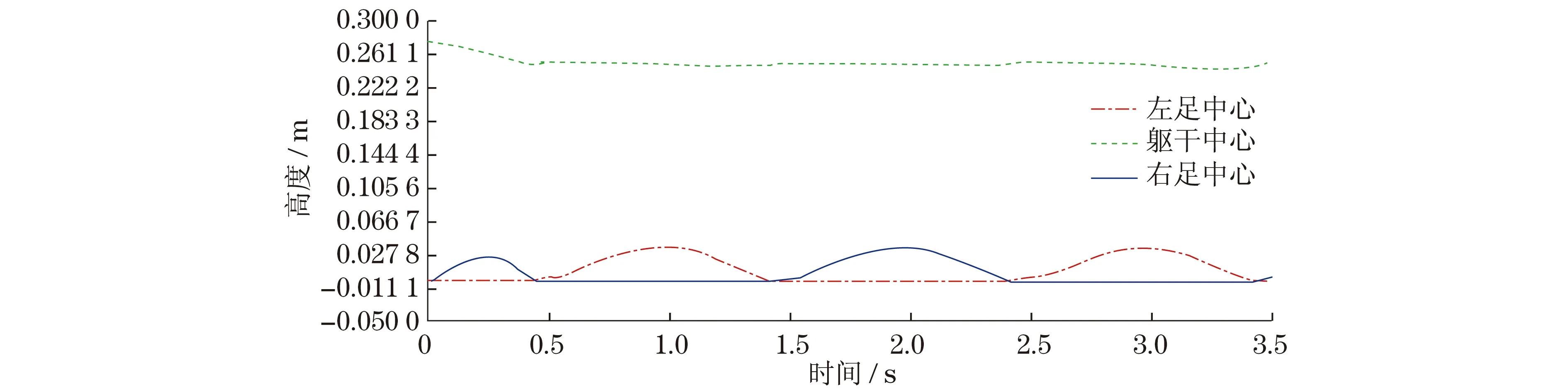
图9 左、右足和躯干中心在y方向位移Fig.9 Right foot,left foot and trunk center’s displacements in y direction

由图9可以知道,机器人躯干中心随着双足的前进而前进,机器人躯干中心在起步时由277.2 mm下降至250.6 mm,在循环步态时候一直保持在250 mm左右.双足机器人躯干中心在z方向的速度变化如图10所示.

图10 躯干中心在z方向速度Fig.10 Trunk center speed in z direction

由图10可以看出,5次多项式插值的轨迹规划在速度变化上是光滑的,0.5 s处出现速度波动是由于该时刻为起步步态和循环步态的交接处[13].

5 结 论

本文通过仿人姿态分析,设计仿人结构的双足机器人,采用5次多项式插值的方法规划出髋关节和踝关节的运动轨迹,利用代数解析法求解出各个关节的转角-时间函数.通过并行规划策略实现物理样机直行步态的规划,将数据分别导入ADAMS虚拟样机和实际物理样机进行并行比较测试.机器人的步态规划通过物理样机反馈给虚拟样机进行调整对比,提高了小型双足机器人步态规划的效率.

[1] 敬成林,朱晓铭.双足机器人行走控制算法的三维仿真研究[J].计算机仿真,2014,31(3):346-349.

[2] 司媛媛,何斌.基于CPG和小脑模型的双足机器人行走控制[J].系统仿真技术,2017,13(1):6-10.

[3] 查望华.双足机器人运动控制系统的研究[D].杭州:浙江大学,2016.

[4] ZHU H B,LUO M Z,ZHAO J H,et al.Soft landing control strategy for biped robot[J].Industrial Robot:An International Journal,2017,44(3):312-323.

[5] 李春光,刘国栋.双足机器人自然ZMP轨迹生成方法研究[J].计算机工程与应用,2014,50(19):53-57.

[6] NIKU S B.Introduction to robotics:analysis,control,applications[M].2nd ed.New York:Wiley & Sons,2011.

[7] 赵川,张鹏超,潘晓磊,等.机器人的运动轨迹插值方法研究与分析[J].制造技术与机床,2016(6):65-69.

[8] 史耀强.双足机器人步行仿真与实验研究[D].上海:上海交通大学,2012.

[9] 杨萍,樊迪.小型双足机器人步态规划研究[J].机械制造,2015,53(9):39-41.

[10] ZANG X Z,LIU Y X,LIU X Y,et al.Design and control of a pneumatic musculoskeletal biped robot[J].Technology and Health Care,2016,24(S2):S443-S454.

[11] YAMAMOTO K.Control strategy switching for humanoid robots based on maximal output admissible set[J].Robotics and Autonomous Systems,2016,81:17-32.

[12] 郭发勇.仿人双足机器人多地形步态规划和稳定控制方法研究[D].合肥:中国科学技术大学,2016.

[13] SHAH N H,YEOLEKAR M A.Influence of slope angle on the walking of passive dynamic biped robot[J].Applied Mathematics,2015,6(3):54411.