带有接种的随机SIS传染病模型研究

,,

(1.上海健康医学院 文理教学部,上海 201318; 2.上海健康医学院 护理与健康管理学院,上海 201318)

1 问题的提出

人们一直都很重视传染病的预防与控制.数学模型在研究传染病动力学方面具有相当重要的意义.通过建立数学模型来描述和分析传染病传播的数据规律并结合计算机进行数值模拟,可以揭示传染病的传播机理、生物因素、社会影响以及疾病流行规律,寻找疾病流行的关键因素,预测疾病发生发展的趋势,进而建立遏制疾病蔓延的手段和最优控制策略.

在现实世界里,由于疾病的发生、发展和传播是一个非常复杂的过程,其中会存在许多现实不确定因素(如疾病的传播机理和传播途径),同时,还不可避免地会受到各种不可预知的环境噪声干扰(如洪水、大旱、海啸等),这些噪声和不确定因素的存在都会对疾病的传播造成很大的影响.然而,对那些具有不确定因素和易受噪声干扰的疾病传播过程进行有效的控制和预测又是一件非常困难的事情.因此,如何刻画这些随机不确定因素对疾病传播的影响就显得非常重要且具有实际意义.近年来,已有很多作者研究随机传染病模型[1-10].

由于相关扰动的复杂性带来一定的研究难度,因此,研究确定性传染病模型在环境噪声扰动下的动力学性质更具有实际意义.随机传染病模型的研究无论是理论还是研究方法都与确定性模型有比较大的差别,这方面还有大量的研究工作有待进一步开展.

Li等[11]研究了带有时滞的接种SIS模型,其形式为

(1)

式中:S(t)为易感者的数量;I(t)为染病者的数量;V(t)为接种者的数量;A为新生者常数输入率,A>0;μ为自然死亡率;q为输入者被接种的比例,0≤q≤1;α为因病死亡率,α≥0;p为易感者被接种率,p≥0;β为传染率系数,β≥0;γ为染病者的回复率,γ≥0;τ为免疫期.

对于模型(1),基本再生数

当R0<1时,模型(1)总存在无病平衡点

是全局渐近稳定的.

当R0>1时,无病平衡点E0是不稳定的,此时存在唯一的地方病平衡点E*=(S*,I*,V*)是局部渐近稳定的.

在实际生活中,环境白噪声不可避免地会对模型(1)造成影响,故在模型(1)的基础上建立相应的随机模型,研究在干扰情况下疾病何时消失、何时流行.相对于模型(1),考虑具有如下形式的随机模型:

(2)

式中:Bi(t)是定义在完备概率空间上的相互独立标准布朗运动,i=1,2,3;σi表示环境白噪声的强度,i=1,2,3.

由于V(t) 在疾病的传输中没有影响,现只考虑模型

(3)

在本文中,总假设(Ω,F,{Ft}t≥0,P)为完备的概率空间,其中,{Ft}t≥0是Ω上的一个σ-代数且满足通常条件(即右连续,F0包含所有零测集).

2 主要结果

对于定理1的证明可以构造函数

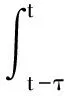
式中,a为正常数.

利用文献[6-7]的方法可证明定理1的结论成立.

为方便起见,记

(4)

定义

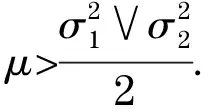
(5)

其中

为了证明定理2,先引入几个有用的引理.

引理1[7]令(S(t),I(t))是模型 (3) 满足任意初值(S(0)>0,I(ζ)≥0)(ζ∈[-τ,0),I(0)>0)的解,则有如下结论:

(6)

(7)

利用上述两个模型分别算出的转移概率矩阵，定义风险概率临界值，矩阵中高于临界值的概率，本模型认为属于正常交易顺序；反之则属于异常交易顺序。模型首先人工设置风险概率临界值的初始值，随后输入包含正常交易序列和异常交易序列的训练集，根据分类效果动态调整风险概率临界值的大小，通过多次训练，得到识别效果最好的临界值。

引理3[7]设f(t)∈C[[0,)×Ω,(0,)]和F(t)∈C[[0,)×Ω,R].若存在正常数λ0,λ,使得

现证明定理2.

证明

对上式两端从0～t积分,积分后两端同时除以t,可得

整理可得

(8)

其中

显然,由引理1和引理2可得

(9)

定义W(I(t))=logI(t),并利用Ito公式,可得

d logI(t)=[βS(t)-(μ+γ+α)

(10)

对式(9)两端从0～t积分并除以t,可得

(11)

将式(8)的〈S(t)〉 带入式(11)中,并整理得

(12)

3 结束语

同相应的确定性传染病模型相比较,随机系统的阈值与环境白噪声的强度相关.从本文中的结论可以看出:当白噪声的强度较小时,随机系统与对应的确定系统具有相似的性质,即随机系统的阈值小于1,疾病灭绝;当白噪声的强度较大时,随机系统会出现完全不同于确定系统的性质,即使确定系统的阈值大于1,在强噪声的干扰下仍可以导致疾病灭绝.在实际中,这种大的噪声可以理解为突发的恶劣天气、严重的自然灾难等.与确定系统相比,随机系统的研究刚刚起步,今后进一步研究与白噪声相关的理论问题和应用问题具有广阔的应用前景.

[1] JI C Y,JIANG D Q,SHI N Z.The behavior of an SIR epidemic model with stochastic perturbation[J].Stochastic Analysis and Applications,2012,30(5):755-773.

[2] GRAY A,GREENHALGH D,HU L,et al.A stochastic differential equation SIS epidemic model[J].SIAM Journal on Applied Mathematics,2011,71(3):876-902.

[3] JIANG D Q,YU J J,JI C Y,et al.Asymptotic behavior of global positive solution to a stochastic SIR model[J].Mathematical and Computer Modelling,2011,54(1/2):221-232.

[4] ARTALEJO J R,ECONOMOU A,LOPEZ-HERRERO M J.On the number of recovered individuals in the SIS and SIR stochastic epidemic models[J].Mathematical Biosciences,2010,228(1):45-55.

[5] LU Q Y.Stability of SIRS system with random perturbations[J].Physica A:Statistical Mechanics and its Applications,2009,388(18):3677-3686.

[6] ZHAO Y N,JIANG D Q,O′REGAN D.The extinction and persistence of the stochastic SIS epidemic model with vaccination[J].Physica A:Statistical Mechanics and its Applications,2013,392(20):4916-4927.

[7] ZHAO Y N,JIANG D P.The threshold of a stochastic SIS epidemic model with vaccination[J].Applied Mathematics and Computation,2014,243:718-727.

[8] JI C Y,JIANG D Q.Threshold behaviour of a stochastic SIR model[J].Applied Mathematical Modeling,2014,38(21/22):5067-5079.

[9] LIN Y G,JIANG D Q,WANG S.Stationary distribution of a stochastic SIS epidemic model with vaccination[J].Physica A:Statistical Mechanics and its Applications,2014,394:187-197.

[10] LAHROUZ A,SETTATI A.Necessary and sufficient condition for extinction and persistence of SIRS system with random perturbation[J].Applied Mathematics and Computation,2014,233:10-19.

[11] LI J Q,MA Z E.Global analysis of SIS epidemic models with variable total population size[J].Mathematical and Computer Modelling,2004,39(11/12):1231-1242.

[12] MAO X R.Stochastic differential equations and applications[M].2nd ed.Chichester,UK:Horwood Publishing Limited,2008.