球面并联机构功耗比评价指标及性能分析

侯雨雷 魏晓晨 周治宇 曾达幸

燕山大学机械工程学院，秦皇岛，066004

0 引言

机构的性能评价指标是对机构进行性能分析与设计的基础和前提。并联机构的性能评价指标一直是国内外机构学领域的热点和难点。承载能耗与总能耗功率的比例偏低是仿生机构难以应用于实际的关键问题之一，故而，具有明确的物理意义、可用数学方程描述、具有可计算性的功耗性能指标的定义对研究仿生关节并联机构具有重要意义。

三自由度球面并联机构作为适用于肩关节仿生的重要机构之一[1]，其功耗传递效率直接影响机构的承载性能。苑飞虎等[2]以六自由度并联机构为例，分析了位姿对承载能力与承载性能指标的影响。KORAYEM等[3-4]结合并联机构的具体应用，研究了沿固定轨迹运动时机构的承载能力。

并联机构瞬时状态下的功耗传递能力即为机构的瞬时传递功率，而功率又能够反映并联机构运动和力的传递性能。迄今针对功率传递的分析已取得许多成果。文献[5-6]将广义传递力矩螺旋引入机构静力传递特性的评价中，并定义了机构的传递特性和可操作性综合性能评价指标。WANG等[7]基于螺旋理论互易积理论，结合能效系数，定义了并联机构运动/力传递性能评价指标。刘辛军等[8-10]以5R机构为例，提出了一类与坐标系无关的静力传递性能评价指标，解决了在不同形式的运动旋量和力旋量的组合下，传递功率最大值的求解问题，增强了文献[7]所述评价指标计算模型的实用性与时效性。

并联机构的雅可比矩阵能够反映驱动端运动与执行器运动的映射关系，故而，基于雅可比矩阵定义相应的并联机构性能指标，可用于评价机构的传递性能。YOSHIKAWA[11-12]基于雅可比矩阵奇异值分解原理，提出了串联机器人可操作度指标，用以分析机构运动/力的传递性能。季晔等[13]通过对一种四自由度并联机构的雅可比矩阵进行求导分析，绘制出机构承载力与驱动力性能图谱。

本文以3PSS/S(P表示移动副，S表示球副)和3RRR(R表示转动副)球面并联机构为研究对象，在运动学分析的基础上，引入功耗比性能指标，建立两种机构的功耗比数学模型并进行数值对比分析，结合3PSS/S并联样机进行功耗比实验，并与理论功耗比曲线进行对比，以验证功耗比性能指标的有效性。

1 球面并联机构功耗比数学模型

3PSS/S与3RRR[14]并联机构均具有三转动自由度，可作为肩关节仿生机构。本文以此两个机构为研究对象，设定各自机构参数及相同的运动轨迹，并在此基础上进行两类机构的功耗比性能分析。

1.1 3PSS/S并联机构功耗比数学模型

图1所示为3PSS/S球面并联仿生肩关节机构[15]，它主要由定平台、动平台、三条对称的PSS运动支链和一个中间球副S支链组成，H为中间球副的球心(机构的转动中心)。建立固定坐标系Hxyz，z轴沿HO1向上为正，x轴在z轴与HA1所决定的平面且垂直于z轴，方向指向杆A1B1所在一侧。建立与动平台固连的动坐标系O1uvw，其中，w轴垂直于动平台向上为正，u轴沿B1O1方向指向B1。h为HO1的间距，ε是定平台三棱锥O2C1C2C3的结构参数，L1为三条支链定长杆的杆长，L2为与动平台相连的三个球副所在外接圆的半径。

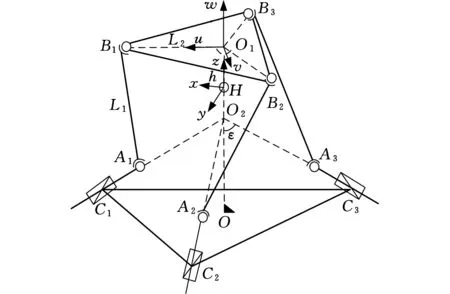
图1 3PSS/S并联肩关节机构简图Fig.1 Schematic diagram of the 3PSS/S parallel shoulder joint mechanism

设定此三转动并联机构动平台输出角速度矢量ω=(ωx,ωy,ωz)T、所受外力Fg=(fx,fy,fz)T、外力矩Mg=(Mx,My,Mz)T，则驱动关节速度矢量

ν=J-1ω=(v1,v2,v3)T

(1)

输入力矢量

Fr=JTMg=(F1,F2,F3)T

(2)

式中，v1、v2、v3为三个驱动关节的移动速度；F1、F2、F3为三个驱动关节的驱动力；J为速度雅可比矩阵。

机构的输出功率Po为动平台分别在x、y、z轴方向的角速度与各自方向上所受力矩乘积的代数和，即

Po=Mxωx+Myωy+Mzωz

(3)

当动平台沿既定轨迹运动时，驱动电机对动平台所做功并非全为正功，考虑到驱动电机的实际耗能，机构的实际输入功率Pi为各驱动电机输出功率绝对值的代数和，即

Pi=|F1v1|+|F2v2|+|F3v3|

(4)

为衡量不同位姿下功耗传递性能，定义功耗比性能指标为

K=Po/Pi

(5)

由定义式可知，K≤1。K值越大，驱动电机所做有效功越多，机构功耗传递性能越佳；反之，驱动电机的输出功耗转换成的机构输出功耗越少，机构功耗传递性能越差。

1.2 3RRR并联机构功耗比数学模型

如图2所示，取3RRR并联机构球心点O为坐标系原点的中心，按照D-H连杆坐标系规定的方法建立坐标系Ox0y0z0、Oxyz和Oxijyijzij(i,j=1,2,3,分别表示第i分支的第j转动副)，令ui、vi、wi(i,j=1,2,3)分别表示坐标轴zi1、zi2、zi3(i=1,2,3)在定坐标系下的单位矢量。

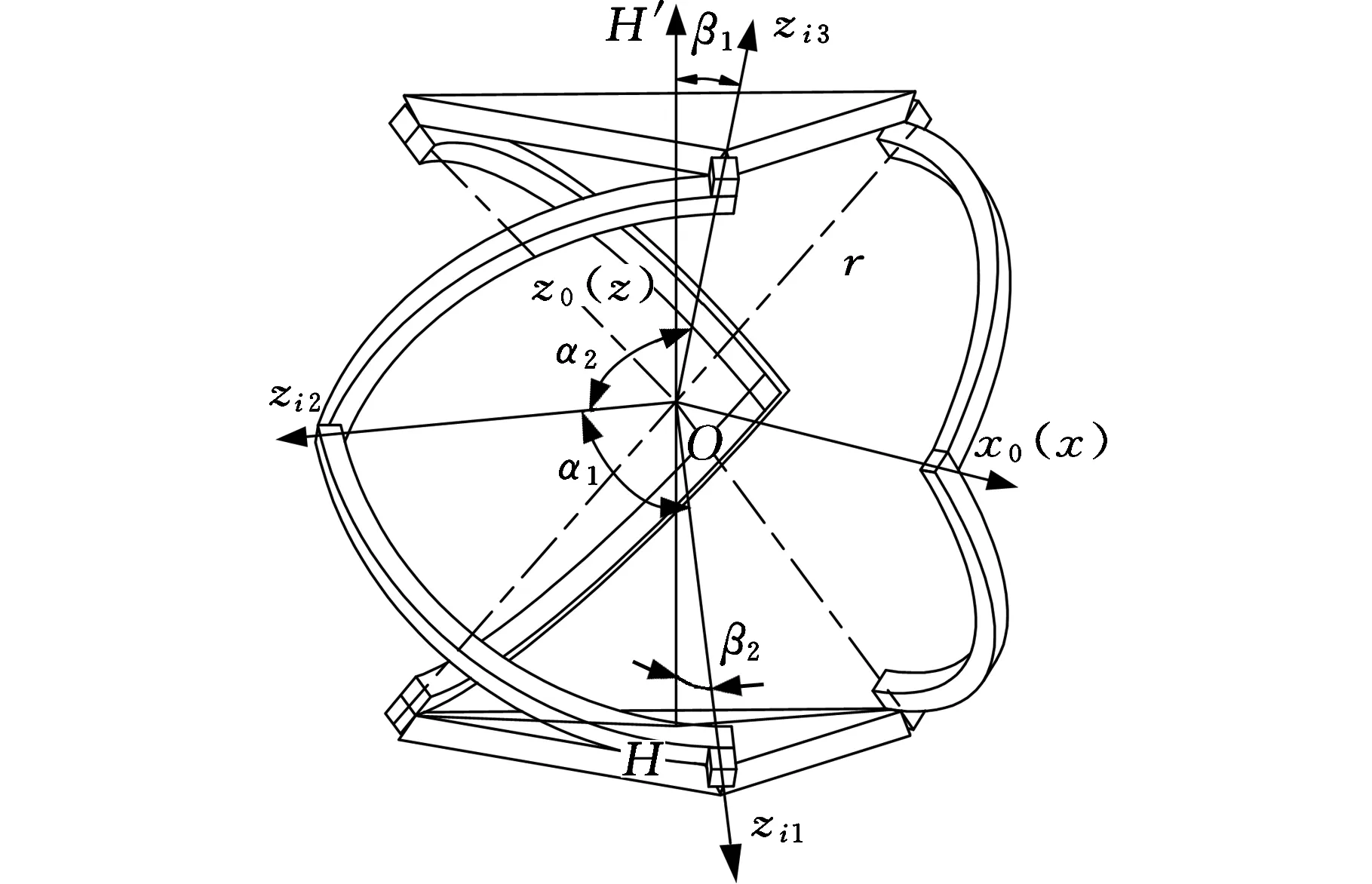
图2 3RRR并联机构简图Fig.2 Schematic diagram of the 3RRR parallel mechanism

机构的结构参数表示如下：α1为zi1轴与zi2轴的夹角，α2为zi2轴与zi3轴的夹角，β1为zi3轴与OH′(H′为动平台的中心点)的夹角，β2为zi1轴与OH(H为定平台的中心点)的夹角，η1i(i=1,2,3)为zi1轴在下平台的投影与z11轴投影所成的角，η2i(i=1,2,3)为zi3轴在上平台的投影与z13轴投影所成的角度。

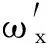
ω′=G-1ωc=(ω1,ω2,ω3)T

(6)

输入力矩为

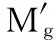
(7)

式中，ω1、ω2、ω3为三个驱动关节角速度;M1、M2、M3为三个驱动关节转动力矩;G为运动雅可比矩阵。

进而，3RRR并联机构功耗比表达式为

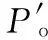
(8)

2 并联机构功耗比数值计算

为方便分析，对于3PSS/S和3RRR并联机构，统一采用RPY角描述其动平台姿态，设定两并联机构的工作空间半径r′=80 mm，其中3RRR并联机构的尺寸参数如下：α1=90°，α2=90°，β1=60°，β2=45°，η11=η21=0°，η12=η22=120°，η13=η23=240°，球面机构半径r1=80 mm。3PSS/S的尺寸参数如表1所示。

表1 3PSS/S并联机构的尺寸参数

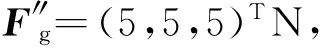
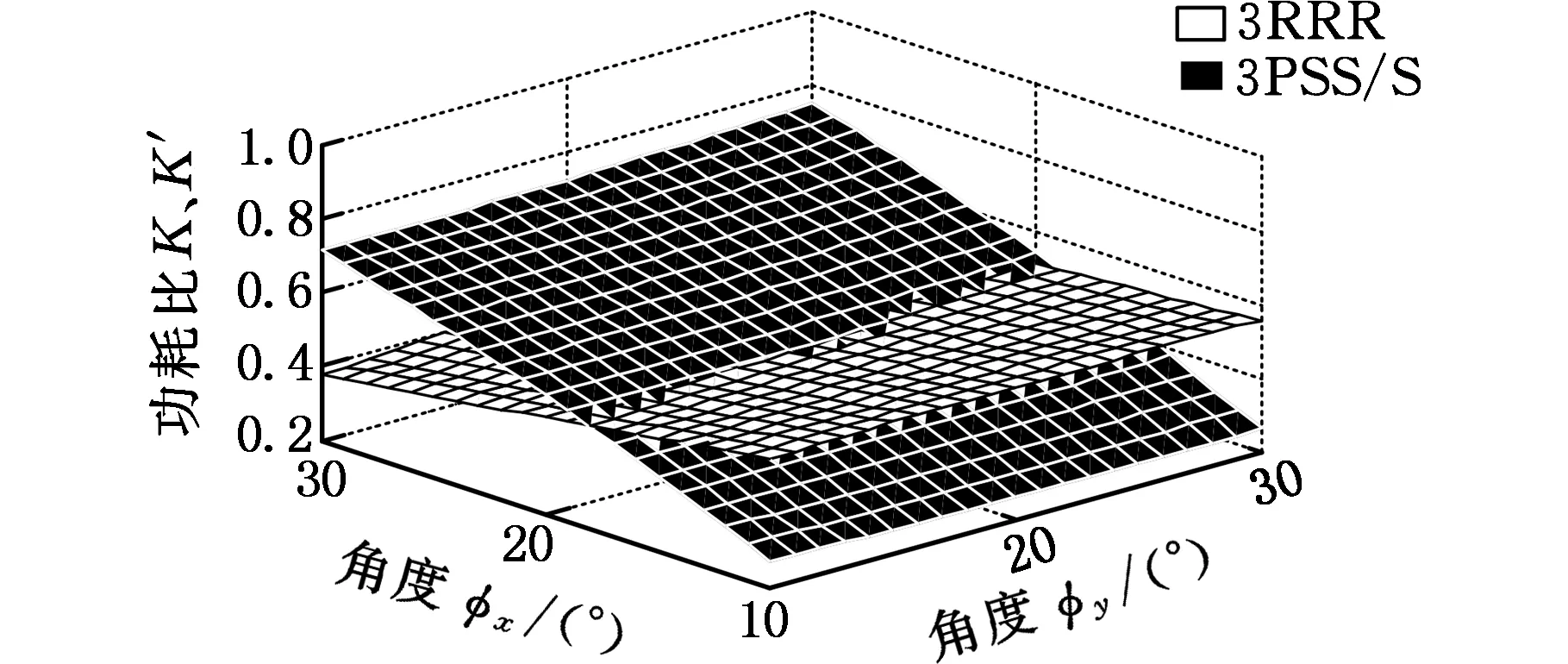
(a)φz=10°

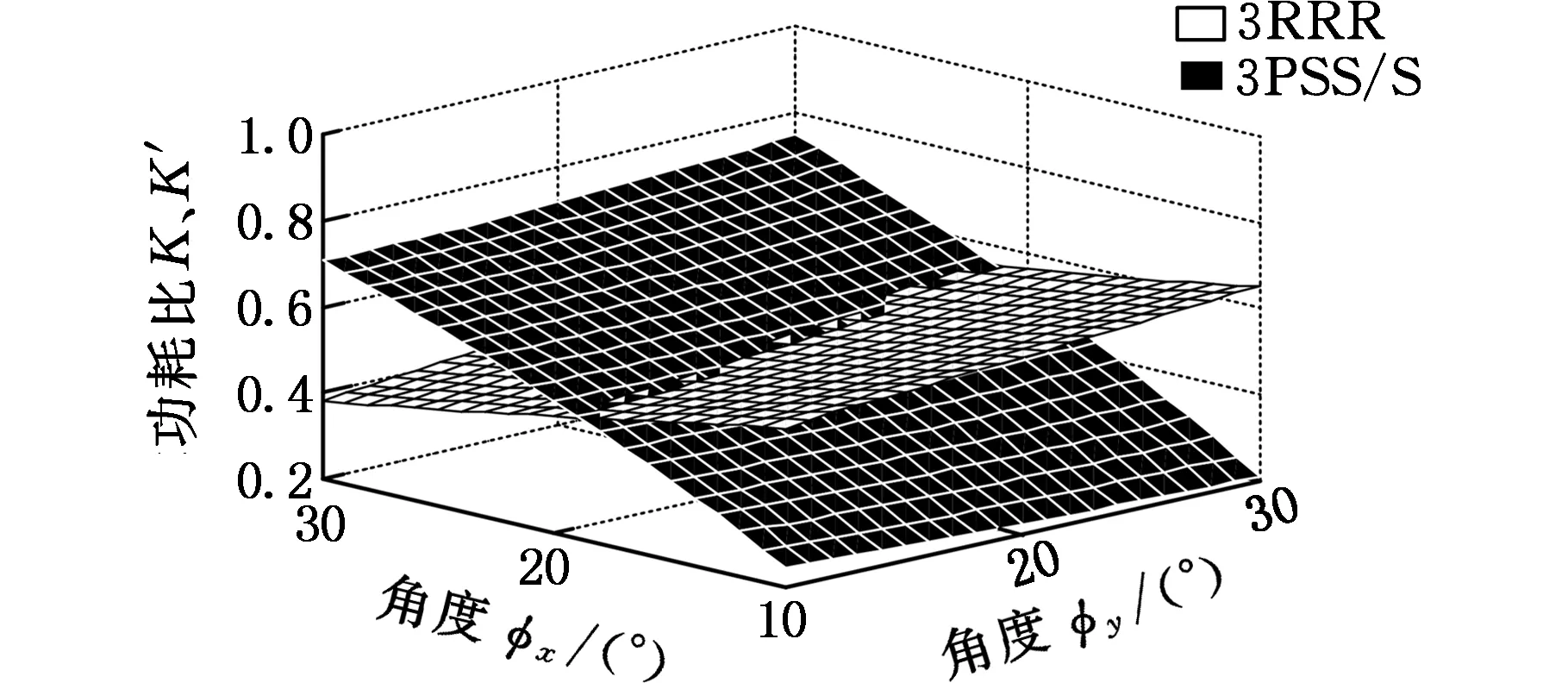
(b)φz=20°

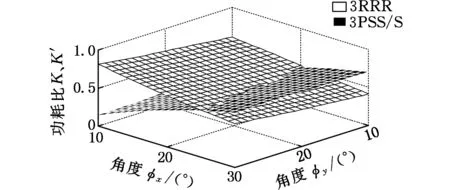
(c)φz=30°图3 动平台正向转动时3PSS/S与3RRR机构功耗比对比Fig.3 Power consumption ratio comparison between 3PSS/S and 3RRR mechanism when the moving platform rotates in the forward direction

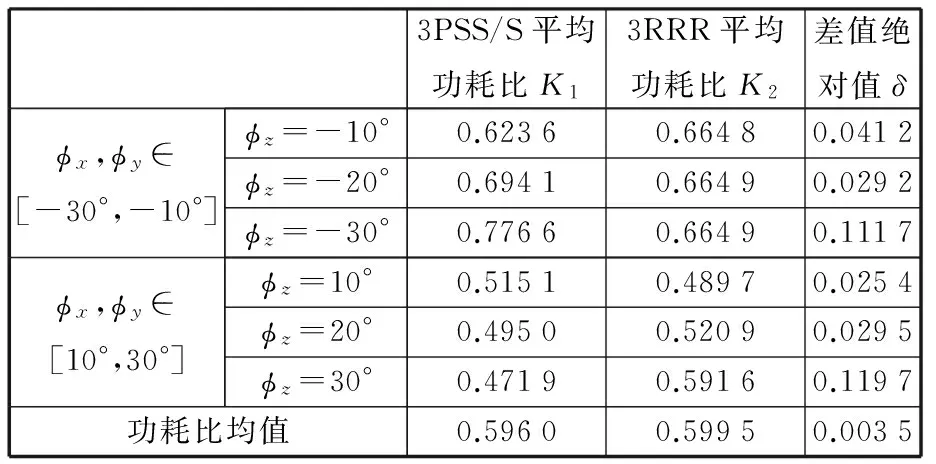
选定3PSS/S与3RRR机构动平台绕固定坐标系x、y、z轴逆向转动，定义姿态角φz分别等于-10°、-20°、-30°，φx、φy同时在步长为1°的区间[-30°,-10°]内变化时，两并联机构功耗比变化趋势对比如图4所示，计算、整理功耗比均值如表2所示。由表2可知，在上述工作空间范围内，3RRR并联机构功耗比平均值较大，为0.599 5，而3PSS/S并联机构功耗比平均值与其相差0.003 5，占比为0.583 8%，由此可见，在此工作空间内，两并联机构功耗传递性能基本相当。

3 3PSS/S并联样机功耗比实验及其分析

如图5所示，3PSS/S并联肩关节样机[16]由机械本体、伺服电机和控制柜等单元组成。在样机动平台中心安装陀螺仪传感器，通过串口转换器将测量得到的动平台角度及角速度数据实时反馈至上位机，进而通过数据处理得到负载对动平台的广义力矩。与此同时，通过运动控制器的数据采集系统，获取驱动伺服电机的扭矩输出量。

不妨设定动平台姿态角φx=0°、φy=0°、φz=-15°为初始启动姿态，在动平台上放置质量为2 kg的圆柱状负载，通过轨迹规划，设定机构移动副驱动的输入数据，如表3所示。在驱动电机的控制下，三个移动副从位置1到位置9依次运动，图6所示为移动副在位置2、位置4、位置6、位置8等不同换向位置时，机构的运动状态。

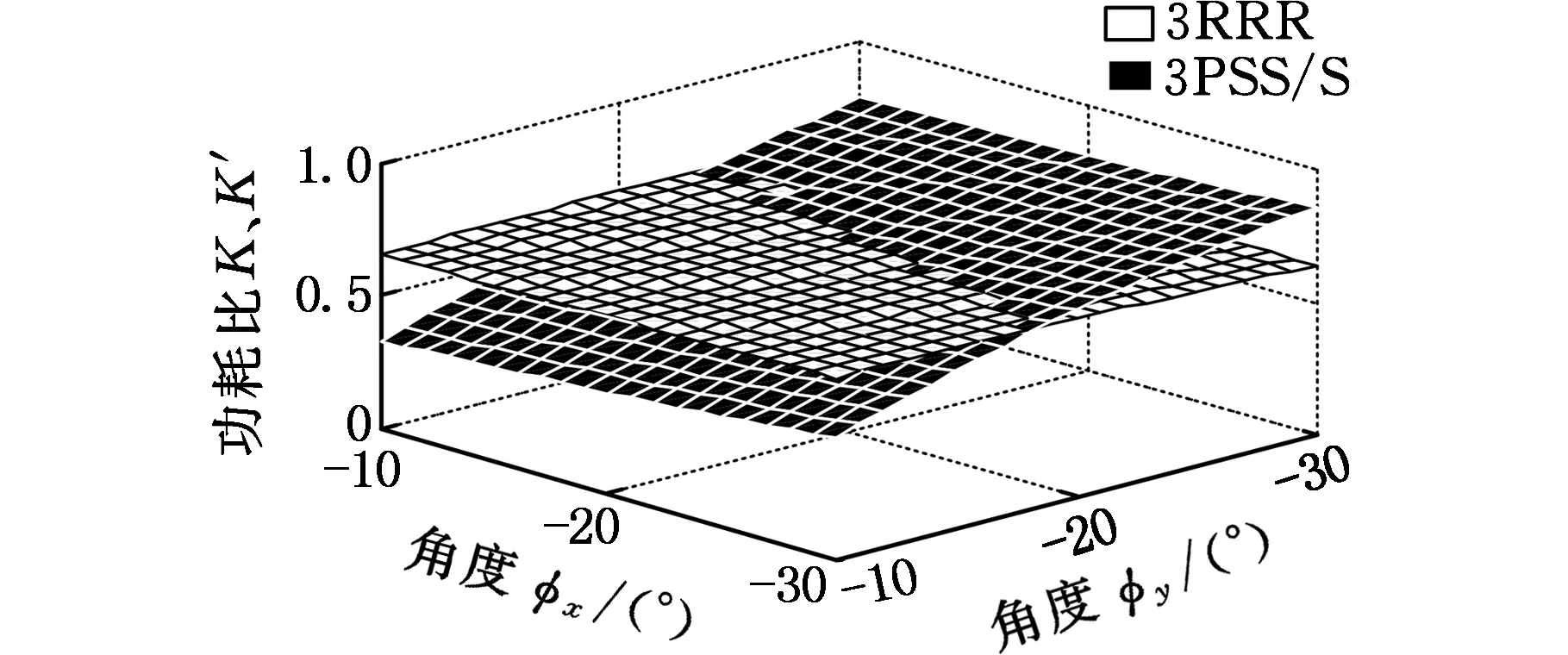
(a)φz=-10°

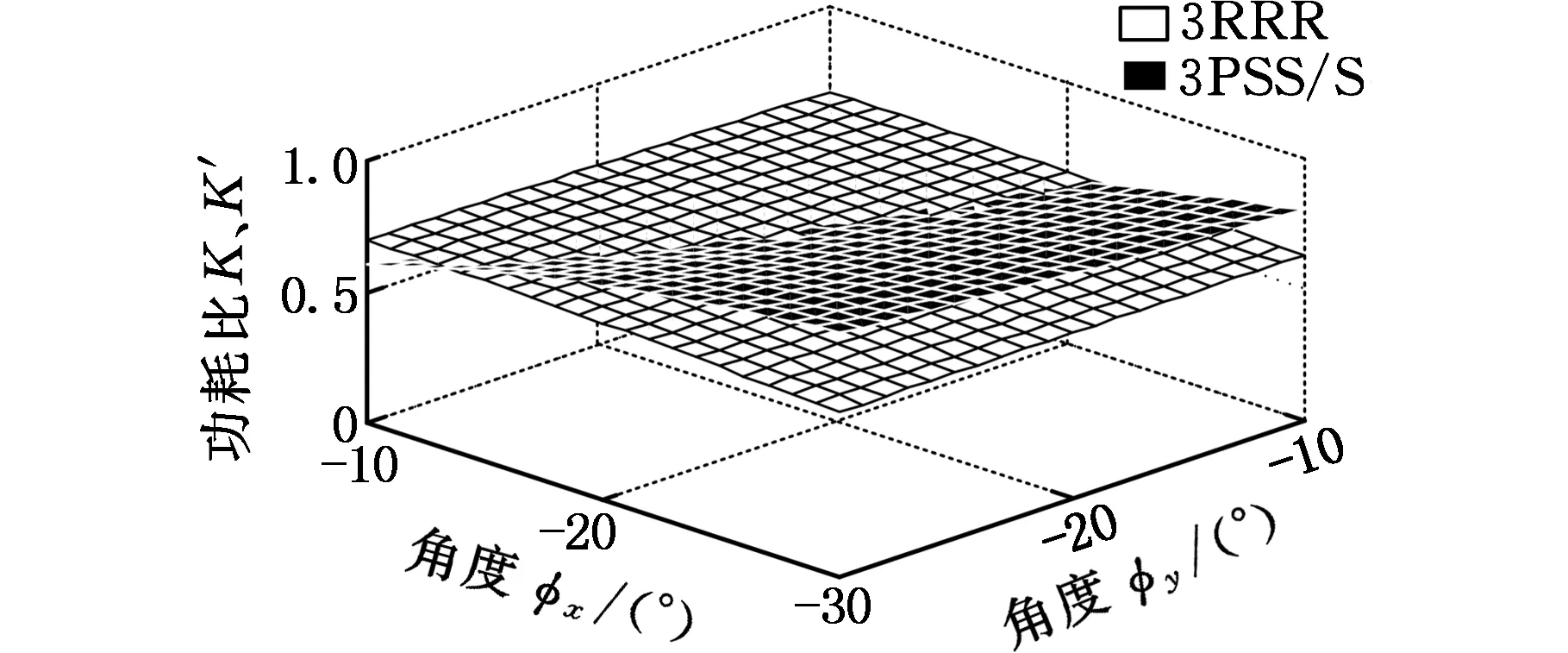
(b)φz=-20°

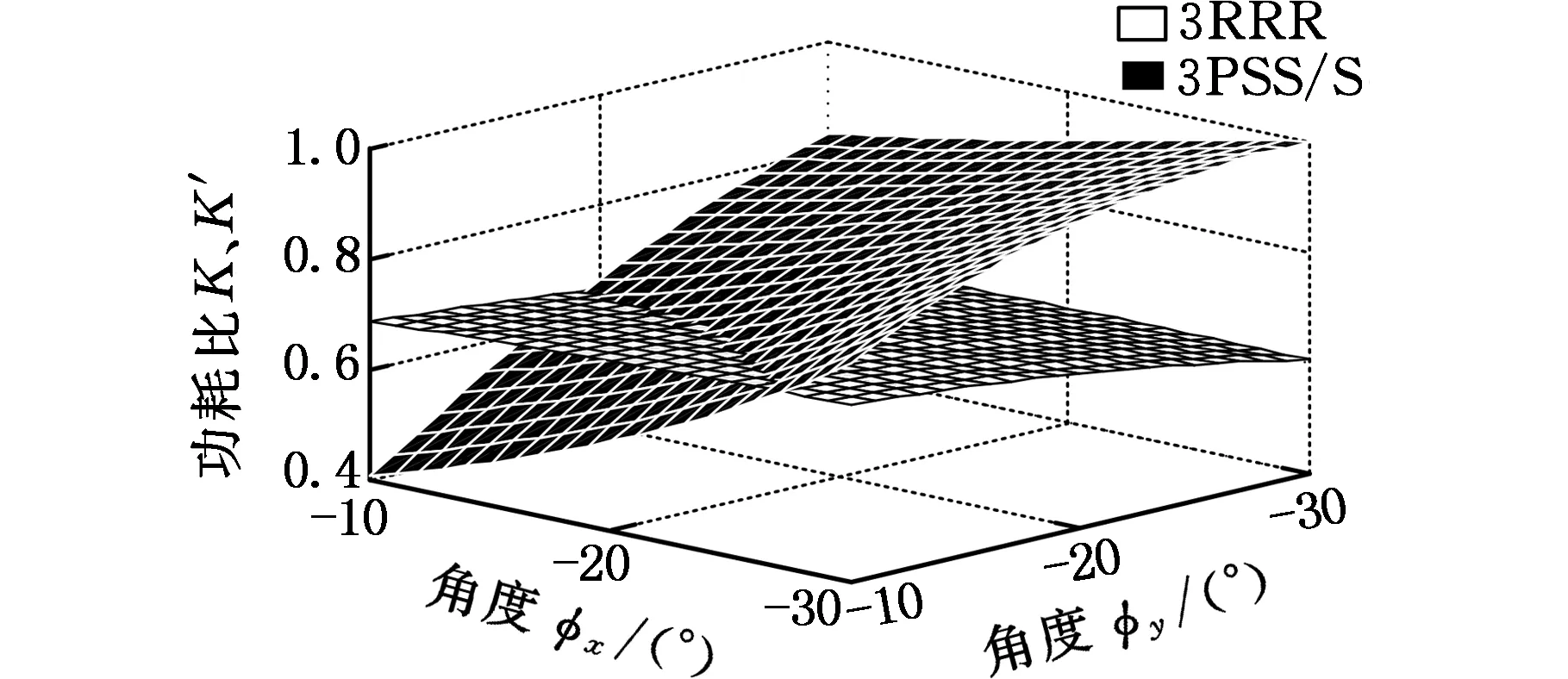
(c)φz=-30°图4 动平台逆向转动时3PSS/S与3RRR机构功耗比对比Fig.4 Power consumption ratio comparison between 3PSS/S and 3RRR mechanism when the moving platform rotates in the backward direction

3PSS/S平均功耗比K13RRR平均功耗比K2差值绝对值δϕx,ϕy∈[-30°,-10°]ϕz=-10°0.62360.66480.0412ϕz=-20°0.69410.66490.0292ϕz=-30°0.77660.66490.1117ϕx,ϕy∈[10°,30°]ϕz=10°0.51510.48970.0254ϕz=20°0.49500.52090.0295ϕz=30°0.47190.59160.1197功耗比均值0.59600.59950.0035

在输入端，通过控制系统反馈伺服电机力矩T1、T2、T3以及驱动角速度ω1、ω2、ω3，可得输入瞬时功率表达式为

Pi=|T1ω1|+|T2ω2|+|T3ω3|

(9)

图5 3PSS/S并联肩关节样机功耗比实验系统Fig.5 Power consumption ratio experimental system of 3PSS/S parallel mechanism

在输出端，利用陀螺仪测量动平台绕固定坐标轴x、y、z的转动角度φx、φy、φz。为确保测量数据的连续性，陀螺仪采用每秒100次的测量频率，将所得数据导入MATLAB中进行曲线拟合，得φx、φy、φz的拟合函数分别为

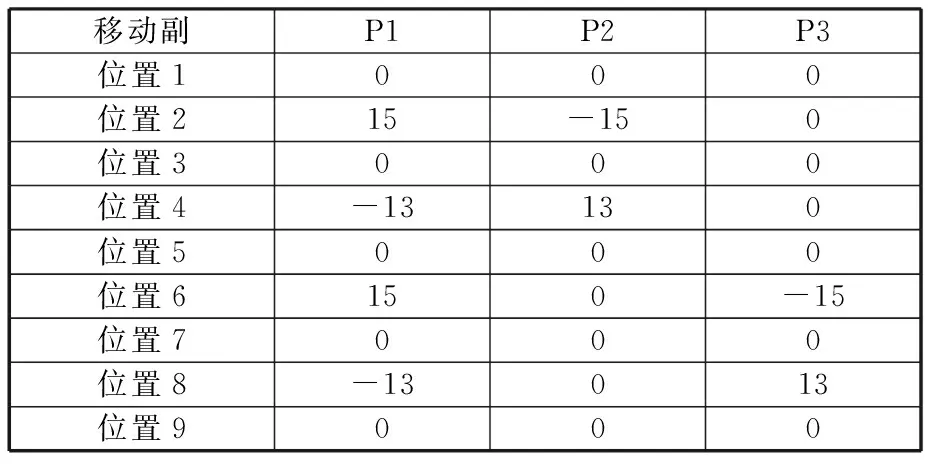
表3 移动副运动轨迹点

(a)位置2 (b)位置4

(c)位置6 (d)位置8图6 不同换向位置时3PSS/S并联样机姿态示意图Fig.6 Posture diagram of 3PSS/S parallel prototype in different commutation position

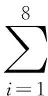
(10)

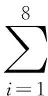
(11)

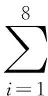
(12)

进而可得动平台角度变化曲线,如图7所示。

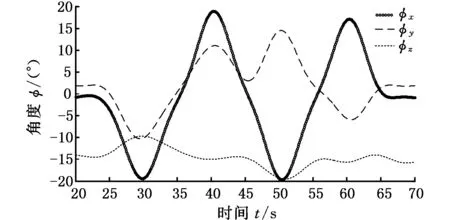
图7 3PSS/S并联机构动平台角度变化曲线Fig.7 Angle curves of the moving platform of 3PSS/S parallel mechanism

将所得拟合函数对时间求一阶导数，得动平台绕x、y、z各轴的角速度拟合函数:

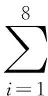
(13)

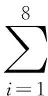
(14)

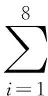
(15)

进而绘制得到机构动平台角速度变化曲线,如图8所示。

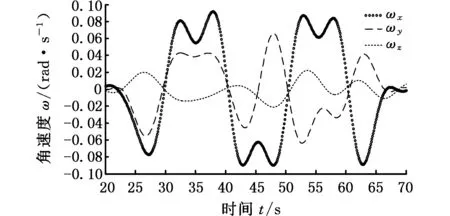
图8 3PSS/S并联机构动平台角速度变化曲线Fig.8 Angular velocity curves of the moving platform of 3PSS/S parallel mechanism

将所得拟合函数对时间求二阶导数，得动平台绕x、y、z各轴的角加速度拟合函数:

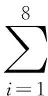
(16)

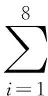
(17)

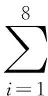
(18)

进而可得机构动平台角加速度变化曲线,如图9所示。

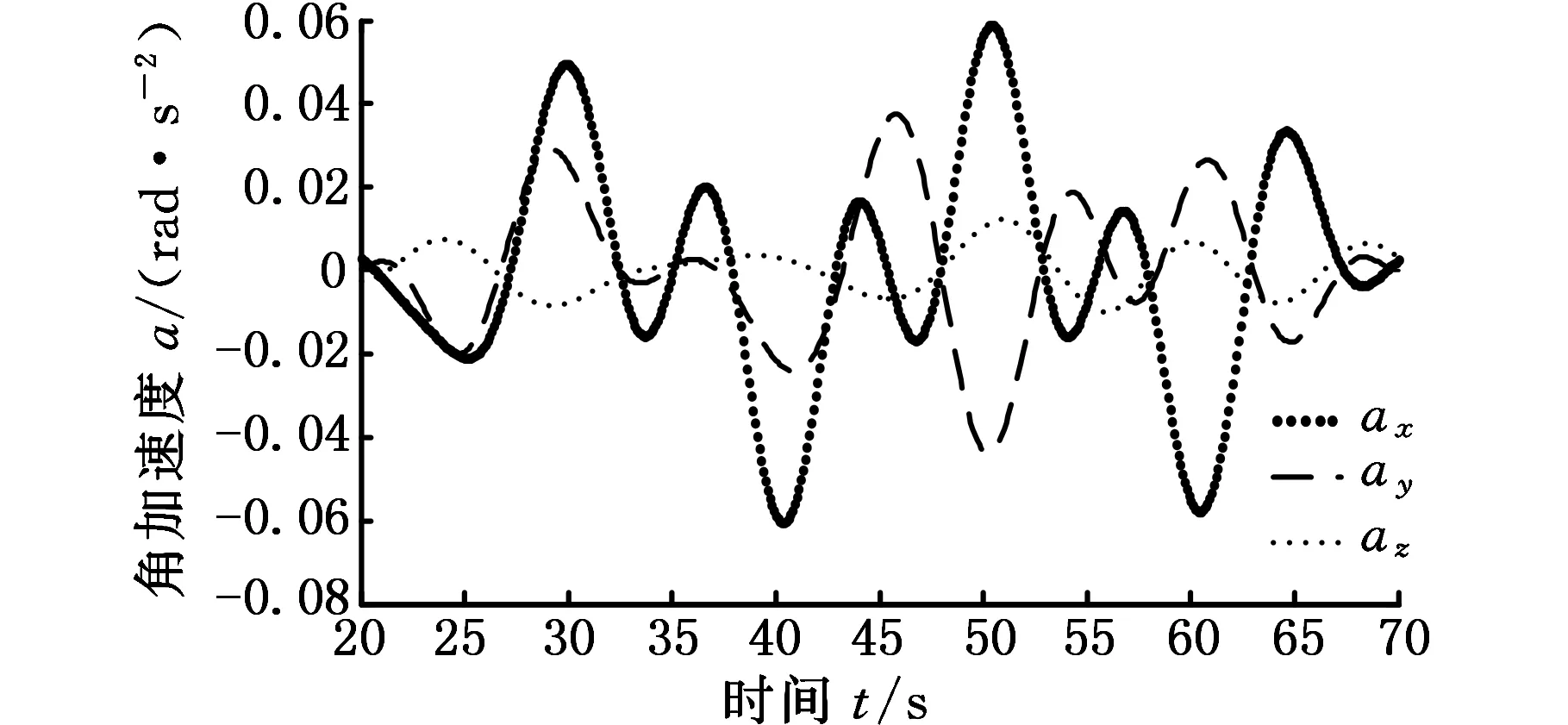
图9 3PSS/S并联机构动平台角加速度变化曲线Fig.9 Angular acceleration curves of the moving platform of 3PSS/S parallel mechanism

前述所得3PSS/S并联机构动平台角度、角速度以及角加速度拟合函数中，各参数值如表4所示。

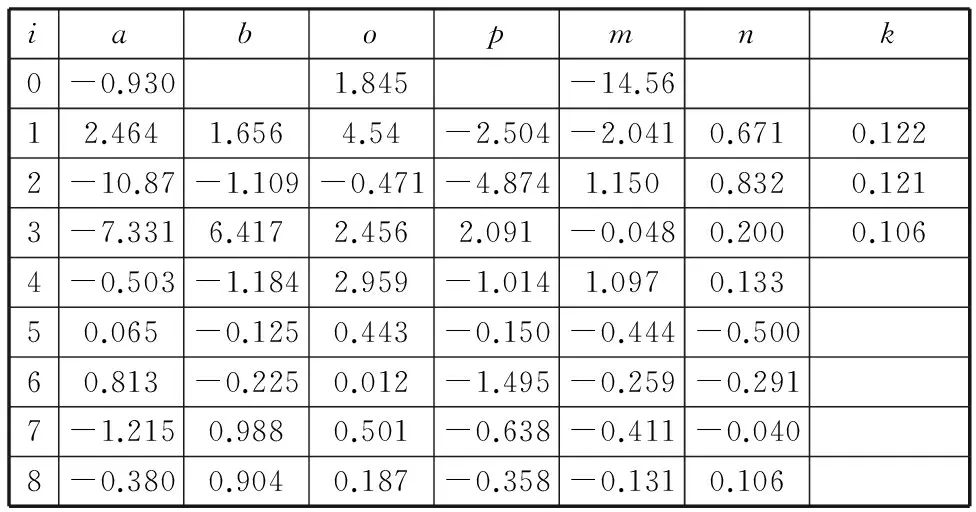
表4 3PSS/S并联机构动平台运动拟合函数参数Tab.4 Motion fitting function parameters of the moving platform of 3PSS/S parallel mechanism

设定Jx、Jy、Jz为负载分别在x、y、z三轴方向上产生的转动惯量，其表达式分别为

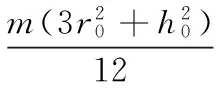
(19)

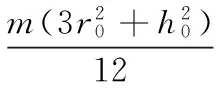
(20)

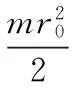
(21)

式中，m为圆柱状负载质量;r0为负载半径;h0为负载高度。

负载绕各轴转动惯量与其绕对应轴角加速度的乘积，即为负载作用于动平台的广义力矩沿各轴方向的分量，则广义力矩沿各轴分量表达式为

Mx=Jxax

(22)

My=Jyay

(23)

Mz=Jzaz

(24)

结合式(3)，可得输出端总瞬时输出功率表达式为

Po=Jxaxωx+Jyayωy+Jzazωz

(25)

根据式(5)、式(9)、式(25)计算可得3PSS/S并联机构实验功耗比，并结合MATLAB曲线拟合功能，求到期望轨迹下实验功耗比曲线,如图10所示。

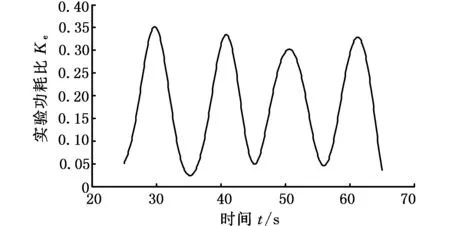
图10 3PSS/S并联机构实验功耗比拟合曲线Fig.10 Fitting curve of experimental power consumption ratio of 3PSS/S parallel mechanism

将所得负载绕x、y、z轴的角度、角速度拟合函数代入式(1)中，可得机构理论输入速度，将式(22)～式(24)所得的广义力矩代入式(2)中，可得机构理论输入力矩，根据式(3)～式(5)功耗比理论计算模型，可得到理论功耗比曲线,如图11所示。

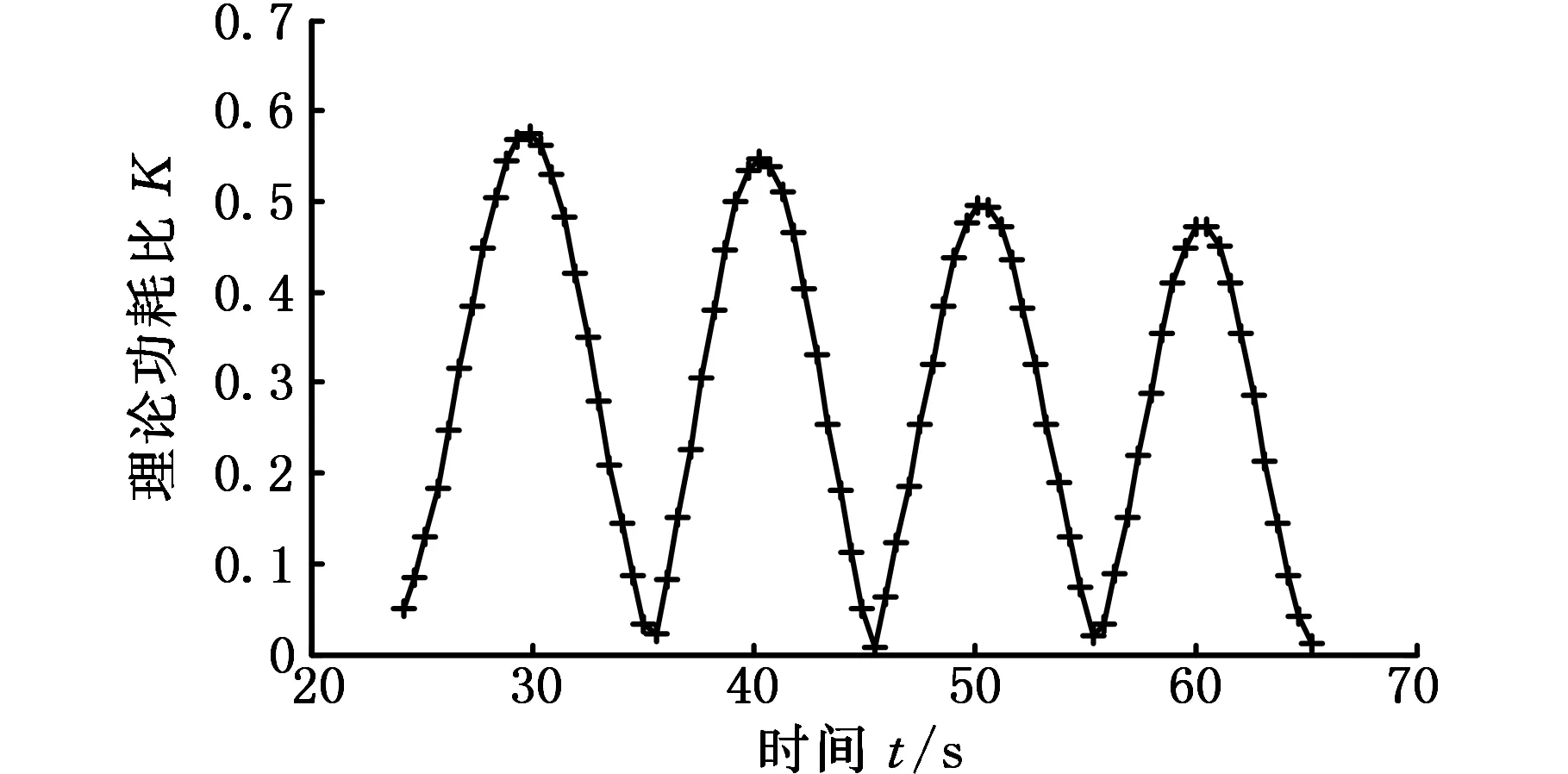
图11 3PSS/S并联机构理论功耗比曲线图Fig.11 Fitting curve of theoretical power consumption ratio of 3PSS/S parallel mechanism

选取不同时间点理论与实验功耗比数据进行对比，如表5所示。

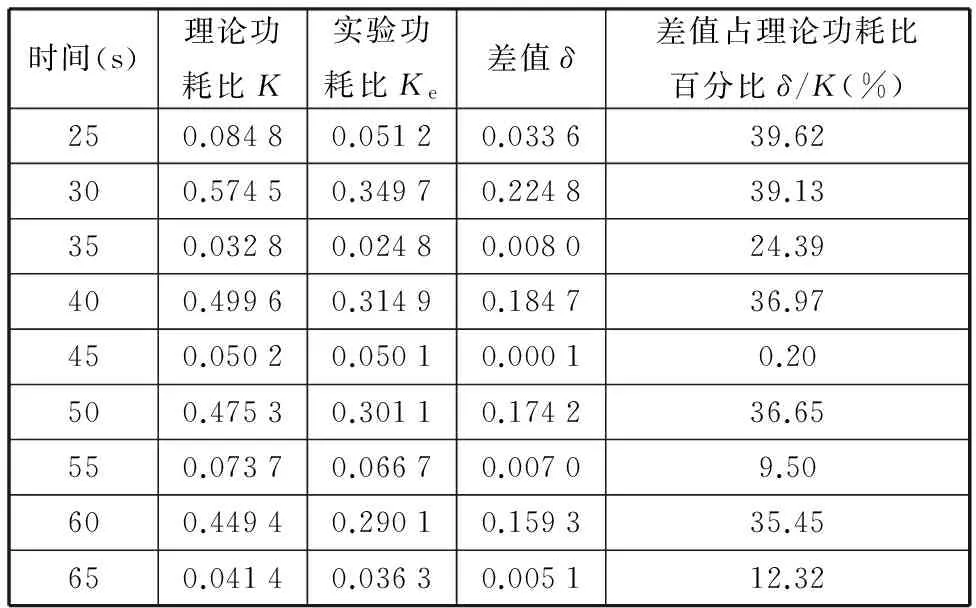
表5 3PSS/S并联机构理论与实验功耗比数值对比

由表5可见，总体而言功耗比实验数值低于理论计算数据，且个别点差值还较大。究其原因，一方面本文中的功耗比性能指标基于机构本体进行分析，研究重心在于机构功耗比指标及不同构型间的比较，因此理论模型中暂未考虑因样机构件的重力、惯性力等而消耗的能量。此外，所研制实验样机运动副较多，运动关节间总是存在一定间隙，而间隙的存在会导致碰撞而产生能量损失；同时，运动副的摩擦力作用也会产生能耗。对比图10与图11可见，在相同运动轨迹下，实验所得数据与理论值变化趋势大体相同，一定程度上验证了功耗比指标模型的有效性。

4 结论

(1)基于机构输入端与输出端的实际功耗，提出功耗比性能指标，可为关节仿生机构优化设计提供指导；对比3PSS/S和3RRR两种球面并联机构在既定工况和轨迹下的功耗比数值，结果表明两种机构的功耗传递性能大致相当。

(2)完成3PSS/S并联肩关节样机功耗比实验，比较其实验所得功耗比与理论模型计算功耗比，两者变化趋势相同，验证了功耗比计算模型的合理性，可为并联式肩关节工程研制中的能耗预估提供参考。

[1] YI B J, FREEMAN R A, TESAR D. Force and Stiffness Transmission in a Redundantly Actuated Mechanism: the Case for a Spherical Shoulder Mechanism[J]. ASME, Design Engineering Divison (Publication)DE,1992,45:163-172.

[2] 苑飞虎, 赵铁石, 赵延治, 等. 并联机构承载能力分析[J]. 中国机械工程,2015,26(7):871-877.

YUAN Feihu, ZHAO Tieshi, ZHAO Yanzhi, et al. Analysis of Load Carrying Capacity of Parallel Mechanism[J]. China Mechanical Engineering,2015,26(7):871-877.

[3] KORAYEM M H, BAMDAD M. Dynamic Load-carrying Capacity of Cable-suspended Parallel Manipulators[J]. The International Journal of Advanced Manufacturing Technology,2009,44(7/8):829-840.

[4] KORAYEM M H, BAMDAD M, TOURAJIZADEH A, et al. Analytical Design of Optimal Trajectory with Dynamic Load-carrying Capacity for Cable-suspended Manipulator[J]. The International Journal of Advanced Manufacturing Technology,2012,60:317-327.

[5] TSAI M J, LEE H W. Generalized Evaluation for the Transmission Performance of Mechanisms[J]. Mechanism and Machine Theory,1994,29(4):607-618.

[6] CHANG W T, LIN C C, LEE J J. Force Transmissibility Performance of Parallel Manipulators[J]. Journal of Robotics System,2003,20(11):659-670.

[7] WANG J S, WU C, LIU X J. Performance Evaluation of Parallel Manipulators：Motion/Force Transmissibility and Its Index[J]. Mechanism and Machine Theory,2010,45(10):1462-1476.

[8] LIU X J, WU C, XIE F. Motion/Force Transmission Indices of Parallel Manipulators[J]. Frontiers of Mechanical Engineering,2011,6(1):89-91.

[9] 陈祥, 谢富贵, 刘辛军. 并联机构中运动/力传递功率最大值的评价[J]. 机械工程学报,2014,50(3):1-9.

CHEN Xiang, XIE Fugui, LIU Xinjun. Evaluation of the Maximum Value of Motion/Force Transmission Power in Parallel Manipulators[J]. Chinese Journal of Mechanical Engineering,2014,50(3):1-9.

[10] WU C, LIU X J, WANG L. Optimal Design of Spherical 5R Parallel Manipulators Considering the Motion/Force Transmissibility[J]. Journal of Mechanical Design,2010,132(3):031002.

[11] YOSHIKAWA T. Manipulability of Robotic Mechanisms[J]. The International Journal of Robotics Research,1985,4(2):3-9.

[12] YOSHIKAWA T. Dynamic Manipulability of Robot Manipulators[J]. Journal of Robotic Systems,1985,2(1):113-124.

[13] 季晔, 刘宏昭, 原大宁, 等. 一种四自由度并联机构的性能指标分析[J]. 中国机械工程,2012,23(3):258-263.

JI Ye, LIU Hongzhao, YUAN Daning, et al. Analyses for Performance Indices of a Four-DOF Parallel Manipulator[J]. China Mechanical Engineering,2012,23(3):258-263.

[14] 周玉林, 刘磊, 高峰. 3自由度球面并联机构3-RRR静力全解[J]. 机械工程学报,2008,44(6):169-176.

ZHOU Yulin, LIU Lei, GAO Feng. Static Full-solutions of Spherical Parallel Mechanism 3-RRR with 3-DOF[J]. Journal of Mechanical Engineering,2008,44(6):169-176.

[15] HOU Y L, HU X Z, ZENG D X, et al. Biomimetic Shoulder Complex Based on 3-PSS/S Spherical Parallel Mechanism[J]. Chinese Journal of Mechanical Engineering,2014,28(1):29-37.

[16] HOU Y L, LI Z S,WANG Y, et al. Mechanics Unloading Analysis and Experimentation of a New Type of Parallel Biomimetic Shoulder Complex[J]. Chinese Journal of Mechnaical Engineering,2016,29(4):649-658.