基于响应面模型的白车身多目标轻量化设计

王震虎 周巧英 刘开勇 方向东 李落星

1.湖南大学汽车车身先进设计制造国家重点实验室，长沙,4100822.湖南大学机械与运载工程学院，长沙,4100823.重庆长安汽车欧尚研究院，重庆,400023

0 引言

目前，实现车身轻量化的主要途径为采用高强度轻质新材料,减薄车身部件的壁厚和以车身质量最小为目标、以车身刚度和模态性能为约束条件的单目标优化设计[2]。然而，将白车身结构的刚度、模态和强度等性能指标只作为约束条件，待优化结果出来后再进行验算，这样得到的轻量化结果并非最优解。近年来，同时考虑车身减重与结构性能的多目标优化方法越来越受到重视[3-5]。

本文基于经试验验证后的白车身有限元模型，选取正负灵敏度较高的部件壁厚作为设计变量，采用一阶响应面方法建立白车身质量、弯扭刚度、一阶弯扭模态的近似模型。以白车身质量最小和扭转刚度最大为优化目标函数，弯曲刚度和一阶弯扭模态为约束条件，采用非支配排序遗传算法进行多目标的轻量化设计。

1 白车身基础性能仿真分析及试验验证

对某MPV车型白车身采用薄板单元QUAD4和TRIA3进行网格划分，网格大小为8 mm。焊点采用RBE2和ACM单元模拟。模型材料采用钢材，弹性模量E=210 GPa，泊松比υ=0.3，密度ρ=7.9×103kg/m3。整个白车身的网格节点数共792 898个，壳单元792 515 个，其中三角形单元占单元总数的3.24%，焊点单元6 934个。白车身弯扭刚度和自由模态分析采用MSC/NASTRAN软件进行求解。

1.1 弯扭刚度分析

白车身结构静态刚度包括弯曲刚度和扭转刚度。弯曲刚度主要用来评价承受乘员质量或货物质量时抵抗变形的能力；扭转刚度用来评价车身在不平的路面上抵抗扭转变形的能力。

1.1.1弯曲刚度分析

约束左后减振器安装支座孔中心点123自由度，右后减振器支座安装孔中心点13自由度，左前减振器安装支座孔中心点23自由度，右前减振器安装支座孔中心点3自由度。加载点位置位于前悬架弹簧和后减振器接附点且垂直于纵梁位置，左右加载力大小都为1 kN，方向为Z轴负方向(图1)。分析完成后，位移的测点为载荷作用线的延长线与车架纵梁的交点，弯曲刚度计算公式为

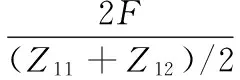
(1)

式中，F为加载力，F=2000 N；Z11、Z12分别为左右测量点的Z向位移的绝对值，mm。

仿真分析得到白车身弯曲刚度的位移分布，如图2所示。提取白车身两侧加载点的Z向位移，分别为0.239 mm和0.237 mm，将位移代入式(1)可得弯曲刚度，为8 403 N/mm。

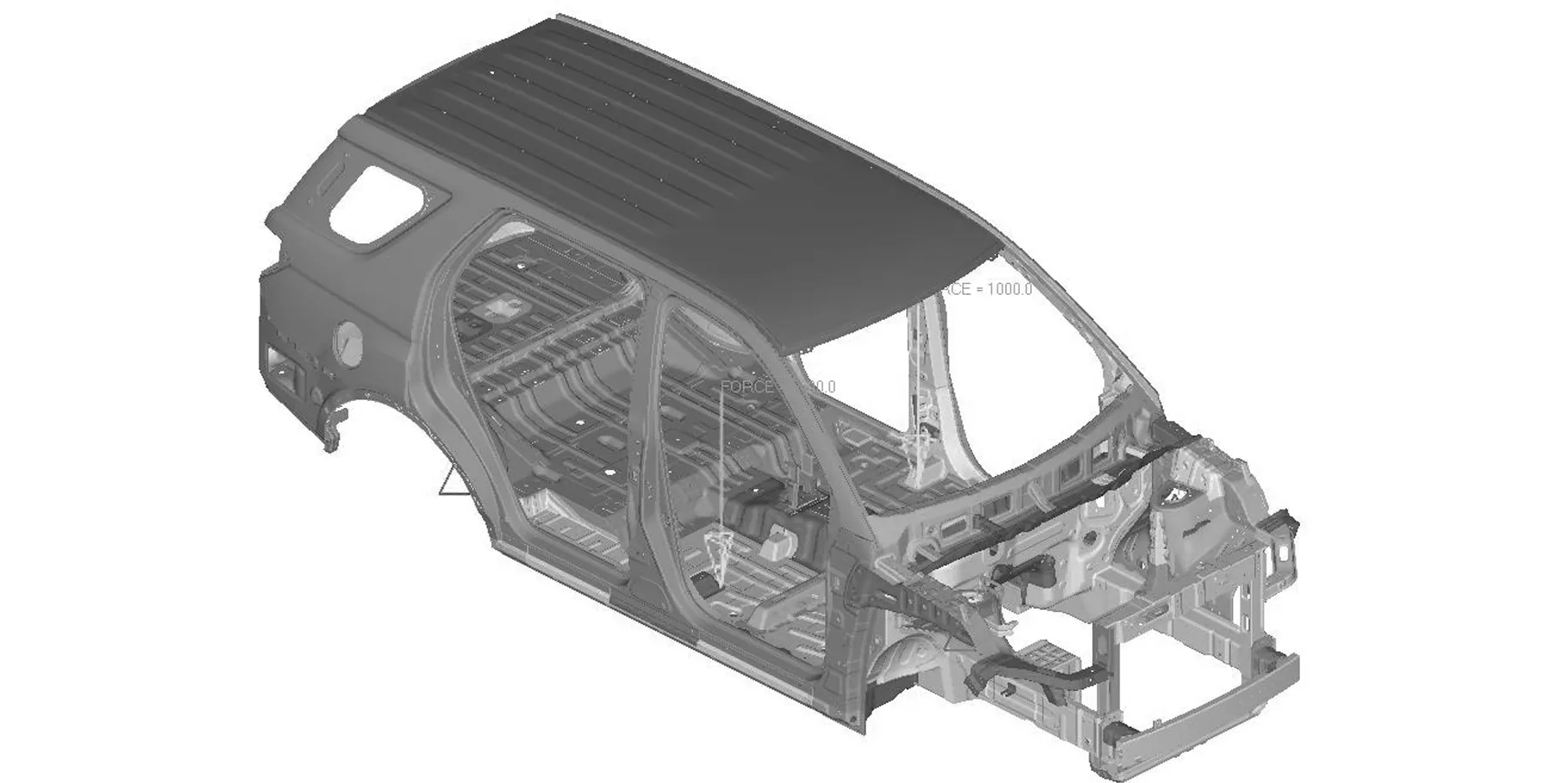
图1 白车身弯曲刚度仿真模型Fig.1 Bending stiffness simulation model of body in white

图2 白车身弯曲刚度位移云图Fig.2 Bending stiffness displacement distribution of body in white

1.1.2扭转刚度分析

约束左后减振器安装支座安装孔中心点123自由度，减振器安装支座安装孔中心点13自由度。在前减振器安装孔中心施加多点约束(MPC)：Zl+Zr=0(Z1、Zr分别为左右两侧前减振器安装孔中心点的位移)，在左右减振器支座安装孔中心点之间施加2 000 N·m的扭矩作用，等效于在Z向施加3 710 N的力(图3)。分析完成后，位移测量点为两加载点连线垂直投影与纵梁底面交线的中点1、2，以及右后减振器安装支座安装孔中心点连线垂直投影与纵梁底面交线的中点3、4，代入下式可求出扭转刚度：

Kt=2 000/[(Z21+Z22)/L12-(Z23+Z24)/
L34] (N·m/rad)

(2)

式中，Z21、Z22、Z23、Z24分别为测量点Z向位移的绝对值,mm；L12、L34分别为测量点1、2和测量点3、4的距离，L12=785 mm，L34=1024.9 mm。

图3 白车身扭转刚度仿真模型Fig.3 Torsion stiffness simulation model of body in white

图4 白车身扭转刚度位移云图Fig.4 Torsion stiffness displacement distributionof body in white

仿真分析得到白车身扭转刚度的位移分布，如图4所示。提取4个测量点的位移分别为：Z21=0.963 2 mm，Z22=0.956 3 mm，Z23=0.005 56 mm，Z24=0.009 958 mm。利用式(2)，求得扭转刚度大小为844 618 N·m/rad。

1.2 自由模态分析

汽车在实际行驶过程中，会在各种振动源的激励下产生振动。当振动源激励的频率和车身的固有频率接近时，车身会产生较大幅度的振动，对汽车的舒适性和可靠性造成非常大的影响[6]。振动源的大部分激励都集中在较低的频率范围，因而需要评估白车身的低阶固有频率，特别是一阶弯曲频率和一阶扭转频率。

本文采用计算效率高的兰索斯(Lanczos)法计算白车身的各阶模态和振型。分析过程中不添加任何约束，分析频率下限设为1 Hz，范围为1～70 Hz，从而避免计算前6阶刚体模态，节省仿真时间。计算结束后，得出白车身的一阶扭转模态为38.09 Hz(图5)，一阶弯曲模态为44.59 Hz(图6)。

图5 白车身一阶扭转模态云图Fig.5 1st-order torsion model displacement distribution of body in white

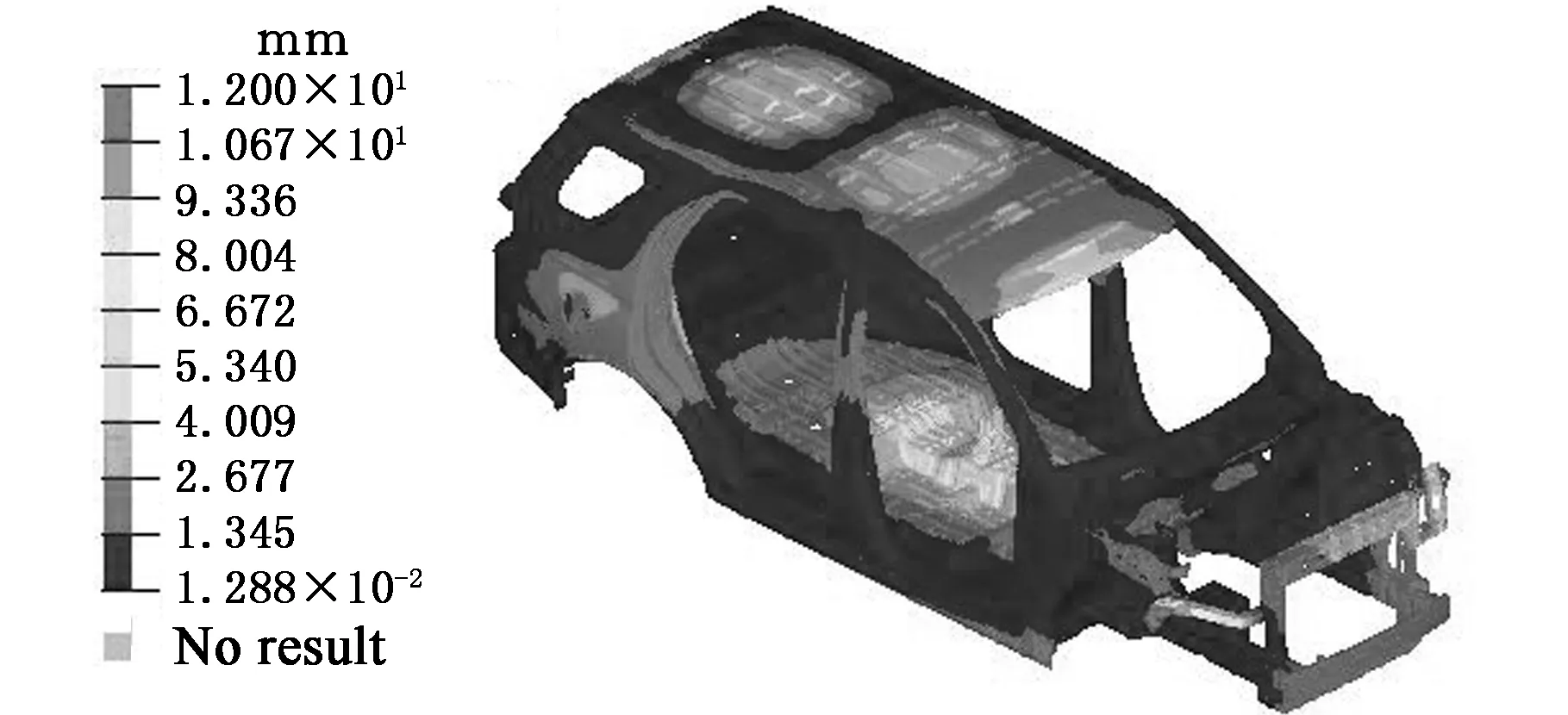
图6 白车身一阶弯曲模态云图Fig.6 1st-order bending model displacement distribution of body in white

1.3 试验验证

本节开展静刚度和模态试验以验证白车身有限元模型的正确性。弯曲刚度试验时，将车身放置在试验台架上，用夹具约束前后悬架的连接点，在白车身前排座椅后安装横梁处进行加载，载荷大小为2 000 N。试验测点和模拟分析测点大致相同，并利用百分表测量测点的垂直位移。弯曲刚度试验测试现场见图7。扭转刚度试验时，用夹具约束后悬架弹簧与车身连接处，在前悬架处通过千斤顶施加2 000 N·m扭矩。试验测点和模拟分析测点大致相同，并利用百分表测量测点变形情况。扭转刚度试验测试现场见图8。

图7 白车身弯曲刚度试验测试现场Fig.7 Testing picture of bending stiffness of body in white

图8 白车身扭转刚度试验测试现场Fig.8 Testing picture of torsion stiffness of body in white

图9是白车身模态试验测试现场。模态试验中将白车身前舱和背门安装处与橡胶绳连接，分别在右前悬架安装处以及左后悬架弹簧安装处施加激励，右前悬架处的激励点向后倾斜45°，左后悬架弹簧处激励点垂直向上，这样有利于同时激励出横向、纵向以及垂向模态，采用力学传感器采集激振力信号。图10是白车身上均匀布置的167个加速度传感器测点示意图，构成的轮廓可以表现出车身的几何形状。

图9 白车身模态试验测试现场Fig.9 Testing picture of mode of body in white

图10 白车身模态试验测点布置Fig.10 Layout of measuring points in body in white model test

表1为白车身弯扭刚度、一阶弯扭模态试验与仿真结果对比。由表1可知，弯曲刚度和扭转刚度的误差分别为6.90%和5.95%，一阶扭转模态和一阶弯曲模态的误差分别为4.41%和1.32%。4种性能指标仿真和试验结果基本接近，仿真误差都小于7%，表明本文建立的白车身有限元模型是准确的。

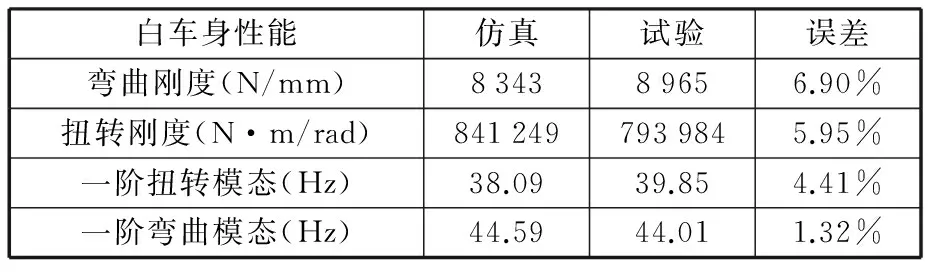
表1 车身基础性能试验和仿真结果对比

2 相对灵敏度分析

灵敏度分析可用来研究结构性能参数对结构设计参数变化的敏感性，灵敏度的数值反映了设计变量对响应性能的影响[7]。灵敏度函数

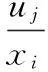
(3)

对于一个线性结构，其动力学方程为

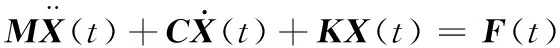
(4)

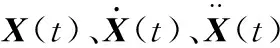
无阻尼结构自由振动的特征方程为

(5)

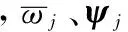
固有频率对设计变量的灵敏度可以通过对式(5)的第一项设计变量求偏导获得：

(6)

求解式(6)得固有频率的灵敏度：

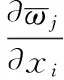
(7)

求解式(7)得刚度的灵敏度：

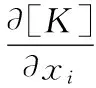
(8)

式中，K为矩阵K中的元素;Δxi为厚度变化量。

传统采用商业软件计算的灵敏度为车身性能对板件壁厚的灵敏度，然而车身各个零部件的形状和面积各异，增加相同厚度时，各零部件的质量增加也各有差异，因此，在进行轻量化设计特别是壁厚优化时，单纯地通过壁厚灵敏度并不能直观地看出质量对车身性能的影响。本文采用弯扭刚度灵敏度和模态灵敏度分别除以质量灵敏度，从而获得车身刚度性能相对板件质量的灵敏度，即

(9)

式中，Sb、St、Sf、Sw分别为弯曲刚度灵敏度、扭转刚度灵敏度、模态灵敏度和质量灵敏度；Rb、Rt、Rf分别为相应的相对灵敏度。

从某种意义上说，相对灵敏度就是零件壁厚增大后，单位质量增加所带来的目标响应的性能提升。刚度的相对灵敏度结果均为正值，说明增大壁厚或质量能使刚度值增大，而模态的相对灵敏度有正有负，说明壁厚或质量增大不一定会使模态增大。

根据相对灵敏度分析结果，筛选出了19个部件进行壁厚优化，这19个部件对车身刚度性能提升相对较大，或对减重贡献较大，且优化后对汽车的碰撞性能影响较小，所筛选的部件如表2所示，在白车身上所处位置如图11所示。

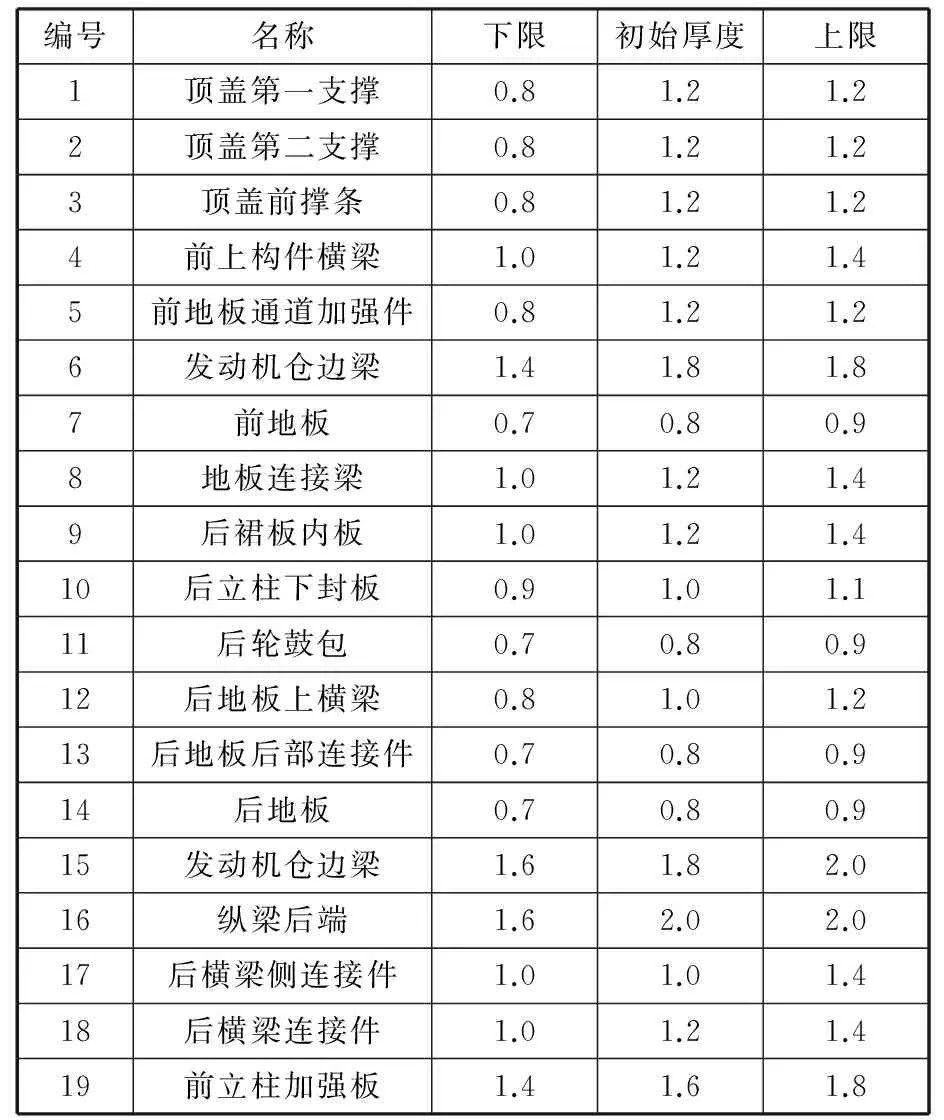
表2 白车身优化部件

图11 白车身优化部件Fig.11 The components of dimensional optimization of body in white

3 多目标轻量化设计

3.1 拉丁超立方试验设计

试验设计的目的主要是为了获取样本点，以便通过样本点来建立近似模型。常用的试验设计方法包括全因子设计、部分因子设计、正交数组设计、拉丁超立方设计、最优拉丁超立方设计等。拉丁超立方试验设计方法的空间填充能力强，每个因素的设计空间都被均匀划分，所有因素都具有相同数目的分区，每一个因素的每个水平只被研究一次，能用较少的样本点来研究较多的因子。图12是两因素全因子与拉丁超立方试验设计采样对比。本文采用拉丁超立方试验设计方法对需要优化的19个设计变量采样，拉丁超立方试验次数设置为100。

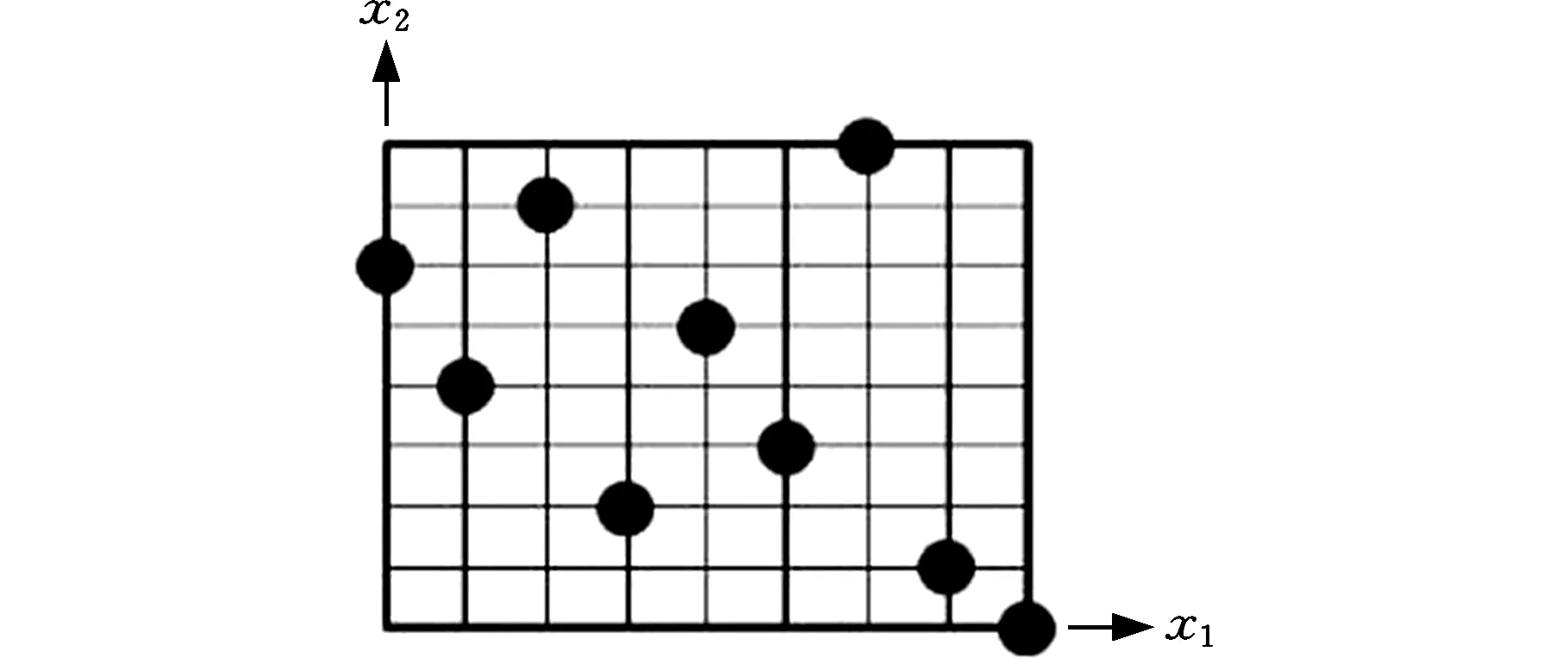
(b)拉丁超立方试验设计图12 两因素试验设计采样对比Fig.12 The contrast of two factor test sampling

3.2 响应面近似模型

多项式响应面近似模型采用不同阶次的多项式来近似表达响应目标与设计变量之间的函数关系，是一种回归模型，具有数学表达式简单、收敛速度快、计算量小等特点[6]。

考虑设计变量交互作用的多项式响应面近似模型为

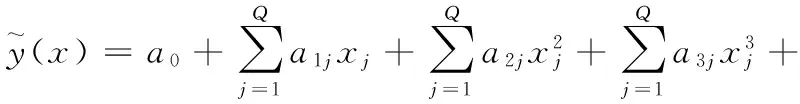
(10)

式中，a为多项式系数；xj为设计变量；Q为设计变量个数。

本文所采用的响应面近似模型为一阶响应面模型，根据前面采集的拉丁超立方样本点数据，建立符合计算要求的计算模型。本文采用复相关系数R2来表征近似模型的逼近程度，其定义为

R2=1-Qc/Qz

(11)

式中，Qc为残余偏差平方和；Qz为偏差平方和。

由于所涉及的优化变量共有19个，故构建一阶响应面模型所需要的最少样本点数量为20个。本文用拉丁超立方方法所采集的样本数共100个，超出的样本数可用来提高近似模型的精度。由式(11)可知，R2越接近1.0，模型的精度越高。白车身质量、弯扭刚度、一阶弯扭模态的响应面模型的拟合精度如图13所示，复相关系数如表3所示。由图13和表3可知，该响应面模型的5个性能指标的R2都非常接近于1.0，因此该近似模型可代替真实模型计算。

3.3 基于遗传算法的多目标轻量化设计

由于本文研究的白车身其扭转刚度性能相比其他同类车型较低，因此，多目标轻量化设计以白车身质量最小、扭转刚度最大作为优化目标。本文以白车身弯曲刚度和一阶弯曲模态以及一阶扭转模态作为约束，其中，约束的值不小于初始值的95%，将19个零部件的壁厚作为设计变量，得到多目标优化的数学模型：

minm

maxKT

s.t.KB≥8 000 N/mm

fB≥40 Hz

fT≥35 Hz

采用第二代非支配排序遗传算法(NSGA-Ⅱ)[8]对上述模型进行迭代寻优。本文种群规模设置为16，最大代数为40，交叉率为0.9，一共进行了640次的迭代。计算得到的白车身零件优化非劣解前沿如图14所示。

本文轻量化设计的目的在于减小白车身质量的同时，使得白车身的刚度性能不会损失过多。由图14可知，在质量为363.3 kg处，扭转刚度出现了一个扭转刚度跨度非常大的拐点，这个拐点发生在优化过程的第556步，该拐点的值既能很好地达到轻量化效果，又能保证白车身扭转刚度性能损失较小，故而本文选取该拐点的值作为轻量化设计的最优解。

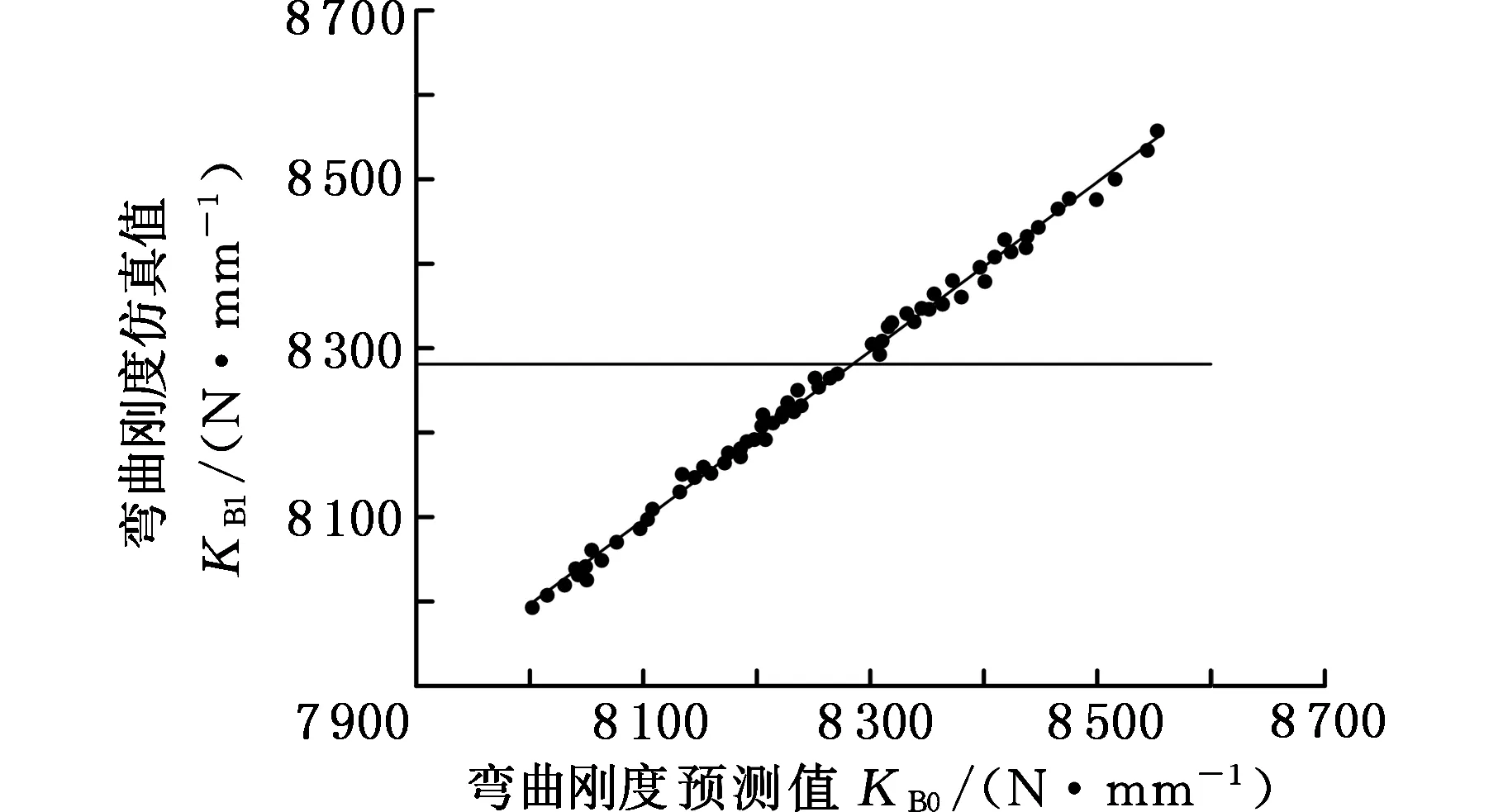
(a)弯曲刚度模型

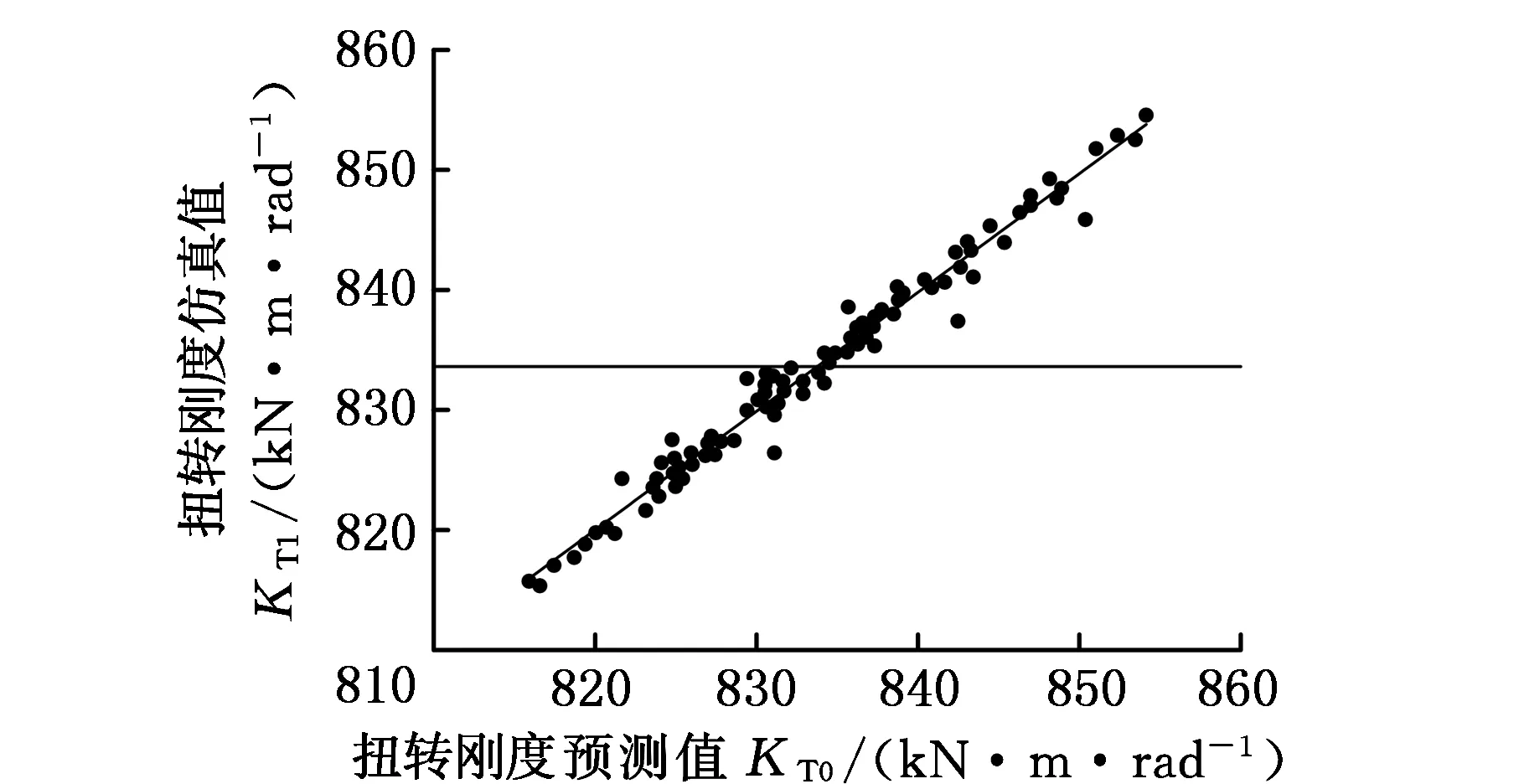
(b)扭转刚度模型

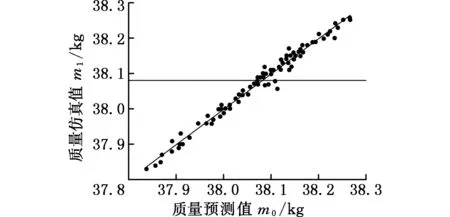
(c)质量模型

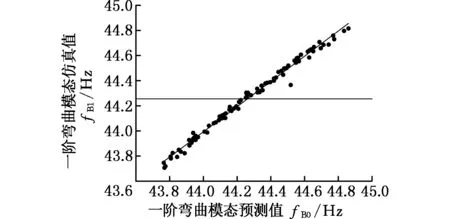
(d)一阶弯曲模态模型

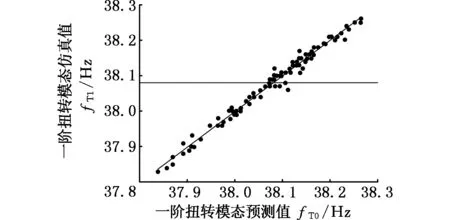
(e)一阶扭转模态模型图13 白车身5种性能指标近似模型的预测值与仿真值对比Fig.13 The comparison of predicted and simulated values for five performance parameters approximate models in body in white

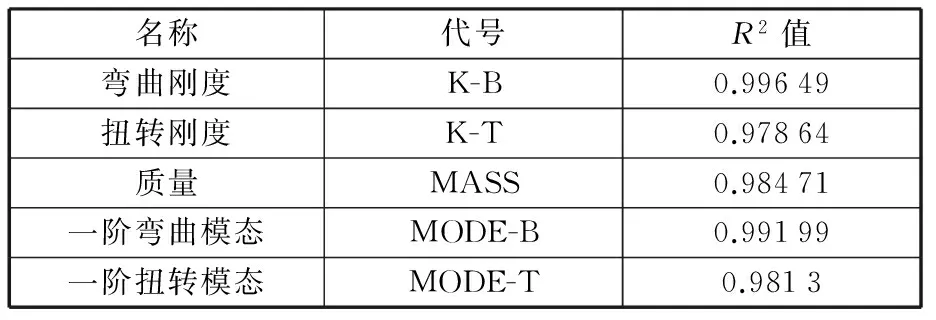
名称代号R2值弯曲刚度K-B0.99649扭转刚度K-T0.97864质量MASS0.98471一阶弯曲模态MODE-B0.99199一阶扭转模态MODE-T0.9813

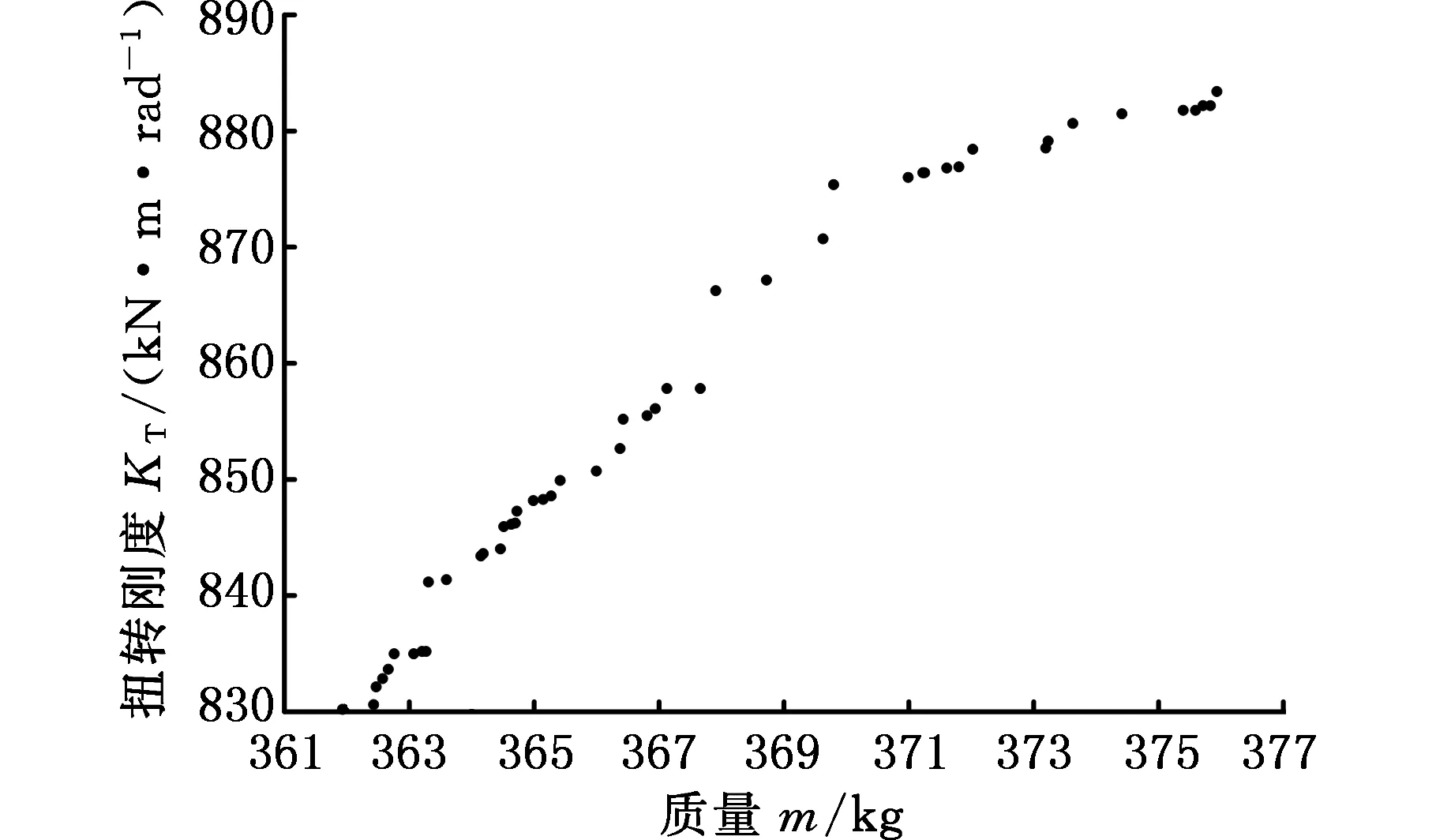
图14 白车身轻量化设计变量的非劣解前沿Fig.14 The front non inferiority solution of lightweight optimization design variable

优化前后，白车身19个设计变量的壁厚变化如表4所示，白车身的基础性能变化如表5所示。由表4可知，经过多目标优化以后，白车身质量减小6.4 kg，其中顶盖第一撑条、顶盖第二撑条、顶盖前撑条、前上构件横梁、前地板通道加强件、发动机舱边梁、前地板、后裙板内板和D立柱上角内板的壁厚优化后都减小，说明这些部件对基础性能的影响较小，能在基本不影响基础性能的基础上实现轻量化设计；而后轮鼓包、后横梁侧连接件和后横梁连接件壁厚增大，说明这些部件对基础性能的影响较大，它们也位于白车身受力的关键部位，应该加强处理。由表5可知，多目标轻量化设计后白车身弯曲刚度仅下降51N/mm，扭转刚度下降78 N·m/rad，一阶扭转模态增大0.19 Hz，一阶弯曲模态减小0.22 Hz，总的来说，白车身基础性能的变化比例控制在1.0%以内，说明白车身多目标轻量化设计能在不改变车身用材的前提下，很好地实现白车身质量的大幅度减小。

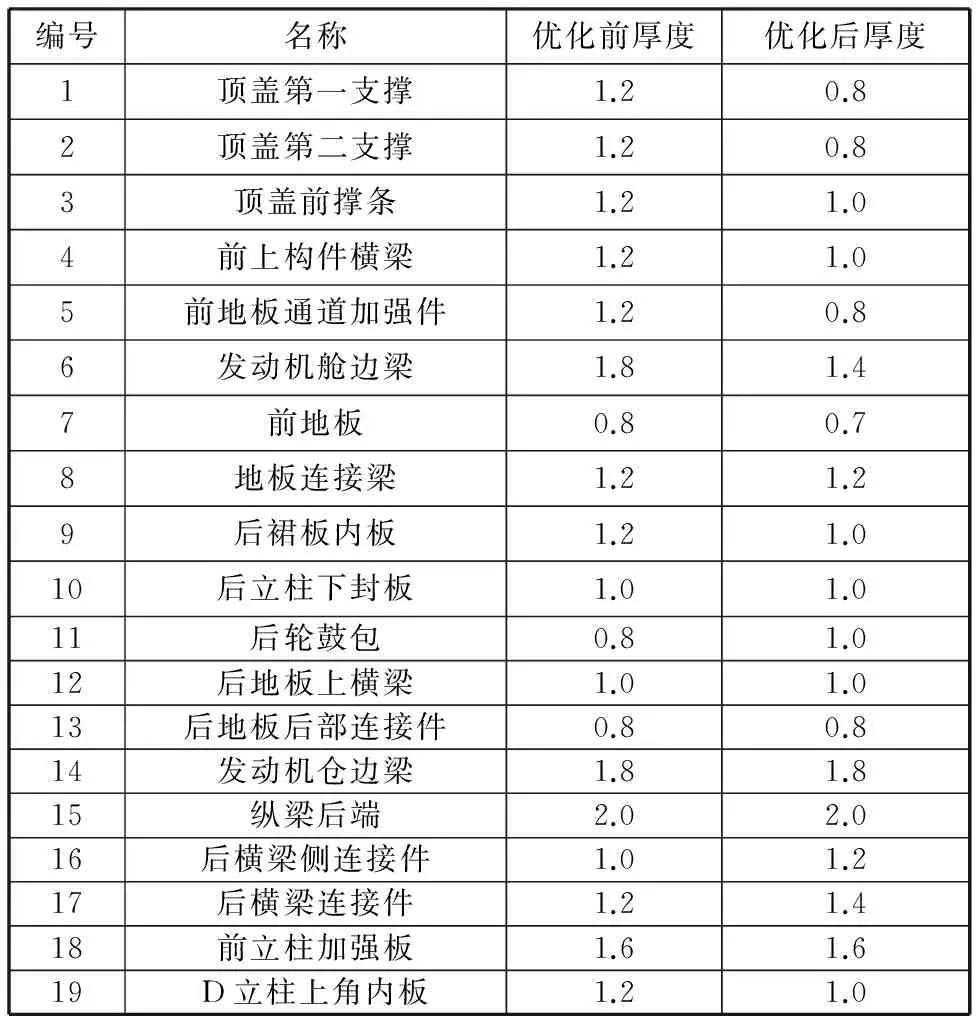
表4 多目标优化前后车身零部件的壁厚

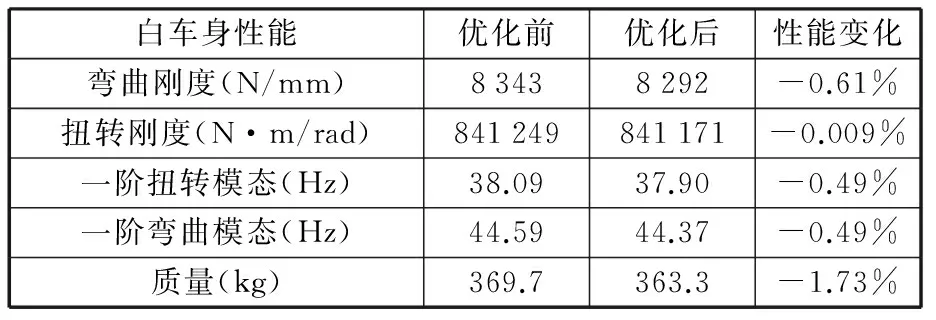
表5 白车身优化前后性能对比Tab.5 The performance comparison of body in white before and after optimization

4 结论

(1)文中建立的某MPV车型白车身有限元模型精度较高，白车身弯扭刚度、一阶弯扭模态仿真与试验结果的误差分别为6.9%、5.95%和1.32%、4.41%。

(2)利用相对灵敏度分析方法选取了19个白车身零部件壁厚作为轻量化设计变量；采用拉丁超立方试验方法和一阶响应面模型方法建立白车身质量、弯扭刚度、一阶弯扭模态的近似模型，模型的复相关系数R2都接近于1.0，模型精度高。

(3)以白车身质量最小和扭转刚度最大为优化目标函数，弯曲刚度和一阶弯扭模态为约束条件，采用非支配排序遗传算法对白车身进行多目标轻量化设计，使得白车身基础性能变化均小于1%，而且在不改变用材的前提下，实现白车身减重6.4 kg。

[1] 刘志文, 李落星. 轻量化构件弯曲短流程工艺研究现状与进展[J]. 中国有色金属学报,2014,24(8):2003-2012.

LIU Zhiwen, LI LuoXing. Review of Bending Short Process for Lightweight Component[J]. Chinese Journal of Nonferrous Metals,2014,24(8):2003-2012.

[2] 韩旭, 朱平, 余海东,等. 基于刚度和模态性能的轿车车身轻量化研究[J]. 汽车工程,2007,29(7):545-549.

HAN Xu, ZHU Ping, YU Haidong, et al. A Study on the Weight-reduction of Car-body with Required Stiffness and Modal Performances[J]. Automotive Engineering,2007,29(7):545-549.

[3] 王传青. 白车身前端结构-材料-性能一体化轻量化多目标协同优化设计[D]. 长春：吉林大学,2016.

WANG Chuanqing. Structure-material-performance Integration Lightweight Multi-objective Collaborative Optimization Design for Front Structure of BIW[D]. Changchun: Jilin University,2016.

[4] 杜倩倩, 陆善彬. 基于网格变形技术的车身改型多目标优化[J]. 合肥工业大学学报:自然科学版,2016,39(8):1031-1036.

DU Qianqian, LU Shanbin. Multi-objective Optimization of Car Body Modification Based on Mesh Deformation[J]. Journal of Hefei University of Technology(Natural Science),2016,39(8):1031-1036.

[5] 张勇，李光耀，王建华.多目标遗传算法在整车轻量化优化设计中的应用研究[J]. 中国机械工程,2009,20(4):500-503.

ZHANG Yong, LI Guangyao, WANG Jianhua. Design Optimization on Lightweight of Full Vehicle Based on Multi-objective Genetic Algorithm[J].China Mechanical Engineering,2009,20(4):500-503.

[6] JACKSON E D, HOLMÉN B A. Modal Analysis of Vehicle Operation and Particulate Emissions from Connecticut Transit Buses[J]. Transportation Research Record Journal of the Transportation Research Board,2009,2123(2123):76-87.

[7] 张辉, 张晓静, 刘志文, 等. 横梁接头形式优化及其在白车身性能提升上的应用[J]. 湖南大学学报:自然科学版,2017,44(4):1-8.

ZHANG Hui, ZHANG Xiaojing, LIU Zhiwen, et al. Form Optimization of Crossbeam Joints and Its Application in Performance Improvement of Body in White[J]. Journal of Hunan University of Natural Science,2017,44(4):1-8.

[8] 谢然, 兰凤崇, 陈吉清, 等. 满足可靠性要求的轻量化车身结构多目标优化方法[J]. 机械工程学报,2011,47(4):117-124.

XIE Ran, LAN Fengchong, CHEN Jiqing, et al. Multi-objective Optimization Method in Car-body Structure Light-weight Design with Reliability Requirement[J]. Journal of Mechanical Engineering,2011,47(4):117-124.