基于伪随机子集生成的Boolean函数

刘华宁,陈晓林

(西北大学数学学院,陕西西安 710127)

1 引言

Boolean函数在流密码,分组密码以及散列函数的研究中起着重要作用.为了研究Boolean函数,人们提出了许多有关Boolean函数的密码学指标.

设 F2是一个二元域,Fn2是 F2上的一个n维线性空间,所谓n元Boolean函数B(x1,···,xn)是指从 Fn2到 F2的一个映射. 设 x=(x1,···,xn),a=(a1,···,an)∈Fn2,则〈a,x〉=a1x1+···+anxn表示通常的内积.Boolean 函数B(x1,···,xn)的最大 Fourier系数 ^B(a)定义为

Boolean函数B(x1,···,xn)的非线性定义如下

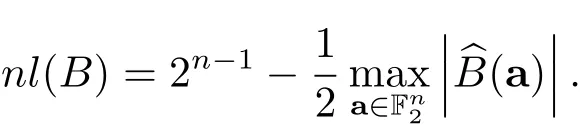
每一个Boolean函数都可以唯一地表示成多项式的形式,称为Boolean函数的代数正规型

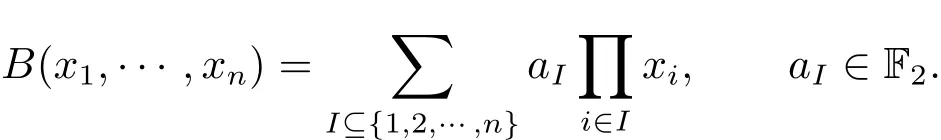
Boolean函数的稀疏性spr(B)是代数正规型中非零系数单项式的个数.此外Boolean函数的平均灵敏度σav(B)定义如下其中a(i)是a改变第i个坐标后所得的向量.

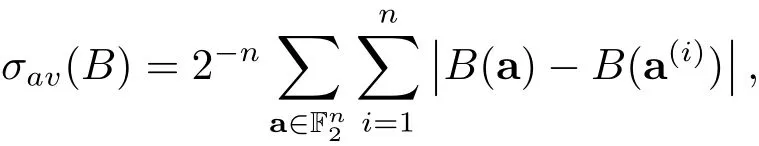
近几年来,一些密码学研究者从数论的角度出发构造了许多具有“好”的密码学性质的Boolean函数.例如,Coppersmith与Shparlinski[1]利用模p的二次剩余构造了如下的Boolean函数.

命题1.1 设p为奇素数,s=blog2pc,其中bxc表示不超过x的最大整数.定义Boolean函数为

其中uj∈{0,1}且1≤j≤s.则有

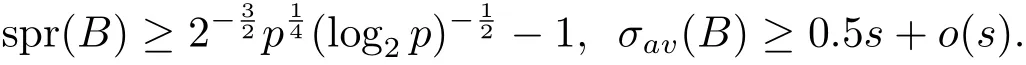
Lange与Winterhof[2]将上述命题进行了推广.

命题1.2 设p为奇素数,Fq是阶为q=pr(r≥1)的有限域,β0,···,βr−1是Fq在Fp上的一组基,s=blog2pc.定义Boolean函数如下

其中ki−1=ui1+ui2·2+···+uis·2s−1,uij∈{0,1}且 1≤j≤s,1≤i≤r.则有

随后文献[3]进一步研究了命题1.2中Boolean函数的性质,得到了以下结果.

命题1.3 设p,r,s,B如以上命题所定义.则有

最近几十年来,随着数论、组合以及相关学科的发展,伪随机子集得到了深入的研究和广泛的应用.许多论文都是关于这一领域的,这些论文中提出了大量的思想、方法和工具.1992年,Chung与Graham[4]发现整数环的子集具有一类令人惊奇的互相等价的性质,并且如果一个子集满足这类性质中的任何一条,则满足其余性质.Gowers[5]对整数环的伪随机子集进行了具体的数量分析,利用所定义的Gowers范数,在整数环的子集引入了新的伪随机测度,进而给出了Szemer´edi定理的新证明.

伪随机子集不仅有着深刻的理论意义,还在网络安全、密码学等领域中具有广泛的应用.研究者发现伪随机子集可以提高密钥预分配过程的效率和安全性,进而改善密钥管理、广播认证协议、无线传感网络的过程(参阅文献[6]),另外还可用于构造匿名路径以避免路径信息被窃听(参阅文献[7]与[8]).

本文将利用伪随机子集构造大族的Boolean函数,并在第2节到第4节中证明下面的结论.

定理1.1 设p为奇素数,q=pr,Fq为有限域,A⊂Fq是Fq的子集,满足

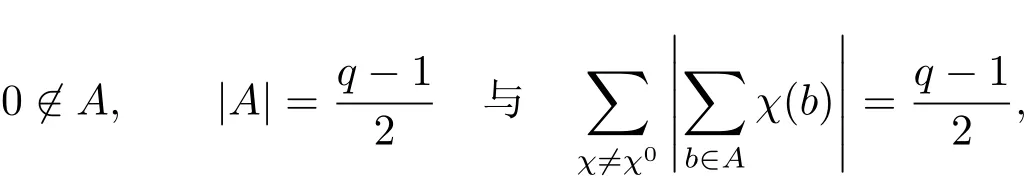
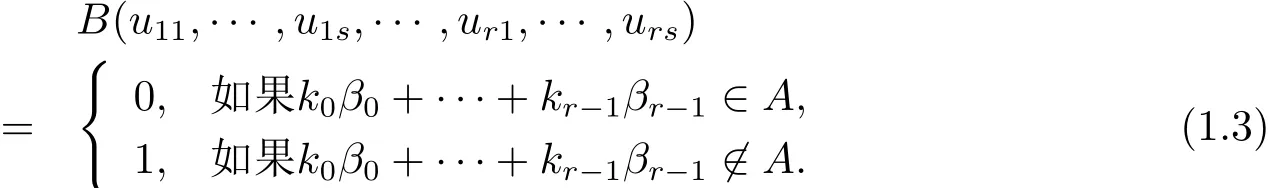
则有

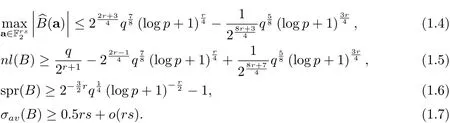
注 设p为奇素数,q=pr,Fq为有限域.定义不难证明

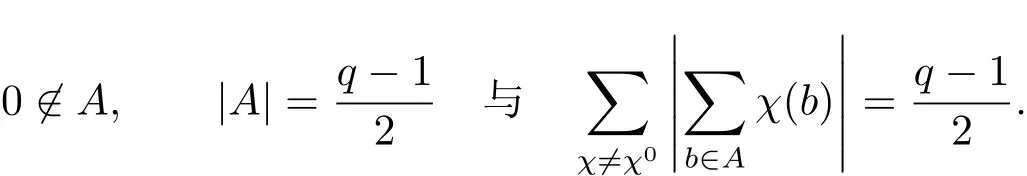
因此本文是对文献[2]与[3]的推广.

2 最大Fourier系数与非线性

首先介绍下面的引理.

引理2.1设p为奇素数,q=pn,χ为有限域 Fq上的d(d＞1)阶乘法特征,v1,···,vn是Fq在Fp上的一组基.设f(x)∈Fq[x]不能表为Fq上任何多项式的d次幂的常数倍,且在它的分裂域中有m个不同的根.定义

其中t1,···,tn是非负整数且t1＜p,···,tn＜p.则有

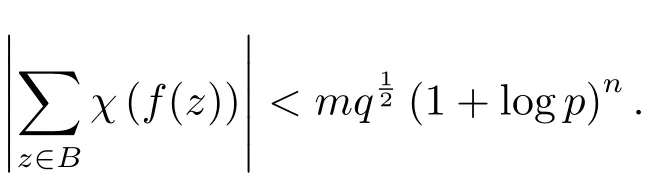
证 参阅文献[9]中的定理2.

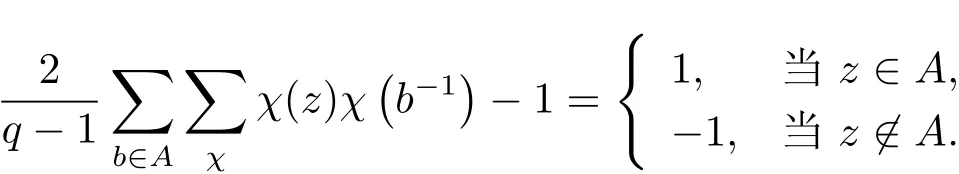
记ki−1=ui1+ui2·2+···+uis·2s−1,其中uij∈{0,1},1≤j≤s,1≤i≤r.定义

其中z=k0β0+···+kr−1βr−1,ki−1=ui1+ui2·2+···+uis·2s−1,1≤i≤r,且

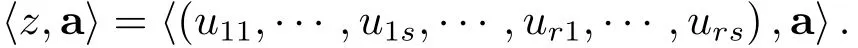
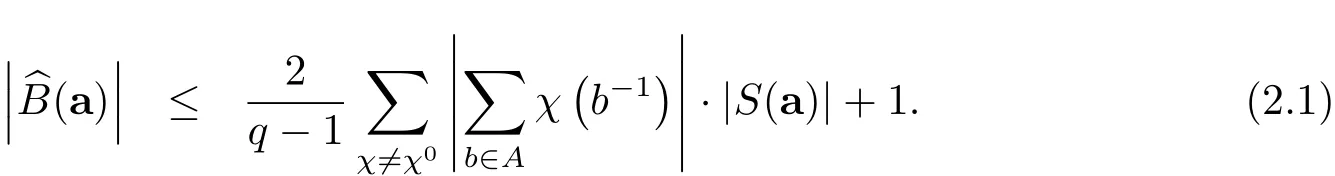
根据文献[3]中的方法,设x是一个整数且1＜x＜s,则有

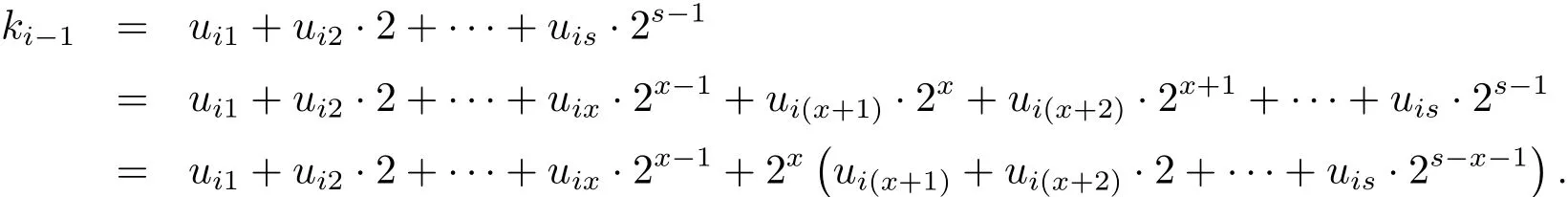
显然任意z∈H2s都能唯一地表为z=y+w,其中y∈H2x,且

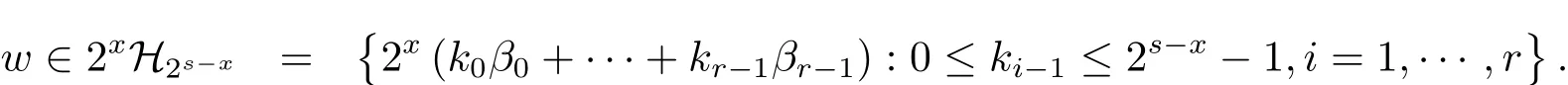
定义

易知〈z,a〉=〈y,b〉+〈w,c〉.由 Cauchy-Schwarz 不等式有

再由引理2.1可得

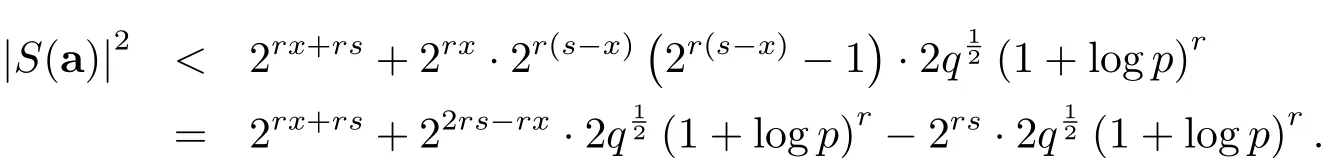
设实数x0满足

并取x=bx0c+1,有

结合(2.1)与(2.2)式可得

注意到

因此

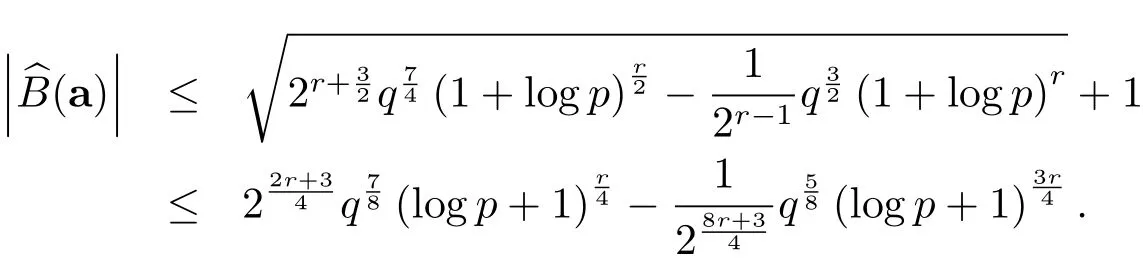
这就证明了(1.4)式.又由于s=blog2pc＞log2p−1,则有

从而可得(1.5)式.

3 稀疏性

设整数a满足2a＞(spr(B)+1)r1≥2a−1. 令M={0,···,2a−1}r{(0,···,0)},对每一个定义函数

其中mi=mi1+···+mia2a−1,mij∈{0,1},1≤j≤a,1≤i≤r. 对于定义在u11,···,u1(s−a),···,ur1,···,ur(s−a)的所有中,不同单项式的个数不超过spr(B).注意到|M|=2ar−1＞spr(B),则可以找到非平凡的线性组合,使得

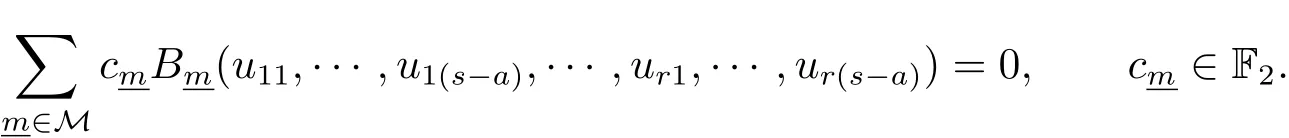
定义

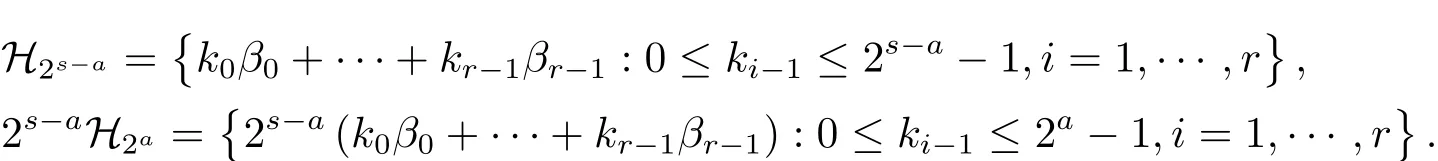
容易证明

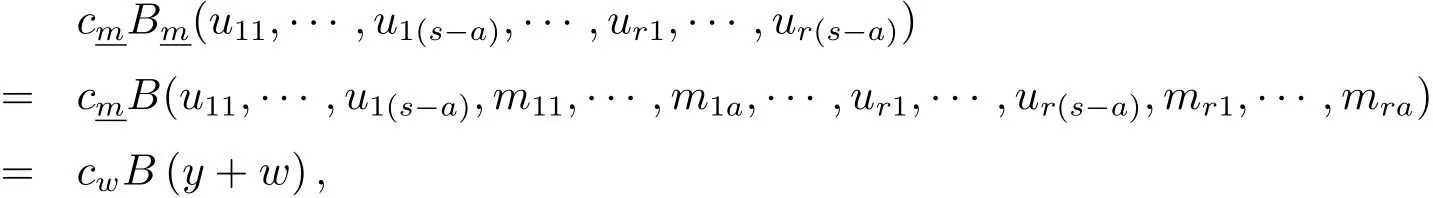
其中y∈H2s−a,w∈2s−aH2a{0},且与w∈2s−aH2a{0}是一一对应的.

定义

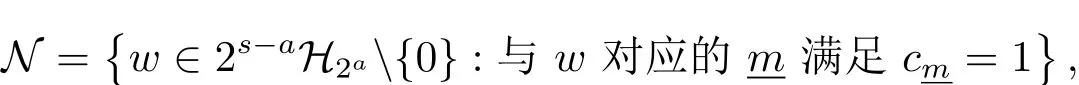
以及L=|N|.则有

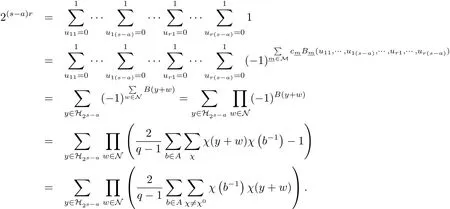
为方便起见,记N={w1,w2,···,wL}. 可得

设χ′是 Fq的乘法特征群的生成元,其阶为q−1,则可把χ1,···,χL分别写成

其中 1≤a1,···,aL≤q−2.定义

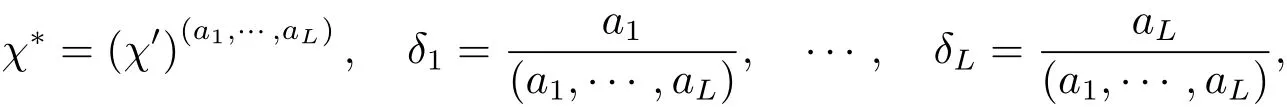
则χ∗的阶为q−1 的大于 1 的因数,1≤δ1,···,δL≤q−2,且 (δ1,···,δL)=1,从而

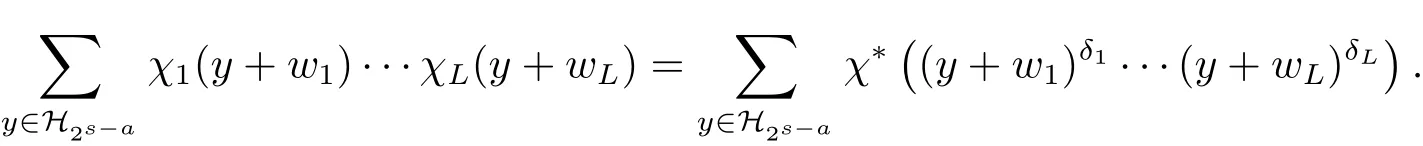
注意到w1,···,wL互不相同,且 (δ1,···,δL)=1. 则 (y+w1)δ1···(y+wL)δL不可能表

为某个多项式的d＞1次幂.由引理2.1可得

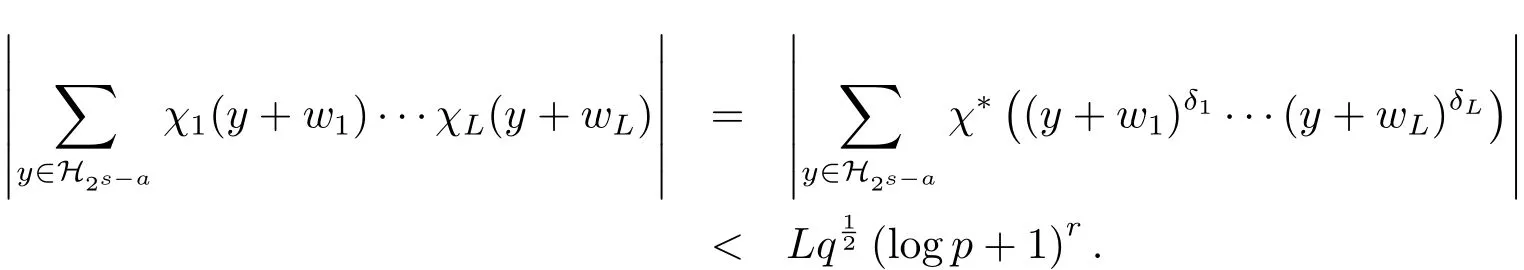
因此

注意到s=blog2pc＞log2p−1,有从而 spr(B)≥(2a−1)r−1＞这就证明了(1.6)式.

4 平均灵敏度

令

并记B′(k)=B(u11,···,u1s,···,ur1,···,urs),其中

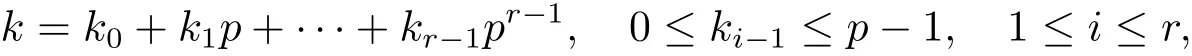
且

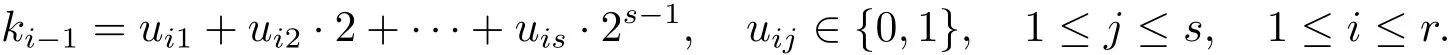
定义

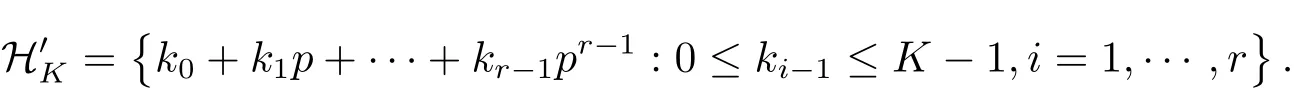
根据文献[3]中的方法,以及引理2.1可得

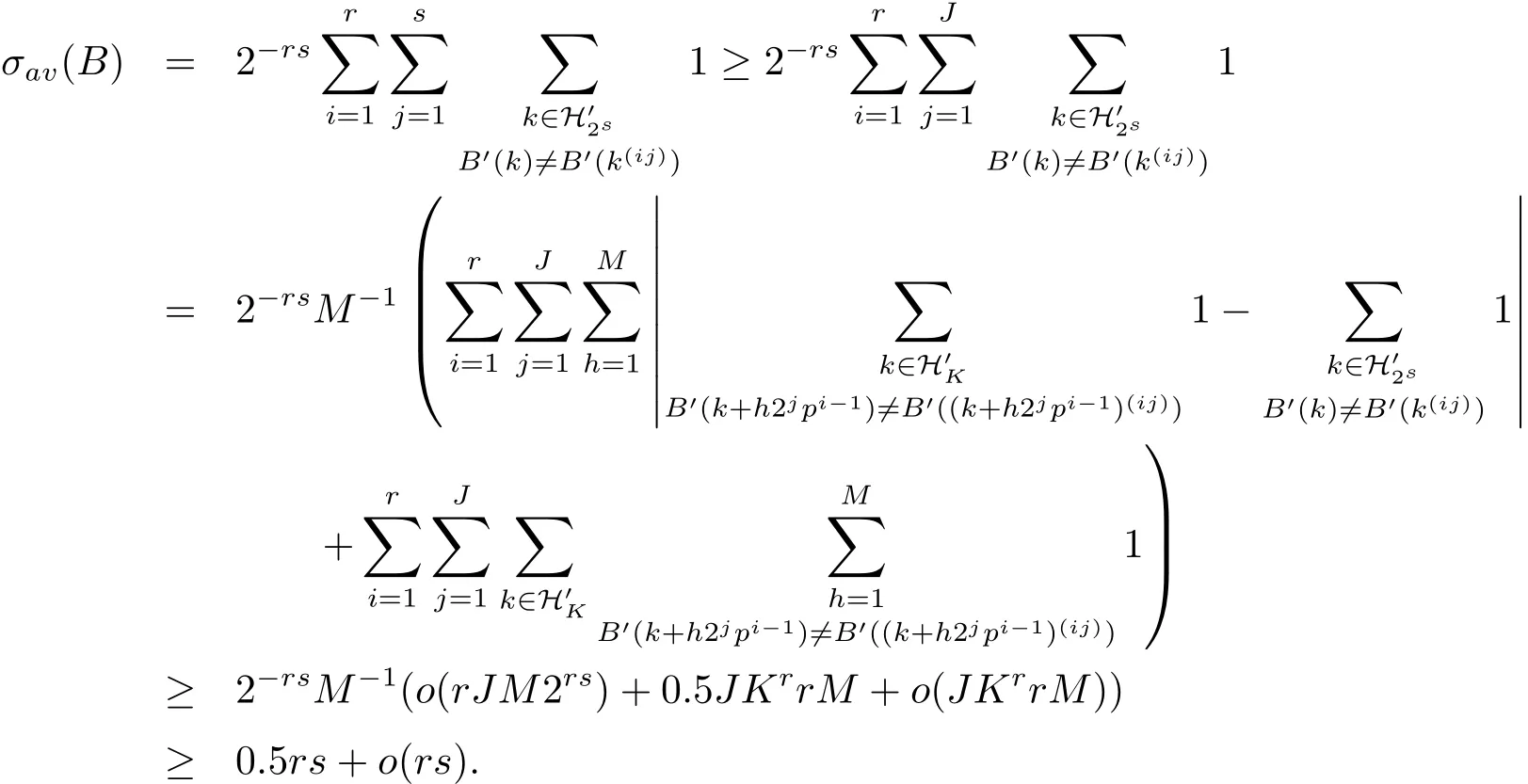
这就证明了(1.7)式.

5 进一步的讨论

利用相同的方法,还可构造范围更大的Boolean函数族,并证明下面的结论.

定理5.1 设p为奇素数,q=pr,Fq为有限域,A⊂Fq是Fq的子集,满足

设β0,···,βr−1是 Fq在 Fp上的一组基.定义s=blog2pc,并设uij∈{0,1},1≤j≤s,1≤i≤r.记ki−1=ui1+ui2·2+···+uis·2s−1,1≤i≤r.定义

则有

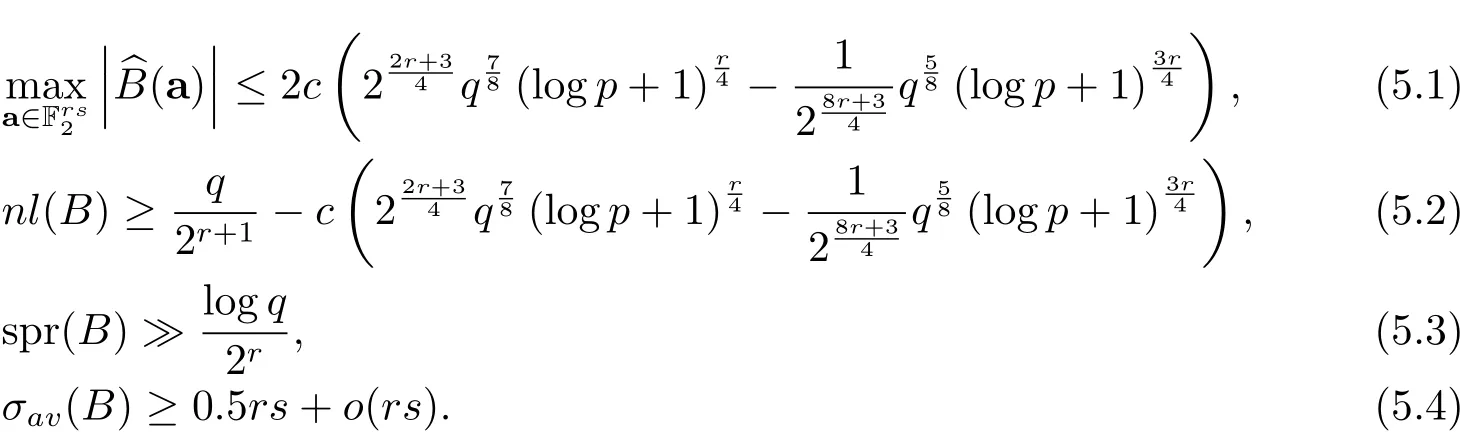
注 满足定理5.1中的条件的子集有很多个.例如,设g是F∗q的生成元,则下列子集

都满足定理5.1的要求.

[1]Coppersmith D,Shparlinski I E.On polynominal approximation of the discrete logarithm and the Diきe-Hellman mapping[J].J.Cryp.,2000,13(3):339–360.

[2]Lange T,Winterhof A.Incomplete character sums over finite fields and their application to the interpolation of the discrete logarithm by Boolean functions[J].Acta Arith.,2002,101(3):223–229.

[3]Lange T,Winterhof A.Interpolation of the discrete logarithm in Fqby Boolean functions and by polynomials in several variables modulo a divisor ofq−1[J].Disc.Appl.Math.,2003,128(1):193–206.

[4]Chung F R K,Graham R L.Quasi-random subsets of Zn[J].J.Combin.The.Ser.A,1992,61(1):64–86.

[5]Gowers W T.A new proof of Szemer´edi’s theorem[J].Geom.Funct.Anal.,2001,11(3):465–588.

[6]苏忠,林闯,任丰原.无线传感器网络中基于散列链的随机密钥预分发方案[J].计算机学报,2009,32(1):30–41.

[7]夏永波.Bent序列的构造及其相关值分布[J].数学杂志,2010,30(4):663–670.

[8]Xu L,Chen S,Huang X,Mu Y.Pseudonym and bloom filter based secure and anonymouse DSR protocol in wireless ad hoc network[J].Int.J.Comput.Netw.Commun.Secur.,2010,5(1):35–44.

[9]Winterhof A.Some estimates for character sums and applications[J].Des.Codes Cryptogr.,2001,22(2):123–131.