具有年龄结构随机种群系统数值解的渐近有界性

辛志贤张启敏李 强哈金才

(1.北方民族大学数学与信息科学学院,宁夏银川 750021)

(2.宁夏大学数学统计学院,宁夏银川 750021)

1 引言

随机微分方程被广泛应用于工程、生物、金融等领域[1−6],随机种群系统也引起了许多学者关注.本文研究如下具有年龄结构的随机种群系统模型[7]

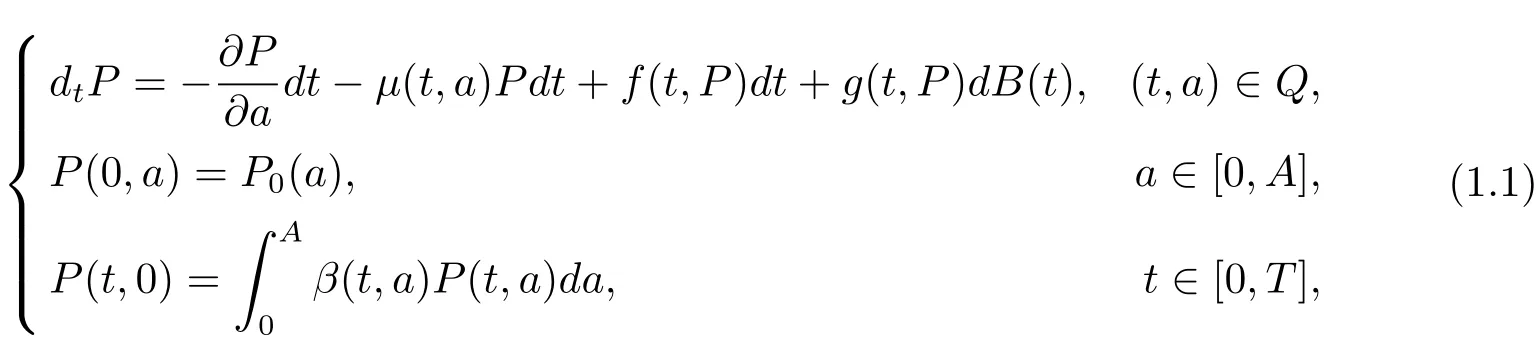
其中Q=(0,T)×(0,A),A是种群所能达到的最大年龄,表示t时刻年龄为a的种群密度;β(t,a)表示t时刻年龄为a的种群的出生率;µ(t,a)表示t时刻年龄为a的种群的死亡率;f(t,P)是外界环境的干扰,如迁移、地震、海啸等突发性灾害对种群的影响;g(t,P)dB(t)表示随机外界环境对系统的干扰;B(t)是定义在概率空间(Ω,Ft,P)上的Brown运动.

模型(1.1)考虑了随机环境对系统的扰动影响,更符合种群模型的实际意义.由于随机种群模型的解析解很难给出,因此数值解的计算显得尤为重要,并且在近几年,随机种群模型数值解的研究取得了很多成果.文献[8]研究了带跳的具有年龄结构的随机种群系统数值解的稳定性,讨论了带有Markovian转换的与年龄相关的随机种群系统的渐近稳定性[9];文献[10]针对与年龄相关的随机种群扩散系统,讨论了其数值解的指数稳定性.然而上述文献中,均是对随机种群模型数值解的稳定性进行了研究,但数值解的另一个性质渐近有界性同样具有重要的研究价值[11].本文利用EM方法研究具有年龄结构的随机种群系统的渐近有界性,在线性增长条件下,建立p阶矩渐近有界性准则.最后,通过数值算例对所得的结论进行了验证.

2 预备知识

令V=H1([0,A])其中是广义函数意义下的偏导数;V是Sobolev空间;H=L2([0,A]),满足是V的对偶空间;|·|和‖·‖分别为V,V′的范数;〈·,·〉表示V与V′空间的内积[10].

定义(Ω,F,{Ft}t≥0,P)是带流的单调递增完备的概率空间,F0包含所有的P零子集,B(t)是定义在概率空间(Ω,FtP)上的Brown运动.a∨b表示a和b的最大值,a∧b表示a和b的最小值.

定义2.1在概率空间(Ω,F,P)上的一个带流F的随机过程Pt被称为方程(1.1)的解,如果满足下列条件

(1)Pt∈I2(0,T;V)∩L2(Ω;(0,T;H)),其中I2(0,T;V)为所有均方可测的 (Pt)t∈[0,T]组成的空间,满足

(2)对于任意的t∈[0,T],在概率空间V′上下列方程几乎处处成立,

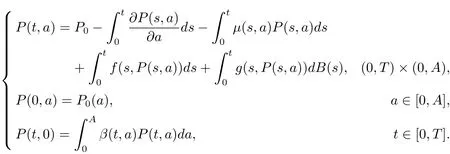
为了证明文中的结论,给出以下假设条件

(A1)方程(1.1)中f(t,P),g(t,P),满足线性增长条件,即

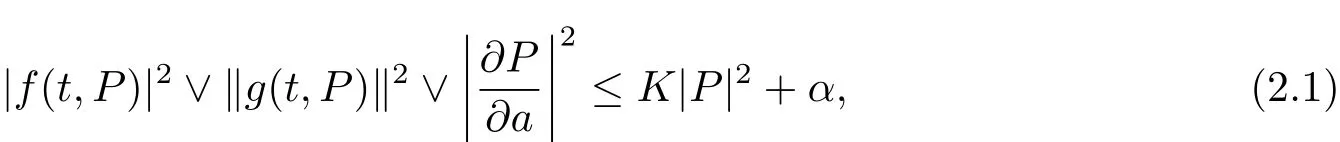
其中K和α均为正常数.

(A2)µ(t,a),β(t,a)在Q上是连续的且存在正常数µ0,¯µ,¯β,满足

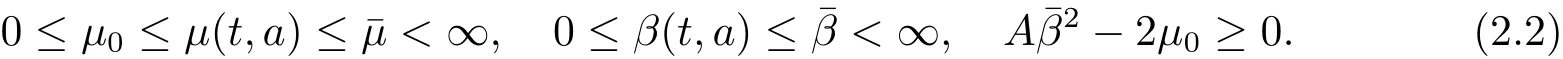
(A3)存在正常数D,使得对于任意P∈V,

其中λ是正常数,Qi(|P|)是|P|的i次多项式.

3 EM方法

本节将利用EM方法研究具有年龄结构的随机种群系统的渐近有界性,并建立p阶矩渐近有界性准则.

首先使用EM差分方法对方程(1.1)进行离散,可得

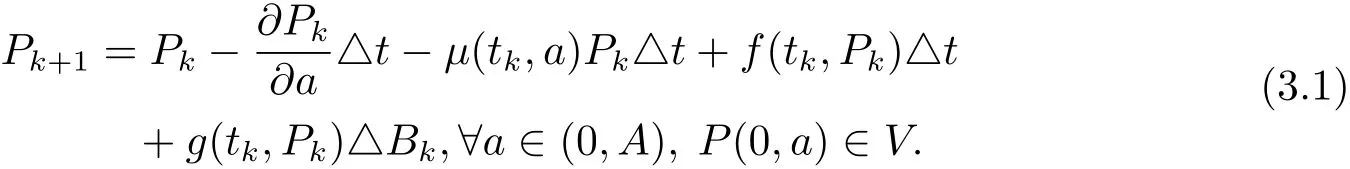
下面给出本文的主要定理.

定理3.1 如果条件(A1)–(A3)成立,那么对于任意的ε∈(0,λ),都存在常数p∗∈(0,1)和△t∗∈(0,1)使得∀p∈(0,p∗)和∀△t∈(0,△t∗),方程(3.1)的EM解满足

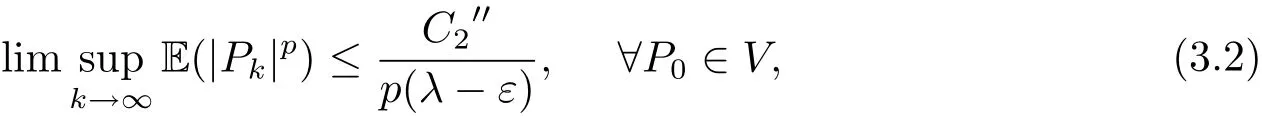
其中C2′′是与K、α、D和p有关,与P0无关的常正数.

证 由EM差分格式(3.1)可得

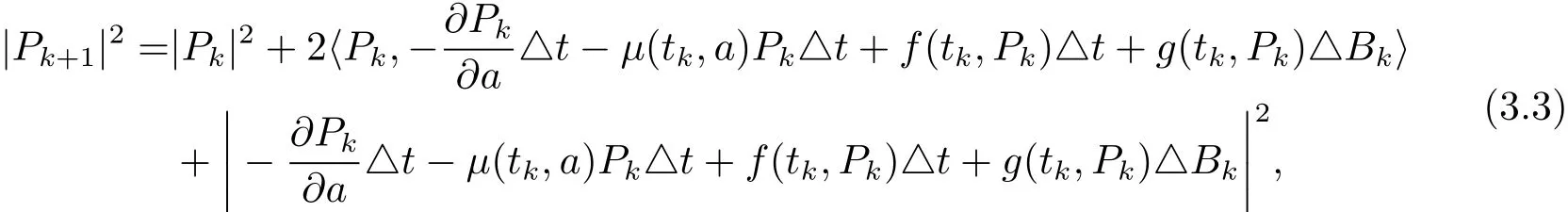
则对于常数D,有

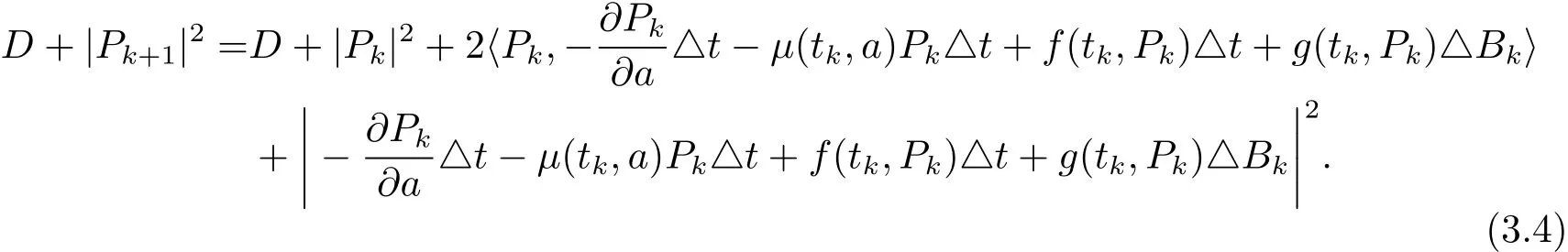
令

那么对于任意的p∈(0,1),满足

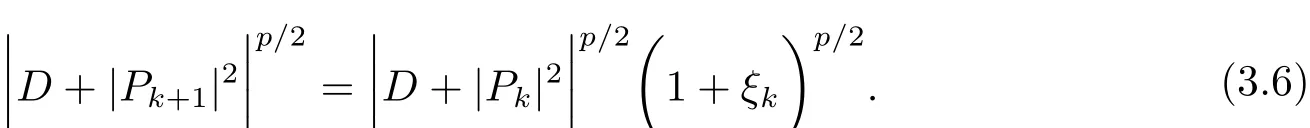
由基本不等式

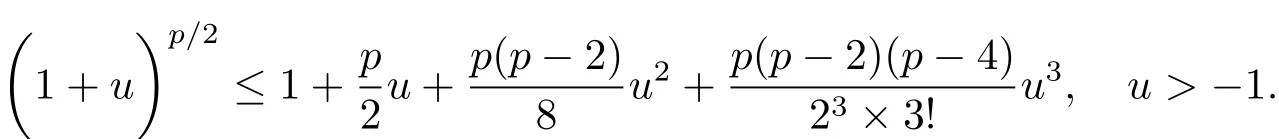
显然,ξk＞−1,由基本不等式可得

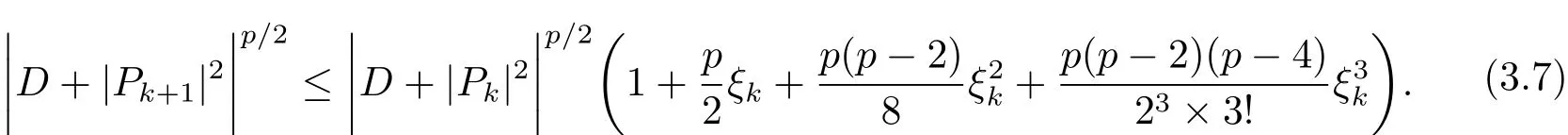
对(3.7)式两边同时取条件期望,有

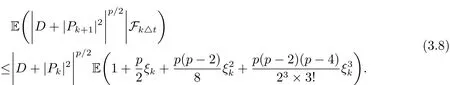
因为△Bk与Fk△t独立,所以 E(△Bk|Fk△t)=E(△Bk)=0,E((△Bk)2|Fk△t)=E((△Bk)2)=△t,因此

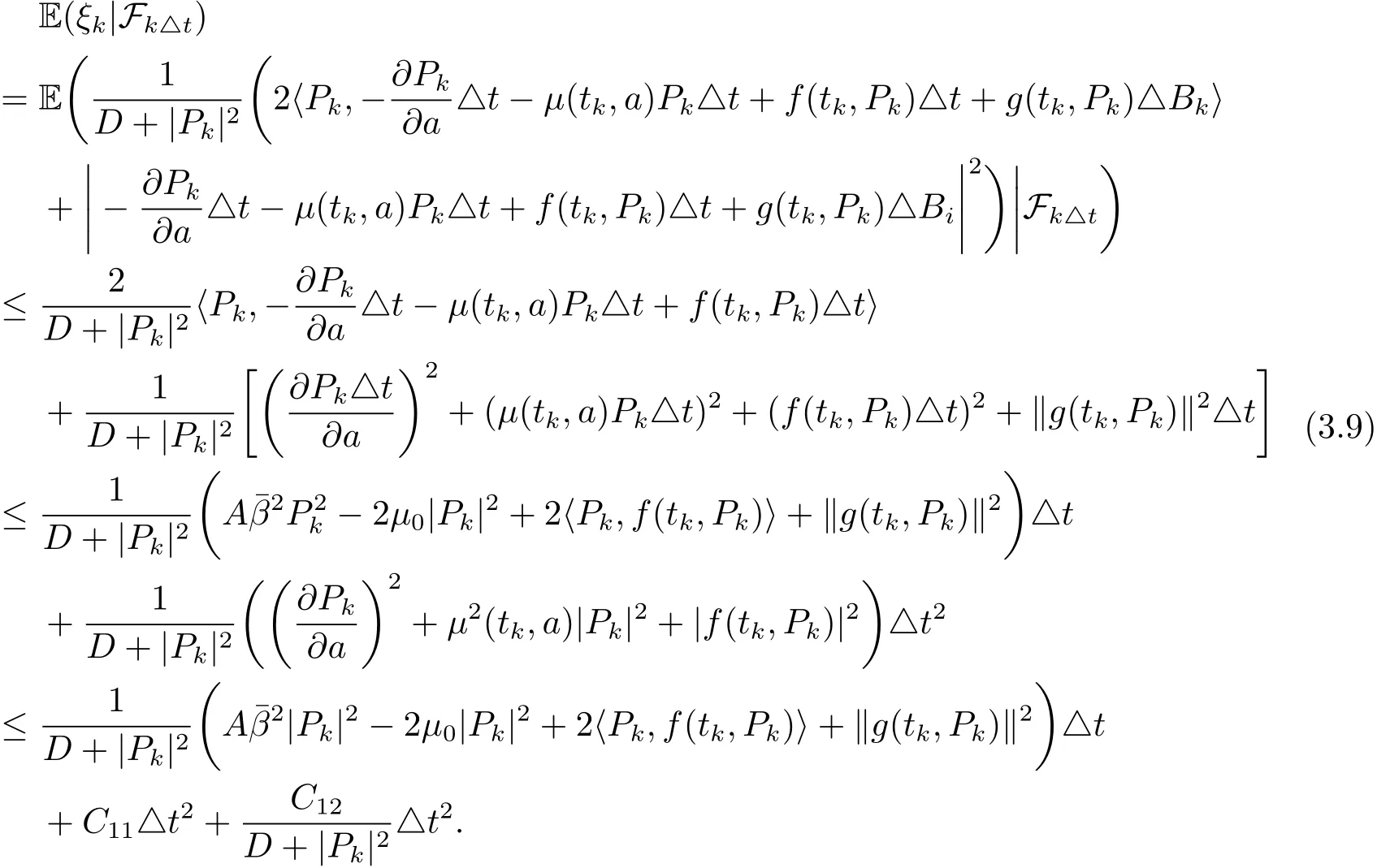
类似的,可得

其中C11,C21,C31,C12,C22,C32,均为正常数;C11,C21,C31与K有关;C12,C22,C32与α有关.现在考虑下面两个分数

当0＜p＜1时,两个分数的分子中|Pk|的次数分别为p+1次和p+3次,均小于对应分数分母中|Pk|的次数.所以对于任意的|Pk|∈R,两个分数都存在上界.同时,当i,j=1,2,3时,显然也有界.把(3.9)–(3.11)式代入(3.8)式,并且根据假设 (A1)–(A3)和 (3.12)式,可以得到

(1)药物治疗依从性:也就是遵医行为,采用评价高血压患者服药依从的4个问题来确定:当您服药自觉症状更坏时,是否曾停药?是否有时不注意服药?是否有忘记服药的经历?当您自觉症状改善时,是否曾停药?4个问题回答均为“否”即为依从性佳。(2)观察治疗前后两组收缩压与舒张压变化情况。

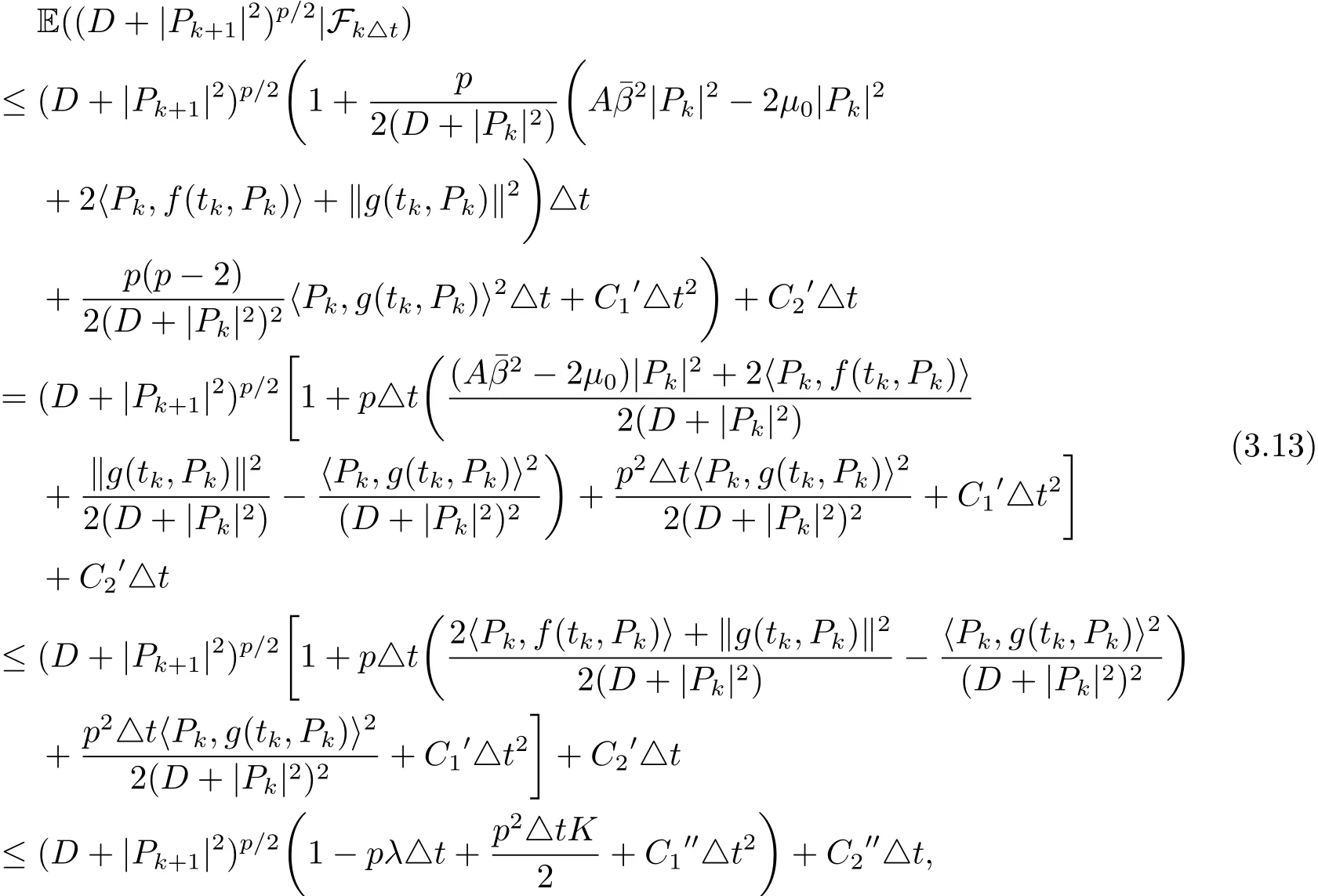
其中C1′,C1′′是与K和p有关的正常数,C2′,C2′′是与K,α,D和p有关的正常数.对于任意给定的ε∈(0,λ),取充分小的p∗∈(0,1)使得p∗K＜ε,同时取充分小的△t∗∈(0,1)使得则对于任意的p∈(0,p∗)和△t∈(0,△t∗),有

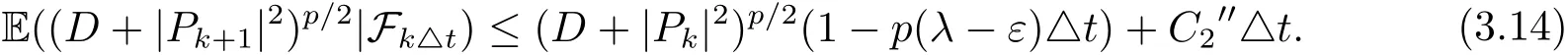
两边同时取期望,可得

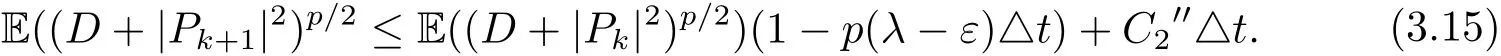
通过迭代,易知

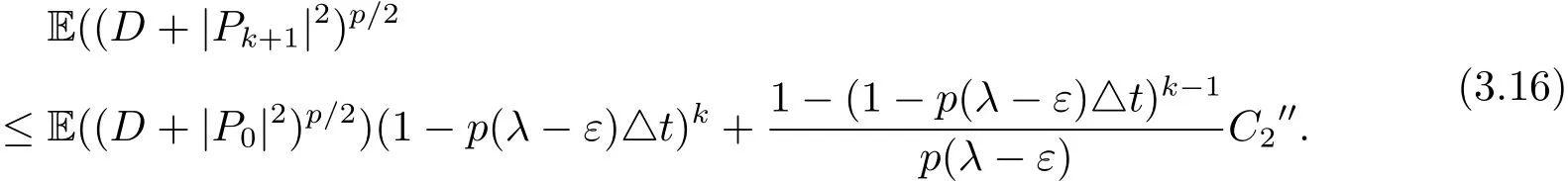
又因为E(|Pk|p)≤E((D+|Pk|2)p/2),所以

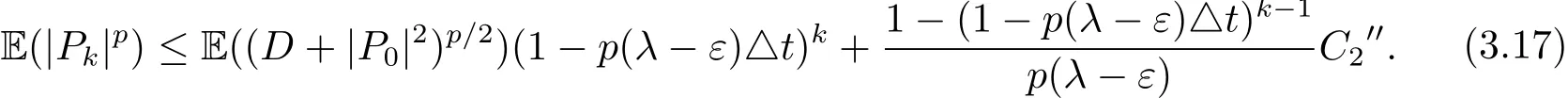
令k→∞,则

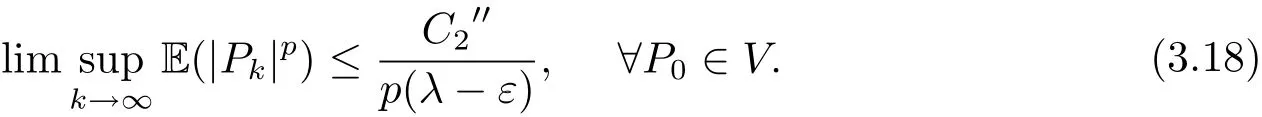
定理得证.

4 数值算例

本节通过以下例子对定理进行验证

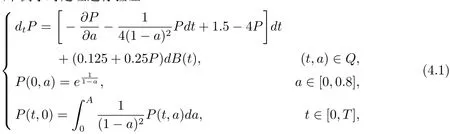
B(t)是标准布朗运动,g(t,P)=0.125+0.25P.显然f(t,P),g(t,P)均满足线性增长条件,同时,所以假设条件(A2)也成立.

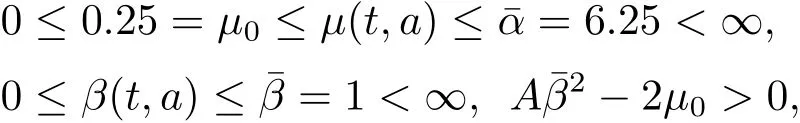
下面证明假设条件(A3)中D的存在性并给出D的选取过程.

记f(tk,Pk)=θ1+θ2Pk,g(tk,Pk)=σ1+σ2Pk,则对于假设条件(A3)有

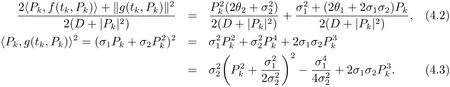
因此取

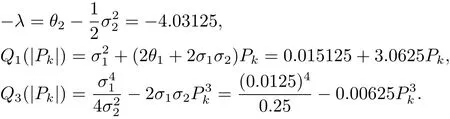
所以假设条件(A3)成立,即常数D存在并且

最后根据定理1的证明过程(3.4)–(3.18)式得到P(t,a)渐近有界.

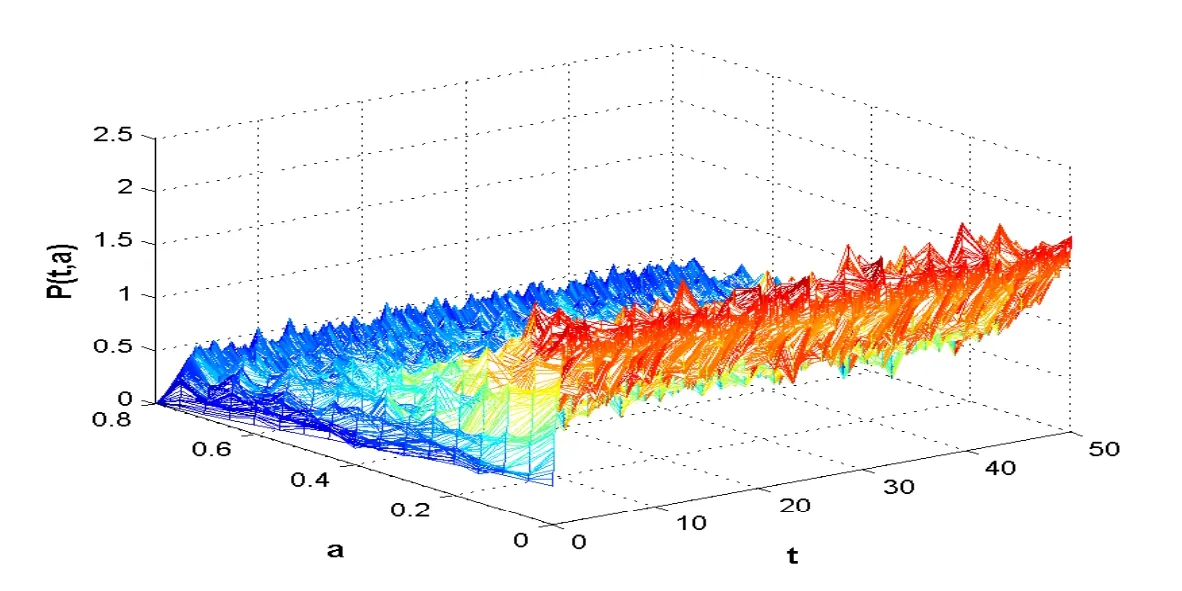
取时间步长Δt=0.01,空间步长h=0.05,采用EM方法对方程进行差分离散,分别作出该算例数值解的二维图(图1)和三维图(图2).由图可知当时间趋于无穷时,该种群系统的种群密度上下波动,并存在一个上界,显然,此种群系统渐近有界.

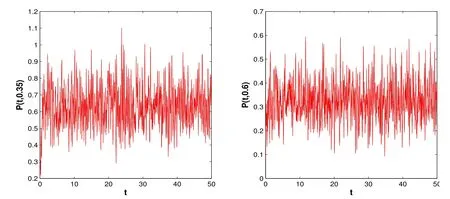
图2:P(t,a)数值解的二维轨迹

5 结论

本文基于EM方法研究了一类具有年龄结构的随机种群系统的数值解的p阶矩渐近有界性.在线性增长条件下,利用基本不等式建立了渐近有界性准则.所得结论为种群的最优控制提供了有效的工具.

[1]Jean J,Albert N,Shiriaev.Limit theorems for stochastic process[M].New York:Springer Verlag,2002.

[2]Luo Hui,Ma Xuemin,Ma Zhiwei,Zhou Xuan.The statistics analysis of randomly trimmed means and their bootstrap[J].J.Math.,2014,34(1):1–15.

[3]杨洪福,张启敏.与年龄相关的随机时分数阶种群系统温和解的存在性、唯一性[J].数学杂志,2016,36(5):1083–1090.

[4]李荣华,戴永红,孟红兵.与年龄相关的随机时滞种群方程的指数稳定性[J].数学年刊,2006,27A(1):39–52.

[5]Mao Xuerong.Stochastic differential equations and applcations[M].Chichester:Horwood Pulishing,2007.

[6]Mao Xuerong,Yuan Chenggui.Stochastic differential equations with Markovian switching[M].London:Imperial College Press,2006.

[7]Zhang Qimin,Liu Wenan,Nie Zankan.Existence,uniqueness and exponential stability for stochastic age-dependent population[J].Appl.Math.Comp.,2004,154:183–201.

[8]Mao Wei.Exponential stability of numerical solutions to stochastic age-dependent population equations with Poisson jumps[J].Engin.Tech.,2011,55:1103–1108.

[9]Ma Weijun,Zhang Qimin,Wang Zhanping.Asymptotic stability of stochastic age-dependent population equations with Markovian switching[J].Appl.Math.Comp.,2014,227:309–319.

[10]Zhang Qimin.Expontial stability of numerical solutions to a stochastic age-structured population system with diffusion[J].J.Comp.Appl.Math.,2008,220(1-2):22–33.

[11]Luo Qi,Mao Xuerong,Shen Yi.Generalised theory on asymptotic stability and boundedness of stochastic functional differential equations[J].Automatica,2011,47(9):2075–2081.