关于合数模上Hardy和的均值

王晓瑛,岳霞霞,刘华宁

(西北大学数学学院,陕西西安 710127)

1 引言

设整数h,q满足q＞0.经典的Dedekind和的定义为

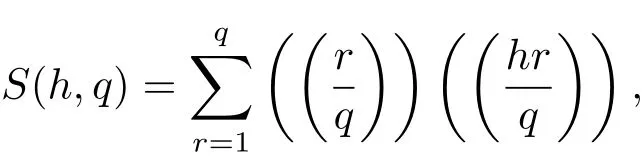
其中

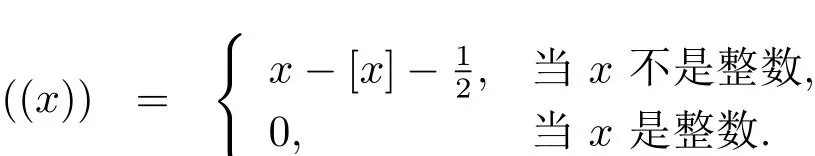
Dedekind和S(h,q)在Dedekindη函数的研究中起着重要作用,详见文献[1,2]或者[3]的第3部分.

Berndt[4]引入了如下的Hardy和

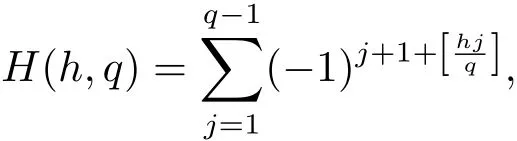
并研究了其性质.Sitaramachandrarao[5]将Hardy和表示成Dedekind和的如下形式

在文献[6]中,徐哲峰与张文鹏研究了短区间上的Hardy和的均值,并得到了如下渐近公式.

命题1.1设p≥5为素数,为b关于模p的乘法逆,则有

其中∈为任意小的正数.

Liu[7]也类似的研究了短区间上的Hardy和,并得到如下命题.

命题1.2设p≥5为素数,则有

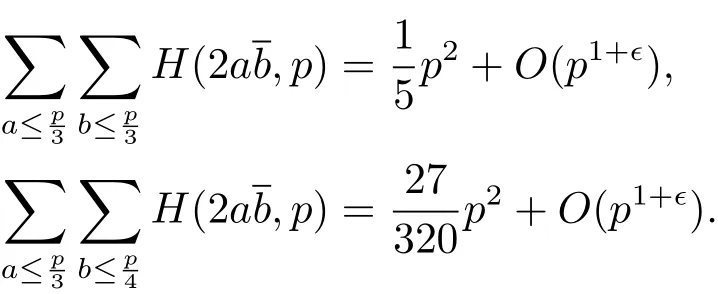
本文将进一步研究合数模上Hardy和的均值,主要结果如下.

定理1.1设q≥5为奇数,则有

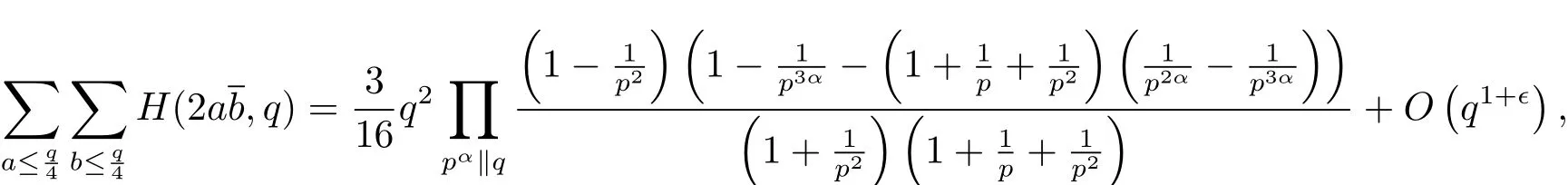
其中∈为任意小的正数.

首先将在第2节中把Hardy和的均值表为DirichletL-函数的均值;然后在第3节中计算相应的DirichletL-函数的均值;最后在第4节中证明定理1.1.

2 Hardy和的均值表为Dirichlet L-函数的均值

引理2.1设整数q,h满足q≥3与(h,q)=1,则有

证 见文献[8]中的引理2.

引理2.2设q≥3为奇数,h为任意整数,满足(h,q)=1.则有

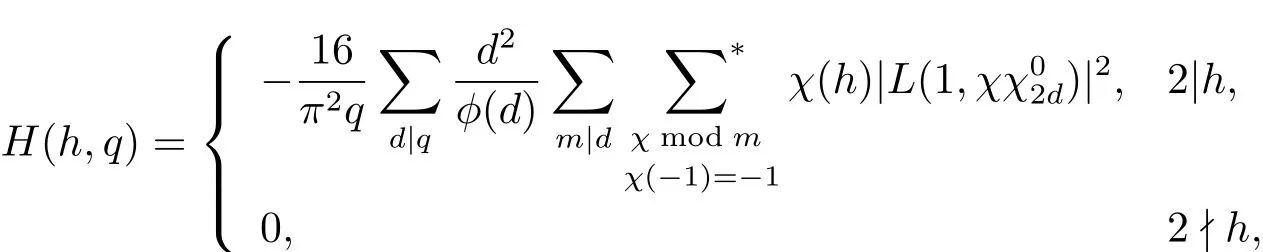
证 由引理2.1有

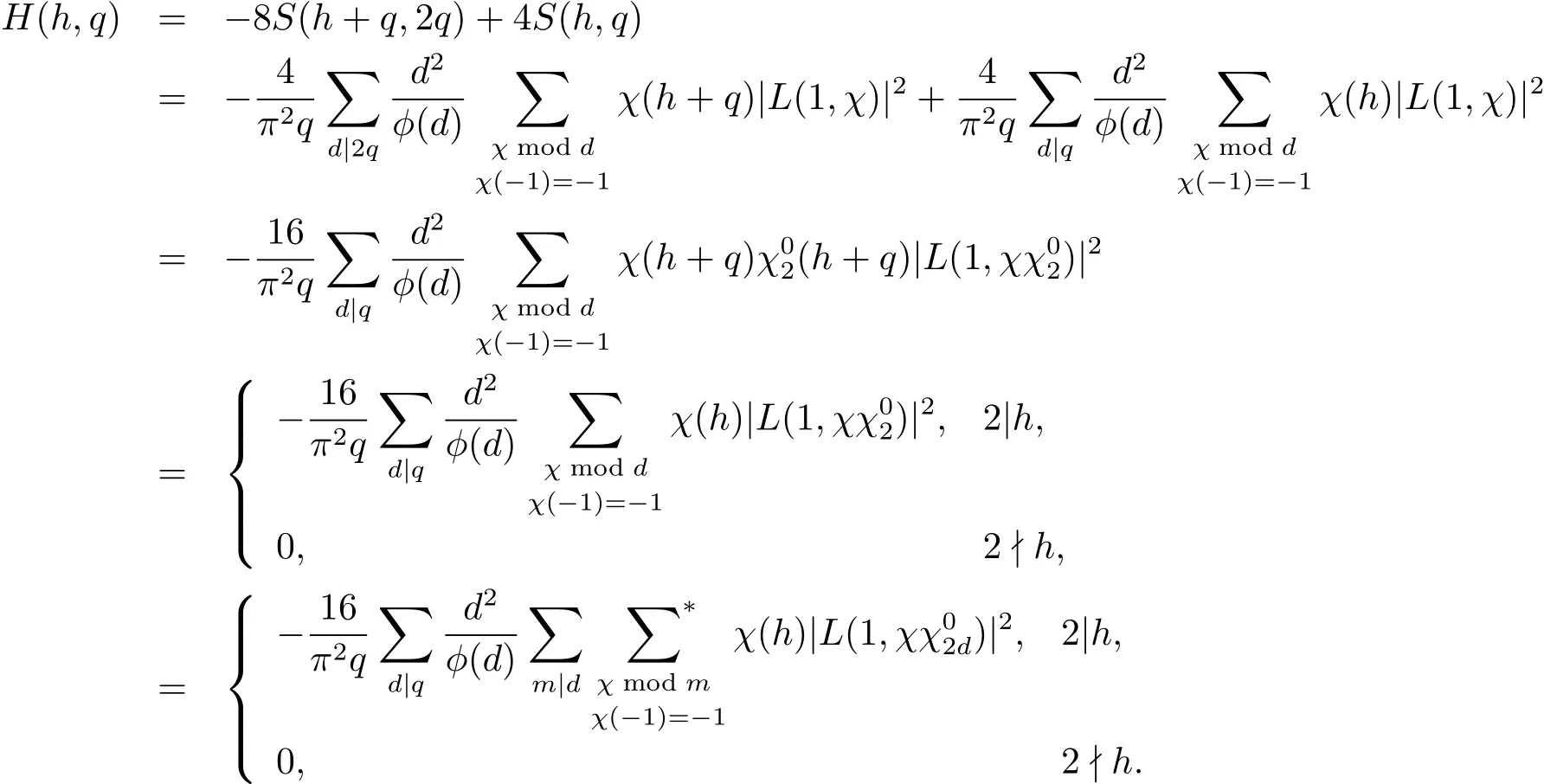
定理2.1 设q≥5为奇数,则有

证 由引理2.2可得

另一方面,设χ为模m的原特征,整数r≥1,λ∈[0,1)且由文献[9]可得特征和的Fourier展式如下

其中

是 Gauss和,e(y)=e2πiy.由此可得

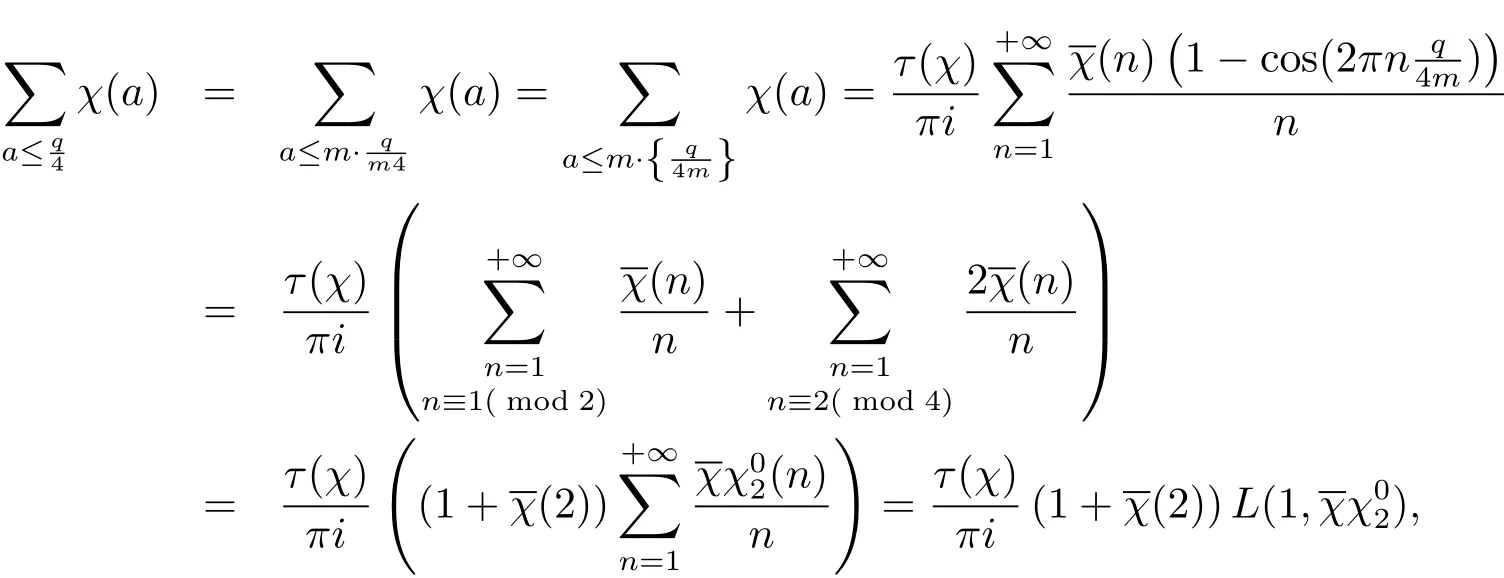
从而

3 Dirichlet L-函数的均值

引理3.1设整数m,r满足m≥2与(r,m)=1,χ为模m的Dirichlet特征.则有恒等式

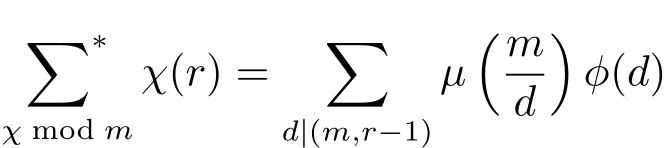
证 见文献[10]中的引理3.

引理3.2设d为奇数,则有

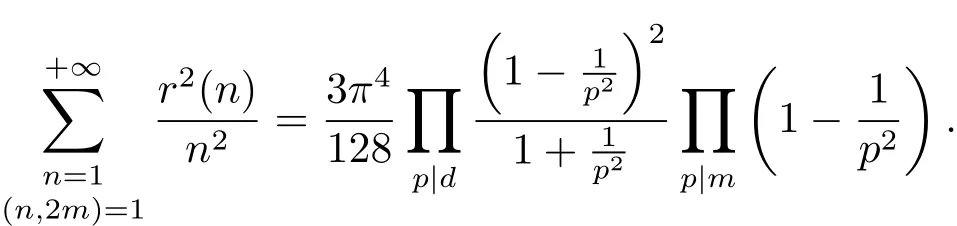
证 利用Euler乘积公式,有

其中ζ(s)是 Riemann Zeta函数,满足

定理3.1 设d为奇数,m|d,k为给定的正整数,则有

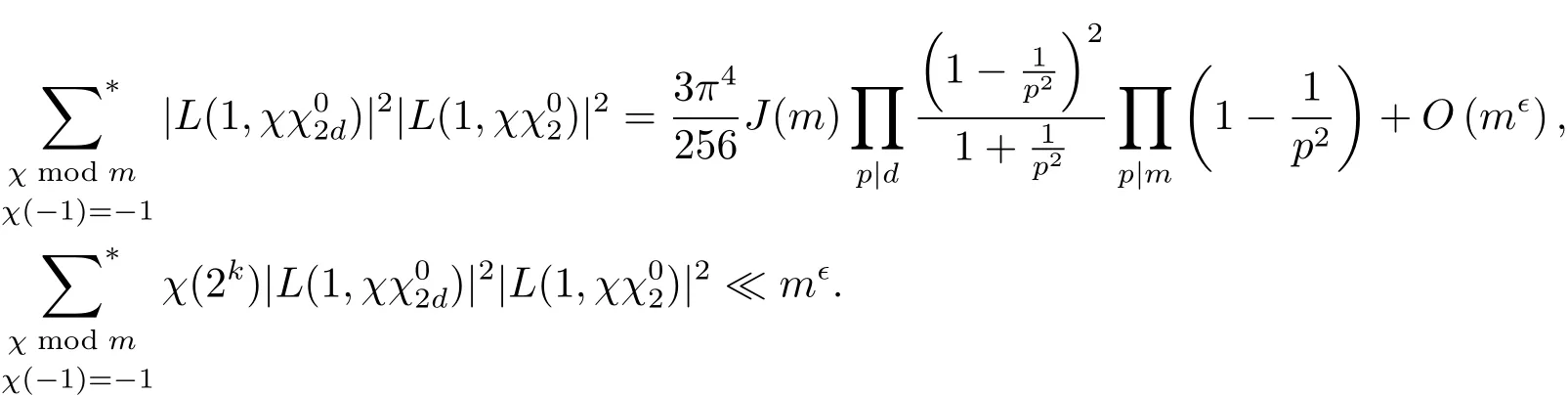
证 考虑非负整数k.令其中N为满足m≤N≤m4的参数,且由 Abel恒等式可得

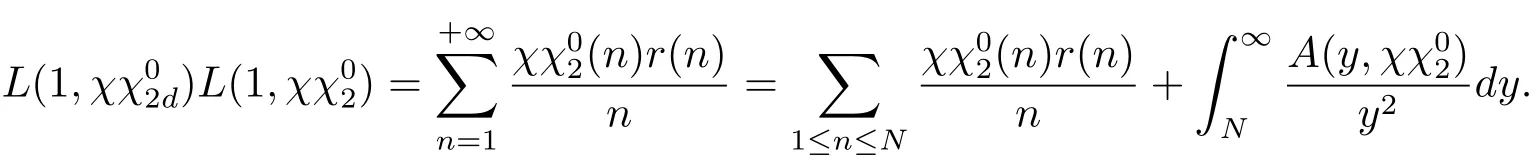
因此有

首先估计M2,M3与M4.注意到分拆恒等式

则有

因此

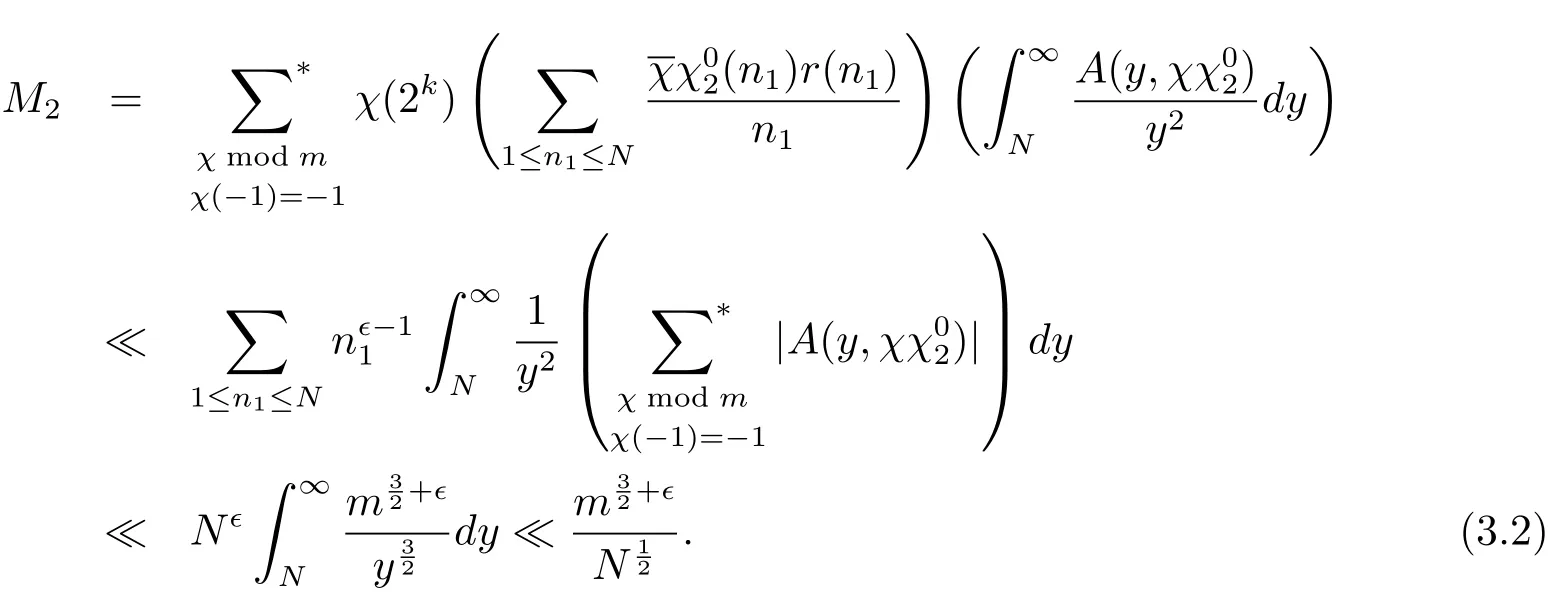
同理可得

此外利用Cauchy不等式,有

因此结合 (3.1)–(3.4)式可得

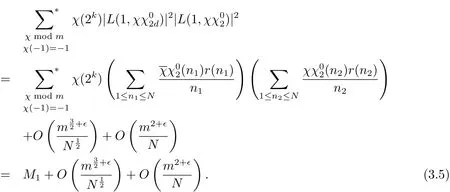
设(a,m)=1.由引理3.1有

从而

注意到估计式r(n)≪n∈.利用剩余系的性质可得

现在考虑M11.把对n1和n2的求和式分成下列四种情况讨论

不难证明

此外还有

以及

结合 (3.5)–(3.10)式可得

当k≥1时,取N=m3,有

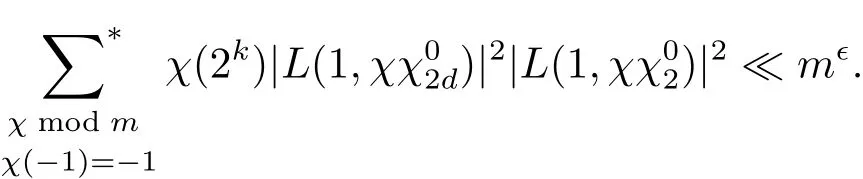
而当k=0时,取N=m3,并利用引理3.2可得

4 定理1.1的证明

由定理2.1与定理3.1有

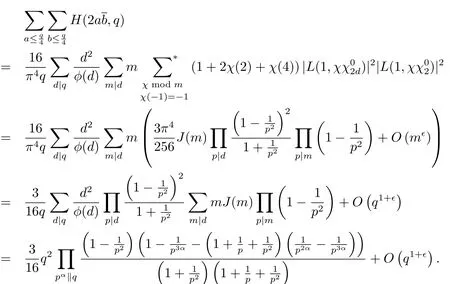
这就证明了定理1.1.

[1]陈国慧,刘宝利.关于Dedekind和的一些恒等式[J].数学杂志,2014,34(2):198–204.

[2]Rademacher H.Dedekind sums[M].Washington:Math.Assoc.Amer.,1972.

[3]Apostol T M.Modular function and Dirichlet series in number theory[M].New York:Springer-Verlag,1976.

[4]Berndt B C.Analytic Eisenstein series,theta-functions,and series relations in the spirit of Ramanujan[J].J.Reine Angew.Math.,1978,303/304:332–365.

[5]Sitaramachandrarao R.Dedekind and Hardy sums[J].Acta Arith.,1987,48(4):325–340.

[6]Xu Z,Zhang W.The mean value of Hardy sums over short intervals[J].Proc.Roy.Soc.Edinburgh Sect.A,2007,137(4):885–894.

[7]Liu W.Mean value of Hardy sums over short intervals[J].Acta Math.Acad.Paedagog.Nyh´azi.(N.S.),2012,28(1):1–11.

[8]Zhang W.On the mean values of Dedekind Sums[J].J.Th´eor.Nombres Bordeaux,1996,8(2):429–442.

[9]P´olya G.¨Uber die verteilung der quadratischen reste and nicht-reste[J].G¨ottingen Nachrichten,1918:21–29.

[10]Zhang W.On a Cochrane sum and its hybrid mean value formula[J].J.Math.Anal.Appl.,2002,267(1):89–96.