具有Prey-Taxis的Holling-Tanner捕食模型的分支结构

张晓杰,张丽娜

(西北师范大学数学与统计学院,甘肃兰州 730070)

1 引言

本文讨论如下具有prey-taxis的Holling-Tanner捕食模型

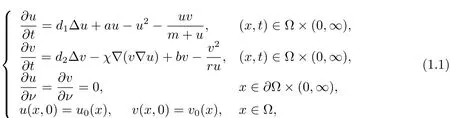
其中u,v分别表示食饵和捕食者的密度函数,a,b是其各自的内禀增长率,ru可解释为依赖于食饵的捕食者的承载能力,u/(m+u)是Holling II型功能反应函数,表示捕食者吃食饵的速率.参数a,m,b,r均为正常数.正常数d1,d2为扩散系数,χ∇(v∇u)为prey-taxis项.齐次Neumann边界条件意味着该生态系统是自我封闭的,在边界∂Ω上物种的流量为零.

模型(1.1)所对应的常微分方程系统(即(1.1)式中d1=d2=χ=0)被称为Holling-Tanner捕食模型[1],是数学家和生物学家Robert May为了能够精确地描述诸如山猫和野兔、麻雀和食雀鹰等生态系统物种间的相互作用而提出的一个新的具有Holling响应函数的模型[2],由于其重要的生物意义和特有的数学特性,该模型得到了大量的研究,如稳定的极限环、半稳定的极限环、分支、周期解等有趣的数学现象均被发现[3–5].考虑到种群密度空间分布不均匀因素,彭锐等在文献[6,7]中关注了具有扩散的Holling-Tanner捕食模型(即(1.1)式中χ=0),获得了非常数正解的存在性和不存在性的一些结果,给出了唯一的正常数平衡解全局渐近稳定的一些充分条件.

事实上,在现实生态环境中,物种的扩散往往还会受到其他物种的影响.这些物种间的相互作用可以通过交错扩散模型来描述,相应的数学模型是强耦合的非线性偏微分方程组[8,9].与仅带一般扩散的弱耦合系统相比,强耦合的系统在理论研究和数值计算两方面都存在更大的困难.模型(1.1)中prey-taxis项χ∇(v∇u)就是一种交错扩散项,如果χ＞0称趋化吸引,表示捕食者向食饵密度增大的方向运动,即捕食者追逐食饵.如果χ＜0称趋化排斥,表示捕食者向食饵密度减小的方向运动,从生物学的角度来看,这表示食饵聚集起来形成了一个团结互助、共同抵御外敌的群体,从而保护自己免受捕食者的攻击[10].

本文主要关注prey-taxis项对平衡态斑图的影响.我们的结果表明趋化吸引具有稳定化作用,会抑制平衡态斑图生成,而趋化排斥具有不稳定化作用,会导致平衡态斑图生成.具体地,我们首先对模型(1.1)的线性稳定性进行详细的分析,得到唯一正常数平衡点(u∗,v∗)的一些稳定性结果.然后应用Crandall-Rabinowitz分支理论[11],以趋化系数χ为分支参数,讨论模型(1.1)的正分支解的存在性以及分支方向,从而对平衡态斑图的结构进行更深刻的刻画.

2 稳定性分析

易知,系统(1.1)存在唯一的正常数平衡解(u∗,v∗),其中

为简便起见,记

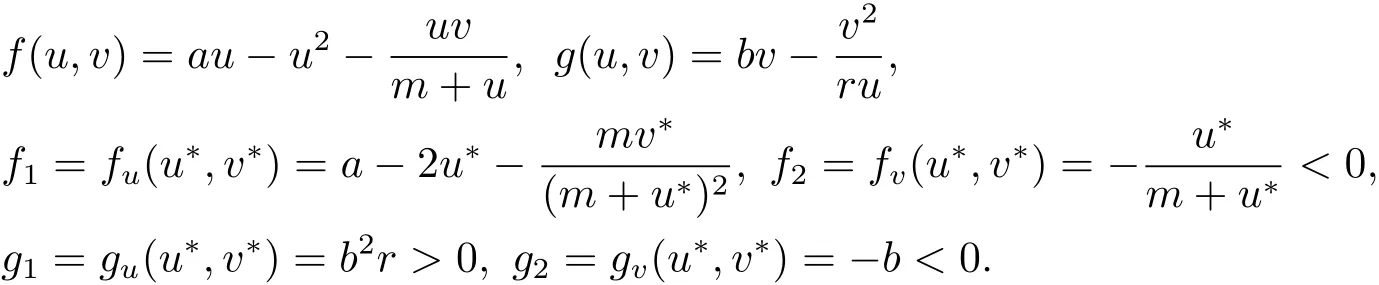
在全文中,总假设

成立.这意味着(u∗,v∗)作为系统(1.1)相应的常微分系统的常数平衡点是稳定的.

令0=µ0＜µ1≤µ2≤µ3≤···是椭圆算子−Δ在¯Ω上相应于齐次Neumann边界条件的特征值,每个特征值µi的重数为mi≥1,φij,1≤j≤mi为µi标准化的特征函数,则集合{φij|i≥0,1≤j≤mi}构成L2(Ω)空间中的一组完备正交基,记Xij={cφij:c∈R2},下面用线性化分析的方法得到系统(1.1)唯一的正常数平衡点(u∗,v∗)的线性稳定性结果.

考察线性化算子

对于每一个i≥0,Xi在算子L0的作用下是不变的,η是L0在Xi上的特征值当且仅当η是矩阵的特征值.特征方程为η2−Pi(µi,χ)η+Qi(µi,χ)=0,其中

显然,Pi(µi,χ)=Pi(µi,0),Qi(µi,χ)=Qi(µi,0)−χv∗f2µi. 记

注意到f2＜0和假设条件(H0),易于得到下述定理.

定理2.1 (i)如果Pi(µi,0)＜0,Qi(µi,0)＞0对所有的i≥1成立.则对所有的χ＞0,系统(1.1)唯一的正常数平衡点(u∗,v∗)是局部渐近稳定的.

(ii)如果对所有的i≥0,Pi(µi,0)＜0,存在某些i≥1使得Qi(µi,0)＜0成立.记Λ1={i|i≥1,Qi(µi,0)＜0}.则对所有的系统(1.1)唯一的正常数平衡点(u∗,v∗)是局部渐近稳定的.

(iii)如果Pi(µi,0)＜0,Qi(µi,0)＞0对所有的i≥1成立.则对所有的系统(1.1)唯一的正常数平衡点(u∗,v∗)是不稳定的.

定理2.1(i)表明,无趋化时(χ=0)稳定的正常数平衡点在捕食者对食饵的趋化是吸引(χ＞0)时仍保持稳定.定理2.1(ii)意味着常微分系统稳定的常数平衡点,在只有扩散而无趋化时由于扩散导致的不稳定,当捕食者对食饵的趋化吸引出现时,会将这种扩散导致的不稳定再次变得稳定.也就是说,趋化吸引具有稳定化作用,会抑制斑图的生成.定理2.1(iii)表明,对于常微分系统和只有扩散的偏微分系统均稳定的常数平衡点,捕食者对食饵的趋化排斥会导致常数平衡点不稳定.即趋化排斥具有不稳定化作用,可能会导致斑图生成.

3 局部分支

显然当f1＜0时,(2.2)和(2.3)式中Pi(µi,0)＜0,Qi(µi,0)＞0对所有的i≥1成立.定理2.1的(i)和(iii)意味着只有趋化排斥才可能导致斑图生成.本节在条件f1＜0下,以趋化系数χ＜0为分支参数,应用分支理论证明非常数正平衡解的存在性,从而说明趋化排斥确实会导致平衡态斑图生成.

为了简便起见,在一维空间Ω=(0,l),l＞0上讨论.对于高维情形可类似讨论.即关注平衡态系统

在一维情况下,µi=(πi/l)2,相应的标准化的特征函数为

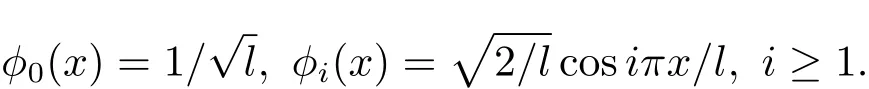
令Y=L2(0,l)×L2(0,l)是一个Hilbert空间,其内积形式为(U1,U2)Y=(u1,u2)L2(0,l)+(v1,v2)L2(0,l),¯X={(u,v):u,v∈L2(0,l),u′=v′=0,x=0,x=l}.定义算子F:RׯX→Y,

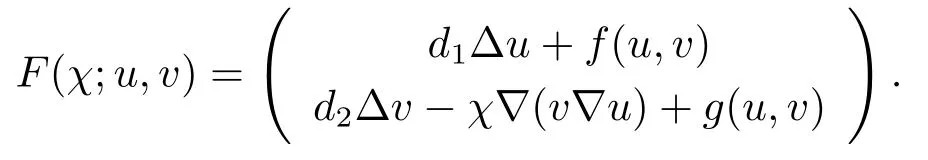
首先,在平凡解曲线Γ={χ;(u∗,v∗)}⊆R×X上寻找所有可能的分支点.

根据隐函数定理,若(χ;u∗,v∗)是一个分支点,则算子F(χ;u,v)关于(u,v)的导算子F(u,v)(χ;u,v)在(χ;u∗,v∗)处退化.由第2部分稳定性分析的过程知,在(2.1)式线性化算子L0中取χ=χi,则L0(χi)=F(u,v)(χi;u∗,v∗). 易见 (2.3)式中χ=χi时Qi(µi,χi)=0,算子F(u,v)(χi;u∗,v∗)具有零特征值.这意味着对所有的i≥1,(χi;u∗,v∗)均为可能的分支点.

定理3.1假设f1＜0成立.设i是一个正整数,若i/=j时,χi/=χj,则存在一个正常数δ使得系统(3.1)在分支点(χi;u∗,v∗)邻域中的非常数正解可以表示为

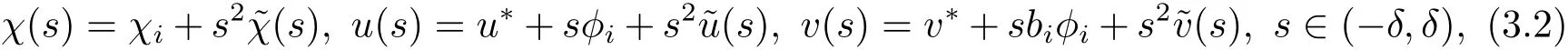
证 由定理的假设条件知

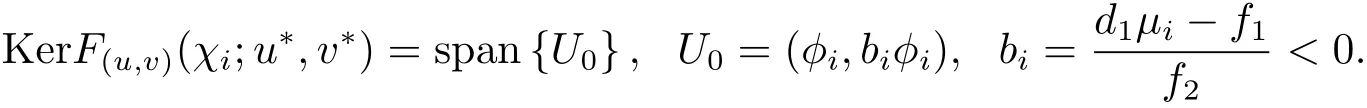
考虑F(u,v)(χi;u∗,v∗)的共轭算子易于验证

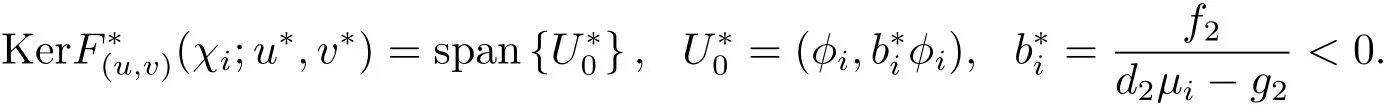
由Fr´edholm 二择一定理,

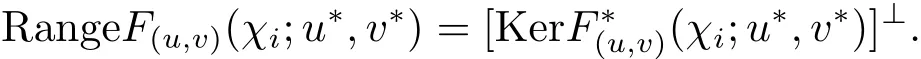
因此 codim RangeF(u,v)(χi;u∗,v∗)=1.由于

故Fχ,(u,v)(χi;u∗,v∗)U0/∈RangeF(u,v)(χi;u∗,v∗).由局部分支定理[11],系统(3.1)存在一条由点(χi;u∗,v∗)分支出的非平凡解曲线(χ(s);u(s),v(s)),其中u(s)=u∗+sφi+s2˜u(s),v(s)=v∗+sbiφi+s2˜v(s),χ(s)=χi+sβ(s),s∈(−δ,δ),˜χ(s),˜u(s),˜v(s)是关于s的光滑函数,且满足

为了证明(3.2)式,只需要证明β(0)=0.为方便起见,记f11=fuu(u∗,v∗),f12=fuv(u∗,v∗),g11=guu(u∗,v∗),g12=guv(u∗,v∗). 将 (χ(s);u(s),v(s)) 代入 (3.1) 式的第一个方程,关于s求导两次后令s=0得

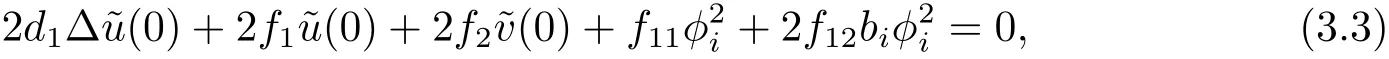
(3.3)式与φi作L2-内积,运用Green’s公式并注意

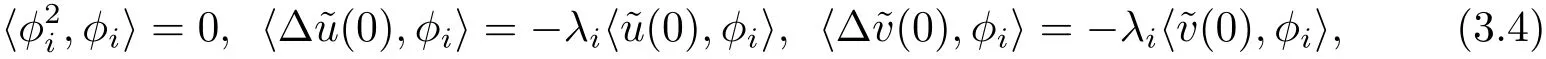
可得

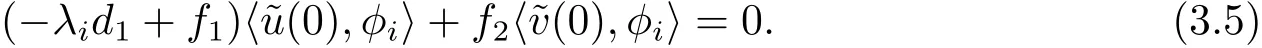
另一方面,将(χ(s);u(s),v(s))代入(3.1)式的第二个方程,关于s求导两次后令s=0得

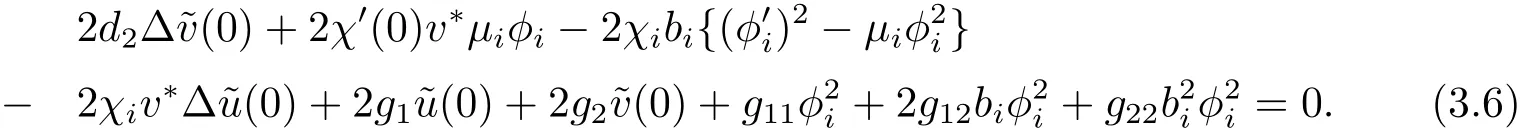
将(3.6)式与φi作L2-内积,结合(3.4)式,并注意到可得

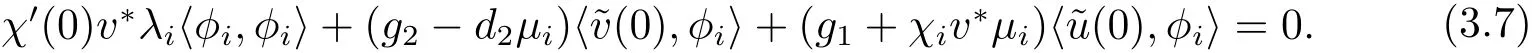
由χi的定义式 (2.4),得g1+χiv∗则(3.7)式等价于

将(3.5)式代入(3.8)式,得β(0)=χ′(0)=0.定理得证.

4 分支方向

在这一小节,讨论定理3.1中所得到的局部分支解的分支方向.本小节的目的是求出具体的表达式,它决定了分支曲线(3.2)在点(χi;u∗,v∗)处相应于平凡解曲线Γ的分支方向.如果则通常称分支为超临界的;如果则称分支为次临界的.下面的定理告诉我们可由四个L2-内积

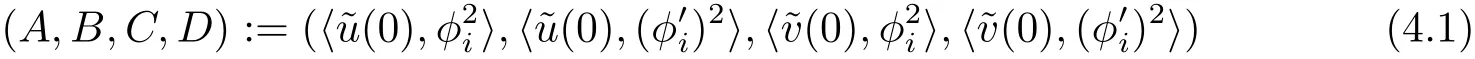
来表示.

定理4.1(3.2)式中的函数˜χ(s)满足

其中f111:=fuuu(u∗,v∗),f112:=fuuv(u∗,v∗),g111:=guuu(u∗,v∗),g112:=guuv(u∗,v∗),g122:=guvv(u∗,v∗).

关于(A,B,C,D),有如下引理.

引理4.2(A,B,C,D)满足下述代数方程组

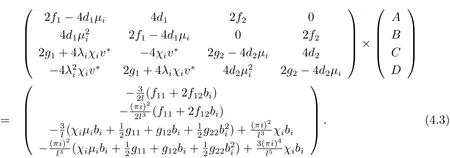
易得到(4.3)式.证明从略.

定理4.1的证明将(χ(s);u(s),v(s))分别代入(3.1)式的两个方程,关于s求导三次后令s=0得作L2-内积,通过分部积分并注意到

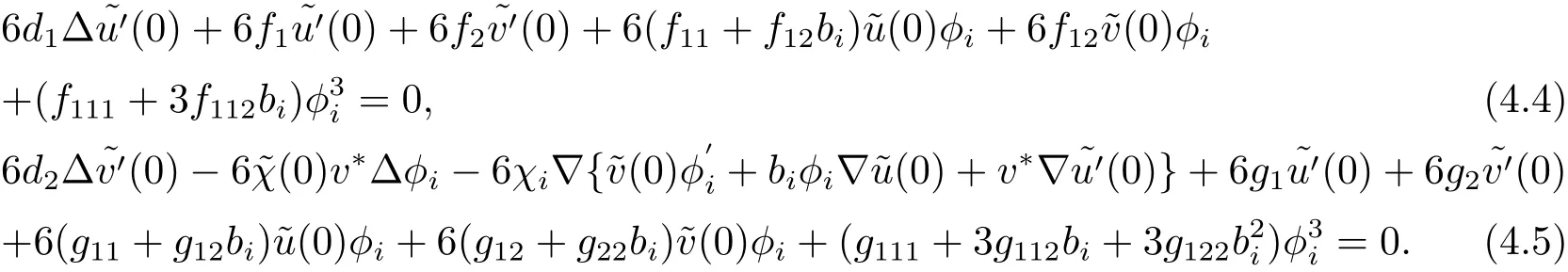
将(4.4),(4.5)式分别与φi作L2-内积,由分部积分得

再次注意到〈φi,φi〉=1,并且在(4.6)和(4.7)式中和的系数间对应成比例,将(4.7)式代入(4.6)式即得(4.2)式.定理4.1证毕.

[1]S´aez E,Gonz´alez-Olivares E.Dynamies of a predator-prey model[J].SIAM J.Appl.Math.,1999,59(3):1867–1878.

[2]Holling C S.The functional response of invertebrate predators to prey density[J].Mem.Ent.Soc.Can.,1965,45(4):3–60.

[3]Braza P A.The bifurcation structure of the Holling-Tanner model for predator-prey interations using two-timings[J].SIAM J.Appl.Math.,2003,63(2):889–904.

[4]Collings J B.Bifurcation and stability analysis of a tempreture-dependent of predator-prey interation model incorporating a prey-refuge[J].Bull.Math.Biol.,1995,57(3):63–76.

[5]May R M.Limit cycles in predator-prey communities[J].Sci.,1972,77(2)：900–902.

[6]Peng Rui,Wang Mingxin.Positive steady-states of the Holling-Tanner prey-predator model with diffusion[J].Proc.Roy.Soc.Edinburgh.Sect A.,2005,135(4):149–164.

[7]Peng Rui,Wang Mingxin.Global stability of the equilibrium of a diffusive Holling-Tanner preypredator model[J].Appl.Math.Lett.,2007,20(3):664–670.

[8]张艳红.三种群的竞争系统全局解的一致有界性[J].数学杂志,2012,32(6):1129–1135.

[9]Chen Xueyong,Zhang Jincai.The behavior of the solutions to a multi-group chemotaxis model with reproduction term[J].J.Math.,2011,31(5):853–860.

[10]Wang Xiaoli,Wang Wendi,Zhang Guohong.Global bifurcation of solutions for a predator-prey model with prey-taxis[J].Math.Meth.Appl.Sci.,2015,38(2):431–443.

[11]Crandall M G,Rabinowitz P H.Bifurcation from simple eigenvalues[J].J.Funct.Anal.,1971,8(4):321–340.