STABILITY OF COMPLETENESS FOR EXPONENTIAL SYSTEMS IN THE WEIGHTED BANACH SPACES

YANG Xiang-dong,WANG Yue

(Department of Mathematics,Kunming University of Science and Technology,Kunming 650093,China)

1 Introduction

Letα(t)be a nonnegative continuous function defined on R such that

The weighted Banach spaceCαconsists of complex continuous functionsfdefined on the real axis R withf(t)exp(−α(t))vanishing at infinity,equipped with the norm

Let M(Λ)denote the set of functions which are finite linear combinations of exponential system{eλt:λ∈Λ}with exponents Λ ={λn:n=1,2,···}which is a sequence of complex numbers.Condition(1.1)guarantees that M(Λ)is a subspace ofCα.

The completeness of M(Λ)inCαwas studied in many settings.Much was written about the properties of completeness and the closure of M(Λ)(see[1–6]and[11–15],for example).There was an interest in the study of stability of the completeness for the exponential systems in the weighted Banach spaces.We are aware of many results in this direction are on the stability of the completeness for exponential systems in the spacesC[−a,a]andLp(−a,a)(see[7,12,13]).Motivated by the work of B.N.Khabibullin(see[7–10]),our purpose here is to study the stability of the completeness for exponential systems inCα.Our approach to the problem is different from theirs.Combination of Deng’s work on the completeness ofexponential systems inCα(see[1])and Khabibullin’s work on subharmonic interpretation of shifts of zeros of entire functions allows us to characterize the stability of the completeness of M(Λ)inCα.

We now give a brief description of the results obtained.In Section 2,we show that under certain nearness conditions on Λ ={λn}and Γ ={γn}which are complex sequences with gaps in the right half plane,M(Λ)and M(Γ)are complete or incomplete inCαsimultaneously.In Section 3,we characterize the stability of M(Λ)inCαwherever Λ ={λn,µn}is a positive sequence,wherever eachλnappearingµntimes withµnnot necessarily bounded.

Notations For a complex sequence Γ ={γn},the finite linear combination of{eγt:γ∈Γ}is denoted by M(Γ).The symbolD(a,t)is used to denote the disk|z−a|＜t.The letterAdenotes positive constants and it may be different at each occurrence.Throughout this paper,the right half-plane{z=x+iy:x＞0}is denoted by C+.

2 The Exponents with No Multiplicity

In this section,we will consider the stability problem wherever the gap exponents with no multiplicity.More precisely,the exponents is defined as follows.Let Λ ={λn=|λn|eiθn:n=1,2,···}be a sequence of complex numbers satisfying

and

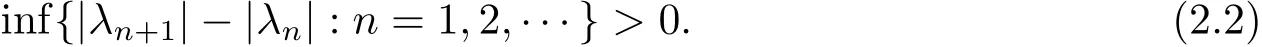
The main result of this section is described as follows.

Theorem 2.1 Letα(t)be a nonnegative convex on R satisfying(1.1).If two sequences of complex numbers Λ ={λn}and Γ ={γn}satisfy(2.1)and(2.2),furthermore,there exist a decreasing functionβ:[0,+∞)→(0,+∞)and a positive sequence{tn}that is linked with the sequence such that

then M(Λ)and M(Γ)are complete or incomplete inCαsimultaneously.

We will make use of the following result from[1].

Lemma 2.1(see[1])If Λ ={λn=|λn|eiθn:n=1,2,···}is a complex sequence satisfying(2.1)and(2.2),then the function

is analytic in the right half-plane C+,and vanishes exactly on the sequence Λ ={λn=|λn|eiθn:n=1,2,···}.Withr=|z|andx=ℜz,for some positive constantA,

whereλ(r)=2otherwise.

The crux of the proof of the following proposition is the method applied to shifts of zeros of entire functions.By this approach,we show that for a function analytic in the right half-plane C+,shifts of its zeros generate another function analytic in the right half-plane whose growth and zeros are very similar to the original one.

Proposition 2.1 LetG(z)be a function analytic in the right half-plane C+which is defined in(2.4)and vanishes exactly on the sequence Λ ={λn=|λn|eiθn:n=1,2,···},where Λ satisfies(2.1)and(2.2).Given a decreasing functionβ:[0,+∞)→(0,+∞),we can find a functionG1(z)analytic in the right half-plane C+={z=x+iy:x＞0}with sequence of simple zeros Γ ={γn=|γn|eiϑn:n=1,2,···}satisfies(2.1)and(2.2),furthermore,we can find a positive sequence{tn}that is linked with the sequences such that(2.3)is satisfied and for allz∈

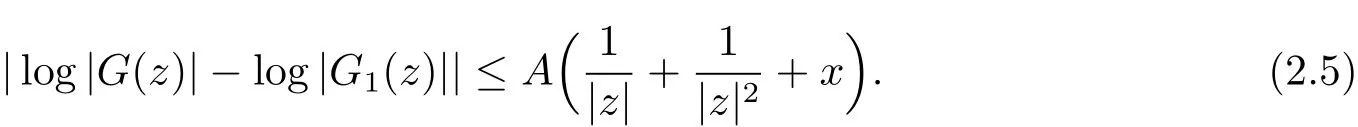
Proof Since the zeros ofG(z)have a gap,we can choose a sequence of strict positive numbers{tn}such that the disksD(λn,tn)are mutually disjoint and(2.3)is satisfied.We can also select strict positive numberdnsuch that

We will estimate the sum of differences

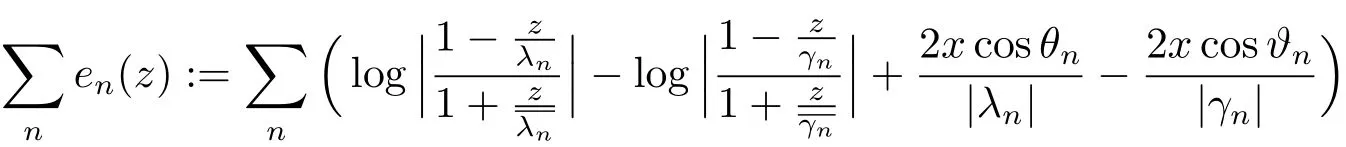
for allz∈C+Firstly,we establish an upper bound foren(z):

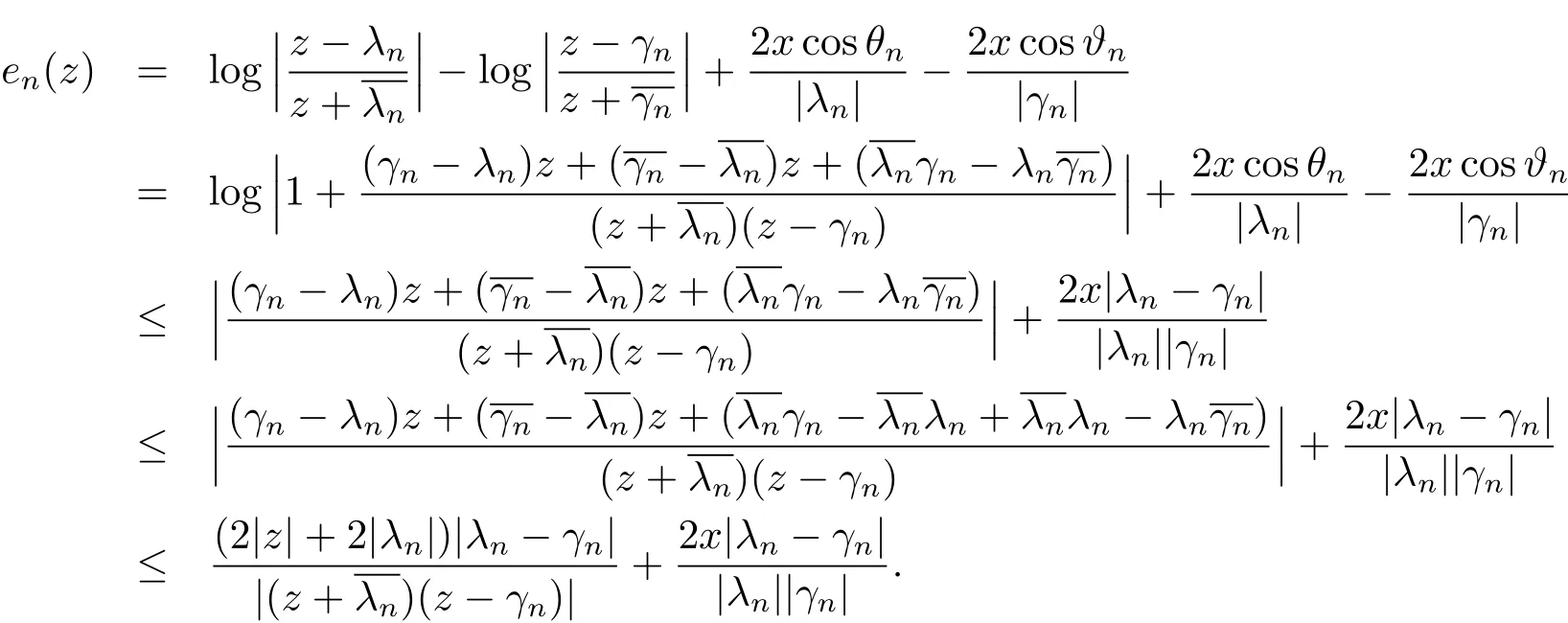
Forz∈C+andℜλn＞0,we have|z−λn|≤|zIf we choose a positive sequencednwhich satisfies(2.6),then|z−γn|≥|z−λn|−|γn−λn|≥thus

Second,we establish an upper bound for−en(z):

Forz∈C+andℜλn＞0,we have|z− γn|≤|z+γn|.If we choose a positive sequencednwhich satisfies(2.6),then|z−γn|and we have

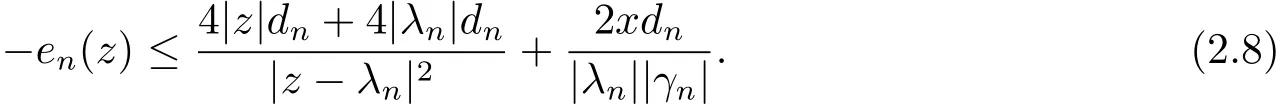
Combine(2.7)with(2.8),for allz∈we have

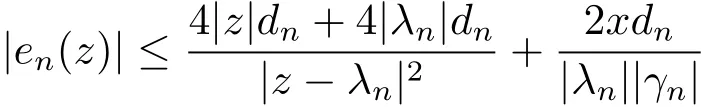
and

By(2.2),(2.3)and(2.6),we have

Fix a pointz∈D(λn,tn),

Hence,we can estimate the first sum as

and the second sum as

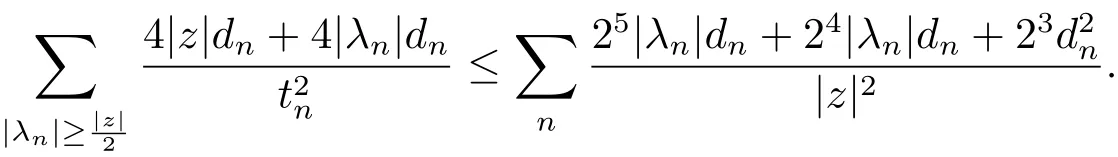
Thus combine with(2.6),(2.9)and(2.10),we eventually get the esitmate

whereA=

To conclude the proof,we use the representation(2.4)ofG(z).By Lemma 2.1 and the conditions imposed on Γ,we can define a functionG1(z)in the form of(2.4),

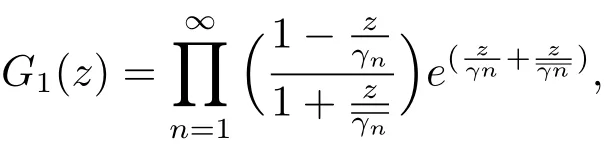
which is analytic in the right half-plane C+and vanishes exactly on the sequence Γ ={γn:n=1,2,···}.According to(2.11),estimate(2.5)is satisfied forG(z)andG1(z).

We now get ready to prove Theorem 2.1.

Proof of Theorem 2.1 In order to prove M(Λ)and M(Γ)are complete or incomplete inCαsimultaneously,it suffces to prove that incompleteness of any of the two systems implies incompleteness of the other.To achieve this,we recall the proof in[1].

We assume that M(Λ)is incomplete inCα.From[1],we know that the incompleteness of M(Λ)inCαis equivalent to the existence of a non-trivial functiong(z)analytic in the right half-plane C+,which vanishes on some sequence Υ⊇Λ and is defined by

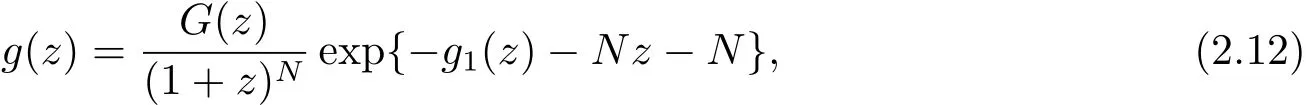
whereNis a large positive integer,G(z)is defined by(2.4),andg1(z)is analytic in the right half-plane,satisfying

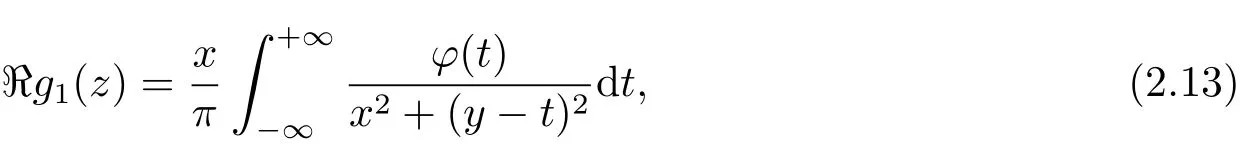
ϕ(t)is an even function such thatϕ(t)=α(λΛ(t)−a)for somea∈R and allt≥0,whereλΛ(t)is defined in Lemma 2.1.

Suppose(2.3)is satisfied for some complex sequences Γ with(2.1)and(2.2)imposed.By(2.10),we know that we can find a non-trivial analytic in the right half-plane whose real part is defined in(2.13).ReplaceG(z)withG1(z)which is defined in Proposition 2.1,we can get a function analytic in the right half-plane,which vanishes on Γ and satisfies(2.12),wherever the functionλΓ(t)defined in Lemma 2.1 has the same growth asλΛ(t).This implies the incompleteness of M(Γ)inCα.

3 The Exponents with Multiplicity

In this section,we will consider the stability problem wherever the exponent is a positive multiplicity sequencehereµn→∞is allowed.We need some definitions and auxiliary results from[11].

Definition 3.1 If a real positive sequence A={an}satisfies for some positive constantcthe spacing conditionan+1−an≥cfor alln≥1 and=D≥0,then we say it belongs to the class L(c,D).

Definition 3.2 Let the sequence A∈L(c,D)andα,βbe real positive numbers such thatα+β＜1.We say that a sequencewith real positive termsbn,not necessarily in an increasing order,belongs to the class Aα,βif for all n∈N,we have

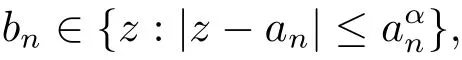
and for allm/=none of the following holds

(i)bm=bn.

(ii)|bm−bn|≥

We may write B in the form of a multiplicity sequenceby grouping together all those terms that have the same modulus,and ordering them so thatλn＜λn+1,this form of B is called as{λ,µ}reordering(see[11]).

Theorem 3.1 Letα(t)be a nonnegative convex on R satisfying(1.1).Suppose two sequences of positive numbers Λ =andare{λ,µ}reordering of two positive sequence defined in Definition 3.1 and Definition 3.2,furthermore,suppose there exist a decreasing functionβ:[0,+∞)→(0,+∞)and a positive sequence{tn}that is linked with the sequences such that

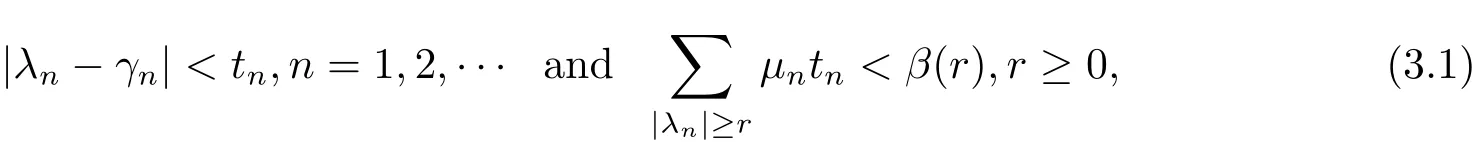
then M(Λ)and M(Γ)are complete or incomplete inCαsimultaneously.

Before we prove Theorem 3.1,we should establish a proposition which is similar to Proposition 2.1.And we will use the following result from[11].

Lemma 3.1(see[11])Let A∈L(c,D),B∈Aα,βand Λ =be its{λ,µ}reordering.Then the function

is analytic in the right half-plane C+,and vanishes exactly on the sequence Λ =Withr=|z|andx=ℜz,for some positive constantA,we have

whereσΛ(r)=The following proposition is a modified version of Proposition 2.1.

Proposition 3.1 LetG(z)be a function analytic in the right half-plane C+which is defined in(3.2)and vanishes exactly on the sequencewhich is the{λ,µ}reordering of some positive sequence defined in Definition 3.1 and Definition 3.2.Given a decreasing functionβ:[0,+∞)→(0,+∞),we can find a functionG1(z)analytic in the right half-plane C+with the sequence of zeros Γ =which is the{λ,µ}reordering of a positive sequence satisfying Definition 3.1 and Definition 3.2,furthermore,we can find a positive sequence{tn}that is linked with the sequence such that(3.1)is satisfied and for

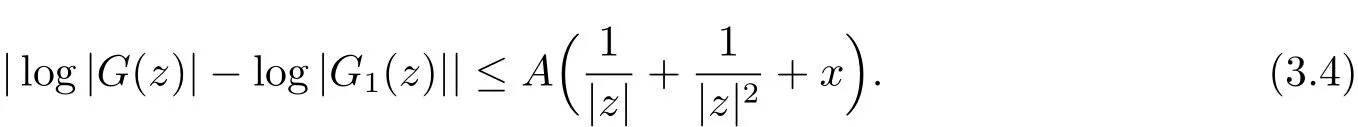
Proof The proof is a modification of the one for Proposition 2.1.By the properties of the zeros ofG(z),we can choose a sequence of strict positive numbers{tn}such that the disksD(λn,tn)are mutually disjoint and(3.4)is satisfied.We can also select strict positive numberdnsuch that

We will estimate the sum of differencesz∈(λn,tn),

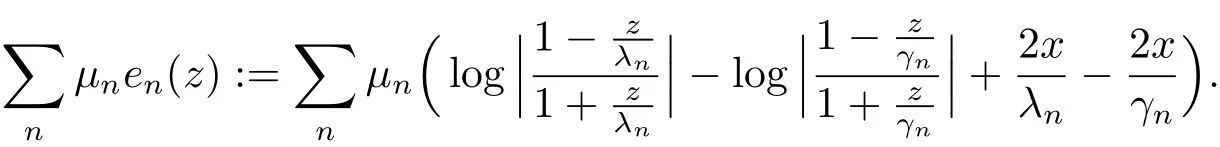
An upper bound foren(z)is obtained as follows:

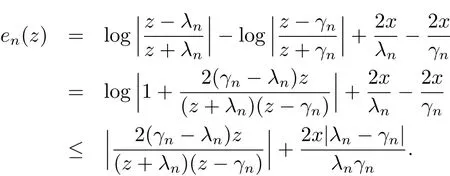
Forz∈C+andλn＞0,we have|z+λn|≥|z−λn|.If we choose a positive sequence 2dn≤tn,then|z− γn|≥|z−λn|−|γn−λnthus

A similar upper bound for−en(z)is also obtained in the following estimate

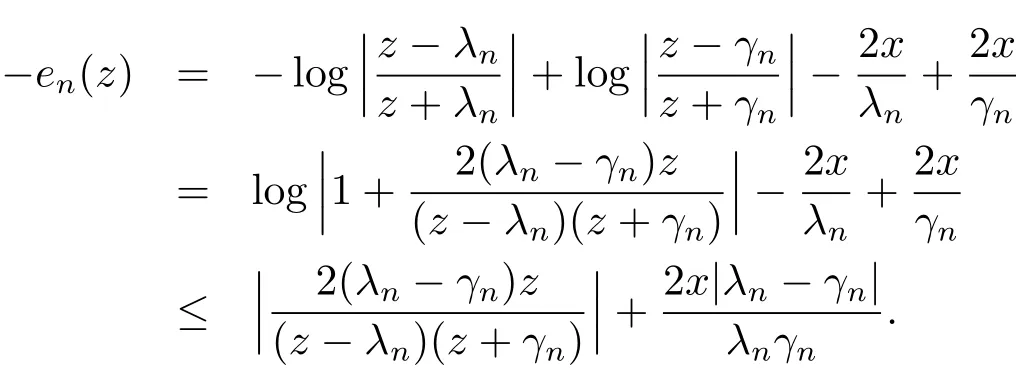
Forz∈C+andγn＞0,we have|z+γn|≥|z−γn|.If we choose a positive sequence 2dn≤tn,then|z−γn|≥|z−λn|−|γn−λn|thus

By(3.6)and(3.7),for allz∈(λn,tn),

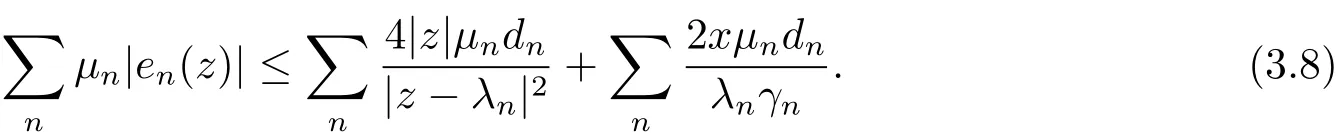
By(3.5),we have

The first term in(3.8)can be estimated as follows

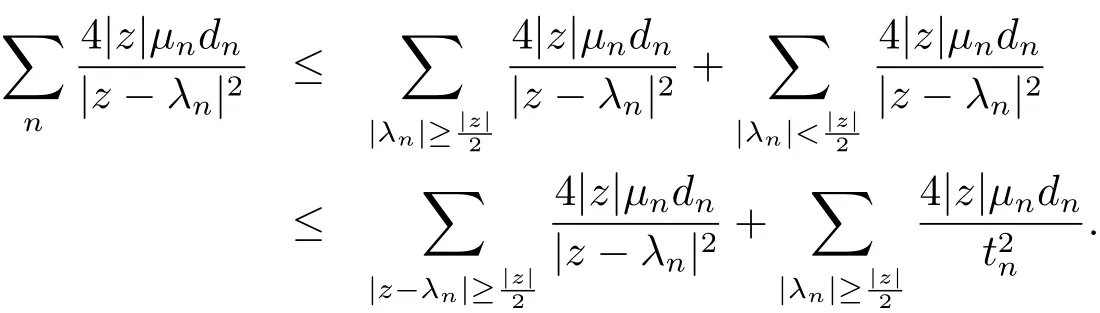
By

(3.8)and(3.9),we have

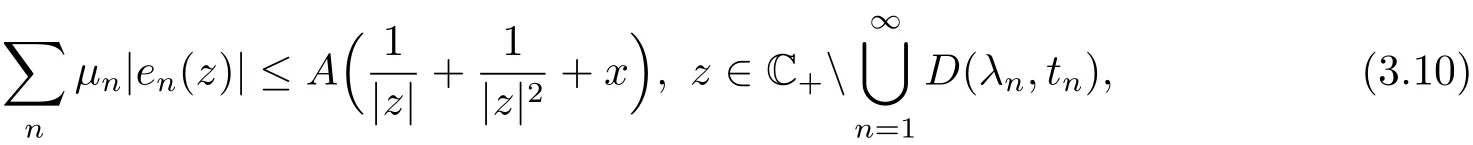
whereA=

To conclude the proof,we use representation(3.2)ofG(z).By Lemma 3.1 and the conditions imposed on Γ,we can define a functionG1(z)in the form of(3.2)

which is analytic in the right half-plane C+={z=x+iy:x＞0}and vanishes exactly on the sequence Λ ={λn,µn}∞n=1.According to(3.10),estimate(3.4)is satisfied forG(z)andG1(z).

With an application of Proposition 3.1,we can prove Theorem 3.1.The proof of Theorem 3.1 is similar to Theorem 2.1 which is again the proof of the main result in[1].

Proof of Theorem 3.1 To prove M(Λ)and M(Γ)are complete or incomplete inCαsimultaneously,it suffces to prove that incompleteness of any of the two systems implies incompleteness of the other.To achieve this,we just need to repeat the proof in[1]word by word.

We assume that M(Λ)is incomplete inCα.From[1],we know that the incompleteness of M(Λ)inCαis equivalent to the existence of a non-trivial functiong(z)analytic in the right half-plane C+,which vanishes on some sequenceand is defined by

whereNis a large positive integer,G(z)is defined by(3.2),andg1(z)is analytic in the right half-plane,satisfying

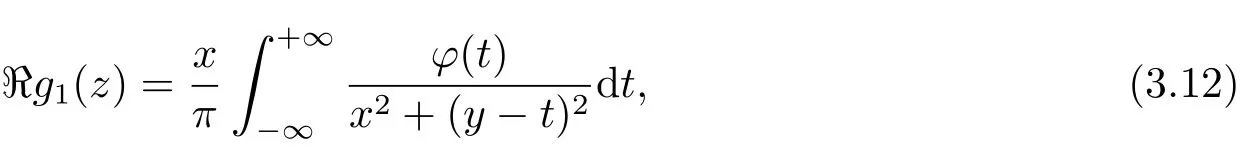
ϕ(t)is an even function such thatϕ(t)=α(σΛ(t)−a)for somea∈R and allt≥0,whereσΛ(t)is defined in Lemma 3.1.

Suppose(3.1)is satisfied for some positive sequence Γ =which is the{λ,µ}reordering of a positive sequence defined in Definition 3.1 and Definition 3.2.By(3.8),we know that we can find a non-trivial analytic in the right half-plane whose real part is defined in(3.12).ReplaceG(z)withG1(z)which is defined in Proposition 3.1,we can get a function analytic in the right half-plane,which vanishes on Γ =and satisfies(3.11),wherever the functionσΓ(t)defined in Lemma 3.1 has the same growth asλΛ(t).This implies the incompleteness of M(Γ)inCα.

[1]Deng G T.Incompleteness and closure of a linear span of exponential system in a weighted Banach space[J].J.Approx.The.,2003,125(1):1–9.

[2]Deng G T.Weighted exponential polynomial approximation[J].Sci.China,2003,46(2):280–287.

[3]Deng G T.On weighted polynomial approximation with gaps[J].Nagoya Math.J.,2005,178:55–61.

[4]Deng G T.Incompleteness and minimality of complex exponential system[J].Sci.China,2007,50(10):1–10.

[5]Khabibullin B N.Sets of uniqueness in spaces of entire functions of a single variable[J].Math.USSR Izvestiya,1992,39(2):1063–1084.

[6]Khabibullin B N.Completeness of sets of complex exponentials in convex sets:open problems,proceeding of the NATO advanced study institute[J].Math.Phys.Chem.,2001:371–373.

[7]Khabibullin B N.Stability of completeness for exponential systems on compact convex sets in C[J].Math.Notes,2002,72(3):542–550.

[8]Khabibullin B N.An approximation theorem for entire functions of exponential type and the stability of zero sequences[J].Mat.Sb.,2004,195(1):143–156.

[9]Khabibullin B N.Spectral synthesis for the intersection of invariant subspaces of holomorphic functions[J].Mat.Sb.,2005,196(3):119–142.

[10]Kudasheva E G,Khabibullin B N.Variation of subharmonic function under transformation its Rieze measure[J].www.math.bsunet.ru/khb-e,2007.

[11]Zikkos E.Completeness of an exponential system in weighted Banach spaces and closure of its linear span[J].J.Approx.The.,2007,146(1):115–148.

[12]Sedletskii A M.Nonharmonic analysis[J].J.Math.Sci.,2003,116(5):3551–3619.

[13]Sedletskii A M.Fourier transforms and approximations[M].Russia:Gordon and Breach Science Publishers,2000.

[14]Yang X D.Incompleteness of exponential system in the weighted Banach space[J].J.Approx.The.,2008,153(1):73–79.

[15]Zhang Y H,Deng G T.Growth properties of generalized Poission integral in the half space[J].J.Math.,2013,33(3):473–478.