基于两级信用支付的两货栈订购策略研究
2018-01-15袁兰兰
张 冲,袁兰兰
(南京邮电大学 管理学院,江苏 南京 210023)
1 引言
信用支付(延期支付)是现代商业活动中常见的一种短期商贷方式,在发达国家的企业融资中起着重要的作用。上游供应商为了提高其商品的市场占有率,可以采用信用支付方式去鼓励下游零售商更多购买其商品。在延期支付期限内,零售商无需向供应商支付任何费用,还可用销售产品收入去获得其他投资收益,超过信用支付期时,零售商需要为未销售商品支付货款和货款利息。Goyal[1]首先提出在信用支付条件下的EOQ模型,随后,众多学者从多个角度(比如需求率变化、允许缺货、变质品等)对Goyal的模型进行了拓展研究,使其研究问题更接近实际情况。
现有文献中,部分文献将信用支付期限设为定值,部分文献考虑信用支付期限不再固定,比如考虑信用支付期与订货量相关。在假定顾客需求不变情况下,Huang[2]探讨了一种新的信用支付模型,假设当订购批量大于某一阈值时,零售商的所有货款均可在信用支付到期时支付。当订购批量小于订购阈值时,零售商需要在货物到库时立即支付部分货款,剩余货款需要在信用支付期内支付。研究发现,信用支付比例较高会导致更高的订购批量和较低的总成本,随着订购阈值增大,零售商订购批量和总成本增加。随后,Chen等[3]对Huang[2]模型中的假设条件进行了部分修正,同时采用一种简单方法对模型进行求解,得到了一些管理启示。假设供应商根据零售商订购批量允许其延期支付货款的同时,零售商也允许下游顾客延期支付货款的情形下,Kreng和Tan[4]研究了信用支付期依赖于订购量的零售商最优库存策略,研究表明,零售商可以采用减少订购批量,增大订购次数的方式来享受信用支付的优惠策略。在两级信用支付策略的条件下,姚云飞等[5]研究基于顾客需求的大小而提供不同等级信用支付期的零售商最优库存策略问题。Chung[6]构建了基于部分信用支付期的变质品EOQ模型。在假设供应商提供给零售商的信用支付期依赖于其订购量的情况下,Ouyang等[7]探讨了下层信用支付期小于上层信用支付期的两层信用支付最优订货策略模型。考虑上层部分信用支付与下层部分信用支付的情况下,杜文意等[8]研究了变质品的三阶段EOQ策略模型。Shah[9]探讨了当零售商的订单超过某一阈值时,供应商提供给零售商现金折扣或者一个固定的信用支付期限的优惠策略问题,研究结果表明,零售商可以在信用支付和价格折扣之间进行权衡,选择利润增加较大的优惠方式。张冲[10]构建基于信用支付的两种支付时间选择模型,研究了不同金融环境下的零售商支付时间选择问题和最优订购策略。
现实中,零售商经营规模有限,自有库存容量受到限制。在这种情况下,为了享受更多的信用支付优惠,零售商有可能租赁仓库,将超出自有库存容量的商品放入其中,此类信用支付问题被归为两货栈库存模型研究。Jamal等[11]首先研究了自有库存有限的信用支付订货策略。随后,在两层信用支付策略下,Chung和Huang[12]研究了库存容量有限的变质品零售商最优策略模型。研究表明,随着变质率增加,零售商会减低订购批量同时导致总成本的增加;随着自有库存的容量越大,零售商会增大订购批量同时降低其总成本。在不限制利息支出率与利息收益率大小的条件下,Teng[13]探讨了库存容量有限的两层信用支付EOQ模型。在允许延期支付的条件下,闵杰和常浩[14]构建了一种变质品的两货栈的零售商库存模型。Yen等[15]构建了基于信用支付和有限库存容量的零售商最优订购策略。在两层信用支付策略的条件下,Liao[16]探讨了库存容量有限的变质品最优订货策略。零售商可以根据不同金融条件下的利息收入率与利息支出率的不同,来决定何时支付货款。
在现有的文献中,信用支付模型考虑了信用支付期限与订货量相关的情形,却忽略了一个重要的实际问题,都假设不管订购批量大小,零售商总能把它们存放在自有仓库中。而事实上,零售商的决策会受到自有库存容量的限制。即当两级信用支付存在时,零售商为了享受更多优惠有可能加大订货量,这时不得不考虑自有库存容量限制,以及是否通过租赁仓库来存储超出自有库存容量的商品。因此,在考虑供应商根据零售商订单的大小提供两级信用支付期条件下,本文研究了零售商自有库存有限条件下的EOQ模型,以零售商的年平均相关成本最小化为目标,证明了零售商最优订货周期的存在且唯一,最后通过算例来进一步验证模型和求解方法的有效性,提出了一些管理启示。
2 符号与假设
本模型需要的符号表示如下:D为顾客需求率,是确定值;p为零售商销售单位商品的价格;c为零售商采购单位商品的价格;h为零售商自有仓库内单位商品单位时间的仓库保管费用(不包含仓库商品占用资金的成本);k为零售商租赁的仓库内单位商品单位时间的库存保管费用(不包含仓库商品占用资金的成本);s为零售商一次订货的固定订货费用;A为租赁仓库的固定费用;Ic为单位库存商品单位时间的利息支出率;Ie为单位库存商品单位时间的利息收益率;W为零售商自有仓库的库存容量;W1为供应商提供给零售商延期支付期限M1时的允许最小订购数量(订货阀值);W2为供应商提供给零售商信用支付期限M2时的允许最小订购数量(订货阀值),且W1<W2,M1<M2;Q为零售商的订货批量;Q*为零售商的最优订货批量;T为零售商的订购周期,为决策变量;T*为零售商的最优订购周期;tw为零售商租赁仓库内商品售完所需时间,即tw=(Q-W)/D;Ta为零售商自有仓库内商品售完所需时间,即Ta=W/D;Tw1为订购量W1售完所需时间,即Tw2为订购量W2售完所需时间,即为零售商的年平均成本;TC(T*)为零售商的年平均成本最小值。其中,OW表示自有仓库,RW表示租赁仓库。
本模型假设如下:(1)不允许缺货;(2)顾客需求率为定值;(3)库存系统运行时间无界;(4)供应商允许零售商延迟支付的期限小于零售商的补货周期,即M2<T;(5)为计算方便,假设cIc>pIe;(6)当Q<W1时,表示零售商需要在订购时支付货款,不享受信用支付优惠,当W1≤Q<W2时,表示零售商可以在信用支付期M1时支付货款,当Q≥W2时,表示零售商可以在信用支付期M2时支付货款;(7)零售商根据顾客需求,优先出售租赁仓库中的商品,然后出售自有仓库中的商品。
3 数学模型的构建
零售商的年总费用由年采购费、年订货费、自有库存持有费、租赁库存固定费、租赁库存持有费、年利息收支等组成。而各项费用因Ta、Tw1和Tw2三者之间的大小关系不同而变化。因此,依据三者之间的大小关系,将分为三种情形进行讨论。
3.1 情形1 Ta>Tw2>Tw1
(1)年订货费用=s/T
(2)年采购费用=cD
(3)RW的年租金和库存费用
情形①T≤Ta,不需要租赁仓库,因此不产生租金和库存费用。
情形②T>Ta,RW的年租金=A/T,
(4)OW的年库存费用
情形①:T≤Ta,OW的年库存费用=hDT/2;
情形②:T>Ta,OW的年库存费用=hW(T+tw)/(2T)。
(5)年利息支出
情形①:0<T<Tw1,年利息支出=cIc DT/2;
情形②:Tw1
≤T<Tw2,
情形③:T≥Tw2,
(6)年利息收入
情形①:0<T<Tw1,小于订货阀值W1,不享受信用支付优惠,无利息收入;
情形②:Tw1≤T<Tw2,
情形③:T≥Tw2,
由上可知,零售商的年平均费用=一次订货的固定订货费用+年订货费+自有库存存储费用+租赁库存固定费+租赁库存存储费用+年利息支出-年利息收入,即:

3.2 情形2 Tw2>Ta>Tw1
在这种情形下,零售商的年平均费用为:

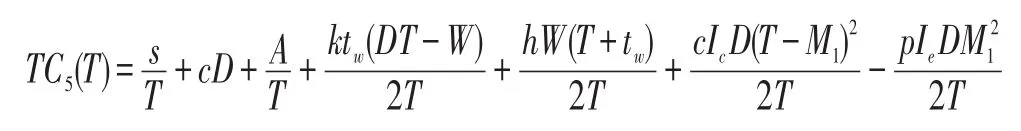
3.3 情形3 Tw2>Tw1>Ta
在这种情形下,零售商的年平均费用为:

4 模型求解
4.1 情形1 Ta>Tw2>Tw1
为研究方便,不妨将TC1(T)的定义域延拓为(0,+∞),对TC1(T)求导可得:

为研究方便,不妨将TC2(T)的定义域延拓为(0,+∞),对TC2(T)求导可得:

为研究方便,不妨将TC3(T)的定义域延拓为(0,+∞),对TC3(T)求导可得:

为研究方便,不妨将TC4(T)的定义域延拓为(0,+∞),对TC4(T)求导可得:

因此,对于Ta>Tw2>Tw1的情形,零售商年平均费用函数TC(T)的最优解为T*=argmin{T1*,T2*,T3*,T4*},即TC(T)在(0 ,+∞)上的最优值为TCi(T)(i =1,2,3,4)在各自区间上最优值的最小值。
4.2 情形2 Tw2>Ta>Tw1
由情形1求解过程可知,TC1(T)在[Tw2,+∞ )上的最优解为T1*=max{T1, Tw2}。
为研究方便,不妨将TC5(T)的定义域延拓为(0,+∞),对TC5(T)求导可得:

由情形1求解过程可知,TC3(T)在[Tw1,Ta]上的最优解可通过如下方式确定:若T3≤Tw1,则;若Tw1<T3<Ta,则 T3*=T3;若 T3≥Ta,则
由情形1求解过程可知,TC4(T)在(0 ,Tw1)上的最优解T4*=min{T4, Tw1}。
因此,对于Tw2>Ta>Tw1的情形,零售商年平均费用函数TC(T)的最优解为T*=argmin{T1*,T5*,T3*,T4*},即TC(T)在(0 ,+∞)上的最优值为TCi(T)(i=1,5,3,4)在各自区间上最优值的最小值。
4.3 情形3 Tw2>Tw1>Ta
由情形1求解过程可知,TC1(T)在[Tw2,+∞ )上的最优解为T1*=max{T1, Tw2}。
由情形2求解过程可知,TC5(T)在[Tw1,Tw2)上的最优解T5*可通过如下方式确定:若T5≤Tw1,则;若Tw1<T5<Tw2,则T5*=T5;若 T5≥Tw2,则
为研究方便,不妨将TC6(T)的定义域延拓为(0,+∞),对TC6(T)求导可得:
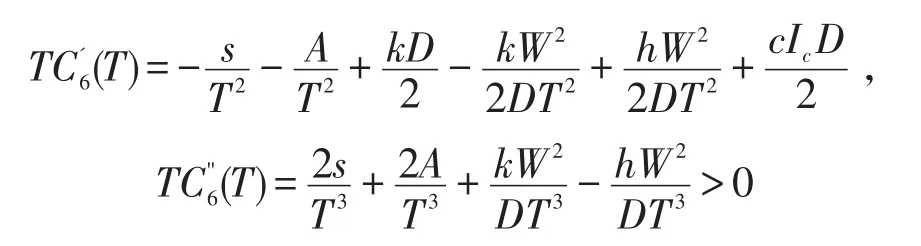
由情形1求解过程可知,TC4(T)在区间(0 ,Ta)上的最优解T4*=min{T4, Ta}。
因此,对于Tw2>Tw1>Ta的情形,零售商年平均费用函数TC(T)的最优解为T*=argmin{T1*,T5*,T6*,T4*},即TC(T)在区间(0 ,+∞ )上的最优值为TCi(T)(i=1,5,6,4)在各自区间上最优值的最小值。
5 算例仿真
以下举例说明本文所建模型和相关理论,探讨一些相关参数的变化对于零售商是否租用库存以及年平均费用最小值的影响。
例1 假定需求系数D=3 300(单位/年),一次订货的固定费用s=150(元),自有仓库商品保管费用h=0.6(元/单位/年),租赁仓库商品保管费用 k=0.8(元/单位/年),租赁仓库的固定费用 A=120(元),零售商购买单位商品的价格c=5(元/单位),零售商销售单位商品的价格 p=10(元/单位),利息收益率Ie=0.02(元/单位/年),利息支付率 Ic=0.08(元/单位/年),自有仓库容量W=1 500(单位),W1=800(单位),M1=0.15年,W2=1 300(单位),M2=0.2年。通过计算得到满足情形1的条件,即满足Ta>Tw2>Tw1,T1*=0.455,T2*=0.394,T3*=0.309,T4*=0.242。通过比较可知,T*=T2*=0.394(年),Q*=1 300(单位),并且有TC(T*)=TC(T2*)=17 300.277(元)。
根据算例1的参数设定,进一步分别探讨了重要参数W、Ic、k,s、c的变化对零售商最优订货策略(最优订购周期、最优订购批量、最低平均费用以及是否租用库存)的影响。表1-表5为参数变化对零售商订购策略的影响。
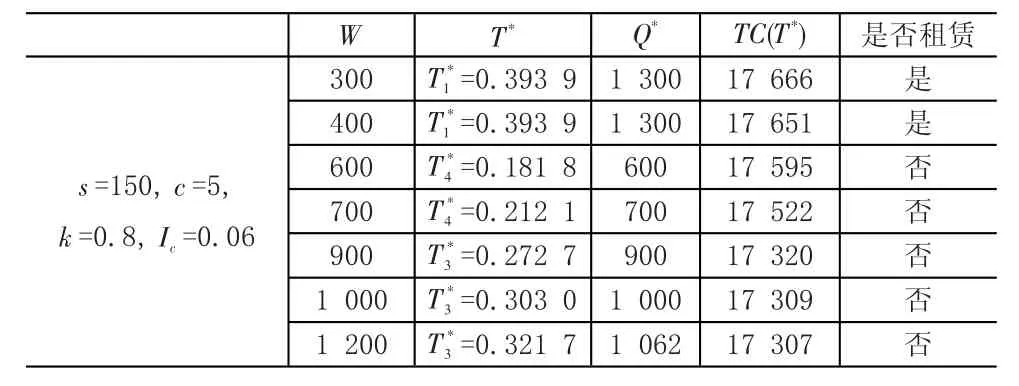
表1 W的变化对零售商订购策略的影响
当自有仓库容量W较小时,零售商的最优订购周期T*保持不变,而其订购批量较大,零售商租用库存的决策为“是”。说明零售商为了获得信用支付所带来的收益,会增加其订购批量,进而将租用库存。随着自有仓库容量W的增加,零售商的最优订货周期T*变大,年平均费用TC(T*)随之减少,零售商租用库存的决策为“否”。说明在顾客需求D不变的情况下,当自有仓库容量增加时,零售商更加倾向于将商品存放在自有库存中,选择租赁库存的概率必然降低,年费用支出也相应减少。此算例表明,零售商应在能力范围内积极拓展自有库存容量,以求增加订购周期,降低订购批量,最终降低年平均费用。

表2 Ic的变化对零售商订购策略的影响
当单位库存单位时间的支付利息Ic增加时,最优年平均费用TC(T*)增加,在利息收益率与支出率相差不大时,零售商的最优订购周期T*保持不变,此种情形下,零售商不需要租用库存。当利息支出率较高时,零售商将增大订购周期,同时提高订购批量,进而零售商需租用仓库以存储更多的商品。随着利息支出率的提高,零售商最优订货周期T*减小,零售商租用仓库的决策为“是”。说明利息支出率越高,零售商的年平均成本增加,此时零售商应该尽量减少其订购批量,以达到更频繁的减少信用支付利息的目的,减少年平均成本的增长率。

表3 k的变化对订购策略的影响
当租赁库存单位商品单位时间的库存保管费用k增加时,零售商的最优订货周期T*减少,而年费用TC(T*)增加,零售商租用库存的决策从“是”变为“否”。这也就意味着,在信用支付条件下,租赁仓库的库存保管费用越高成本越高。所以此时应选择更少的订货量,从而避免订单量过大不得不租赁库存的现象发生。
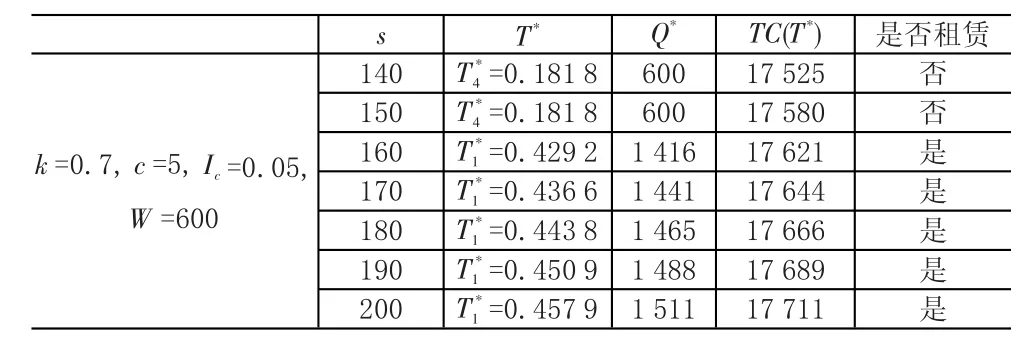
表4 s的变化对零售商订购策略的影响
随着零售商一次订货的固定费用s增加,其年费用TC(T*)也随之增大。当一次订货的固定费用较低时,零售商的最优订购周期T*不变,零售商租用仓库的决策为“否”;之后,随着固定订货费用的增加,零售商最优订货周期T*增大,零售商租用库存的决策为“是”。此种情况说明,随着零售商固定订货费用的增大,为了分摊固定成本过高的压力,零售商在权衡利弊下更加倾向于扩大订单量,并将多余的商品存放在租赁仓库中。

表5 c的变化对零售商订购策略的影响
随着单位商品购买费用c的增大,零售商年平均费用TC(T*)增大。当单位商品的购买费用较低时,零售商的最优订购周期T*=0.181 8保持不变,零售商租用库存的决策为“否”;之后,随着购买费用的增加,零售商最优订货周期T*=0.393 9保持不变,零售商租用库存的决策为“是”,这也就意味着,单位商品的购买费用越高,零售商所应支付的商品成本增加,相应的年费用随之增加,为了取得同样多的收益,不得不扩大订单量,并将多余的商品存放在租赁仓库中。
6 结语
在假定供应商根据零售商的订购批量大小提供两级信用支付期的情况下,讨论了零售商是否租用仓库的两货栈库存模型,分别对模型中三种可能情形进行讨论,提出了求解算法,并给出了证明,最后通过算例验证了模型和理论结果的有效性。研究表明,零售商的年平均费用的最小值随着自有仓库容量W增大而减小,零售商应该积极拓展自有库存容量;随着租赁仓库内单位商品单位时间的库存保管费用k的增大,零售商最优订货周期减小,年平均费用增高。作为应对措施,零售商应该选择增大订货频率,降低每次的订货批量,由此降低年平均费用;随着单位时间单位库存的支付利息Ic、零售商一次订货的固定费用s和单位商品的购买价格c的增大,零售商租用仓库的决策从“否”变为“是”,也就意味着,不同的参数组合,零售商需在降低年平均费用的前提下,选择是否租用仓库。
虽然本文对现有的相关库存模型进行了推广,但在一些假设方面有所欠缺,比如本文考虑确定的顾客需求率,而现实中顾客需求依赖于库存水平、营销努力水平。模型中还可以进一步考虑到允许缺货以及产品的变质等情况,为现实生活中的订货策略提供更好的指导意义。
[1]Goyal S K.Economic order quantity under conditions of permissible delay inpayments[J].Journal of the Operational Research Society,1985,36(4):335-338.
[2]Huang Y F.Economic order quantity under conditionally permissible delay in payments[J].European Journal of Operational Research,2007,(176):911-924.
[3]Chen S C,Cárdenas-Barrón L E,Teng J T.Retailer’s economic order quantity when the supplier offers conditionally permissible delay in payments link to order quantity[J].International Journal of Production Economics,2014,(155):284-291.
[4]Kreng V B,Tan S J.The optimal replenishment decisions under two levels of trade credit policy depending on the order quantity[J].Expert Systems With Applications,2010,37(7):5 514-5 522.
[5]姚云飞,郝家芹,张亚东.二层信用支付下顾客细分的库存模型[J].应用数学,2013,26(4):791-797.
[6]Chung K J.The EOQ model with defective items and partially permissible delay in payments linked to order quantity derived analytically in the supply chain management[J].Applied Mathematical Modelling,2013,37(4):2 317-2 326.
[7]Ouyang L Y,Yang C T,Chan Y L,et al.A comprehensive extension of the optimal replenishment decisions under two levels of trade credit policy depending on the order quantity[J].Applied Mathematics and Computation,2013,224:268-277.
[8]杜文意,艾兴政,刘晓婧,等.基于部分延迟支付期限的易损品经济批量订货模型研究[J].管理工程学报,2014,28(3):209-217.
[9]Shah N H.Retailer’s decision for ordering and credit policies for deteriorating items when a supplier offers order-linked credit period or cash discount[J].Applied Mathematics&Computation,2015,259:569-578.
[10]张冲.基于信用支付的零售商最优订购策略选择研究[J].软科学,2016,30(3):140-144.
[11]Jamal A M M,Sarker B R,Wang S.An ordering policy for deteriorating items with allowable shortages and permissible delay in payment[J].Opsearch,2007,1(1):152-159.
[12]Chung K J,Huang T S.The optimal retailer’s ordering policies for deteriorating items with 1imited storage capacity under trade credit financing[J].International Journal of Production Economics,2007,106(l):127-145.
[13]Teng J T,Chen J,Goyal S K.A comprehensive note on:An inventory model under two levels of trade credit and limited storage space derived without derivatives[J].Applied Mathematical Modelling,2009,33:4 388-4 396.
[14]闵杰,常浩.两货栈及允许延期付款情形下变质性商品的最优订货策略[J].系统工程理论与实践,2009,29(3):90-99.
[15]Yen G F,Chung K J,Chen T C.The optimal retailer's ordering policies with trade credit financing and limited storage capacity in the supply chain system[J].International Journal of Systems Science,2012,43(11):2 144-2 159.
[16]Liao J J,Huang K N,Ting P S.Optimal strategy of deteriorating items with capacity constraints under two-level of trade credit policy[J].Applied Mathematics and Computation,2014,233:647-658.
