多态系统可靠性分析广义灰色贝叶斯网络模型
2018-01-15曹颖赛刘思峰方志耕
曹颖赛, 刘思峰, 方志耕, 张 秦
(南京航空航天大学经济与管理学院, 江苏 南京 211106)
0 引 言
随着系统功能和结构的不断复杂化,其性能状态逐渐呈现出一定的多样性和依赖性,即系统在正常工作和彻底失效两种极端状态之间还存在多种不同的性能状态。自文献[1]涉足该类系统的可靠性分析以来,众多研究学者相继投入到了该领域,并累积了丰富的研究成果,最近的学术探索包括:
文献[2]针对多态系统性能状态种类多、部件数量大等特点,提出了一种扩展型多变量布尔逻辑函数,从而解决了传统结构函数进行系统特征描述时所面临的组合爆炸难题。文献[3]构建了一种广义通用生成函数模型,并利用Z变换求得了多态系统的可靠度函数、平均无故障间隔时间等参数,为离散型多态系统的可靠性评估问题提供了较完整的解决方案。文献[4]采用蒙特卡罗仿真技术以及相关迭代算法得出了多状态加权k-out-of-n表决系统的一系列可靠性特征参数。文献[5]针对可修多态系统提出了瞬时可用度概念,并利用随机过程与通用生成函数相结合的方法,构建了可修多态系统瞬时可用度和平均瞬时性能残差测度模型。文献[6]提出了一种基于系统性能状态转移概率的系统可靠性迭代评估算法,并将其应用至多状态贮备系统可靠性分析中。
上述方法虽然能够为多态系统可靠性分析提供一些解决方案,但仍存在一定方法本身所固有的缺陷。布尔模型扩展方法分析过程较复杂、计算繁琐,在很大程度上限制了其在大型复杂多态系统中的应用。随机过程理论虽然能够便捷地处理多态系统可靠度与时间的变化关系,但其要求系统各状态的驻留时间必须服从指数分布且当部件数量或状态较多时其分析计算量将呈现爆炸式增长。蒙特卡罗仿真难以获得系统可靠度精确解且需要大量的数值模拟才能够获得相对准确的分析结果。通用生成函数方法通常仅针对离散单一的随机变量,对于具有多性能参数的部件和系统可靠性分析难以为继。
为了寻找更加切实可行的多态系统可靠性分析工具,国内外学者纷纷聚焦于贝叶斯网络[7],因为贝叶斯网络在表达和分析不确定性系统以及逻辑关系双向推理等方面的优势正好契合了多态系统的可靠性分析需求。具有代表性的学术文献包括:文献[8]构建了一种基于贝叶斯网络的离散多状态系统剩余寿命评估模型。文献[9]运用贝叶斯网络求解了多态系统状态之间的转移概率并对系统组成部件进行了重要性分析。文献[10]针对系统或部件状态数量较多时出现的组合爆炸问题,提出了一种动态贝叶斯网络模型。文献[11]运用贝叶斯网络混合算法,解决了既包含离散变量又含有连续变量的系统可靠性评估问题。此外,文献[12]针对多状态流网络的可靠性评估问题,提出了新的贝叶斯网络建模与推理算法。
然而,随着现代科技的迅速发展和人们日益增长的高技术含量、高复杂度产品需求,复杂产品越来越普遍地存在于社会的各个领域,但多品种小批量的生产方式和独特的服务模式为此类产品的可靠性分析带来了众多不确定因素,致使上述基于确定数据信息的系统可靠性分析方法很难继续发挥作用。文献[13]通过将贝叶斯网络与模糊数学相结合,构建了一种针对不确定性多态系统的可靠性分析模型。文献[14]针对传统可靠性分析方法在处理不确定性信息方面的不足,构建了一种基于区间三角模糊数的贝叶斯网络模型。文献[15]运用一种能够融合专家先验信息与试验数据的贝叶斯网络模型,求得了多态系统的可靠度后验分布,并采用模拟仿真的方法验证了所得结果的正确性。文献[16]针对系统可靠性参数难以精确测定的问题,将传统贝叶斯网络模型进行了改进并融合了直觉模糊的概念,有效拓展了贝叶斯网络处理不确定性问题的能力。
综上,基于贝叶斯网络的多态系统可靠性分析模型虽然历经多年的发展取得了丰富的研究成果,但对于现实中复杂多态系统的可靠性分析仍有所欠缺。具体待改进之处为:①运用模糊子集表征节点的故障状态或故障率,虽然能解决某些不确定条件下的多态系统可靠性分析问题,但简单地用定值表示模糊子集元素,往往会造成部分重要信息丢失,致使系统可靠性分析结果出现偏差;②目前基于贝叶斯网络的多态系统可靠性分析模型都是以确定的故障逻辑关系作为前提条件的,然而由于相关历史数据的缺乏、系统使用环境的变化以及其他人为因素的影响,系统与部件间的故障逻辑关系往往很难以确定的形式呈现;③传统的可靠性分析贝叶斯网络模型往往仅针对单一种类的不确定性影响因素,其处理不同逻辑视角的多种不确定性因素的能力亟需拓展。
针对以上问题,本文提出了一种多态系统可靠性分析广义灰色贝叶斯网络模型,运用含有区间灰数的模糊子集表征部件的故障状态,用区间灰数表示部件与系统之间的故障发生条件概率,在为不确定背景下的多态系统可靠性分析提供理论指导的同时,也提升了贝叶斯网络处理多种不确定性因素的能力。
1 系统可靠性分析贝叶斯网络
1.1 基于贝叶斯网络的二态系统可靠性分析
对于一个二态系统而言,系统要么正常工作要么完全失效。根据布尔真值法,可以用“0”表示部件或系统正常工作,“1”表示部件或系统完全失效。在运用贝叶斯网络进行二态系统可靠性分析时,系统组成单元对应为贝叶斯网络的根节点,子系统对应为中间节点,系统对应为叶节点(见图1和图2)。

图1 并联系统贝叶斯网络转换关系示意图Fig.1 Diagram of Bayesian network transformation forparallel system
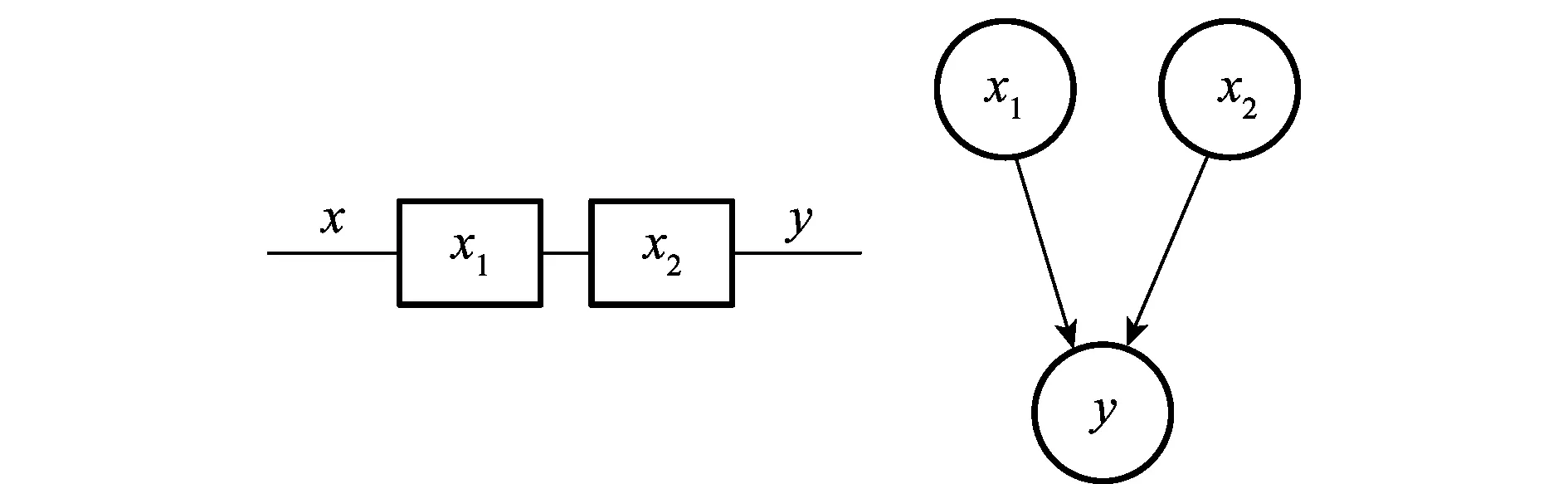
图2 串联系统贝叶斯网络转换关系示意图Fig.2 Diagram of Bayesian network transformation for series system
网络中各节点有且仅有两种状态且在给定父节点状态的情况下,子节点处于各个性能状态的条件概率之和为1(见表1和表2)。

表1 并联系统条件概率表

表2 串联系统条件概率表
1.2 基于贝叶斯网络的多态系统可靠性分析
传统的二态系统在突发型失效的假设下仅仅将系统和部件描述为正常和失效两种性能状态。但随着现代科学技术的迅速发展和工业制造水平的不断提高,产品寿命逐渐变长、可靠性水平日益提高,产品的失效方式大都呈现为退化失效,因此系统在完全正常和失效之间还存在着多种故障模式和不同的故障状态。传统的可靠性分析方法(包括可靠性框图、二元决策图以及故障树等)只能表达部件或子系统间确定的故障逻辑关系,即只能判断在部件正常工作和完全故障时系统的可靠性状态,对于具有多种性能状态的系统可靠性分析往往难以为继。贝叶斯网络能够通过改变子节点条件概率表赋值的形式,方便地表征部件和系统的多种故障状态(见图3和表3)。

图3 多态系统贝叶斯网络示意图Fig.3 Diagram of Bayesian network for multi-state system

x1x2P(y=0|x1,x2)P(y=0.5|x1,x2)P(y=1|x1,x2)000.80.10.100.50.150.650.2010.10.20.7︙︙︙︙︙110.020.080.9
值得注意的是,贝叶斯网络还能表征部件和系统之间不确定性的故障逻辑关系。如表3中P(y=0.5|x1=0,x2=0)=0.1表示在系统组成单元都正常工作的情况下,系统的可靠性退化至0.5态的概率为0.1,在工程实际中可表示为由其他环境因素或人为因素所导致的系统可靠性退化。
2 多态系统可靠性分析广义灰色贝叶斯网络模型构建
虽然贝叶斯网络在系统故障逻辑关系表达与多态可靠性推理方面较传统的可靠性分析模型有了明显的突破与改进,但当系统或部件所处的性能状态以及相互之间的故障逻辑关系具有一定的不确定性时,贝叶斯网络将很难继续发挥其在可靠性分析与建模方面的优势性作用。本节将基于不确定性分析理论,构建新的针对多态系统可靠性分析的贝叶斯网络模型,同时使贝叶斯网络具有处理多种不确定性因素的能力。
根据文献[17],包括模糊关系在内的多种不确定性关系分析皆能统一到灰色集合关系的框架中,因此将本文所提出的既包含模糊子集又含有区间灰数的多态系统可靠性分析贝叶斯网络模型称为广义灰色贝叶斯网络模型。
2.1 多态系统可靠性分析广义灰色贝叶斯网络节点故障状态描述
对于多态系统而言,在系统和部件可靠性退化过程中其各个状态之间的界限并不十分明显,呈现出“亦此亦彼”的特点,具有一定的模糊性。考虑到语言变量在描述模糊概念方面的便捷性与实用性,本部分利用语言变量描述节点不同的故障状态,所采取的模糊概念集合为{完全正常,中间态,完全失效},对应的模糊数分别为0、0.5和1。在构造其他故障状态对于语言值所描述的3种状态的隶属度函数时,由于系统内外扰动因素的存在和人的认知水平局限,不可避免地造成隶属度函数中的某些参数具体信息难以获取,只知道其大致取值范围而无法确定其具体取值。


图4 部件或系统故障状态隶属度函数示意图Fig.4 Diagram of membership function for fault state ofcomponent or system
2.2 多态系统可靠性分析广义灰色贝叶斯网络灰色CPT描述
由于人们对于系统的内部结构、运行行为以及组成元素等参数信息的认知限制以及产品相关历史运行数据缺乏,系统与部件之间的故障逻辑关系往往带有很大程度的灰信息特征。这时如果简单地用定值表示系统与部件之间的故障逻辑关系往往会造成部分重要的可靠性信息丢失,使系统的可靠性分析结果出现偏差。为了更充分地挖掘系统可靠性信息、厘清系统和部件之间的故障逻辑关系,本部分采用区间灰色数⊗ij代替传统贝叶斯网络确定型的条件概率数值,描述部件处于不同故障状态条件下系统处于各个状态的概率。因此对于任一包含两个具有m种状态节点的广义灰色贝叶斯网络,其条件概率表如表4所示。

表4 广义灰色贝叶斯网络灰色条件概率表
3 多态系统可靠性分析广义灰色贝叶斯网络模型求解
本节将采用贝叶斯网络桶消元推理算法[19]测算多态系统可靠性特征参数。作为贝叶斯网络精确推理算法之一,桶消元法旨在通过改变变量消除顺序达到简化计算过程的目的,该方法有效地解决了求解网络中各节点联合概率分布过程中的组合爆炸难题。该算法首先利用网络节点之间的条件独立关系以及链式乘积规则,将各节点的联合概率转化为一系列条件概率的乘积形式;然后为每个节点变量所对应的条件概率函数预设一个“桶”,根据节点之间的条件独立关系及其求解所需的运算量大小,确定消元顺序;最后进行求和、乘积运算以得到待求结果。由于引入了“桶”的概念,因此称之为桶消元法。
3.1 节点故障状态推理

P⊗(T=Tq)=
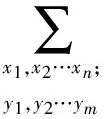

(1)



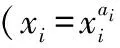
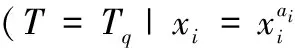
(3)
3.2 节点重要度测算
重要性测度作为灵敏性、风险性的综合定量化体现,是系统可靠性分析的关键环节,是定量分析组成单元对于系统影响程度、确定系统薄弱环节的重要工具之一。合理地确定系统各个组成单元的重要性排序不仅有助于改善系统设计,还能够帮助人们制定合理的故障诊断清单从而提高系统故障诊断效率。
(1) 灰色概率重要度
概率重要度是指当多态系统组成单元xi发生可靠性退化时系统可靠性发生退化的概率,其综合反映了该节点对叶节点故障状态Tq的影响程度。按照这一思路,可将多态系统可靠性分析广义灰色贝叶斯网络节点的灰色概率重要度定义为

(4)

(2)状态重要性测度

)-
P⊗(T=Tq|xi=0)],0}
(5)
3.3 系统可靠性特征参量取值范围分析
当运用包含区间灰数的模糊子集表征节点故障状态,区间灰数表征部件和系统的条件概率数值时,所求得的多态系统可靠性特征参量将是一系列由网络中不确定区间数灰数所组成的映射关系集合。在此为得到这些特征量的最终取值范围,需要基于灰数全局优化算法构建如式(6)所示的系统可靠性特征参量最值求解规划模型。
max (min)R(⊗1,⊗2,…,⊗n)
(6)
对于不同节点可靠性特征参量的大小比较问题,可根据文献[20]提出的基于“势”的区间灰数大小比较方法,通过构建“优势度”“劣势度”等指标综合评判待比较特征量的相对大小。
4 案例研究
某民用航空制造公司针对传统黑匣子无法脱离于机身、事故发生时损坏严重、数据恢复难度较大以及定位困难不利于搜寻等缺陷生产了一种能够视频记录飞行器迫降或失事前飞行器的飞行姿态及其机体外部的破损情况并且能够漂浮于水面的可脱离应急跟踪记录设备。该设备由智能触发系统、设备弹射系统、跟踪记录系统以及设备定位与回收系统4部分组成。作为应急跟踪记录设备的核心子系统,设备弹射系统是该系统中较为复杂的部件之一,由中央控制系统和弹射动力系统组成(见图5)。当弹射临界条件被触发时,舱盖分离系统将在中央控制系统的调控下打开舱盖锁,舱盖随即翻转并由抛盖系统抛至弹射区域经由传动装置和弹射装置最终弹射至缓降系统。
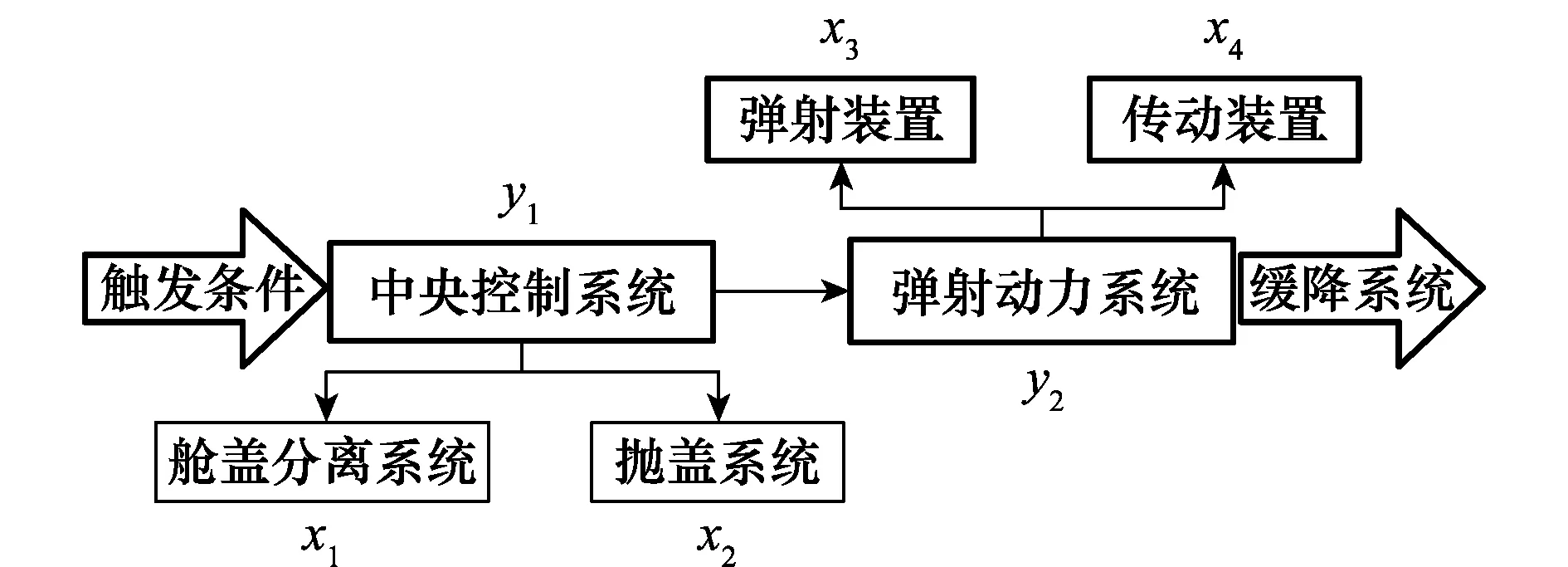
图5 可脱离应急跟踪记录设备弹射系统工作原理示意图Fig.5 Diagram of working principle of an ejection system inan emergency tracking and recording device
由于民航飞机产品在可靠性、安全性和适航性等方面的高标准要求以及民用航空飞机对于现有相对成熟的黑匣子的高度依赖,鲜有航空制造公司涉足类似产品研发,因此可供该系统可靠性分析的知识和数据并不足以满足实际的需求。因此在进行该系统可靠性分析时,部件和系统的故障状态以及故障逻辑关系等特征量含有很大程度的灰信息特征。
根据该弹射系统的工作原理可构建其可靠性分析广义灰色贝叶斯网络(见图6),其中根节点x1,x2,x3,x4分别表示抛盖动力系统、舱盖分离系统、弹射装置以及传动装置;中间节点y1和y2分别代表中央控制系统和弹射动力系统;叶节点T代表整个弹射系统。
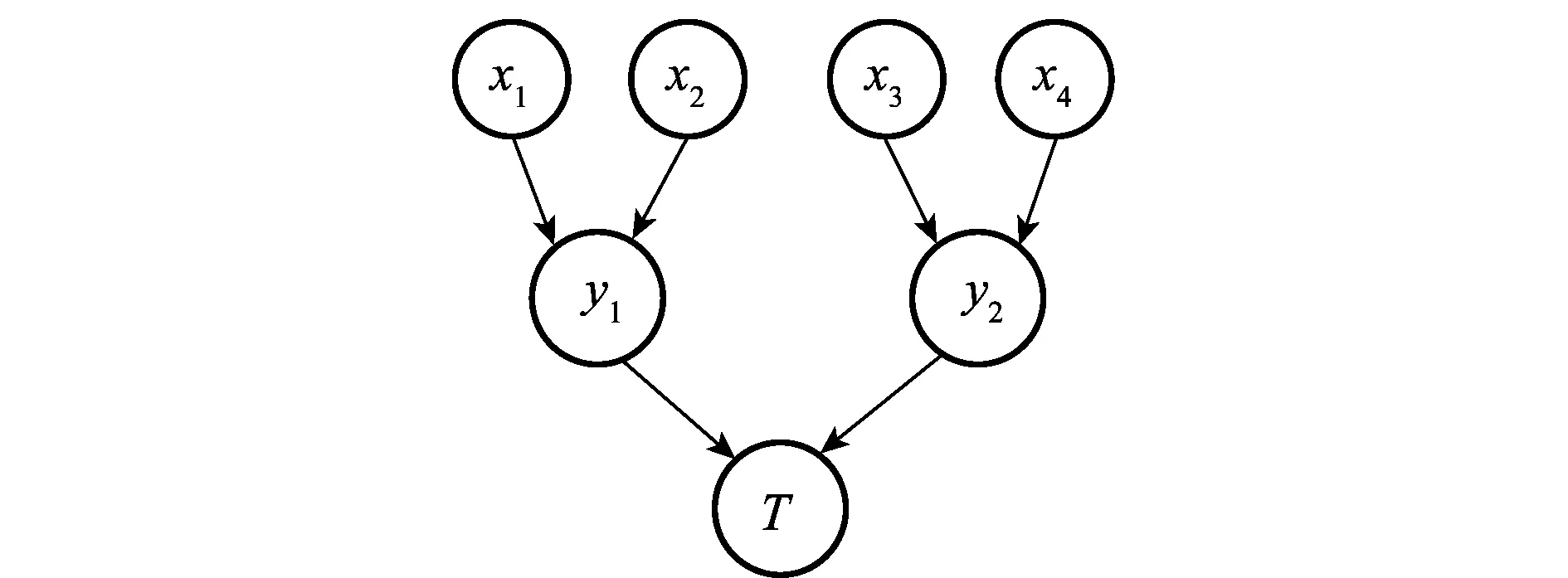
图6 某可脱离应急跟踪记录设备弹射系统可靠性分析贝叶斯网络图Fig.6 Bayesian network for reliability analysis of the ejection system in an emergency tracking and recording device
将部件和系统的故障状态集合设定为{0,0.5,1},根据现有可供参考的系统可靠性信息,可以得到各个节点性能状态的灰色模糊隶属度系和条件概率如表5~表8所示。

表5 节点y1的条件概率表

表6 节点y2的条件概率表

表7 节点T的条件概率表

表8 根节点故障状态隶属度
根据桶消元法以及式(1)可以求得
P⊗(T=0)=⊗10((203⊗5/10 000)+((33⊗7)/100)×((3⊗1/50)+(51⊗5/500)+(71/1 000))+(⊗7/100)×((33⊗1/400)+(17⊗5/200)+0.13)+⊗9((1419⊗3/40000)+(33⊗5/2000)+⊗7(((3⊗1/20)+(61/200))/100))+0.0017)+0.33⊗7((3⊗1/80)+(17⊗5/200)+⊗3((3⊗1/20)+0.305)+0.034)
根据式(6),叶节点处于故障0态的概率取值范围求解规划为
minP⊗(T=0)
最终求得叶节点处于该状态的概率取值范围为[0.031 4,0.043],同理可求得系统处于其他两种状态的取值范围如表9所示。

表9 系统叶节点处于不同故障状态的概率取值范围
根据区间灰数大小比较规则,可得P(T=1)>P(T=0)>P(T=0.5)。弹射系统出现完全故障和正常工作的概率均高于处于半故障状态的概率,且系统发生完全失效的可能性最大。
根据式(1)~式(3),可求得系统叶节点处于故障0.5态时各根节点处于不同故障状态的后验概率如表10所示。根据文献[21]可得根节点后验概率大小顺序为P(x1=0|T=0.5)>P(x4=0|T=0.5)>P(x2=0|T=0.5)>P(x3=0|T=0.5);P(x3=0.5|T=0.5)>P(x2=0.5|T=0.5)>P(x4=0.5|T=0.5)>P(x1=0.5|T=0.5)。因此,当检测到系统出现性能退化时,根据各根节点的后验概率可以对系统进行健康状态诊断。若检测正常工作的根节点则按照x1,x4,x2,x3的顺序进行检测;若检测可靠性出现退化的节点则按照x3,x2,x4,x1的顺序进行检测。叶节点处于完全故障状态下的根节点后验概率如表11所示。

表10 叶节点处于故障状态0.5下的根节点后验概率表

表11 叶节点处于完全故障状态下的根节点后验概率表
由表11可得,P(x1=0|T=1)>P(x4=0|T=1)>P(x2=0|T=1)>P(x3=0|T=1);P(x4=0.5|T=1)>P(x2=0.5|T=1)>P(x3=0.5|T=1)>P(x1=0.5|T=1)。因此当检测到系统完全故障时,若检测正常工作的节点则按照x1,x4,x2,x3的顺序;若检测可靠性轻度退化的节点应按照x4,x2,x3,x1的顺序进行检测;若检测完全故障的节点应按照x3,x2,x1,x4的顺序进行检测。节点灰色概率重要度如表12所示。

表12 节点灰色概率重要度

表13 节点状态重要度
5 结 论
(1)本文基于不确定性分析领域中的模糊数学和灰色系统理论,构建了一种广义灰色贝叶斯网络。该网络模型运用包含区间灰数的模糊集合表示部件和系统的性能状态,更有利于描述现实多态系统界限并不明显的故障状态;采用区间灰数表示系统和部件之间的条件概率,更能表现多态系统复杂多样的故障逻辑关系,同时也提高了贝叶斯网络处理多种不确定性因素的能力。
(2)提出了一种系统可靠性特征参量区间值分析方法。基于广义灰色贝叶斯网络推理算法以及灰色全局优化算法,能够推断出系统处于某些故障状态的概率以及部件重要度等可靠性特征参量的取值范围,利用区间灰数的比较法则进一步挖掘出了系统可靠性特征信息,从而为不确定条件下的多态系统可靠性分析提供了理论指导与决策支持。
(3)本文通过某民航飞机的可脱离应急跟踪记录设备弹射系统的可靠性分析实例,介绍了所提模型在多态系统可靠性分析、重要性测度等方面的应用可行性,为工程实际中的多态系统可靠性分析和故障诊断等问题提供了较为完整的解决方案。
[1] BARLOW R E, WU A S. Coherent systems with multi-state components[J].Mathematics of Operations Research,1978,3(4):275-281.
[2] ZAITSEVA E, LEVASHENKO V. Multiple-valued logic mathematical approaches for multi-state system reliability analysis[J]. Journal of Applied Logic, 2013, 11(3): 350-362.
[3] LISNIANSKI A. Application of extended universal generating function technique to dynamic reliability analysis of a multi-state system[C]∥Proc.of the International Symposium on Stochastic MODELS in Reliability Engineering, 2016: 1-10.
[4] ERYILMAZ S, BOZBULUT A R. An algorithmic approach for the dynamic reliability analysis of non-repairable multi-state weighted k-out-of-n: G system[J]. Reliability Engineering & System Safety, 2014, 131(3): 61-65.
[5] YU H, YANG J, MO H. Reliability analysis of repairable multi-state system with common bus performance sharing[J]. Reliability Engineering & System Safety, 2014, 132(132): 90-96.
[6] LEVITIN G, JIA H P, DING Y, et al. Reliability of multi-state systems with free access to repairable standby elements[J]. Reliability Engineering & System Safety, 2017, 167:192-197.
[7] PEARL J. Reasoning in intelligent systems: networks of plausible inference[J]. Computer Science Artificial Intelligence, 1988, 70(2):1022-1027.
[8] ZHANG X, KANG J, JIN T. Degradation modeling and maintenance decisions based on Bayesian belief networks[J]. IEEE Trans.on Reliability, 2014, 63(2): 620-633.
[9] GU Y K, YANG Z X. Reliability analysis of multi-state systems based on Bayesian network[C]∥Proc.of the International Conference on Quality, Reliability, Risk, Maintenance, and Safety Engineering, 2013: 332-336.
[10] WEBER P, JOUFFE L. Complex system reliability modelling with dynamic object oriented Bayesian networks (DOOBN)[J]. Reliabi-lity Engineering & System Safety, 2006, 91(2): 149-162.
[11] MARQUEZ D, NEIL M, FENTON N. Improved reliability mo-deling using Bayesian networks and dynamic discretization[J]. Reliability Engineering & System Safety,2010,95(4): 412-425.
[12] TONG Y J, TIEN I. Algorithms for Bayesian network mode-ling, inference, and reliability assessment for multistate flow networks[J]. Journal of Computing in Civil Engineering, 2017, 31(5): 04017051.
[13] 陈东宁,姚成玉.基于模糊贝叶斯网络的多态系统可靠性分析及在液压系统中的应用[J].机械工程学报,2012,48(16):175-183.
CHEN D N, YAO C Y. Reliability analysis of multi-state system based on fuzzy Bayesian networks and application in hydraulic system[J]. Chinese Journal of Mechanical Engineering, 2012, 48(16): 175-183.
[14] ZHANG R J, YANG W W, HE Q, et al. Joint probability inference algorithms of a Bayesian network and reliability analysis of electronic products[J]. International Journal of Industrial & Systems Engineering, 2016, 24(1):126.
[15] LIU Y, LIN P, LI Y F, et al. Bayesian reliability and perfor-mance assessment for multi-state systems[J]. IEEE Trans.on Reliability, 2015, 64(1): 394-409.
[16] HE Q, ZHA Y, ZHANG R, et al. Reliability analysis for multi-state system based on triangular fuzzy variety subset Bayesian networks[J]. Eksploatacja i Niezawodnosc-Maintenance and Reliability, 2017, 19(2): 152-165.
[17] LIU S F, LIN Y. Grey systems: theory and applications[M]. Berlin: Springer, 2010: 44-45.
[18] 刘思峰, 杨英杰, 吴利丰. 灰色系统理论及其应用[M]. 北京: 科学出版社, 2014.
LIU S F, YANG Y J, WU L F. Grey system theory and its application[M]. Beijing: Science Press, 2014.
[19] DECHTER R. Bucket elimination: a unifying framework for probabilistic inference[M]∥Learning in graphical models. Massachusetts: MIT Press, 1999: 61.
[20] 方志耕. 灰色博弈理论及其经济应用研究[D]. 南京: 南京航空航天大学, 2007.
FANG Z G. Grey game theory and its economic application[D]. Nanjing: Nanjing University of Aeronautics & Astronautics, 2007.
