基于发生函数的模糊多状态复杂系统可靠性通用评估方法
2018-01-15史跃东金家善徐一帆胡俊波
史跃东, 金家善, 徐一帆, 胡俊波
(1. 海军工程大学科研部, 湖北 武汉 430033; 2. 海军工程大学管理工程系, 湖北 武汉 430033)
0 引 言
工程领域的复杂系统多具备组成结构复杂、运行过程复杂、使用环境复杂等特点,且可靠性、安全性、可用性要求较高,然而鉴于其自身性能潜在的突变性、涌现性以及结构敏感性等原因,前述可靠性、安全性、可用性计算分析工作难度往往较大。为此,探索一类能够较为准确刻画复杂系统运行历程,真实映射其可靠性、安全性和可用性的通用模型和研究方法,一直备受行业研究人员关注,特别是在面临配套保障资源筹划、维修管理决策等与寿命周期成本密切相关的现实工程问题时,复杂系统的可靠性预测、评估技术,更是解决相关问题的关键所在,因此成为研究热点和难点。
早期受到传统建模理念和现实解算能力所限,有关复杂系统的可靠性研究工作,多假定系统性能仅为二元状态,即“正常工作”状态和“完全失效”状态。然而,长期的工作实践表明,仅依赖二元状态刻画评估系统工作性能,获取的研究结果多有欠理想,甚至与实际观测结果大相径庭,因此,亟待探索一类能够较为准确刻画系统真实运行状态的建模方法。自20世纪90年代起,多状态理论被引入复杂系统可靠性建模与评估研究领域,并被作为系统成本优化、维修决策的重要辅助工具[1-3]。文献[4-12]利用多状态理论开展复杂系统失效机理研究,建立了较为理想的可靠性多状态评估模型。文献[13-14]针对机械多状态系统,提出了一类离散化的可靠性解析方法。文献[15-16]基于贝叶斯网络理论,开展了多状态复杂系统的可靠性建模与评估研究。文献[17-21]针对一类极具代表性的相邻多状态k/n系统,给出了通用解算方法。文献[22-24]则进一步探讨了计及部件老化的多状态复杂系统的可靠性评估特殊性。
与二元理论相比,多状态理论改善了系统建模精度,能够更为真实地反映复杂系统工作历程,但同时也在一定程度上加大了模型解算的工作量,对于包括较多构件的大型复杂系统来说,解算工作量更是呈几何级数增加。为此,一类极具计算优势的通用发生函数解算方法,被纳入多状态复杂系统可靠性评估解算体系。其中,文献[25-30]在此方面开展了诸多工作;文献[31-33]则在此基础上,进一步探讨了半马尔可夫状态跃迁假设下的复杂系统多状态可靠性评估方法。
近年来,随着多状态复杂系统建模理论的逐步完善,解算方法和解算能力的迅速提升,相关研究成果已得以成功应用于复杂系统的可靠性优化设计、保障资源合理配置、维修活动科学决策等工程领域[34-40]。其中,文献[41-46]给出了典型多状态串并联冗余系统的可靠性优化分配方法;文献[47-53]则进一步针对多状态复杂系统构件失效后的维修策略选择问题,开展了相关深入研究。
虽然,以多状态理论和发生函数算法为核心的复杂系统建模和可靠性分析工作,已有部分研究成果,但随着现代工业技术的飞速发展,产品研制周期越来越短,寿命周期越来越长,有些复杂系统尚未经历足够时长的可靠性观测,就已投入高强度使用,因此,较难获取足量有效数据,用以精确评估其不同状态性能水平及其状态发生概率。同时,为降低计算载荷,采用的各类复杂系统建模简化方法、数值算法,也或多或少地在一定程度上降低了问题解算精度。为此,亟需进一步发展一类新技术和新理论,以弥补多状态复杂系统建模理论的现存技术短板。模糊多状态建模理论以及数值处理技术,正是为解决前述相关问题,被尝试引入复杂系统可靠性建模、分析与评估领域。目前,此方面的研究工作成果尚不多见[54-55]。
本文以经典串并混联通用系统模型为研究对象,旨在综合多态理论、模糊理论和发生函数理论的基础上,探究一类适用于复杂系统可靠性建模、分析与评估的程式化解算方法,用以解决由于多态性能观测数据有限或模型简化处理,可能导致的解算精度下降、解算结果失真等技术难题,进而为发展多状态复杂系统可靠性分析理论和解算方法提供技术借鉴。
1 模糊多状态系统
1.1 常规多状态系统
首先,引入多状态系统基本理念。不失一般性,假设任意多状态系统S,由n个不同功能元件j(j=1,2,…,n)组成,且第j个元件具有kj种状态性能,相关状态向量gj由式(1)确定
gj=[gj1,gj2,…,gjkj]
(1)
进一步,假设元件j在任意时刻t的性能状态为Gj(t),则有Gj(t)∈gj。这里,Gj(t)为随机变量,相关状态取值概率向量pj,计算式为
pj=[pj1(t),pj2(t),…,pjkj(t)]
(2)
综上,如果多状态系统S具有K种输出性能状态qi(i=1,2,…,K),则有式(3)成立。
(3)
式中,f(·)为由系统相应物理特性确定的构型函数。
1.2 模糊多状态系统
如前论述可知,多状态系统S的输出性能qi及其概率分布,可由系统组成元件j的状态向量gj、概率向量pj以及系统构型函数f(·)唯一确定。然而,鉴于观测时间、观测手段有限,获取gj、pj两类向量的精确值往往较难,而多采用区间值或模糊值代替。由此,为更加有效地基于现有观测手段、观测数据,分析获取所研多状态系统的性能分布及可靠性参数,模糊多状态理论被引入其中。后续内容,统一使用“~”上标符号,标识模糊数学量。

(4)
式中,模糊数的表达方式有多种,这里选用满足kaufumann-gupta排序规则的三角模糊数M,数学定义为
M=[a,b,c]
(5)
式中,模糊数间的排序运算,参照如下次序实施。
(6)
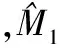
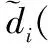

(7)

(8)


SRi={ri∈Ri|ri≥0}
(9)
由此,可将式(7)左侧表达式改写为
(10)
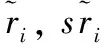
(11)
2 发生函数法
多状态建模理论,与传统的二元建模理论相比,关于系统运行历程的刻画,更为贴近真实工况,能够较为准确地反映系统运行特性。但鉴于建模状态增多,导致解算工作趋于复杂,对于引入模糊多状态建模理论的复杂系统而言,更是如此。由此,为提升复杂系统可靠性建模的程式化程度,有效释放解算资源,基于生成序列的发生函数法,被应用于可靠性分析、评估领域,并发挥重要作用。
2.1 通用发生函数
首先,给出发生函数的基本定义。不失一般性,考虑n个独立随机变量Xj,以及与其相关的随机变量Y=f(X1,X2,…,Xn),其中,变量Xj存有kj种状态,且满足概率分布
pxj=Pr{Xj=xj}
则可定义变量Xj的z变换函数为
进一步,通过引入通用发生算子Ωf,则可确定关联变量Y的z变换函数为
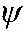
(12)
注意,若将变量Y视为系统输出,Xj视为组成元件的性能输入,f(·)视为系统构型函数,且按规则
(xj,pj)=[(xj1,pj1),…,(xjkj,pjkj)]
量化变量Xj的概率分布,则式(12)可进一步写为
(13)

2.2 模糊通用发生函数
引入模糊多状态理论,仍针对由n个元件j组成的多状态系统S,沿用式(4)中符号定义,则有元件j的模糊z变换函数uj(z)为
(14)
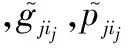
(15)

式中,sup(·)为上确界函数;min(·)为最小值函数。
3 模糊复杂系统可靠性评估建模
3.1 通用模型
工程复杂系统一般多具有元件构成多、逻辑关联结构多变等特征,就可靠性建模分析而言,存有串联、并联、串并混联、桥联等多种结构可能。鉴于串联、并联结构均为串并混联结构的一类特殊情形,桥联结构亦可利用数学手段转换为串并混联结构,考虑到模型确立的普适性,这里选用典型串并混联结构模型,作为文中模糊多状态复杂系统可靠性分析的通用模型,如图1所示。
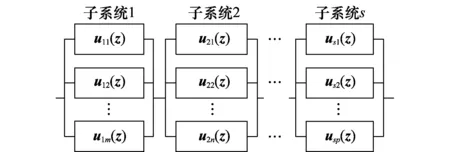
图1 典型串并混联结构Fig.1 Classic series parallel hybrid structure
图1中,变量m,n,s,p均取自然数,uij(z)为相关元件的z变换函数。
3.2 模糊多状态系统可用度评估
(16)




(17)
式中

4 典型算例
4.1 初始假设
以某型船用汽轮发电系统为例,如图2所示,由供汽、主发电、备用发电3个子单元构成。其中,供汽单元包括两台蒸汽锅炉,负责联合提供蒸汽工质;发电单元由汽轮机和发电机构成,主、辅发电单元互为备用,择一提供电力载荷。鉴于船用汽轮发电系统,组成结构复杂,海上运行环境恶劣,运行工况多样,且性能状态精确观测不易,可将其视为模糊多状态复杂系统处理,并选用三角模糊数,量化描述系统模糊状态。
进一步,假定利用期望功率输出比η,判定系统及其各级组成单元的性能状态等级。对于图2所示系统,参照文献[28]中稳态计算结果,并综合行业专家经验,有如下初始条件,见表1。

图2 船用汽轮发电系统组成框架Fig.2 Frame structure of marine boiler turbine generator system

j1(锅炉1)2(锅炉2)pj1(0.00007,0.0001,0.00012)(0.00007,0.0001,0.00012)pj2(0.0061,0.0066,0.0070)(0.0061,0.0066,0.0070)pj3(0.9927,0.9933,0.9938)(0.9927,0.9933,0.9938)gj1(0,0,0)(0,0,0)gj2(0.5,0.6,0.7)(0.5,0.6,0.7)gj3(0.9,0.9,0.9)(0.9,0.9,0.9)j3(汽轮机1)4(发电机1)pj1(0.00015,0.0002,0.00025)(0.0025,0.003,0.0034)pj2(0.0160,0.0164,0.0169)(0.9968,0.997,0.9972)pj3(0.9829,0.9834,0.9838)-gj1(0,0,0)(0,0,0)gj2(0.73,0.8,0.88)(1.0,1.0,1.0)gj3(1.0,1.0,1.0)-j5(汽轮机2)6(发电机2)pj1(0.008,0.0083,0.0088)(0.0024,0.003,0.0035)pj2(0.9910,0.9917,0.9920)(0.9965,0.997,0.9976)pj3--gj1(0,0,0)(0,0,0)gj2(0.80,0.85,0.90)(1.0,1.0,1.0)gj3--
由表1可知,汽轮发电系统中供汽锅炉运行性能存有3种状态,即完全失效状态、部分失效状态和充分工作状态,且2台供汽锅炉运行性能完全一致;类似地,主发电单元汽轮机运行性能也存有3种状态,完全失效状态、部分失效状态和完全工作状态;与主发电单元不同,辅发电单元汽轮机运行性能要求较宽松,仅存有2种状态,完全失效状态和充分工作状态;最后,主辅发电机均性能稳定,较难发生失效,仅存有完全失效和完全工作2种状态。
4.2 系统模糊发生函数
鉴于工程实际应用中,往往重点关注所研系统的稳态输出性能。因此,文中以下各类量化计算,均以此为基本前提,不再额外说明。
首先,计算船用汽轮发电系统各组成单元的模糊z变换函数Uj(z),这里以汽轮机1和发电机1组成的主发电单元U2(z)为例,解算说明如下,其他相关单元不再赘述。
(18)
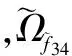
(0.002 6,0.003 2,0.003 7)z0+
(0.015 9,0.016 4,0.016 9)z(0.73,0.80,0.88)+
(0.979 8,0.980 4,0.981 0)z1
(19)
类似地,可求供汽单元和辅发电单元模糊z变换函数U1(z)、U3(z)分别为
U1(z)=10-7(0.049,0.1,0.144)z0+
10-5(0.085 4,0.132,0.168)z(0.25,0.3,0.35)+
10-3(0.139,0.198 7,0.238 5)z0.45+
10-4(0.372 1,0.435 6,0.49)z(0.5,0.6,0.7)+
(0.012 1,0.013 1,0.013 9)z(0.7,0.75,0.80)+
(0.985 5,0.986 6,0.987 6)z0.9
(20)
U3(z)=(0.010 4,0.011 3,0.012 3)z0+
(0.987 5,0.988 7,0.989 6)z(0.80,0.85,0.90)
(21)

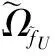
10-4(0.269 8,0.361 7,0.456 1)z0+
10-5(0.085 1,0.132,0.168 6)z(0.25,0.30,0.35)+
10-3(0.138 5,0.198 7,0.239 3)z0.45+
10-4(0.370 7,0.435 6,0.491 7)z(0.5,0.6,0.7)+
(0.012 1,0.013 1,0.013 9)z(0.7,0.75,0.8)+
10-3(0.163,0.182 8,0.205 3)z(0.73,0.8,0.88)+
(0.018,0.019 1,0.020 1)z(0.80,0.85,0.9)+

(22)
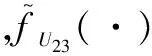
分析式(22)可知:①船用汽轮发电系统作为一类模糊多状态复杂装备系统,具有8种不同运行状态,相关状态性能及其概率分布模糊特征明显,较难实现量化精确描述,这里采用三角模糊数方法,实现模糊特征的量化描述;②若8类运行状态,按照量化性能数值,依次从小到大排序(0→1,(0.25,0.30,0.35)→2,…,0.9→8),则比照不同状态概率分布量值可知,汽轮发电系统运行处于第5、7、8类状态的几率较大,即系统常态运行功率长期保持于设计功率的70%以上;③已知汽轮发电系统各构成单元发生函数Ui(z)的前提下,全系统的多类模糊运行状态,可通过引入模糊发生算子Ω,嵌套迭代解算,运算过程仅涉及数乘、求和等简单代数运算,计算资源依赖程度低、程式化大、解算速度快。
4.3 系统可用度评估
(23)

表2 模糊集势函数计算结果
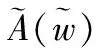

10-3(0.163,0.182 8,0.205 3)0.32+
(0.018,0.019 1,0.020 1)0.791 7+
(0.963 6,0.967 3,0.970 7)=
(0.977 9,0.982 5,0.986 7)
(24)
5 结 论
以串并混联船用汽轮发电结构为对象,开展了模糊多状态复杂系统可靠性通用评估方法研究。结合通用发生函数,给出了模糊多状态可靠性建模、分析、评估方法,并针对典型案例实施了模糊需求下多状态复杂系统的可用度解算和评估。解算与评估表明,文中建模、分析、评估方法合理,能真实反映多状态复杂系统的可靠性特征;克服观测数据不确定性的模糊数学处理方法有效,可靠性评估结论更真实可靠;回避大自由度微分运算的可靠性单元通用发生函数描述方法,解算优势明显、适用范围更广。
文中建模、解算方法,丰富、发展了复杂系统多状态可靠性评估理论,可为有关模型实体的维修决策提供理论支撑和技术借鉴。下一步拟拓展文中研究结果,结合元启发式计算技术,探讨多状态复杂系统的可靠性设计及部组件配置优化方法。
[1] ANATOLY L, ILIA F, YI D. Multi-state system reliability analysis and optimization for engineers and industrial managers[M]. London: Springer Press, 2010.
[2] KRZYSZTOF K, JOANNA S B. Reliability and safety of complex technical systems and processes[M]. London: Springer Press, 2011.
[3] GU Y K, LI J. Multi-state system reliability: a new and systematic review[J]. Procrdia Engineering, 2012, 29(4): 531-536.
[4] GREGORY L. Reliability of multi-state systems with two failure-modes[J].IEEE Trans.on Reliability,2003,52(3):340-348.
[5] JOSE E R, DAVID W C. Composite importance measures for multi-state systems with multi-state components[J]. IEEE Trans.on Reliability, 2005, 54(3): 517-529.
[6] FAN H, SUN X. A multi-state reliability evaluation model for P2P networks[J]. Reliability Engineering & System Safety, 2010, 95(4): 402-411.
[7] 周金宇, 谢里阳, 王学敏. 多状态系统共因失效分析及可靠性模型[J]. 机械工程学报, 2005, 41(6): 66-70.
ZHOU J Y, XIE L Y, WANG X M. Analysis for common cause failure and reliability model in multi-state systems[J]. Journal of Mechanical Engineering, 2005, 41(6): 66-70.
[8] 周金宇, 谢里阳. 多状态系统共因失效机理与定量分析[J]. 机械工程学报, 2008, 44(10): 77-82.
ZHOU J Y, XIE L Y. Common cause failure mechanism and risk probability quantitative estimation of multi-state systems[J]. Journal of Mechanical Engineering, 2008, 44(10): 77-82.
[9] KRISITIANSEN M, NATVIG B, WINTER R. Assessing software reliability of multistate systems[C]∥Proc.of the European Safty and Reliability Conference, 2014: 2807-2814.
[10] KOLOWROCKI K, KULIGOWSKA E. On multistate technical system operation process influence on its reliability[C]∥Proc.of the European Safty and Reliability Conference, 2015: 2099-2106.
[11] DONG R S, ZHU Y Y, XU Z B, et al. Decision diagram based symbolic algorithm for evaluating the reliability of a multistate flow network[J]. Mathematical Problems in Engineering, 2016, 45(6): 70-81.
[12] YEH W C. An improved sum of disjoint products technique for symbolic multi-state flow network reliability[J]. IEEE Trans.on Reliability, 2015, 64(4): 1185-1193.
[13] 钱文学, 尹晓伟, 谢里阳. 多状态机械系统可靠性的离散化建模方法[J]. 东北大学学报, 2008, 29(11): 1609-1612.
QIAN W X, YIN X W, XIE L Y. Discretized modeling process of reliability of multi-state mechanical systems[J]. Journal of Northeastern University, 2008, 29(11): 1609-1612.
[14] ORTEGA E M, ALONSO J, ORTEGA Q, et al. Comparisons of multistate models with discrete-time pure-birth process for recurrent events and uncertain parameters[J]. Communications in Statistics-Theory and Methods, 2016, 45(6): 1733-1746.
[15] 尹晓伟, 钱文学, 谢里阳. 基于贝叶斯网络的多状态系统可靠性建模与评估[J]. 机械工程学报, 2009, 45(2): 206-212.
YIN X W, QIAN W X, XIE L Y. Multi-state system reliability modeling and assessment based on Bayesian networks[J]. Journal of Mechanical Engineering, 2009, 45(2): 206-212.
[16] WANG J, LEE C J. Multistate Bayesian control chart over a finite horizon[J].Operations Researrch,2015,63(4): 949-964.
[17] 宋月, 刘三阳, 冯海林. 相邻k/n(F)多状态可修系统的可靠性分析[J]. 系统工程与电子技术, 2006, 28(2): 310-312.
SONG Y, LIU S Y, FENG H L. Reliability analysis of consecutivek-out-of-n:Frepairable systems with multi-state component[J]. Systems Engineering and Electronics, 2006, 28(2): 310-312.
[18] 武月琴, 周泓, 官建成. 一类多状态系统的可靠性计算[J]. 北京航空航天大学学报, 2007, 33(8): 968-971.
WU Y Q, ZHOU H, GUAN J C. Reliability estmiation of a multi-state system[J]. Journal of Beijing University of Aeronautics and Astronautics, 2007, 33(8): 968-971.
[19] TIAN Z G, RICHARD C, ZUO M J, et al. Reliability bounds for multi-statek-out-of-nsystems[J]. IEEE Trans.on Reliability, 2008, 57(1): 53-58.
[20] ERYILMAZ S. Lifetime of multistatek-out-of-nsystems[J]. Quality and Reliability Engineering Internationnal, 2014,30(7): 1015-1022.
[21] KHORSHIDI H A, GUNAWAN I, IBRAHIM M Y. On reliability evaluation of multistate weightedk-out-of-nsystem using present value[J].Engineering Economist,2015,60(1):22-39.
[22] HSIEH J, UCCI D R, KRAFT G D. Multi-state degradable system modeling and analysis[J]. Electronics Letters, 1989, 25(23): 1557-1558.
[23] LIU Y, CHEN C J. Dynamic reliability assessment for nonrepairable multistate systems by aggregating multilevel imperfect inspection data[J]. IEEE Trans.on Reliability, 2017, 66(1): 915-923.
[24] LAM Y, TSE Y K. Optimal maintenance model for a multistate deteriorating system: a geometric process approach[J]. International Journal of Systems Science,2015,34(5):303-308.
[25] LI Y F, ZIO E. A Multi-state model for the reliability assessment of a distributed generating system via universal generating function[J]. Reliability Engineering & System Safety, 2012, 106(5): 28-36.
[26] 高鹏, 谢里阳. 基于改进发生函数方法的多状态系统可靠性分析[J]. 航空学报, 2010, 31(5): 934-939.
GAO P, XIE L Y. Reliability analysis of multi-state systems based on improved universal generating function[J]. Acta Aeronautica et Astronautica Sinica, 2010, 31(5): 934-939.
[27] 李春洋, 陈循, 易晓山. 基于向量通用生成函数的多性能参数多态系统可靠性分析[J].兵工学报,2010,31(12):1604-1610.
LI C Y, CHEN X, YI X S. Reliability analysis of multi-state system with multiple performance parameters based on vector-universal generating function[J]. Acta Armamentarii, 2010, 31(12): 1604-1610.
[28] 史跃东,陈砚桥,金家善.舰船装备多状态可修复系统可靠性通用生成函数解算方法[J].系统工程与电子技术,2016,38(9):2215-2220.
SHI Y D, CHEN Y Q, JIN J S. Reliability analysis for warship armament multi-state repairable system based on universal generating function method[J]. Systems Engineering and Electronics, 2016, 38(9): 2215-2220.
[29] CAI C H, XU Y Y, KE D F, et al. Deep neural networks with multistate activation functions[J]. Computational Intelligence and Neuroscience, 2015, 73(4): 1042-1050.
[30] FRANCISCO J B, MARCELO L,RENE P T. Active current balancing technique employing the Lunze’s transformation for converters based on multistate switching cells[C]∥Proc.of the 13th IEEE Brazilian Power Electronics Conference and 1st Southern Power Electronics Conference, 2016: 99-105.
[31] OURANIA C, NIKOLAOS L, SONIA M. Multi-state reliability systems under discrete time semi-Markovian hypothesis[J]. IEEE Trans.on Reliability, 2011, 60(1): 80-87.
[32] 尚彦龙,蔡琦,赵新文,等.基于UGF和Semi-Markov方法的反应堆泵机组多状态可靠性分析[J].核动力工程,2012,33(1): 117-123.
SHANG Y L, CAI Q, ZHAO X W, et al. Multi-state reliability for pump group in nuclear power system based on UGF and semi-Markov process[J]. Nuclear Power Engineering, 2012, 33(1): 117-123.
[33] CHAMOLA V, SIKDAR B. A multistate Markov model for dimensioning solar powered cellular base stations[J]. IEEE Trans.on Sustainable Energy, 2015, 6(4): 1650-1652.
[34] BAI G H, ZUO M J, TIAN Z G. Ordering heuristics for reliability evaluation of multistate networks[J]. IEEE Trans.on Reliability, 2015, 64(3): 1015-1023.
[35] JIA X J, SHEN J Y, XING R. Reliability analysis for repairable multistate two-unit series systems when repair time can be neglected[J].IEEE Trans.on Reliability,2016,65(1):208-216.
[36] GHEISI A, NASER G. Multistate reliability of water-distribution systems: comparison of surrogate measures[J]. Journal of Water Resources Planning and Management,2015,141(10):520-529.
[37] LEVITIN G, XING L D, DAI Y S. Linear multistate consecutively-connected systems subject to a constrained number of gaps[J].Reliability Engineering and System Safety,2015, 133(133):246-252.
[38] YEH W C. A fast algorithm for quickest path reliability evaluations in multi-state flow networks[J]. IEEE Trans.on Reliability, 2015, 64(4): 1175-1184.
[39] GU Y K, CHEN J, CHENG Z X, et al. Reliability analysis of multi-state repairable system with dynamic transition probabilities[J]. Journal of Shanghai Jiaotong University (Science), 2016, 21(5): 615-620.
[40] LIN Y K, CHEN S G. A merge search approach to find minimal path vectors in multistate networks[J]. International Journal of Reliability,Quality and Safety Engineering,2017,24(1): 652-659.
[41] GREGORY L, ANATOLY L, HANOCH B H, et al. Redundancy optimization for series-parallel multi-state systems[J]. IEEE Trans.on Reliability, 1998, 47(2): 165-172.
[42] ZHAO J H, LIU Z H, DAO M T. Reliability optimization using multi-objective ant colony system approaches[J].Reliability Engineering & System Safety, 2007, 92(1): 109-120.
[43] TIAN Z G, ZUO M J. Reliability-redundancy allocation for multi-state series-parallel systems[J]. IEEE Trans.on Reliability, 2008, 57(2): 303-309.
[44] KWIATUSZEWSKA S. Multistate system reliability models with independent and dependent redundancy application in port transport[C]∥Proc.of the 25th European Safty and Reliability Conference, 2015: 1281-1286.
[45] WANG J, LI M. Redundancy allocation optimization for multistate systems with failure interactions using semi-markov process[J].Journal of Mechanical Design,2015,137(10):42-52.
[46] WANG J, LI M. Redundancy allocation for multistate systems with component dependencies and load sharing[J]. Journal of Mechanical Design,2016,138(11):142-152.
[47] LIU Y, HUANG H Z. Optimal selective maintenance strategy for multi-state systems under imperfect maintenance[J]. IEEE Trans.on Reliability, 2010, 59(2): 356-367.
[48] MUSTAPHA N, MOHAMED C F, MAHDI M. An integrated model for production and preventive maintenance planning in multi-state systems[J].IEEE Trans.on Reliability,2010,59(3): 496-506.
[49] DAO C D, ZUO M J, PANDEY M. Selective maintenance for multi-state series-parallel systems under economic dependence[J]. Reliability Engineering & System Safety,2014,121(1): 240-249.
[50] DAO C D, ZUO M J. Selactive maintenance for multistate series systems with s-dependent components[J]. IEEE Trans.on Reliability, 2016, 65(2): 525-539.
[51] WANG B, WU Z, XIA X H. A multistate-based control system approach toward optimal maintennace planning[J]. IEEE Trans.on Control Systems Technology, 2017, 25(1): 374-381.
[52] ZHOU Y F, LIN T R, SUN Y, et al. An effective approach to reducing strategy space for maintenance optimisation of multistate series-parallel systems[J].Reliability Engineering and System Safety, 2015, 138: 40-53.
[53] 余金龙, 赵文会, 赵波, 等. 基于多状态建模的独立型微网优化配置[J]. 电力系统自动化, 2015, 39(6): 11-17.
YU J L, ZHAO W H, ZHAO B, et al. Optimal configuration of standalone microgrid based on multistate modeling[J]. Automation of Electric Power Systems, 2015, 39(6): 11-17.
[54] 鄢民强, 杨波, 王展. 不完全覆盖的模糊多状态系统可靠性计算方法[J]. 西安交通大学学报, 2011, 45(10): 109-114.
YAN M Q, YANG B, WANG Z. Reliability assessment for multistate system subject to imperfect fault coverage[J]. Journal of Xi’an Jiaotong university, 2011, 45(10): 109-114.
[55] CHANG P C, LIN Y K. Reliability analysis for an apparel manufacturing system applying fuzzy multistate network[J]. Computers and Industrial Engineering,2015,88(2):458-469.
