基于聚类的新型多目标分布估计算法及其应用

张秀杰, 高肖霞, 张 虎, 赵 杰

(1. 哈尔滨工业大学机电工程学院, 黑龙江 哈尔滨 150001; 2. 哈尔滨工业大学航天学院, 黑龙江 哈尔滨 150001)

0 引 言

实际工程中存在着大量的具有多约束、多变量以及非线性等性质的复杂多目标优化问题(multi-objective optimization problem, MOP)。由于大多数情况下MOP中各子目标之间相互冲突,不存在一个最优解使所有子目标同时达到最优。因此,不同于单目标优化问题只有一个或者若干个孤立的最优解,MOP具有大量的对于所有目标都可以接受的折衷解,即Pareto最优解。所有Pareto最优解组成的集合称为Pareto解集(pareto set, PS),Pareto解集投影到目标空间获得的目标向量的集合称为Pareto前沿(Pareto front, PF)。并且连续MOP的PS和PF的结构具有规则特性,即根据Karush-Kuhn-Tucker条件,在宽松的条件下,具有m个目标的连续MOP的PS(或PF)的结构是一个m-1维的分段连续的流形。对于一个MOP,由于不可能求解出其所有的Pareto最优解,因此在求解过程中,决策者往往希望获得一个有限数目的逼近解的集合(逼近解集),其对应的目标向量(构成逼近前沿)越靠近PF越好(收敛性),并且沿着PF分布越广泛以及越均匀越好(多样性)。

由于传统的确定性优化技术不能较好地对复杂的MOP进行求解,因此基于自然启发搜索的全局优化算法——演化算法(evolutionary algorithm, EA)成为了解决MOP流行的方法。多目标演化算法(multi-objective evolutionary algorithm, MOEA)具有良好的并行性、鲁棒性,而且其求解不依赖于问题特性、通用性强,并且单次运行就可获得MOP的Pareto解集的逼近,近年来得到了蓬勃发展[1]。

在EA当中,包含有个体重组和环境选择两个重要组成部分。个体重组用于产生新解,而环境选择则负责为下一代挑选有效的新解。在MOEA中,根据新解产生的方式,重组算子可以粗略地划分为两大类,即基于遗传的重组算子和基于模型的重组算子。基于遗传的MOEA应用传统的重组算子(例如:模拟二进制交叉[2]、多项式变异[3]等)产生新解。基于模型的MOEA采用概率模型描述群体中个体的分布,并通过建立的模型采样产生新个体,多元高斯模型、Bayesian网络、流形学习、密度估计等常用的机器学习方法被广泛应用于群体建模[4]。目前已有的MOEA大多数采用的是基于遗传的新解产生方法,但是基于模型的MOEA也得到了学者们越来越多的关注,近些年变得流行的多目标分布估计算法(multi-objective estimation of distribution algorithm, MEDA)就是一个重要的代表[5]。

分布估计算法(estimation of distribution algorithm,EDA)[6]是EA中一类特别的方法。EDA并不采用传统的交叉变异等遗传操作,取而代之,它从所挑选的有效解中明确地提取全局统计信息,基于提取的统计信息建立一个有效解后验概率分布模型,进而从建立的模型中抽样产生新解。在基于遗传的MOEA中,遗传操作可能会破坏种群强模式的建立,因此种群个体朝向最优解的移动方向非常难以预测。然而,MEDA能够预测PF的位置或模式,或者预测在搜索空间中有效的搜索方向。通过调整搜索使其沿着发掘或预测的有效的搜索方向,就能够较好地产生有效解。学者们已经提出了各种MEDAs,并且这些算法显示出了良好的性能。

虽然MEDA已经得到了越来越多学者的关注和研究,但是依然存在着不足,典型的有:算法中没有充分考虑MOP的规则特性,种群中的异常解处理不正确,种群多样性容易丢失,以及过多的计算开销用于构建最优的种群模型[4,7]。针对上述不足,本文提出一种基于聚类的新型多目标分布估计算法(clustering based MEDA, CEDA)。在CEDA中的每一代,首先利用聚类算法发掘种群中个体的分布结构,然后基于结构信息,为每一个个体构建一个多元高斯模型(multivariate Gaussian model, MGM),基于此模型,抽样产生新解。

1 多目标分布估计算法

EDA已经被大量地应用于MOP的求解。文献[8]提出了一种基于混合的多目标迭代密度估计演化算法(multi-objective mixture-based iterated density estimation evolutionary algorithm, MIEDA),用于求解连续和离散优化问题,MIEDA被认为是其他MEDAs的基准算法。文献[9]采用基于支配的框架并且使用K-means聚类算法进行建模,设计了一种多目标分层Bayesian优化算法(multi-objective hierarchical Bayesian optimization algorithm, mohBOA)。文献[10]提出了一种延伸的紧凑遗传算法(extended compact genetic algorithm, ECGA)以解决可扩展的欺骗问题。文献[11]将EDA集成到基于分解的MOEA框架中,提出了一种混合局部搜索元启发式方法的基于分解的EDA。文献[12]构建基于高斯过程的逆模型(inverse models)将所有已发掘的非支配解从目标空间映射到决策空间,通过对目标空间抽样产生新解,提出了基于逆模型的MOEA(inverse models multi-objective evolutionary algorithm,IM-MOEA)。

为了利用连续MOP的规则特性提高MEDA的求解性能,学者们又提出了多种基于规则特性的MEDA。文献[7]提出了一种基于规则模型的MEDA,即(regularity model-based multi-objective estimation of distribution algorithm, RM-MEDA),其使用局部主成分分析方法对有效解建立概率分布模型,并通过概率模型抽样产生新个体。在此之后,又设计了一种基于概率模型的MOEA[13],在决策空间和目标空间同时建立概率模型逼近PS和PF。受到RM-MEDA思想的启发,出现了一系列变种的RM-MEDA,例如,基于冗余类消减的MEDA[14],带有局部学习策略的MEDA[15],基于流形学习的演化多目标优化算法等[16]。

目前为止,在已有的MEDAs中,大多数在设计过程中并没有充分地考虑MOP的规则特性,并且建模过程中,只是运用较少个数的高斯模型描述有效解的分布,往往丢弃了异常解。实际上,运用较少个数的高斯模型抽样产生新解,新解大量的集中在模型的中心位置(均值)附近,多样性不足,并且异常解可能代表着新的有效区域,需要开展搜索。另外,在已有的基于规则特性的MEDAs中,大部分借鉴RM-MEDA的思想,而RM-MEDA建模复杂,在搜索的早期阶段种群的多样性保持不好,并且难以设定主成分的个数。为了改善前述问题,本文充分考虑MOP的规则特性,计划基于聚类运用较多数目的简单的高斯模型逼近种群结构,进而抽样产生新解,从而降低算法结构的复杂性,增强算法的易用性,并提高算法产生多样解的能力。

2 基于聚类的新型多目标分布估计算法

2.1 算法框架

CEDA采用凝聚层次聚类(agglomerative hierarchical clustering, AHC)算法[17]发掘种群结构,CEDA的基本框架如算法1所示。

算法1CEDA基本框架

步骤1初始化种群P={x1,x2,…,xN}和控制概率β,设置演化代数t=0。

步骤2主循环。

步骤2.1设置一个空的外部文档A=∅。

步骤2.2对种群进行聚类,

{LC1,…,LCk}=AHC(P,K)

步骤2.3构建一个全局类GC。

步骤2.4分别计算局部类LCk和全局类GC的协方差矩阵Σk(k=1,…,K)和ΣGC。

步骤2.5新解产生:对于每一个个体xi∈P,i=1,2,…,N。

步骤2.5.1为个体xi选择一个协方差矩阵Σi。

步骤2.5.2产生新个体yi=SolGen(Σi,xi)。

步骤2.5.3保留新解A=A∪{yi}。

步骤2.6环境选择:更新种群P=EnvSel(A∪P)。

步骤2.7令t=t+1。

步骤2.8如果t>T,算法结束,输出P;否则转向步骤2。

步骤3停机:输出P。

在算法1中,N代表种群大小,K为AHC中定义的最大聚类个数,T为最大演化代数,GC和LCk分别代表全局类和第K个局部类,Σki为xi所在的局部类的协方差矩阵,β表示利用LCk建立抽样池的概率(称之为重组控制概率),rand()生成一个在[0,1]区间内均匀分布的随机数。

在CEDA算法的每一代中,首先利用AHC将种群划分为K个局部类(步骤2.2),并从每一个局部类中随机抽取一个个体共同构建一个全局类(步骤2.3)。然后计算出全局类和所有局部类的协方差矩阵ΣGC和Σk(k=1,2,…,K)(步骤2.4)。紧接着为每个个体xi确定一个协方差矩阵Σi,该协方差矩阵分别以β和1-β的概率设置为Σk或ΣGC(步骤2.5.1),并且由xi和Σi构成高斯模型抽样产生新个体yi(步骤2.5.2),将yi存于外部档案A中(步骤2.5.3)。最后基于A和P利用环境选择机制更新种群P(步骤2.6)。以下小节对CEDA的细节进行详细介绍。

2.2 凝聚层次聚类算法

利用AHC算法将种群P中包含的N个个体,即P={x1,x2,…,xN},划分到K个类中的原理如算法2所示。

算法2AHC(P,K)

步骤1将种群P中每个个体看作一个类。

步骤2循环。

步骤2.1计算每两个不同的类之间的欧氏距离;

步骤2.2找出距离最小的两个类合并成新的类;

步骤2.3判断是否满足终止条件(聚类个数是否大于K),满足则终止,输出最终的聚类结果,否则转至步骤2.1。

AHC首先将每一个个体视为一个类,然后利用一系列机制合并不同类,直至种群聚类个数不大于K。在CEDA的AHC算法中利用组间平均联接算法(group average linkage algorithm)定义两个类之间的距离。关于AHC算法的细节内容参考文献[17]。

2.3 新解产生

算法1中步骤2.5.2产生新个体,此过程包含基于多元高斯模型的抽样和多项式变异,其细节如算法3所示。

算法3SolGen(Σi,xi)

步骤1利用平方根法分解协方差矩阵Σi得到一个下三角矩阵Λ,并且Σi=ΛΛT。

步骤2产生向量v=(v1,v2,…,vn)T,其中vj～N(0,I),j=1,2,…,n服从高斯分布。

步骤4修复该试验解

步骤5对试验解进行变异

y‴

aj和bj代表第j个变量的上下边界;pm为变异概率,ηm为变异指数,r=rand()。

对于种群中的每个个体,首先基于协方差矩阵为其建立多元高斯模型并抽样产生一个初始试验解(第1～3行)。然后对试验解进行修补,保证其可行性(第4行),紧接着对试验解进行变异操作以增强解的多样性(第5行),最后再次对试验解进行边界修补确保其可行(第6行)。

2.4 环境选择

每一代当新解产生完毕之后,运用EnvSel(A∪P)从A∪P中选出优秀个体进入下一代演化过程。CEDA采用(S-metric selection based evolutionary multi-objective optimization algorithm, SMS-EMOA)[18]中提出的基于超体积指标的环境选择方法。超体积指标是已知的唯一一个为“Pareto兼容(Pareto compliant)”的一元指标[19],基于超体积指标的环境选择方法在求解具有复杂PF的MOP时展现出了良好的性能[20]。EnvSel(A∪P)的具体过程如算法4所示。

算法4EnvSel(A∪P)

步骤1利用快速非支配排序方法对A∪P中的个体进行排序

{B1,B2,…,BL}=Fast_Nondominated_Sort(A∪P)

步骤2复制较优的个体到辅助种群P′中

步骤3如果l>1

循环:当|P′|>N

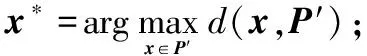
步骤3.2将x*从P′中移除,P′=P′{x*}。

步骤4如果l=1

循环:当|P′|>N

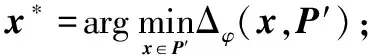
步骤4.2将x*从P′中移除,P′=P′{x*}。

步骤5将P′赋给P,P=P′。

步骤6输出P。

首先将当前种群P和外部文档A合并成一个新的种群,并且利用(nondominated sorting genetic algorithm Ⅱ, NSGA-Ⅱ)[21]中提出的快速非支配排序方法将新种群中的个体划分到L个不同的非支配前沿{B1,B2,…,BL}当中。然后根据排序的结果,将新种群中的较优个体复制到一个辅助种群P′当中,直到|P′|≥N。如果P′当中包含有多个非支配前沿(即l>1),则逐个移除第l前沿中d(x,P′)最大的个体,直到|P′|=N,d(x,P′)指的是在P′中支配x的点的个数;否则如果l=1,逐个移除P′中超体积贡献度Δφ(x,P′)最小的个体,直到|P′|=N,超体积贡献度Δφ的计算方法参考文献[18]。最后,将P′赋给P,作为下一代的种群。

2.5 算法说明

关于CEDA,有如下说明:

(1) 文献[22]指出在MOEA中,相似个体重组,能提高产生新解的质量。产生此效果的原因是增强了算法的局部搜索,暗含地利用了MOP的规则特性。与此类似,本文的CEDA采用邻近个体为每个当前个体构建高斯模型逼近种群结构进而抽样产生新解,这一机制同样增强了算法的局部搜索,充分地考虑了MOP的规则特性,理应也能更好地产生高质量的新解。

(2) 与RM-MEDA中利用局部主成分分析方法提取流形结构,然后抽样产生新解的方式相比,CEDA中的基于聚类建立高斯模型抽样产生新解的方式更简单易用。并且,在进化的早期阶段,PS的流形结构尚未显现,种群需要良好多样性,但是RM-MEDA的新解产生方式限制了新解的产生方向,不利于产生多样化的解,而CEDA利用完全协方差矩阵抽样产生新解,能从各个方向生成新解,更好地维护新解的多样性。

(3) MIEDA[8]等传统的为每一个类构建一个高斯模型进行抽样的方式,其产生的新解大量地分布在均值向量附近,新解的多样性不够,而CEDA为每个种群个体以自身为均值建立一个高斯模型抽样产生新解,实际上是为每个个体添加一个高斯扰动,此种方式能产生更为多样化的解。

(4) 在为个体构建高斯模型的时候,如果对于每个个体都计算协方差矩阵,则需要大量的建模计算开销。为了解决此问题,CEDA中使同一类中的个体共享相同的协方差矩阵进行建模从而大大降低建模计算开销。之所以能够进行此策略是因为相似的个体理应具有相近的高斯模型,并且近似的高斯模型就已经满足算法的要求,没有必要花费大量的计算开销建立精确的模型。

(5) 不同于以往丢弃异常解的建模方式,CEDA中为每个个体建立一个高斯模型进行抽样,实际上就是充分地考虑了异常解代表的解空间区域,因此能更好地加强对解空间的搜索。

3 实验分析

3.1 标准测试实例和性能度量指标

为了测试CEDA的性能,首先利用标准测试题对其进行测试。大多数工程中的MOP具有复杂的PF结构,因此CEDA算法理应适用于求解此类具有复杂PF结构的MOPs。本文利用具有复杂PF和PS结构的6道标准测试题GLT1～GLT6对CEDA进行测试。其中,GLT1～GLT4为双目标测试问题,GLT5～GLT6为三目标测试问题。(Gu F, Liu H, Tan K, GLT)测试题的具体细节参考文献[20]。

为了评估算法的性能,运用两个常用的性能指标,即反世代距离(inverted generational distance, IGD)[7,23]和超体积(hypervolume, HV)[24]度量算法获得的逼近前沿的效果。IGD和HV是两个均能够综合评价获得的逼近前沿的收敛性与多样性的性能指标。并且IGD值越小，HV值越大，代表算法所求得的逼近前沿的收敛性和多样性越好。

在接下来的实验中,计算HV指标值时,各测试题的参考点取值为:GLT1取r=(2,2)T,GLT2取r=(2,11)T,GLT3取r=(2,2)T,GLT4取r=(2,3)T,GLT5-GLT6取r=(2,2,2)T。

3.2 对比算法及参数设置

选取4种典型的MOEAs,即NSGA-Ⅱ[21]、SMS-EMOA[18]、RM-MEDA[7]和(transform each individual objective function into the one multi-objective evolutionary algorithm based on decomposition, TMOEA/D)[25],与CEDA开展对比实验。NSGA-Ⅱ是一种基于支配的MOEA,SMS-EMOA是一种基于指标的MOEA,TMOEA/D是一种用于解决具有复杂PF形状的MOPs的基于分解的MOEA,RM-MEDA是一种基于规则特性的MEDA,这几种算法涵盖了当前主流的MOEA类型。为了保证对比的公平性,所有对比算法的参数均通过前期的实验进行了系统地优化,对比实验中采用最佳的参数组合。所有算法均由Matlab进行实现,并且在同一台计算机上运行,具体的算法参数设置如下:

(1) 公共参数

(2) NSGA-Ⅱ参数

模拟二进制交叉参数Pc=0.9,ηc=20;多项式变异算子控制参数pm=1/n,ηm=20。

(3) SMS-EMOA参数

模拟二进制交叉参数Pc=0.9,ηc=20;多项式变异算子控制参数pm=1/n,ηm=20。

(4) RM-MEDA参数

聚类个数(principal component analysis, PCA)=5;局部主成分分析最大迭代次数为50;扩展采样率为0.25。

(5) TMOEA/D参数

邻居大小NS=30;第一搜索阶段演化代数T1=T/10;第二搜索阶段演化代数T2=αT,α={0.01,0.02,…,0.1,0.1,0.1,0.15};差分演化交叉算子控制参数F=0.5,CR=1。

(6) CEDA参数

重组控制概率β=0.9;最大聚类数目K=5;多项式变异算子控制参数pm=1/n,ηm=20。

为了在实验中获得统计置信的结论,每种算法对每道测试题独立运行33次,基于统计指标值(均值和标准差)进行算法性能的比较。在比较表格中,关于某一道测试题,各算法对其统计运算获得的指标值的均值进行升序(IGD指标)或降序(HV指标)排序,排序结果在表格的方括号中显示,并且每种算法对GLT测试集的计算性能排序的平均值(平均秩)也列在表格中。对于每道测试题,各算法获得的平均指标值中最优值用深灰色背景表示,次优值用浅灰色背景表示。另外,当CEDA与任一算法进行比较的时候,执行在5%显著性水平的Wilcoxon秩和检验观测差异的显著性。“†”,“§”和“≈”表示CEDA求解某问题的性能在5%显著水平上是优于、劣于以及相似于比较算法对于该问题的求解能力。

3.3 实验结果

3.3.1 质量指标

表1给出了NSGA-Ⅱ、SMS-EMOA、RM-MEDA、TMOEA/D以及CEDA算法分别独立计算GLT测试集33次各自获得的逼近前沿的HV和IGD值的统计结果。

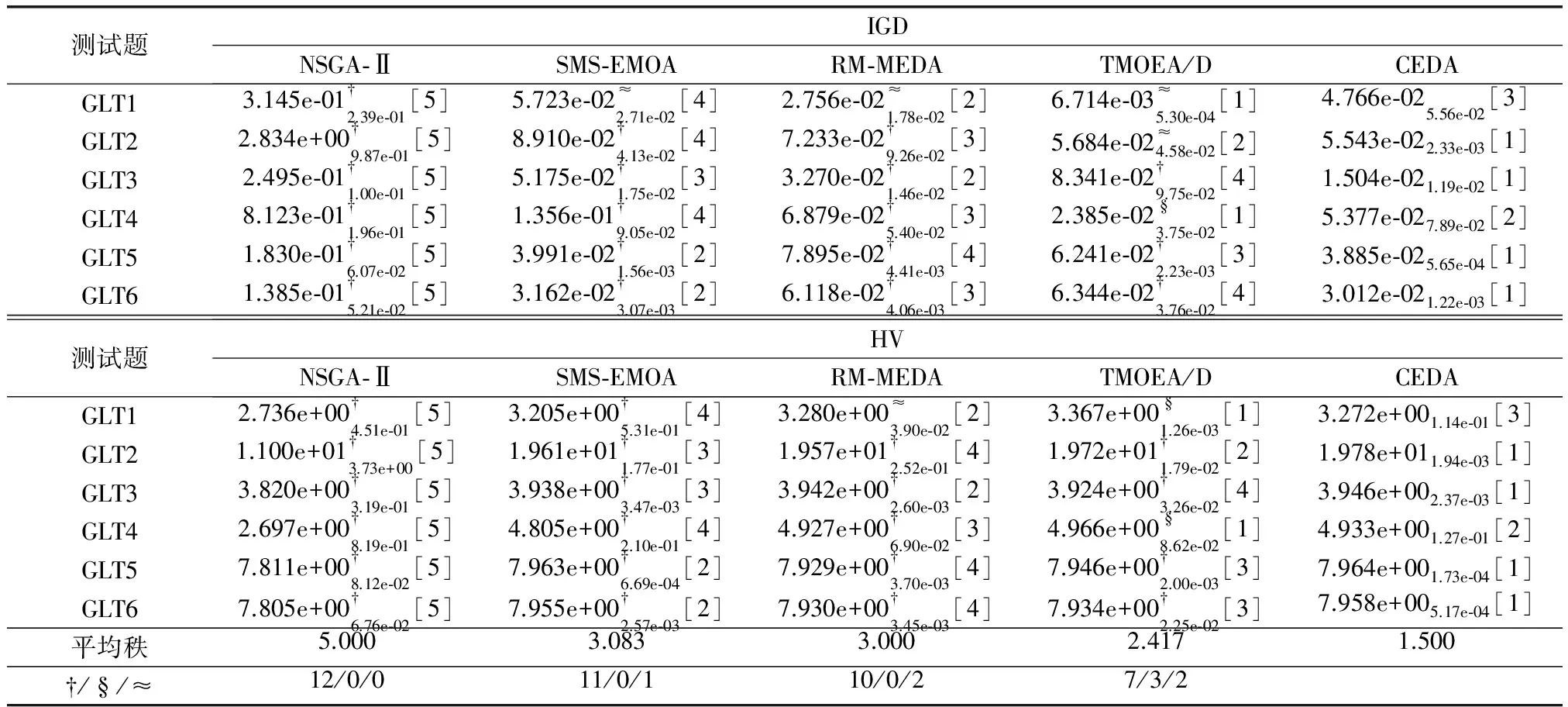
表1 NSGA-Ⅱ、SMS-EMOA、RM-MEDA、TMOEA/D以及CEDA分别独立计算GLT测试集33次所得的逼近前沿的IGD和HV指标值的统计结果(均值(标准差)[排序])

从表1中可以看出,通过演化300代,与对比算法进行比较,在12个指标值中,CEDA获得了8个最优和2个次优平均指标值。根据统计显著性检验,相对于NSGA-Ⅱ、SMS-EMOA、RM-MEDA和TMOEA/D,在与每种算法的12次比较中,CEDA分别获得了12、11、10和7个明显较优的平均指标值。另外,平均秩的值表明在求解GLT测试集时,性能从最优到最劣的算法分别是CEDA、TMOEA/D、RM-MEDA、SMS-EMOA、NSGA-Ⅱ。

3.3.2 搜索效率

图1绘制出了NSGA-Ⅱ、SMS-EMOA、RM-MEDA、TMOEA/D以及CEDA算法分别独立计算GLT测试集33次各自获得的平均IGD指标值的演化曲线。从图中可以看出对于GLT2-GLT3和GLT5-GLT6的求解中,CEDA均在最少的演化代数内获得了最低的平均IGD指标值。对于GLT1,CEDA的求解性能劣于RM-MEDA和TMOEA/D。对于GLT4,CEDA劣于TMOEA/D获得了次优的求解效果。总体而言,与其他4种相比,CEDA在求解GLT测试集的演化过程中收敛速度最快并且能够维持最好的种群多样性。

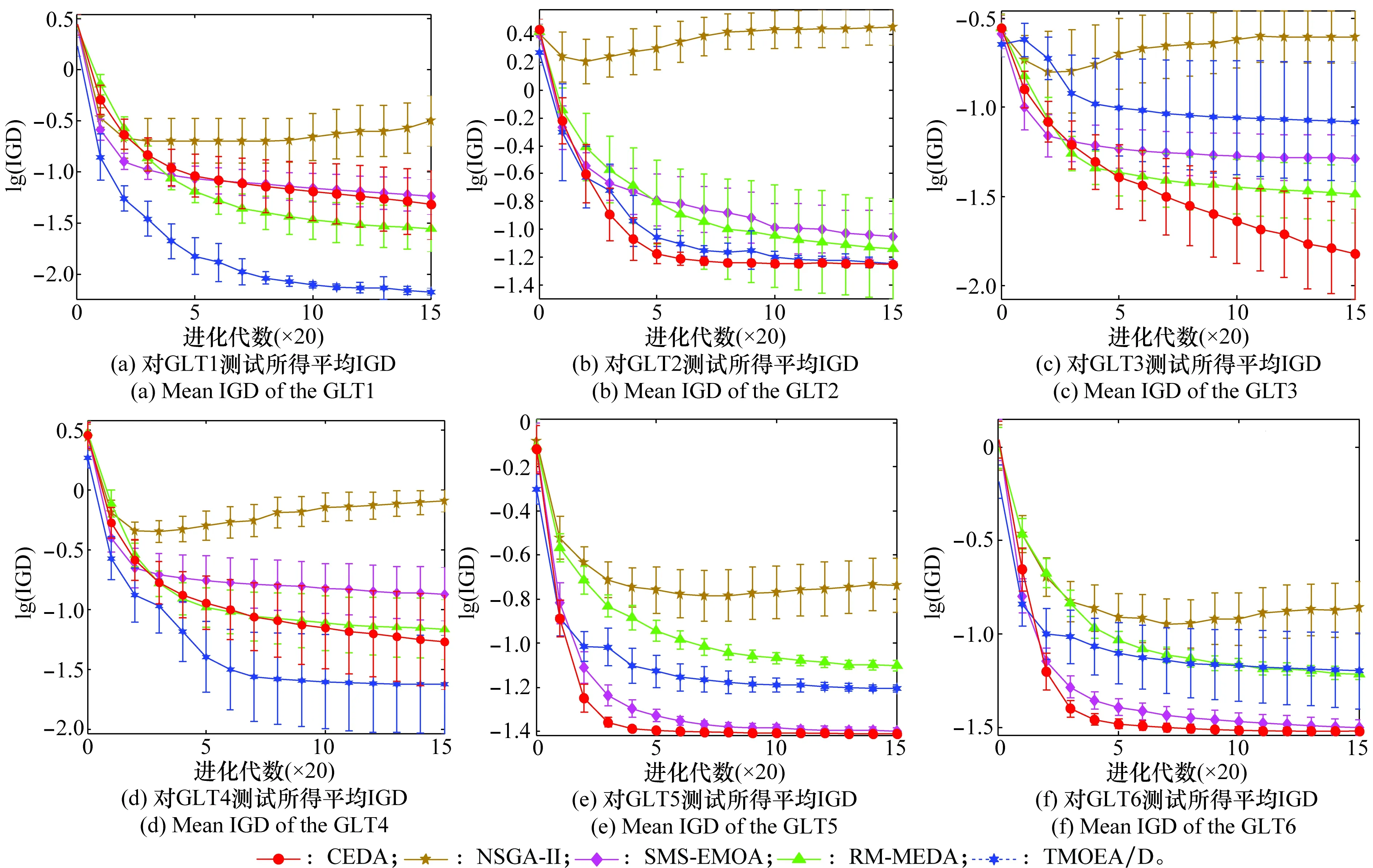
图1 平均IGD指标值演化曲线Fig.1 Evolution of the mean IGD metric values

3.3.3 结果可视化

图2绘制出了统计比较中性能最好的两种算法CEDA和TMOEA/D分别独立计算GLT测试集33次各自获得的全部最终逼近前沿(如图2(a)和2(b)),以及分别获得中位IGD指标值时对应的代表性逼近前沿(如图2(c)和2(d))。从图2(a)和2(b)可以看出,在33次独立运算中,在求解GLT1和GLT4时,CEDA获得的逼近前沿还有部分并未收敛到PFs上,但是在求解GLT2、GLT3、GLT5、GLT6时,CEDA获得的全部逼近前沿都能稳定的收敛到PFs上,而且覆盖整个PFs。然而,TMOEA/D求解GLT4获得的逼近前沿并没有全部收敛到PF上,并且求解GLT5和GLT6时,其获得的逼近前沿并未完全覆盖整个的PFs。从图2(c)和2(d)可以观察到,TMOEA/D求解GLT3和GLT4时,获得的代表性的前沿虽然最终都能收敛到PFs,但并不能完全覆盖PFs,求解GLT5和GLT6时,得到的代表性前沿中仍存在一些个体没有完全收敛到PFs,且前沿分布的均匀性也并不理想。与TMOEA/D相比,CEDA对于GLT2～GLT6获得的代表性的前沿均具有更好的收敛性和多样性。

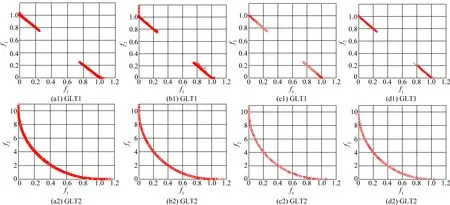
图2 TMOEA/D和CEDA获得的逼近前沿Fig.2 Approximated fronts obtained by TMOEA/D and CEDA

根据上述的质量指标、搜索效率以及结果可视化,可以推断出相对于NSGA-Ⅱ、SMS-EMOA、RM-MEDA和TMOEA/D,CEDA算法对于GLT测试集具有最佳的求解性能。

3.4 参数灵敏度分析

3.4.1 交配限制概率

在CEDA中,采用重组控制概率β维护算法演化过程中勘探与开发之间的平衡。为了分析β对算法性能的影响,采用不同β值(β=0.5,0.6,0.7,0.8,0.9)构造CEDA算法对GLT测试集进行求解,算法的其他参数与第3.2节设置相同。每种带有不同β值的算法对每道测试题进行22次独立运算,获得的逼近前沿的IGD指标值的均值和标准差如图3所示。

图3 重组控制概率(β)分析Fig.3 Mating limit probability (β) analysis

由图3可以看出,当求解GLT1,GLT3和GLT4时,不同的β值获得的平均IGD值有明显的差异,然而对其他测试题求解时,不同的β值却得到了相似的平均IGD值。但是总体来说,当β=0.9时,CEDA对于GLT1-GLT3以及GLT5-GLT6均具有较好的求解效果,因此说明算法的性能对于β的取值并不十分敏感。

3.4.2 聚类数目

CEDA中采用AHC方法发掘种群结构。为了分析AHC中的最大聚类数目K对CEDA性能的影响,采用不同K值(K=4,5,7,10,20)构造CEDA算法对GLT测试集进行求解,算法中的其他参数与第3.2节设置相同。每种带有不同K值的算法对每道测试题进行22次独立运算,获得的逼近前沿的IGD指标值的均值和标准差如图4所示。

图4 聚类数目(K)分析Fig.4 Number of cluster (K) analysis

由图4可以看出,当求解GLT1～GLT4时,不同K值的CEDA获得的平均IGD值有显著的差异,然而对于GLT5～GLT6求解时,不同的K值却得到了相近的平均IGD值。总体来说,当K=5,CEDA对于不同的测试题均能获得较小的平均IGD值,因此说明CEDA的性能对于最大聚类数目的取值也并不十分敏感。

4 工程应用

4.1 优化模型

齿轮减速器是原动机和工作机之间独立的闭式传动装置,用来降低转速和增大转矩,以满足工作需要。其无须联轴器和适配器,结构紧凑。负载分布在行星齿轮上,因而承载能力比一般斜齿轮减速机高,满足小空间高扭矩输出的需要,广泛应用于大型矿山、钢铁、化工、港口、环保等领域。虽然齿轮减速器应用广泛,但长期以来减速器的设计仅由设计人员依靠相关的资料、文献,以及多年的经验完成,因而不仅效率低,而且可能造成人力、物力和财力的浪费,因此目前需要找到一种快速有效的方法来优化设计齿轮减速器。齿轮减速器的优化设计实际上是一个多目标、多约束、多耦合的优化问题,普通的算法难以较好地求解此问题。本文以此问题为实例检验CEDA求解复杂工程优化问题的效果。文献[26-27]中建立了某轻型飞机的齿轮减速器简易模型如图5所示。

该MOP的设计目标是使减速器的体积和轴2所承受的应力最小,并且满足轮齿的弯曲应力、接触应力、轴的扭转变形以及应力等约束。该问题的数学模型描述为

图5 齿轮减速器结构简图Fig.5 Gear Reducer structure diagram

(1)

(2)

式中,x1为齿宽;x2为齿轮模数;x3为小齿轮齿数;x4为轴承1之间的距离;x5为轴承2之间的距离;x6为轴1的直径;x7为轴2的直径;g1为齿的弯曲应力约束;g2为齿的接触应力约束;g3、g4为轴的变形约束;g5、g6、g7为基于空间尺寸限制和经验约束;g8、g9为由经验得到的设计轴的要求;g10、g11为轴的应力约束;g12至g25为7个变量的上下边界。

4.2 实验设计与结果分析

利用NSGA-Ⅱ、SMS-EMOA、RM-MEDA、TMOEA/D以及CEDA对齿轮减速器优化设计模型进行求解。经过参数优化,运算过程中的参数设置如表2所示,其余设计与第3.2节相同。每种算法对模型独立运算33遍,利用超体积HV指标值度量每一次获得的逼近前沿的效果。其中,计算HV值时取参考点r=[6 600,1 600]T。

5种算法对齿轮减速器优化设计模型独立运行33次获得的HV指标值的箱型图对比结果如图6所示(图6(a)为原图,图6(b)为局部放大图)。从图6中可以看出CEDA获得了最大的中位HV指标值和最小的四分位距,从而说明CEDA对于齿轮减速器优化设计模型能稳定地求解出具有良好多样性和收敛性的解。

表2 NSGA-Ⅱ、SMS-EMOA、RM-MEDA、TMOEA/D及CEDA算法 求解齿轮减速器优化设计模型时参数设置

图7(图7(a)为原图,图7(b)为局部放大图)绘制出了NSGA-Ⅱ、SMS-EMOA、RM-MEDA、TMOEA/D以及CEDA算法分别独立计算齿轮减速器优化设计模型33次各自获得的平均HV指标值的演化曲线。从图7中可以看出CEDA在最小的演化代数内获得了最高的平均HV指标值。也就是说与其他4种相比,CEDA在演化过程中收敛速度最快并且能够维持最好的种群多样性。

图8为分别利用NSGA-Ⅱ和CEDA对齿轮减速器优化设计模型求解时,独立运算33次各自获得的全部逼近前沿以及中位IGD指标值对应的代表性逼近前沿。从图8(a)和图8(c)可以看出,CEDA获得的全部逼近前沿均能够稳定地收敛,并且与NSGA-Ⅱ获得的逼近前沿相比,其覆盖面更广。从图8(b)和图8(d)可以看出,相对于NSGA-Ⅱ,CEDA获得了更为宽广和均匀的代表性的逼近前沿。

从图6～图8的分析中可以推断出CEDA算法对于齿轮减速器优化设计模型具有优异的求解性能。

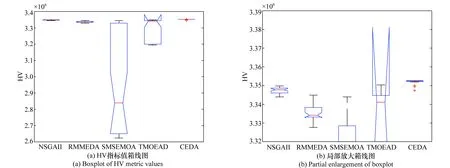
图6 NSGA-Ⅱ、SMS-EMOA、RM-MEDA、TMOEA/D以及CEDA算法对齿轮减速器优化设计模型分别独立运算33次获得的HV指标值的箱线图 Fig.6 Boxplot of HV metric values obtained by NSGA-П、SMS-EMOA、RM-MEDA、TMOEA/D and CEDA, respectively,over 33 independent runs on the application model

图7 平均HV指标值演化曲线Fig.7 Evolution of the mean HV metric values

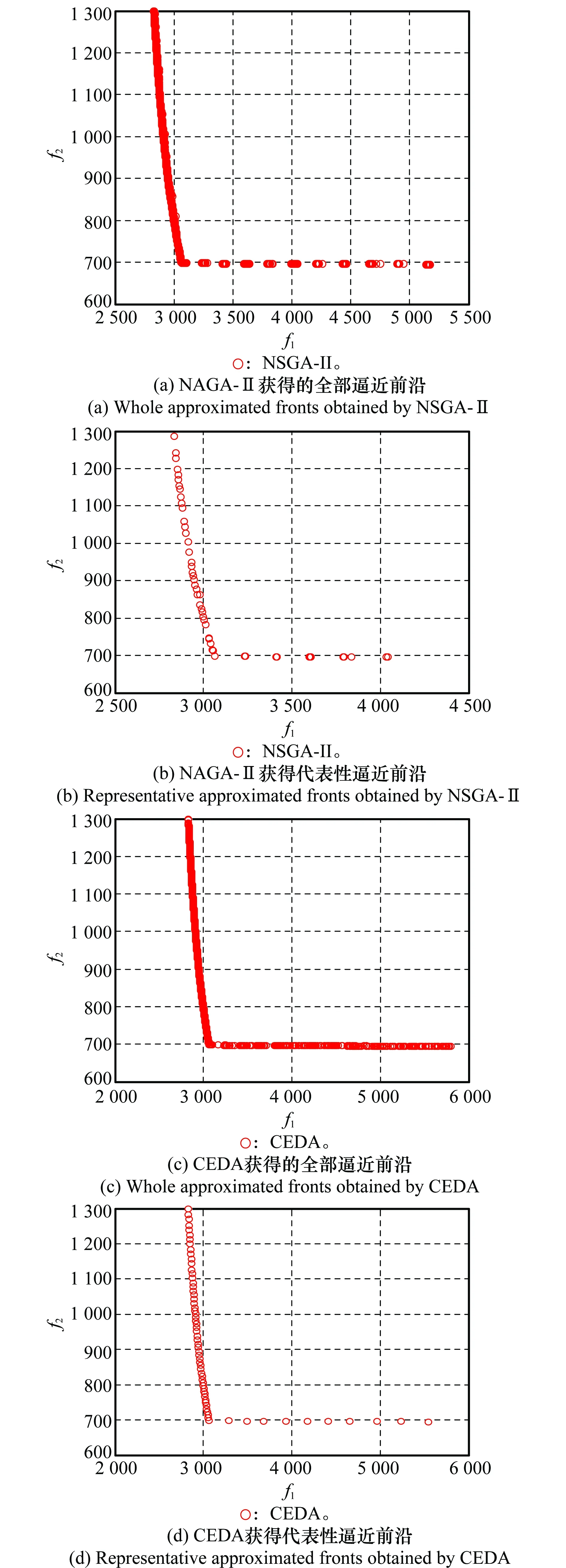
图8 NSGA-Ⅱ和CEDA获得的逼近前沿Fig.8 Approximated fronts obtained by NSGA-Ⅱ and CEDA

5 结 论

本文设计了一种CEDA算法。在CEDA中,首先利用凝聚层次聚类算法将种群划分为若干个局部类,从每一个局部类中随机选择一个个体构成一个全局类,然后为每个个体构建一个高斯模型(此高斯模型的均值为个体本身,协方差矩阵为个体所在局部类的协方差矩阵或者是全局类的协方差矩阵)去逼近种群结构,并抽样产生新个体。此新解产生方法充分地考虑了多目标优化问题的规则特性,其本质是为每个个体添加了一个外部扰动,能改善已有的大部分分布估计算法中存在的异常个体处理不合理,种群多样性容易丢失的问题。并且处于同类中的个体共享协方差矩阵用于建模,极大地降低了建模的计算开销。

以具有复杂Pareto前沿和复杂Pareto解集形状的多目标优化测试题为求解对象,将CEDA与典型的MOEAs进行了对比实验。实验结果表明,CEDA对于此类问题具有优异的求解性能。将CEDA算法应用于齿轮减速器优化设计中,结果表明,CEDA算法同样能够快速有效地求解此类复杂的实际工程问题。

[1] ZHOU A, QU B Y, LI H, et al. Multiobjective evolutionary algorithms: a survey of the state of the art[J]. Swarm & Evolutionary Computation, 2011, 1(1):32-49.

[2] DEB K, BEYER H G. Self-adaptive genetic algorithms with simulated binary crossover[J].Evolutionary Computation,2001,9(2):197-221.

[3] SCHAER J D. Multiple objective optimization with vector evaluated genetic algorithms[C]∥Proc.of the International Conference on Genetic Algorithms and Their Applications, 1985: 93-100.

[4] MARTí L, GRIMME C, KERSCHKE P, et al. Averaged Hausdorff approximations of pareto fronts based on multiobjective estimation of distribution algorithms[C]∥Proc.of the Companion Publication of the Annual Conference on Genetic and Evolutionary Computation, 2015:1427-1428.

[5] PELIKAN M, SASTRY K, GOLDBERG D E. Multiobjective estimation of distribution algorithms[C]∥Proc.of the Scalable Optimization Via Probabilistic Modeling, 2006:223-248.

[7] ZHANG Q, ZHOU A, JIN Y. RM-MEDA: a regularity model-based multiobjective estimation of distribution algorithm[J]. IEEE Trans.on Evolutionary Computation, 2008, 12(1): 41-63.

[8] BOSMAN P A, THIERENS D. Multi-objective optimization with diversity preserving mixture-based iterated density estimation evolutionary algorithms[J]. International Journal of Approximate Reasoning, 2002, 31(3): 259-289.

[9] PELIKAN M, SASTRY K, GOLDBERG D E. Multiobjective hBOA, clustering, and scalability[C]∥Proc.of the 7th Annual Conference on Genetic and Evolutionary Computation, 2005: 663-670.

[10] SASTRY K, GOLDBERG D E, PELIKAN M. Limits of scalability of multiobjective estimation of distribution algorithms[C]∥Proc.of the IEEE Congress on Evolutionary Computation, 2005: 2217-2224.

[11] SHIM V A, TAN K C, CHEONG C Y. A hybrid estimation of distribution algorithm with decomposition for solving the multiobjective multiple traveling salesman problem[J]. IEEE Trans.on Systems, Man, and Cybernetics, Part C(Applications and Reviews), 2012, 42(5): 682-691.

[12] CHENG R, JIN Y, NARUKAWA K, et al. A multiobjective evolutionary algorithm using Gaussian process-based inverse modeling[J]. IEEE Trans.on Evolutionary Computation, 2015, 19(6): 838-856.

[13] ZHOU A, ZHANG Q, JIN Y. Approximating the set of Pareto-optimal solutions in both the decision and objective spaces by an estimation of distribution algorithm[J]. IEEE Trans.on Evolutionary Computation, 2009, 13(5): 1167-1189.

[14] WANG Y, XIANG J, CAI Z. A regularity model-based multiobjective estimation of distribution algorithm with reducing redundant cluster operator[J]. Applied Soft Computing, 2012, 12(11): 3526-3538.

[15] LI Y, XU X, LI P, et al. Improved RM-MEDA with local learning[J]. Soft Computing, 2014, 18(7): 1383-1397.

[16] LI K, KWONG S. A general framework for evolutionary multiobjective optimization via manifold learning[J]. Neurocomputing, 2014, 146(1): 65-74.

[17] XU R,WUNSCH D. Clustering[M]. New Jersey: Wiley,2008.

[18] BEUME N, NAUJOKS B, EMMERICH M. SMS-EMOA: multiobjective selection based on dominated hypervolume[J]. European Journal of Operational Research, 2007, 181(3): 1653-1669.

[19] ZITZLER E, THIELE L, LAUMANNS M, et al. Performance assessment of multiobjective optimizers: an analysis and review[J]. IEEE Trans.on Evolutionary Computation, 2003, 7(2): 117-132.

[20] ZHANG H, ZHOU A, SONG S, et al. A self-organizing multiobjective evolutionary algorithm[J], IEEE Trans.on Evolutionary Computation, 2016, 20(5): 792-806.

[21] DEB K, PRATAP A, AGARWAL S, et al. A fast and elitist multiobjective genetic algorithm: NSGA-Ⅱ[J]. IEEE Trans.on Evolutionary Computation, 2002, 6(2): 182-197.

[22] JIN Y, SENDHOFF B. Connectedness, regularity and the success of local search in evolutionary multi-objective optimization[C]∥Proc.of the IEEE Congress on Evolutionary Computation, 2003: 1910-1917.

[23] ZHOU A, ZHANG Q, JIN Y, et al. A model-based evolutionary algorithm for bi-objective optimization[C]∥Proc.of the IEEE Congress on Evolutionary Computation, 2005: 2568-2575.

[24] ZITZLER E, THIELE L. Multiobjective evolutionary algorithms: a comparative case study and the strength Pareto approach[J].IEEE Trans.on Evolutionary Computation,1999,3(4):257-271.

[25] LIU H L, GU F, CHEUNG Y. T-MOEA/D: MOEA/D with objective transform in multi-objective problems[C]∥Proc.of the International Conference on Information Science and Management Engineering, 2010: 282-285.

[26] FARHANG-MEHR A, AZARM S. Entropy-based multi-objective genetic algorithm for design optimization[J]. Structural & Multidisciplinary Optimization, 2002, 24(5): 351-361.

[27] AZARM S, TITS A, FAN M. Tradeoff driven optimization-based design of mechanical systems[C]∥Proc.of the Symposium on Multidisciplinary Analysis and Optimization, 1989: 551-558.