基于高阶累积量和小波变换的调制识别算法

谭晓衡, 褚国星, 张雪静, 杨 扬

(1. 重庆大学生物感知与智能信息处理重庆市重点实验室, 重庆 400044; 2. 重庆大学通信工程学院, 重庆 400044; 3. 安徽四创电子股份有限公司, 安徽 合肥 230001)

0 引 言

随着信息与通信领域的快速发展,为了能够充分地利用信道以及满足实际需求,在同一个通信系统中会同时采用多种数字调制方式。因此,数字调制信号的自动识别技术有十分重要的研究意义,该技术的主要任务是识别调制方式,从而实现调制信号的智能接收、处理。尤其是在非协作通信领域,调制识别有着重要的应用[1]。由于高阶累积量和小波变换对噪声都有一定程度的抑制作用,这两种方法在数字调制识别中应用广泛。

文献[2]提出通过四阶和六阶的高阶累积量对多进制数字相位调制(M-ary phase shift keying,MPSK)和多进制正交幅度调制(M-ary quadrature amplitude modulation,MQAM)两种调制信号的识别方法,应用了支持向量机(support vector machine,SVM)作为分类器,讨论了信噪比对识别性能的影响。文献[3]提出基于累积量和谱特征对卫星通信信号调制方式MPSK、MQAM、最小频移键控(minimum shift keying,MSK)的识别方法,并分析了升余弦滤波对识别结果产生的影响。文献[4]提出基于四阶、六阶高阶累积量,应用支持向量机作为分类器,实现了多进制数字振幅调制(M-ary amplitude shift keying,MASK)、MPSK、多进制数字频率调制(M-ary frequency shift keying,MFSK)、16进制正交幅度调制(16-ary quadrature amplitude modulation,16QAM)的分类方法。但是该算法未能将特征参数完全相同的2进制振幅调制(2-ary amplitude shift keying,2ASK)和2进制相位调制(2-ary phase shift keying,2PSK)信号区分,应用受限。文献[5]提出基于四阶累积量实现MPSK和MQAM在多径衰落信道的识别方法。文献[6]提出了一种基于高阶谱、循环谱和时频特征的组合特征提取与识别方法。除常见信号外,还对直接序列展频(direct sequence spread spectrum,DSSS)信号进行了识别。文献[7]提出一种新的分类方法,基于高积累积量完成在高斯信道和衰落信道下MPSK、MQAM的识别。文献[8]提出基于高阶累积量提取特征参数,设计分类器时应用了蚁群算法。文献[9]提出基于小波消噪后的瞬时特征参数,完成2ASK、2进制频率调制(2-ary frequency shift keying,2FSK)、2PSK、4进制相位调制(4-ary phase shift keying,4PSK)、4进制振幅调制(4-ary amplitude shift keying,4ASK)、4进制频率调制(4-ary frequency shift keying,4FSK)的识别。文献[10]提出利用信号小波包变换的方差、第四阶矩和过零率等特征参量完成MPSK、MQAM信号的分类方法。以上基于高阶累积量、小波变换以及联合其他特征参数的方法中,不能完全识别MASK、MPSK、MFSK和MQAM这4类数字调制方式,或者提取特征参数较多,算法较为复杂。

基于高阶累积量和小波变换提取特征参数,实现了一种混合识别算法,并用软件进行仿真验证。首先模拟现实接收机场景,产生各类信噪比较低的调制信号,然后从调制信号的累积量和小波变换后提取特征参数,利用神经网络分类器实现2PSK、4PSK、8进制相位调制(8-ary phase shift keying,8PSK)、2ASK、4ASK、2FSK、4FSK、8进制频率调制(8-ary frequency shift keying,8FSK)、16QAM、64进制正交幅度调制(64-ary quadrature amplitude modulation,64QAM)的分类。该算法充分利用了高阶累积量和小波变换抗噪性能良好的优点,扩大了能识别的调制方式的范围,提升了识别率,减少了特征参数的个数,降低了算法复杂度。理论分析和仿真结果表明,该算法能有效地对文中10种数字调制方式进行识别,并有较好的识别效果。

1 高阶累积量和小波变换识别分析

1.1 信号模型

被噪声污染的数字调制信号的复数形式[11]可表示为

(1)

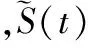
根据数字调制信号的性质,可以将下变频后的各类调制信号[11]表示为

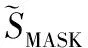
(2)

(3)

ωi∈{(2m-1-M)Δω,m=1,2,…,M}

(4)

Ei=ai+bi,φi=arctan(bi/ai)mod2π

(5)

式中,E为发送码元波形的能量;M为调制阶数;Ts为符号周期;p(t)是发送码元波形;Δω为FSK信号的频偏;ai,bi为QAM的信号同相正交分量。

1.2 高阶累积量理论

对于一个零均值的k阶平稳随机过程x(t),其k阶累积量的定义[1]为

Ckx(f1,f2,…,fk-1)=

Cum(x(t),x(t+f1),…,x(t+fk-1))

(6)

式中,Cum(·)的含义为对其求累积量。

随机过程x(t)的p阶混合矩[1]为

Mpq=E{[x(t)p-qx*(t)q]}

(7)

由此可得,零均值的平稳随机过程x(t)的各阶累积量的表达式[12]为

C20=Cum(x,x)=M20

(8)

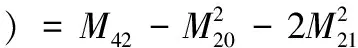
(9)

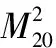
(10)

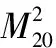
(11)

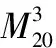
(12)

C61=Cum(x,x,x,x,x,x*)=

(13)

若x(t)为高斯过程,则高于二阶累积量将恒等于0,因此高阶累积量具有良好抑制高斯噪声的特性。将各调制信号式(2)～式(5)代入到高阶累积量的计算式中,可得各类数字调制信号的高阶累积量的理论值,如表1所示。

表1 数字调制信号累积量的理论值

注:E为调制信号能量。

从式(2)和式(3)中可以得到,2ASK、2PSK的基带信号是等效的,不能通过高阶累积量区分。从表1中可以看到,8PSK、MFSK以及MFSK的类内识别也无法区分。16QAM、64QAM的各阶累积量较为接近,也不便于利用高阶累积量区分。在此,引入数字调制的信号的小波变换来提取参数。

1.3 数字信号小波变换后的参数提取

小波变换(wavelet transform,WT)是一种多分辨率的时间、频率分析方法,同时通过变换尺度参数和位移参数可以实现时域和频域的局部观测。利用WT把信号在不同尺度下分解,能呈现各种调制类型信号的细节,因此WT可以应用到数字信号的调制类型识别中。

在任意L2(R)空间中的函数s(t)的连续WT定义[1]为

(14)

(15)

用不同的小波基分析同一个问题会产生不同的结果,常见的小波函数有:哈尔(Haar)小波、多贝西(Daubechies)小波、莫雷(Morlet)小波等。考虑到Haar小波计算简单,且对瞬时时变信号检测能力较强,根据遇到的实际问题出发,选用Haar小波。

Haar小波定义为

(16)

Haar小波对噪声有较好的抑制作用,各类调制信号在同一码元内的WT可以表示[11]为

(17)

(18)

CWTMFSK(a,τ)=

(19)

(20)

2 算法设计

2.1 基于高阶累积量的特征参数

为了实现数字信号的调制识别,首先利用基于数字信号高阶累积量的特征参数T1，表达式为

T1=|C61|/|C42|

(21)

参数T1选取比值和绝对值的形式,可以分别消除信号的幅度和相位抖动对累积量的影响,且不会因信号星座图平移、尺度和相位旋转变化而变化。各类数字调制类型的特征参数T1的理论值如表2所示。

表2 数字调制信号特征参数T1的理论值

从表2可知，参数T1直接将信号区分为{2PSK,2ASK},{4ASK},{4PSK}, {8PSK, 2FSK, 4FSK,8FSK}, {16QAM, 64QAM}几类,减少了特征参数的个数,精简了算法,且有较高的抗干扰性。

{8PSK}和{MFSK}、{MFSK}的类内识别、{2ASK}和{2PSK}、{16QAM}和{64QAM}的区分由于T1值相同或接近,无法应用高阶累积量参数。

2.2 基于WT的特征参数

步骤1将式(17)～式(20)分别取绝对值后,可得数字信号WT后的幅度值。经过中值滤波,消除相位突变产生的尖峰后,如图1所示。

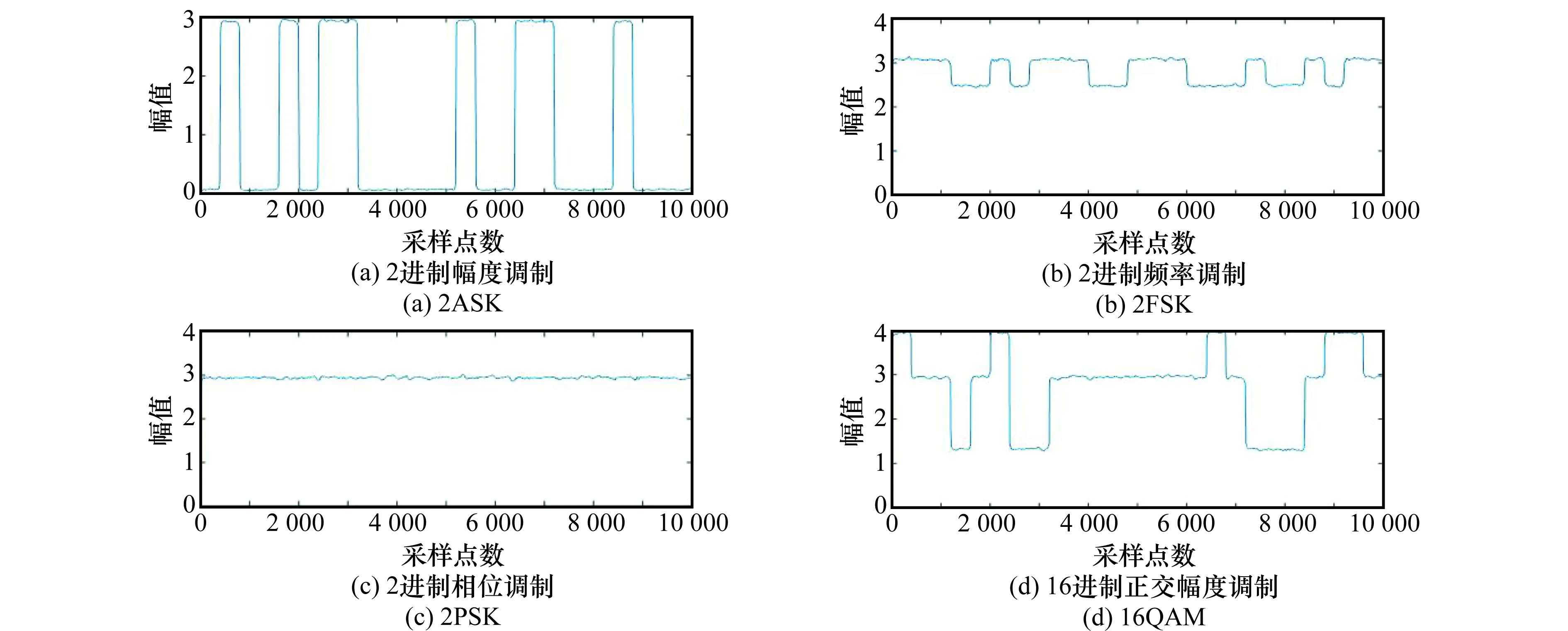
图1 调制信号WT后幅度值Fig.1 Amplitude of modulation signals after WT

由图1可知,数字信号的WT区间在同一码元内时,WT的幅度值是恒定的。MPSK信号WT后的幅度值为一个常数;MFSK信号的WT幅度与fi有关;MASK和MQAM信号WT后的幅度与该码元的幅度有关。所以,除了MPSK信号,其他MASK、MFSK、MQAM信号的WT后的幅度值都为多幅度函数。所以,可以通过WT后的幅度值的直方图波峰个数作为特征参数T2,来区分{2ASK},{2PSK}。

由图1还可知,MQAM信号的WT幅度值也为多幅度函数,幅度种类由MQAM信号阶数决定。由其星座图(以更为一般的方形星座图为例,不影响识别结果)可知,16QAM信号的WT幅度值种类为3,64QAM信号WT幅度值种类为9。所以也可以通过特征参数T2来区分{16QAM},{64QAM}。各类数字调制类型的特征参数T2理论值如表3所示。

表3 数字调制信号特征参数T2的理论值

因为MFSK信号的小波幅度呈现阶梯状,阶梯个数表征了MFSK的调制阶数,所以，{MFSK}的类内识别也可以通过特征参数T2实现。然而,MFSK信号小波幅度与未调频率fi有关,当MFSK的调制指数较小时,相邻符号的小波幅度差也较小,在信噪比较低的条件下,直方图波峰间相互混叠,识别难度较大。

步骤2文献[11]提出了一种利用小波变换频率信息的MFSK类内识别方法,通过对式(19)提取其相位信息,并计算出频率。该种方法比直接提取信号频率信息抗噪声能力要强很多。提取到的频率信息的直方图如图2所示。

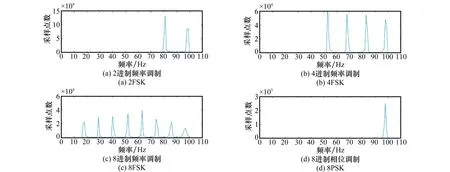
图2 调频信号WT后瞬时频率的直方图Fig.2 Histogram of instantaneous frequency after WT of FSK signal

在此选取调制信号WT频率信息的直方图波峰个数作为特征参数T3,来区分{8PSK},{MFSK}及{MFSK}的类内识别。各类数字调制类型的特征参数T3的理论值如表4所示。

表4 数字调制信号特征参数T3的理论值

2.3 基于神经网络的分类器设计

分类器的设计可以使用各种智能分析工具,如神经网络,它能在多重次元的情况下,通过神经网络的多层感知器类型对非线性问题模型进行高效构建[13]。反向传播(back propagation,BP)神经网络是一种多层前馈神经网络,由于其结构简单,可塑性强,在神经网络中应用更为广泛。BP神经网络分为输入层、隐含层和输出层,本文选用单隐含层BP网络作为调制识别算法的分类器。

BP神经网络进行调制识别时,主要分为训练过程和识别过程。首先，将训练样本输入神经网络,经过输入层、隐含层和输出层,得到实际输出,与理论输出进行比较得到误差；再将误差反向传播,按照减小误差的原则,修正隐含层至输出层、输入层至隐含层的连接权值和节点阈值,并不断循环这个过程,直到误差最小或达到最大训练次数,即为训练过程;计算待分类的数字调制信号的特征参数,送入已经训练好的神经网络,即为识别过程。

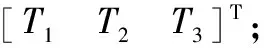
3 性能与仿真

本文使用Matlab软件对算法进行仿真分析,首先产生模拟接收机接收到的受噪声污染的各调制信号,然后进行以下4个步骤。

步骤1研究不同信噪比(signal-to-noise, SNR)下接收信号特征参数的变化情况。

步骤2对比不同SNR下算法的识别结果。

步骤3与其他文献算法的复杂度比较。

步骤4与基于高阶累积量算法、基于小波变换算法的性能比较。

3.1 仿真实验1 特征参数随信噪比的变化情况

本算法的仿真条件设置为:载波频率10 kHz,采样频率200 kHz,符号速率500 bit/s,有10种待识别数字调制信号,分别为2ASK、4ASK、2FSK、4FSK、8FSK、2PSK、4PSK、8PSK、16QAM和64QAM。噪声选取为高斯白噪声,SNR分别从0～20 dB中选取。

特征参数T1随信噪比变化的值如图3所示,可以看出,T1在SNR>-2 dB时便较为稳定。如第2节所述,可以顺利将信号分成5类,且各类信号间区别明显。证明了特征参数T1的正确性。

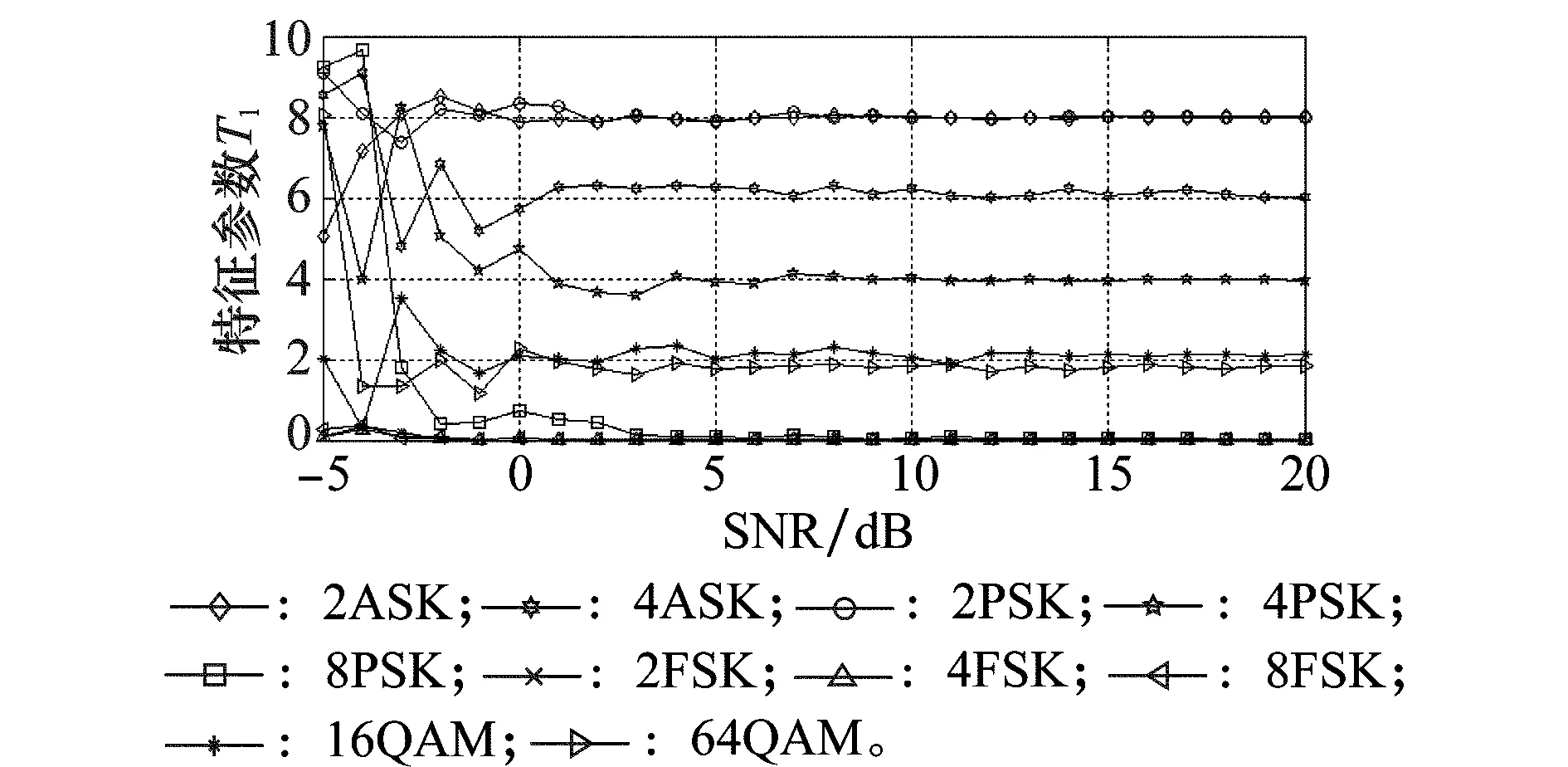
图3 特征参数T1随SNR变化的值Fig.3 Characteristic parameters T1 with SNR changing

特征参数T2随SNR变化的值如图4所示。可以看出2ASK、2PSK、16QAM在SNR大于-5 dB时即可识别出,64QAM的识别对SNR要求稍高,到0 dB以上即可识别出。证明了特征参数T2的正确性。

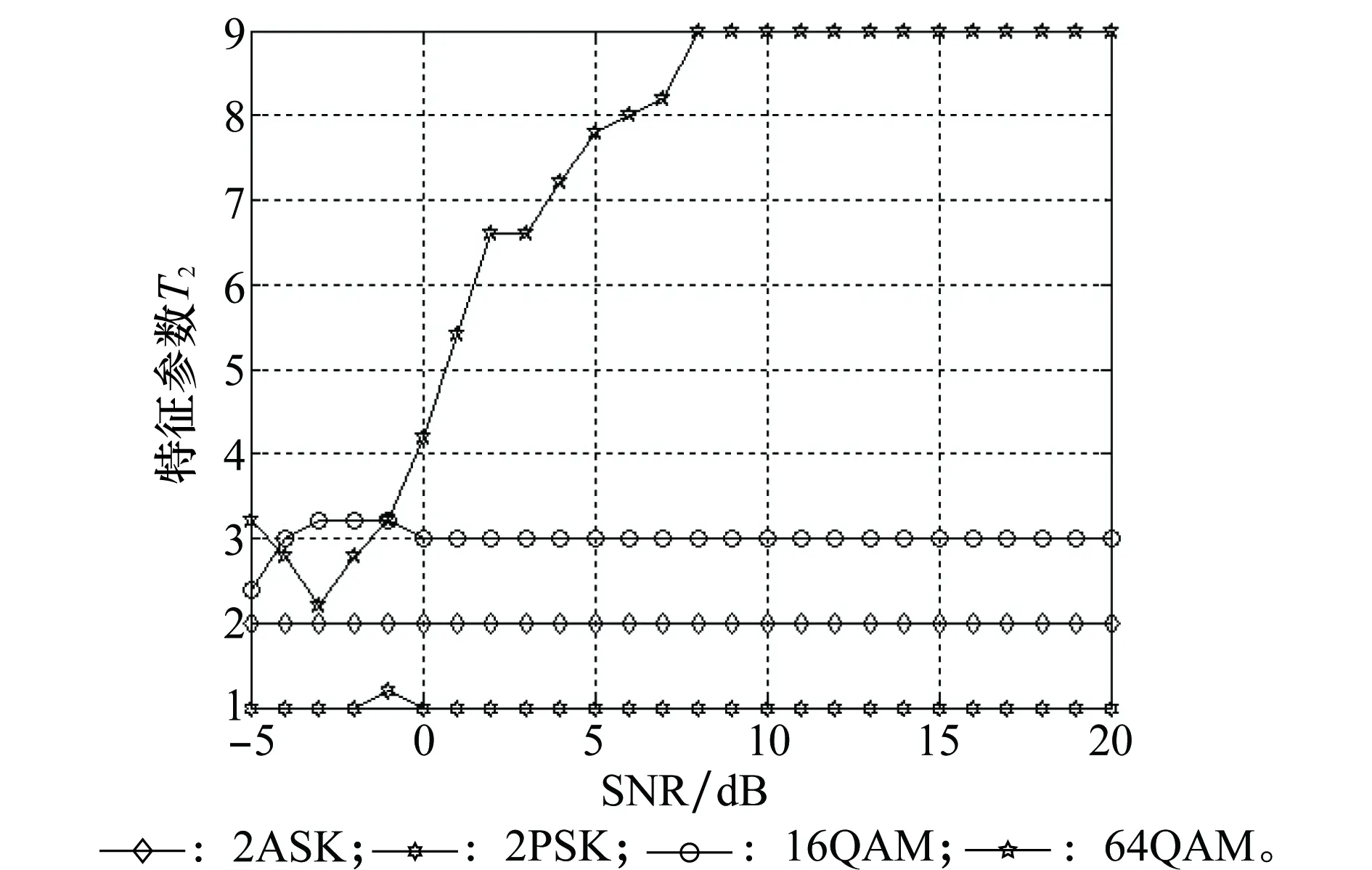
图4 特征参数T2随SNR变化的值Fig.4 Characteristic parameters T2 with SNR changing

特征参数T3随SNR变化的值如图5所示。可以看出2FSK、4FSK、8PSK在SNR大于-2 dB时即可识别出,8FSK的识别对SNR要求稍高,到1 dB以上即可识别出。证明了特征参数T3的正确性。

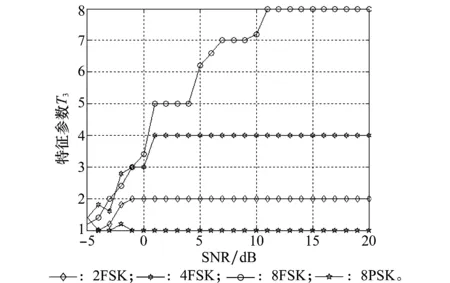
图5 特征参数T3随SNR变化的值Fig.5 Characteristic parameters T3 with the SNR changing

3.2 仿真实验2 算法综合性能的研究

为了测试算法在不同SNR下的识别效果,噪声选取为高斯白噪声,在SNR为-2～20 dB时,每隔1 dB每种调制方式生成50组样本,送入BP网络分类器中进行训练[15],在SNR未知的情况下,训练BP神经网络分类器10次,得到10个网络。另外,在-2 dB到5 dB、10 dB、15 dB、20 dB生成100组样本进行测试,训练和测试时每个SNR在10个网络进行测试,即每种调制方式仿真100×10次,识别结果如表5和图6所示。

表5 不同SNR下的识别结果

从实验结果可知,每种调制方式的正确识别率在SNR≥1 dB时均超过90%,而在SNR≥2 dB时均可达到98%及以上,且从整体上看,识别效果随SNR增大而提升。

3.3 仿真实验3 与其他文献算法的复杂度比较

本算法能够实现MASK、MPSK、MFSK和MQAM 4类调制方式的有效识别,与其他文献比较,文献[12]采用结合高阶累积量和循环谱的混合识别算法,应用神经网络对信号进行识别,识别结果为在SNR>5 dB时,除64QAM外,识别率在98%以上。在算法复杂度相近的情况下,本文提出的算法在低SNR下识别率显著提高。

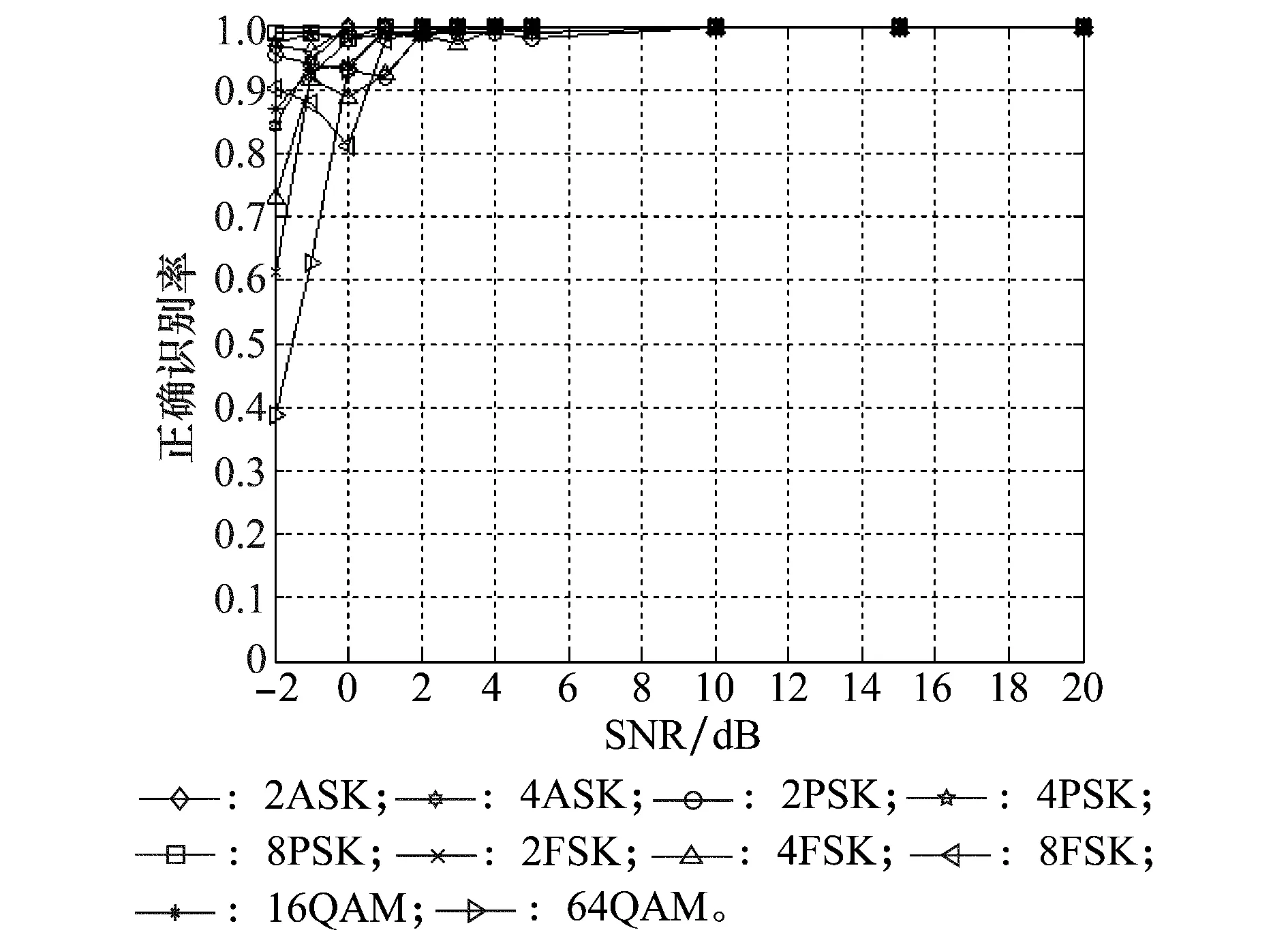
图6 不同SNR下的识别结果Fig.6 Result of recognition with SNR changing

文献[15]中,利用调制信号的高阶累积量和时域瞬时信息,并结合星座图特征进行特征提取,对神经网络进行识别，识别结果为SNR>0 dB时,识别率在98%以上。

但文献[15]中方法要求用11个特征参数,实现过程复杂,本文算法将特征参数减少到3个,有效降低了算法复杂度,更具工程应用性。对比结果如表6所示。

表6 与其他文献结果对比

3.4 仿真实验4 算法间的性能比较

因部分调制方式的高阶累积量相同,所以只使用高阶累积量提取特征参数时,需要引入瞬时幅度特征区分2PSK和2ASK,将信号微分后再计算高阶累积量以区分MFSK。只使用高阶累积量提取3个特征参数的调制识别算法结果,如图7所示。

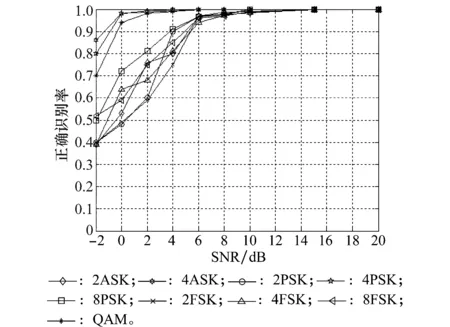
图7 基于高阶累积量算法的识别结果Fig.7 Recognition results based on higher order cumulants

利用WT进行调制方式的类间识别时,特征参数通常选择WT幅度的方差。再选择WT的幅度和频率的直方图峰值个数进行类内识别。只应用WT提取3个特征参数的调制识别算法结果,如图8所示。

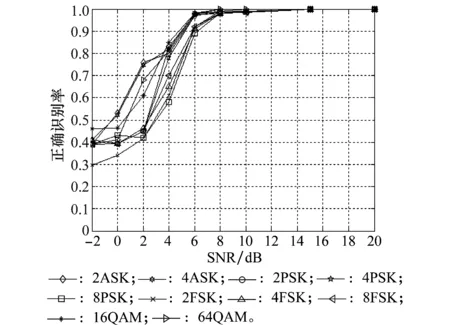
图8 基于WT算法的识别结果Fig.8 Recognition results based on WT

对比图6与图7、图8可以看到,本文提出的基于高阶累积量和WT的联合调制识别算法的性能,优于单独应用一种算法的性能。这是因为单独使用高阶累积量算法引入的特征参数,受噪声的影响明显。同样,在低SNR下,选取WT幅度的方差作为特征参数进行类间识别时,效果不理想。

4 结 论

本文基于高阶累积量和WT提取的3个特征参数,实现了10种数字调制方式的自动识别,计算量小,且优于单独使用高阶累积量或WT的方法,并采用神经网络进行分类,在低SNR下取得了较好的识别率,在整体上获得了较好的识别性能。

[1] 杨杰,刘珩,卜祥元,等.通信信号调制识别:原理与算法[M].北京:人民邮电出版社,2014.

YANG J, LIU H, BU X Y, et al. Modulation recognition for communication signals: principles and algorithms[M]. Beijing: Posts and Telecom Press, 2014.

[2] LI P H, ZHANG H X, WANG X Y. Modulation recognition of communication signals based on high order cumulants and support vector machine[J]. The Journal of China Universities of Posts and Telecommunications, 2012,19(11):61-65.

[3] 马兆宇,韩福丽,谢智东.卫星通信信号体系调制识别技术[J].航空学报,2014,35(12): 3403-3414.

MA Z Y, HAN F L, XIE Z D. Modulation recognition technology of satellite communication signal system[J]. Acta Aeronautica et Astronautica Sinica, 2014,35(12): 3403-3414.

[4] ZHAO Y, XU Y T, JIANG H, et al. Recognition of digital modulation signals based on high-order cumulants[C]∥Proc.of the International Conference on Wireless Communications & Signal Processing,2015:432-436.

[5] CHANG D C, SHIH P K. Cumulants-based modulation classification technique in multipath fading channels[J]. IET Communications, 2015, 9(6): 828-835.

[6] LIU H D, ZHANG H X, HE P F. Study on hybrid pattern recognition algorithm for modulated signals[J]. The Journal of China University of Posts and Telecommunications,2014,21(14):106-109.

[7] ABDELMUTALAB A, ASSALEH K, EI-TARHUNI M. Automatic modulation classification based on high order cumulants and hierarchical polynomial classifiers[J]. Physical Communication, 2016, 21(4): 10-18.

[8] EBRAHIMZADEH A, GHAZALIAN R. Blind digital modulation classification in software radio using the optimized classifier and feature subset selection[J]. Engineering Applications of Artificial Intelligence, 2014, 24(1): 50-59.

[9] GU X Y. Research on modulation recognition algorithm of digital communication signal based on wavelet denoising[J]. Applied Mechanics and Materials, 2014, 608(10): 459-467.

[10] EBRAHIMZADEH A, AZIMI H, MIRBOZORGI S. A digital communication signals identification using an efficient recognizer[J]. Measurement, 2011, 44(8): 1475-1481.

[11] 汤卫东.基于小波变换的数字通信信号调制识别研究[D].西安: 西安电子科技大学, 2010.

TANG W D. Research on modulation recognition of digital communication signals based on wavelet transform[D]. Xi’an: Xidian University, 2010.

[12] 赵雄文,郭春霞,李景春.基于高阶累积量和循环谱的信号调制方式混合识别算法[J].电子与信息学报,2016,38(3):674-680.

ZHAO X W, GUO C X, LI J C. Mixed recognition algorithm for signal modulation schemes by high-order cumulants and cyclic spectrum[J]. Journal of Electronics & Information Technology, 2016,38(3):674-680.

[13] ADZHEMOV S S, TERESHONOK M V, CHIROV D S. Type recognition of the digital modulation of radio signals using neural networks[J]. Moscow University Physics Bulletin, 2015, 70(1): 22-27.

[14] WONG M L D, NANDI A K. Automatic digital modulation recognition using artificial neural network and genetic algorithm[J]. Signal Processing, 2004, 84(2): 351-365.

[15] 谭晓衡,陈印.基于联合特征参数的数字调制识别优化算法[J].系统工程与电子技术,2011,33(12): 2733-2736.

TAN X H, CHEN Y. Automatic digital modulation recognition based on combined feature parameters[J]. Systems Engineering and Electronics, 2011, 33(12): 2733-2736.