基于软符号重构的迭代子载波间干扰补偿方法
2018-01-15张慧敏刘海涛
王 磊, 张慧敏, 从 婉, 刘海涛
(中国民航大学智能信号与图像处理天津市重点实验室, 天津 300300)
0 引 言
L频段数字航空通信系统(L-band digital aeronautical communication system, L-DACS)是民航新一代空中交通管理系统的重要通信基础设施[1]。L-DACS系统存在两种候选技术方案,即L-DACS1与L-DACS2。两种技术方案相比,L-DACS1具有频谱利用率高、抗多径衰落能力强及传输容量大等优点,因此获得航空制造界与学术界的广泛关注,该系统被视为民航未来航空数据链系统的重要技术手段[2-3]。为解决航空数据链系统频率资源匮乏的问题,国际民航组织(international civil aviation organization,ICAO)提出将L-DACS系统部署在航空无线电导航L频段的建议,其中,L-DACS1系统的频谱内嵌在民航陆基测距机(distance measuring equipment,DME)的波道间,2007年世界无线电大会批准了ICAO的建议。由于L-DACS1系统的频谱与DME系统频谱存在部分重叠,而DME信号又是大功率的脉冲信号,因此对于L-DACS1系统正交频分复用(orthogonal frequency division multiplexing, OFDM)接收机来说,DME信号就成了影响其系统性能的带内干扰。文献[4-6]表明,如果L-DACS1系统OFDM接收机不采取干扰抑制措施,系统的性能将显著恶化,误码率增大,有可能造成空地链路通信失效,因此,在工程实际中必须要考虑OFDM接收机的脉冲干扰问题。
L-DACS1系统DME脉冲干扰抑制方法主要包括:非线性脉冲熄灭方法[7-10]、脉冲重构干扰抑制方法[11-12]和基于阵列天线空域滤波方法[13-14]。相对于其他干扰抑制方法,非线性脉冲熄灭法具有运算复杂度低、工程实现简便及适用性强的优点。因此,L-DACS1系统技术规范建议使用脉冲熄灭法来抑制DME干扰[15]。虽然脉冲熄灭法在一定程度上可以提高L-DACS1系统链路传输的可靠性,但需要考虑两个关键问题,即脉冲熄灭最佳门限如何设置及脉冲熄灭后带来的子载波间干扰(inter carrier interference, ICI)问题。为解决OFDM接收机中脉冲熄灭方法的最佳门限设置问题,文献[16]给出了脉冲熄灭自适应门限设置方法。为抑制脉冲熄灭导致的ICI问题,文献[17]提出了基于硬判决的迭代ICI补偿方法,仿真表明,所提出方法可提高链路传输可靠性,但由于硬判决方法固有的错误传播现象,因此对OFDM接收机符号差错性能的改善有限。
为了抑制脉冲熄灭法产生的ICI干扰,提高OFDM接收机的链路可靠性,提出了基于软符号重构的迭代ICI时域补偿方法(以下简称软符号重构法)。实施步骤如下:首先,接收机译码器输出的码字比特软信息通过交织与重构得到发送符号的软估计值;然后利用该软估计值和信道频率响应可以重构出接收信号的时域波形;最后对熄灭信号样值进行时域补偿。仿真结果表明:软符号重构法可克服硬判决迭代ICI干扰抑制方法存在的错误传播现象,有效消除脉冲熄灭产生的ICI,提高L-DACS1系统OFDM接收机的可靠性。此外,相对于正常的接收机,所提出方法的运算复杂度仅增加一倍,因此该方法可应用于实际系统。
论文具有两个方面的贡献:一是提出了基于软符号重构的迭代ICI抑制方法;二是提出了软符号重构的计算方法。
1 软符号重构法迭代ICI抑制接收机
1.1 迭代ICI干扰抑制OFDM接收机框架
首先,L-DACS1系统的OFDM接收机将L波段的射频信号经变频、放大和滤波后转换为模拟基带信号,然后通过A/D模块采样得到数字基带信号。为了保证DME脉冲干扰的抑制性能,在采样时采用了过采样,一般为4倍过采样方案。软符号重构法迭代ICI抑制接收机的原理框图如图1所示。

图1 软符号重构的迭代子载波间干扰抑制接收机Fig.1 Block diagram of the proposed OFDM receiver
假设接收机已建立符号定时同步,则接收机移除循环前缀后,单个OFDM符号周期内接收信号矢量表示为r=[r0,…,rn,…,rVK-1]T。
r=h⊗x+i+n
(1)
式中,V代表过采样因子;K代表OFDM系统子信道总数;h代表信道冲激响应矢量;x代表发射信号矢量;i代表信道输入的DME干扰信号矢量;n代表信道输入的复高斯白噪声矢量。
接收信号矢量r分成两路,一路送入DME干扰检测器检测是否存在DME干扰,如果接收信号存在DME干扰,则进一步送入脉冲位置估计器计算DME干扰出现的位置[8],同时将含有DME干扰的样值序号存放在集合Ω中,即Ω={n|rn包含DME噪声,n=0,1,…,VK-1}。另一路接收信号矢量r则送入脉冲熄灭器消除脉冲干扰后,相应地输出信号矢量表示为y=[y0,y1,…,yn,…,yVK-1]T。
y=D·r
(2)
式中,D=diag(d0,d1,…,dn,…,dVK-1)代表脉冲熄灭矩阵,当接收信号矢量r中第n个样值含有DME干扰时,dn取值为0;否则,dn取值为1。脉冲熄灭器输出信号矢量y进一步送入ICI干扰补偿器对子载波间干扰进行补偿,ICI干扰补偿器输出信号矢量记为z=[z0,z1,…,zn,…,zVK-1]T,其第n个样值zn表示为
(3)

Yov=F·z
(4)

(5)


(6)
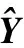
(7)
式中,F-1代表VK点的离散傅里叶逆变换矩阵。当迭代ICI干扰补偿方法收敛后,译码器输出的信息比特后验软信息LDes送入硬判决器进行判决可得到发送比特序列的估计值。
1.2 测距仪干扰检测方法
图2给出OFDM与DME信号频谱重叠示意图,横坐标为频率,纵坐标为功率,信号干扰比(signal to interference ratio, SIR)=-4 dB,fc=±500 kHz。图2中黑色实线表示OFDM信号频谱,蓝色虚线表示滤波后的DME信号频谱。由图2可观测到:OFDM信号能量主要集中在-250~+250 kHz波段,而DME信号的大部分能量则位于±250 kHz附近。基于此,通过比较信号在频率±250 kHz及直流子信道附近平均功率的大小,就可以检测接收信号中是否含有DME干扰。

图2 OFDM信号与DME信号频谱重叠示意图(SIR=-4 dB,fc=±500 kHz) Fig.2 Spectrum overlaps of OFDM and DME signal(SIR=-4 dB,fc=±500 kHz)
(8)
(9)
(10)

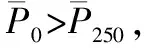
1.3 软符号解调方法
软符号解调器第k个子信道输入信号Yk表示为
Yk=Hk·Xk+Nk,k=0,1,…,K-1
(11)
式中,Hk代表第k个子信道的频率响应;Xk代表第k个子信道传输的调制符号;Nk代表第k个子信道输入的噪声信号,其包括信道输入的复高斯白噪声及脉冲熄灭导致的ICI噪声。对于不同调制方式,接收机软解调的方法不相同,为方便叙述,以下以正交相移键控(quadrature phase shift keying,QPSK)调制为例来说明接收机软解调的方法。

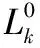
(12)
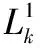
(13)
式中
(14)

1.4 软符号重构方法

(15)
(16)

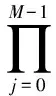
(17)
最后根据式(17)计算得到调制符号Xk取值为各个星座点的概率,调制符号Xk的软估计值为
(18)
2 仿真结果与分析
2.1 仿真参数设置
为了验证所提出的基于软符号重构的迭代ICI抑制方法的正确性,本文参考L-DACS1系统规范设计了基于软符号重构的迭代ICI抑制方法的L-DACS1系统仿真平台。主要参数设置如下:
(1) 发射机参数
卷积编码:生成多项式[171 133];
交织器深度:5 400(DATA/CC帧);
调制方式:QPSK/8PSK;
过采样因子:4;
IFFT点数:64;
有效子载波数:50;
循环前缀点数:11。
(2) 信道参数
信道类型:加性高斯白噪声(addictive white Gaussian noise,AWGN)/航空Parking信道;
DME干扰源数目:1;
脉冲出现频率:3 600(脉冲对/秒);
干扰载波偏置:500 kHz;
信干比:-4 dB。
(3) 接收机参数
等效中频滤波器:通带截止频率0.3 MHz,阻带截止频率0.6 MHz;
抗混叠滤波器:滚降因子0.25升余弦滤波器。
2.2 仿真结果分析
采用本文方法重构出来的OFDM时域波形如图3所示。仿真时设置信道类型为AWGN信道,SIR=-4 dB,信噪比(signal-to-noise ratio,SNR)=15 dB。为了便于比较,画图时忽略了DME脉冲干扰和高斯白噪声。在图3中,蓝色曲线代表进行脉冲熄灭抗干扰后的OFDM信号波形,红色曲线代表利用本文方法进行1次迭代干扰补偿后的OFDM信号波形,黑色曲线代表没有经过脉冲熄灭处理的原始OFDM信号波形。由图3可知,1次迭代干扰补偿后的OFDM信号波形(红色)与原始的OFDM信号(黑色)波形基本一致。
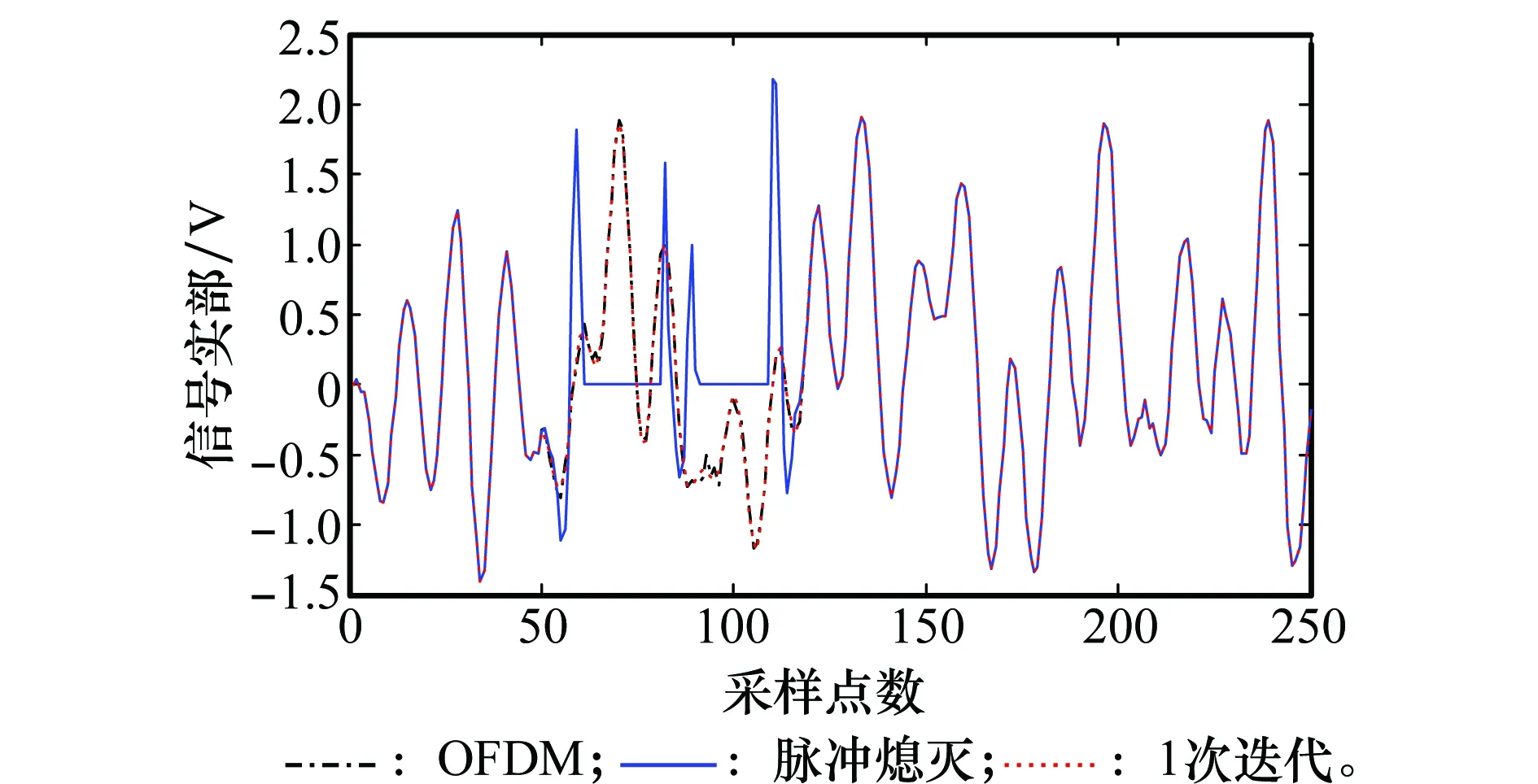
图3 重构的时域信号波形(AWGN信道,SIR=-4 dB,SNR=15 dB)Fig.3 Reconstructed time-domain signal waveform(AWGN,SIR=-4 dB,SNR=15 dB)
采用本文方法进行干扰补偿后对接收信号星座的影响进行分析和仿真,结果如图4所示。仿真时设置信道类型为AWGN信道,SIR=-4 dB,SNR=15 dB。图4(a)代表脉冲熄灭后接收信号的星座,图4(b)代表迭代1次补偿后接收信号的星座,图4(c)代表迭代2次补偿后接收信号的星座,图4(d)代表迭代3次补偿后接收信号的星座。4个星座比较表明:①本文提出方法可有效消除子载波间的干扰;②本文提出方法收敛速度快,仅需要1次迭代就能获得满意的补偿效果。
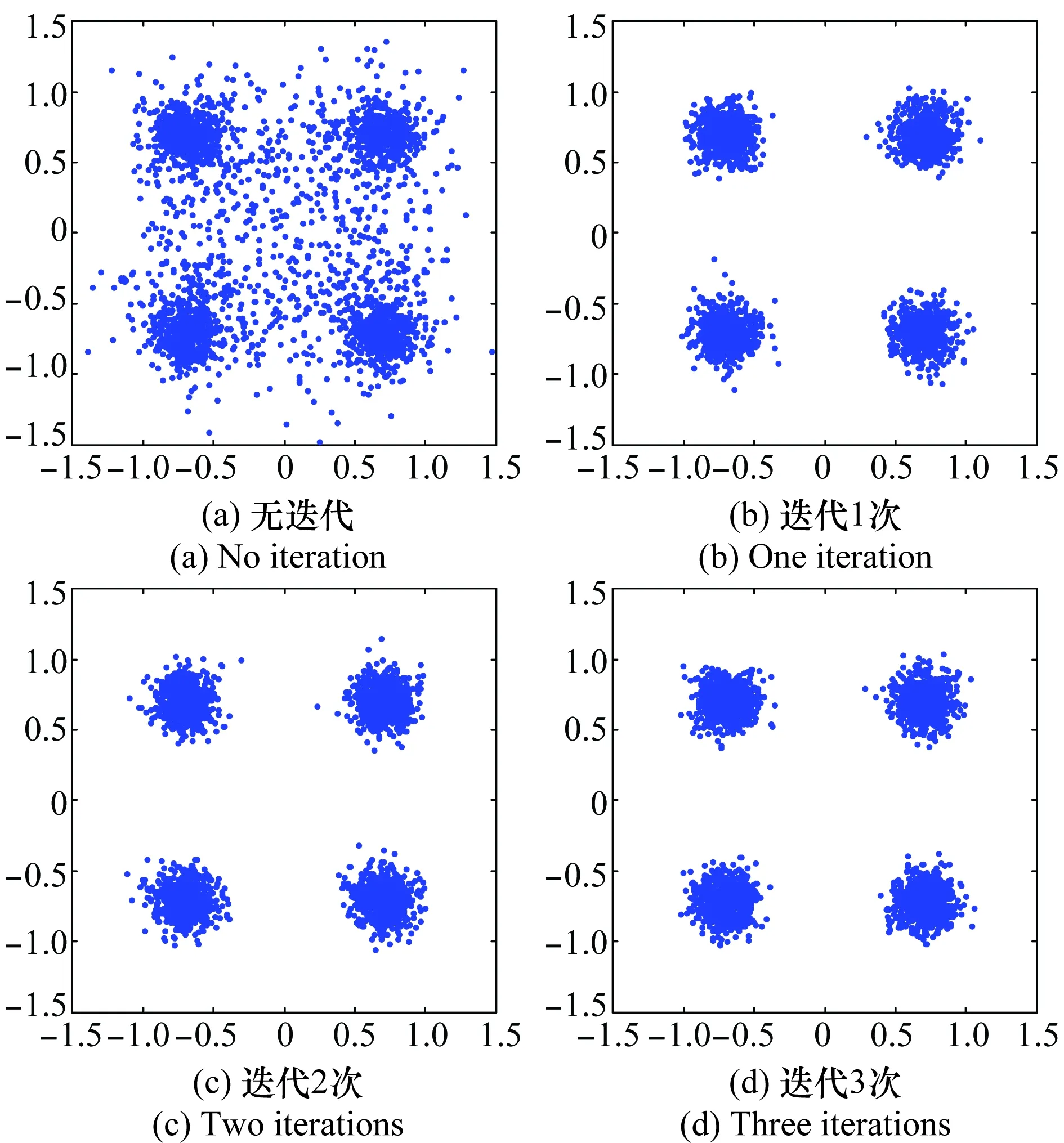
图4 解调信号星座(AWGN信道,SIR=-4 dB,SNR=15 dB)Fig.4 Constellation diagram after modulation (AWGN, SIR=-4 dB,SNR=15 dB)
图5给出了本文所提出方法的误比特率(bit error ratio, BER)曲线,仿真时设置信道类型为AWGN信道,SIR=-4 dB,OFDM信号调制方式为QPSK。其中,标有“○”的曲线是没有进行干扰抑制的BER曲线;标有“□”的曲线为脉冲熄灭法的BER曲线;标有“◇”的曲线是经过1次迭代处理后的硬判决ICI补偿法的BER曲线;标有“▽”的曲线是经过2次迭代处理后的硬判决ICI补偿法的BER曲线;标有“----◇----”的曲线代表经过1次迭代处理后的软符号重构法的BER曲线;标有“----▽----”的曲线代表经过2次迭代处理后的软符号重构法的BER曲线;标有“·”的曲线代表不存在DME干扰时的BER曲线。

图5 比特差错性能曲线(AWGN信道,QPSK,SIR=-4 dB)Fig.5 BER performance (AWGN channel, QPSK, SIR=-4 dB)
图6给出了本文所提出方法的比特差错性能曲线,仿真时设置信道类型为多径信道,SIR=-4 dB,OFDM信号调制方式为QPSK。其中,标有“○”的曲线是没有进行干扰抑制的BER曲线;标有“□”的曲线为脉冲熄灭法的BER曲线;标有“◇”的曲线代表经过1次迭代处理后的硬判决ICI补偿法的BER曲线;标有“▽”的曲线代表经过2次迭代处理后的硬判决ICI补偿法的BER曲线;标有“----◇----”的曲线代表经过1次迭代处理后的软符号重构法的BER曲线;标有“----▽----”的曲线代表经过2次迭代处理后的软符号重构法的BER曲线;标有“·”的曲线代表不存在DME干扰时的BER曲线。

图6 比特差错性能曲线(多径信道,QPSK,SIR=-4 dB)Fig.6 BER performance (multipath channel, QPSK, SIR=-4 dB)
图7给出了本文所提出方法的比特差错性能曲线,仿真时设置信道类型为多径信道,SIR=-4 dB,OFDM信号调制方式为8PSK。其中,标有“○”的曲线是没有进行干扰抑制的BER曲线;标有“□”的曲线为脉冲熄灭法的BER曲线;标有“◇”的曲线代表经过1次迭代处理后的硬判决ICI补偿法的BER曲线;标有“▽”的曲线代表经过2次迭代处理后的硬判决ICI补偿法的BER曲线;标有“----◇----”的曲线代表经过1次迭代处理后的软符号重构法的BER曲线;标有“----▽----”的曲线代表经过2次迭代处理后的软符号重构法的BER曲线;标有“·”的曲线为不存在DME干扰时的BER曲线。
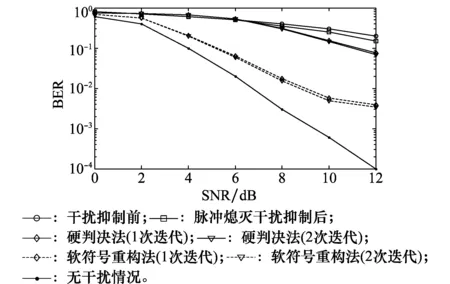
图7 比特差错性能曲线(多径信道,8PSK,SIR=-4 dB)Fig.7 BER performance (multipath channel, 8PSK, SIR=-4 dB)
综合图5、图6和图7的仿真结果可知:本文提出的接收机工作在AWGN信道或多径信道情况下,当信号调制方式为QPSK或8PSK时,采用软符号重构迭代ICI干扰补偿方法的BER明显低于硬判决迭代ICI干扰补偿方法的BER。即,相对于硬判决法,软符号重构法可显著改善链路传输可靠性。另外,软符号重构法收敛速度快,仅需要一次迭代补偿就可获得满意的效果。
3 结 论
为了抑制脉冲熄灭法产生的ICI干扰,提高OFDM接收机的链路可靠性,提出了基于软符号重构的迭代ICI扰补偿方法。软符号重构迭代ICI干扰补偿方法。首先,利用译码器输出的码字比特软信息计算发送符号的软估计值;然后,利用信道衰落系数和发送符号软估计值计算得到OFDM发送信号波形;最后,根据被熄灭样值的位置信息补偿被熄灭的样值,从而消除脉冲熄灭导致的ICI干扰。随着迭代次数的增加,译码器输出码字比特软信息的精度提高,发送符号的软估计值越接近发送符号的真值,最后计算得到的发送OFDM信号的波形越精确,ICI干扰补偿后残留干扰越小,系统链路传输可靠性进一步提高。
软符号重构法优于硬判决迭代ICI干扰补偿方法,并且软符号重构迭代ICI干扰抑制方法收敛速度快,仅需1次迭代就可有效消除ICI干扰,获得满意的链路差错性能。
[1] SCHNELL M, EPPLE U, SHUTIN D, et al. L-DACS: future aeronautical communications for air traffic management[J]. IEEE Communications Magazine, 2014,52(5):104-110.
[2] JAIN R, TEMPLIN F, YIN K S. Analysis of L-band digital aeronautical communication systems: L-DACS1 and L-DACS2[C]∥Proc.of the IEEE Aerospace Conference, 2011: 1-10.
[3] NEJI N, LACERDA R D, AZOULAY A, et al. Survey on the future aeronautical communication system and its development for continental communications[J]. IEEE Trans. on Vehicular Technology, 2013, 62(1):182-191.
[4] EPPLE U, SCHNELL M. Overview of legacy systems in L-band and its influence on the future aeronautical communication system LDACS1[J].IEEE Aerospace and Electronic Systems Magazine, 2014, 29(2): 31-37.
[5] EPPLE U, HOFFMANN F, SCHNELL M. Modeling DME interference impact on LDACS1[C]∥Proc.of the Integrated Communications, Navigation and Surveillance Conference, 2012: G7-1-G7-13.
[6] BRANDES S, SCHNELL M. Interference mitigation for the future aeronautical L-band communication system[C]∥Proc.of the 7th International Workshop on Multi-carrier Systems & Solutions, 2009: 375-384.
[7] EPPLE U, SCHNELL M. Overview of interference situation and mitigation techniques for L-DACS1[C]∥Proc.of the IEEE/AIAA 30th Digital Avionics Systems Conference,2011:4C5-1-4C5-12.
[8] EPPLE U, SHUTIN D, SCHNELL M. Mitigation of impulsive frequency-selective interference in OFDM based systems[J]. Wireless Communications Letters, 2012, 1(5):484-487.
[9] LI Q Y, ZHANG J, XIE J D, et al. Iterative interference mitigation and channel estimation for L-DACS1[C]∥Proc.of the IEEE/AIAA 33rd Digital Avionics Systems Conference, 2014:3B2-1-3B2-11.
[10] LIU H T, CONG W, WANG L, et al. Symbol error rate performance of nonlinear OFDM receiver with peak value threshhold over frequency selective fading channel[J]. International Journal of Electronics and Communications,2017,74:163-170.
[11] 刘海涛,张智美,张学军.联合压缩感知与干扰白化的脉冲干扰抑制方法[J].北京航空航天大学学报,2015,41(8):1367-1373.
LIU H T, ZHANG Z M, ZHANG X J, Impulse interference mitigation method based on joint compressed sensing and whitening of interference[J]. Journal of Beijing University of Aeronautics and Astronautics, 2015, 41(8):1367-1373.
[12] LI D Z, WU Z J, DME interference mitigation for L-DACS1 based on system identification and sparse representation[J]. Chinese Journal of Aeronautics, 2016, 29(6): 1762-1773.
[13] 刘海涛,刘亚洲,张学军.联合正交投影与盲波束形成的干扰抑制方法[J].系统工程与电子技术,2015,37(8):1880-1886.
LIU H T, LIU Y Z, ZHANG X J. Interference mitigation method based on subspace projection and blind adaptive beamforming[J].Systems Engineering and Electronics,2015,37(8):1880-1886.
[14] 刘海涛,刘亚洲,张学军. 联合DOA估计与主波束形成的干扰抑制方法[J].哈尔滨工业大学学报,2016, 48(11):103-108.
LIU H T, LIU Y Z, ZHANG X J. Interference mitigation method based on joint DOA estimation and main beam forming[J]. Journal of Harbin Institute of Technology,2016,48(11):103-108.
[15] SAJATOVIC M, HAINDL B, EHAMMER M, et al. L-DACS1 system definition proposal[M]. Eurocontrol Headquarters, 2009.
[16] EPPLE U, SCHNELL M. Adaptive threshold optimization for a blanking nonlinearity in OFDM receivers[C]∥Proc.of the IEEE Global Telecommunications Conference,2012:3361-3666.
[17] BRANDES S, EPPLE U, SCHNELL M. Compensation of the impact of interference mitigation by pulse blanking in OFDM systems[C]∥Proc.of the IEEE Global Telecommunications Conference, 2009: 1-6.
[18] BRINK S, SPEIDEL J, HAN R H. Iterative demapping for QPSK modulation[J].Electronics Letters, 1998, 34(15): 1459-1460.
[19] TOSATO F, BISAGLIA P. Simplified soft-output demapper for binary interleaved COFDM with application to HIPERLAN/2[C]∥Proc.of the IEEE International Conference on Communications, 2002:664-668.
