基于Holon组织的有人/无人机作战联盟形成
2018-01-15韩博文姚佩阳
韩博文, 姚佩阳
(空军工程大学信息与导航学院, 陕西 西安 710077)
0 引 言
无人作战系统的成功应用,使未来有人/无人机集群作战成为一种趋势。从陆地的战斗机器人到海上的无人水面艇,再到空中的无人机,都已成功应用于现代作战行动中。无人机作为空中的无人作战平台,被广泛应用于空中突袭作战任务,具有长航时、高机动性、低成本等优势。然而,由于单架无人机作战能力载荷有限,面对日趋复杂的战场环境,对战场中目标群进行打击需要大量无人机平台协同完成,可见,传统的单无人机作战方式正向有人/无人机群协同作战的方式[1]发展。
在作战行动中,如何根据任务进行作战决策是影响作战效果的关键。有人战机与多架无人机组成小的作战编队联盟可以同时发挥两者优势,提高整体作战效能。文献[2]采用扩展合同网算法对有人/无人作战智能体分布式协同目标分配问题进行了研究。文献[3]将无人机作战能力分为目标信息获取能力与导弹攻击能力,研究了多机对地目标分配问题。文献[4]对防空领域“目标-火力节点-制导节点”一体的拦截联盟形成方法进行了研究。文献[5]提出了一种未知环境下异构多无人机协同搜索打击中的联盟组建方法,研究了实时性较高且适应于未知环境下的任务分配机制。
联盟是为完成某个共同任务而结合在一起的多个个体。现有联盟形成的解决方法主要集中于基于多智能体系统[6-8]与进化算法、群智能算法[9-10]的联盟形成技术。Holon系统[11]作为一种复杂自适应系统,在制造控制领域已有相关研究,但用于协同作战的研究很少。随着无人机智能化的不断提高,将面临更加复杂、动态的战场环境,现有任务分配模型多考虑编队层面的目标分配,越来越难以适应机群作战的需求。
目前,关于无人机任务分配的研究缺乏对有人/无人机群协同作战方面的研究,面对无人机群自主作战发展趋势,本文考虑实际作战需要,以有人/无人机群协同作战为背景,采用Holon联盟形成理论分析机群作战情形下的任务分配,构建有人/无人机群Holon联盟(Holon coalition of manned/unmanned vehicle swarm, HCVS)生成模型,并提出一种多目标混合蜂群(multi-objective hybrid bee colony, MHBC)算法对模型求解,验证了模型的合理性与算法的有效性。
1 HCVS数学描述
1.1 有人/无人机Holon组织
基于Holon理论的有人/无人机作战组织构建,将单机看成一个Holon单元,确定机群Holon内各Holon单元及其相互关系,以提高指挥控制系统敏捷性,从而更好地适应复杂多变的战场环境。
1.2 机群Holon联盟
有人/无人机机群Holon对目标群的作战场景中,机群面临一系列复杂任务集合,任务具有复杂性、动态性与相关性,机群Holon整体作战效能与各有人/无人机所分任务情况直接相关。
在实际作战中,面对大规模目标群的作战情况,若直接进行机群Holon到目标群的任务分配,由于任务数量较多,难以达到较好效果。为更好地进行任务分配,可将目标群中所有目标按照一定的规则进行分群,构建各目标群对应的任务集合,从而可以更快速高效地确定各目标群的资源能力需求。根据资源能力需求关系从我方机群中选出一定数量的有人/无人机Holon,并确定单机Holon与每一个目标群的最佳分配关系,形成各个编队Holon,即编队Holon联盟,编队Holon共同构成机群Holon联盟。每一个目标群所属任务集合内的所有任务即为对应编队联盟的任务,所有编队联盟共同完成机群Holon整体任务。因此,有人/无人机群对目标群的打击效果取决于面向各目标群的编队联盟力量编成方案的优劣。
1.3 HCVS任务分解
机群对目标群Ta的作战总任务为对所有目标进行打击构成的任务集合,记为T,表示为
T={t1,t2,…,ti,…,tN}
(1)
式中,ti为对目标Tai的打击任务;N为目标的数量。
分解HCVS作战总任务应依据各有人/无人机Holon单元的能力,以单个Holon所能完成的最小任务为基本任务单元,将HCVS作战总任务分解为一系列可由单个Holon完成的子任务。
基于联盟机制的作战,可将对目标进行侦察跟踪、火力攻击、毁伤评估的任务分配给不同平台来执行,从而可将任务ti进一步分解为
(2)

如图1所示,机群对多目标群的作战总任务T可分解为

(3)

图1 目标任务分解Fig.1 Task decomposition of targets
HCVS形成问题,就是将总任务T进行分组T1={t1,t2,…,tNT1},T2={t1,t2,…,tNT2},…,TNA={t1,t2,…,tNTNA},并为每一任务分组生成相应的有人/无人机编队联盟A1={V1,V2,…,VNV1},A2={V1,V2, …,VNV2},…,ANA={V1,V2,…,VNVNA}。其中,NA为任务分组的数量,即编队联盟数量,NTk为任务分组Tk内的目标数量,NVk为完成任务分组Tk所形成的编队联盟内的无人机数量,k∈[1,NA],且T={T1,T2,…,TNA}。因此,单个联盟任务可以分解为

(4)

1.4 HCVS形成问题设计
假设我方有人/无人机分布于多个基地Ba={Ba1,Ba2,…,Bai,…,BaNBa},其中,NBa为基地数量,各基地均配备一定数量的有人/无人机。有人机集合为V={V1,V2,…,VNV},其中,NV为有人机数量。各基地内无人机Holon集合为H1={h1,h2,…,hN1},H2={h1,h2,…,hN2},…,HNBa={h1,h2,…,hNNBa},N1,N2,…,NNNBa为各基地内无人机Holon数量,单机Holon总数量为NH=N1+N2+…+NNNBa。目标群集合为Ta={Ta1,Ta2,…,Tai,…,TaN},各目标群都包含一定数量已知目标。
在任务分解的基础上,HCVS可描述如下:



2 HCVS形成方案优化模型
HCVS形成问题,就是为任务组T1,T2,…,TNA形成NA个编队联盟,在满足任务需求的前提下使联盟力量编成方案效果最优。
为了准确描述HCVS形成问题模型,先对问题作如下假设。
假设1假设HCVS形成过程中,只考虑有人/无人机平台资源能力对HCVS形成的影响,而忽略其他因素的影响。
假设2假设HCVS形成过程是在非超加性环境中进行的。超加性是指对于任意两个编队联盟A1,A2,且A1∩A2=∅,有BA1+A2≥BA1+BA2,BA为编队联盟资源能力,在非超加性环境中包含所有战机的最大联盟是最有益的。
HCVS力量编成中还包括有人机对无人机的指挥控制关系,确定各编队联盟内无人机与有人机的指挥控制关系,就是根据各目标群的任务需求,为每一个编队分派具备指挥决策能力的有人机,以完善编队力量编成方案,如图2所示。

图2 有人/无人机指挥控制关系Fig.2 Control and command relationship between mannedaerial vehicle and unmanned aerial vehicles
同时,HCVS力量编成过程中,在满足任务需求前提下,有人机数量过多会使人员伤亡的可能性增大,有人机数量过少会使其在指挥无人机作战的过程承受过多负载;同样,无人机数量过多,会造成不必要的资源能力冗余,不符合信息化作战快速、高效的基本要求。
较好的有人/无人机编队联盟力量编成方案可以高效优化机群整体的资源能力,使其在满足作战任务需求的前提下减少并均衡负载,同时为应对作战过程中的突发情况(包括无人机损毁、发现新的目标等),应保持一定资源能力冗余,提高HCVS的整体作战效能,快速、高效地达到我方打击敌目标群的作战目标。
下文先给出HCVS力量编成资源冗余的测度方式,然后建立HCVS形成问题优化模型。
2.1 资源冗余
机群资源的有效分配可以提高整体作战效能。单个编队联盟Ak执行联盟任务Tk的资源冗余定义为
(5)

2.2 多目标优化模型
由第2节前述的分析可知,在预留一定资源能力冗余的前提下,HCVS资源分配越均衡、高效,HCVS整体作战效能越高,越有利于我方军事行动。因此评估HCVS力量编成方案优劣的目标函数可从以下两方面考虑:
(1) 使HCVS中所有编队的平均资源能力冗余η最小,即
(6)
式中,NA为编队联盟数量;ηk为编队联盟Ak的资源能力冗余。
(2)使HCVS中资源能力冗余的方差Dη最小,即

(7)
HCVS形成问题的约束如下。
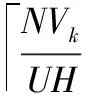

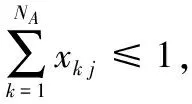
约束4单个编队联盟Ak所具备的资源能力BAk必须满足编队任务Tk的资源能力需求DTk,即

(8)

综上所述,HCVS形成问题的多目标优化模型为
(9)
式中,f为模型目标向量;模型的决策变量为指挥控制决策变量MH-V=(mij)与编队决策变量XH-A=(xkj)。
3 基于MHBC算法的联盟生成
人工蜂群算法是于2005年提出的一种新型群智能算法[11],求解优化问题具有很大优越性。文献[12]提出了混合蜂群算法(hybrid bee colony,HBC),提高了算法搜索性能与精度。本文采用多目标优化问题处理方式在其基础上提出一种多目标混合蜂群(multi-objective hybrid bee colony,MHBC)算法求解式(9)中的优化模型。
3.1 蜜源编、解码
在MHBC算法中,蜜源位置表示为R=(r1,r2,…,rNH),其中,ri为实数,满足约束ri∈(0,NA+1)。每一处蜜源位置经过解码后,对应模型的一个解。蜜源解码步骤如下:
步骤1将实数位置向量映射为位置矩阵XH-A=(xkj),满足
(10)
并且映射后满足第2.2节中约束2。映射变换方法为:实数位置向量小数部分的排序代表无人机编号,整数部分代表编队联盟编号,整数部分相同则表示属于同一个编队联盟。如图3所示,以6架无人机形成2个编队联盟为例,蜜源位置向量为6维实数向量,整数部分代表编队联盟编号,小数部分以升序进行排序后对应无人机编号。
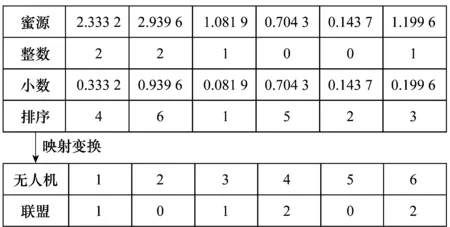
图3 蜜源位置与决策矩阵的映射变换关系Fig.3 Mapping relationship between the nectar source position and the decision matrix
步骤2列检查。按照约束2对各列进行检查。如果该列中元素1多于一个,则随机选择一个1置为零。
步骤3行检查。按照约束3对各行进行检查。如果该行不满足式(8),则从所有列中选取一个元素全为0的列,将所选列中所属该行的0置为1,计算是否满足式(8),若仍不满足,则继续该操作;若矩阵中不存在元素全为0的列,则从该行随机选取一个0置为1,所在列其余元素全置为0。
根据蜜源解码后得到的位置矩阵可以计算优化模型的目标函数f=(η,Dη),作为蜜源位置的适应度函数,其值将随着蜜源位置的更新而更新。令蜜源X1的适应度值为f1,X2的适应度值为f2,若f1支配f2,则蜜源X1优于X2;若f2支配f1,则蜜源X1劣于X2;若f1与f2互不支配,则X1非优非劣于X2。
3.2 非劣解档案维护
MHBC算法为每只蜜蜂建立相应的个体档案,保存该蜜蜂寻找蜜源过程中的最优蜜源位置,并为蜂群整体维持一个整体档案,保存蜂群整体所经历的最优蜜源位置。维护蜜蜂个体档案的规则为:当某只蜜蜂发现新蜜源时,若新蜜源优于该蜜蜂档案内的当前蜜源,则将该蜜蜂档案当前蜜源更新为此新蜜源;若新蜜源劣于该蜜蜂档案内的当前蜜源,则不更新;若新蜜源非优非劣于该蜜蜂档案内的当前蜜源,则随机决定是否进行更新。维护整体档案的规则为:当蜂群发现新蜜源时,采取非支配排序法对整体档案进行更新,且整体档案容量为GW。
3.3 蜜源更新
采蜜蜂在其蜜源周围,按照式(11)寻找优质蜜源,并将其存入档案。

(11)

跟随蜂依照轮盘赌策略选择采蜜蜂,并在其蜜源位置附近按照式(11)重新搜索蜜源,更新个体档案。
侦察蜂按照式(12)选取新的食物源,更新个体档案。
vk,j=xk,j(1+(2rand[0,1]-1)·

(12)
式中,参数dmax,dmin,a,b取常数;xk,j表示侦察蜂搜索前位置;vk,j表示侦察蜂搜索后新位置;k的取值范围为侦察蜂的数量;cycle为迭代次数;Cyclemax为迭代次数的上限。
3.4 算法流程
MHBC算法流程如图4所示。
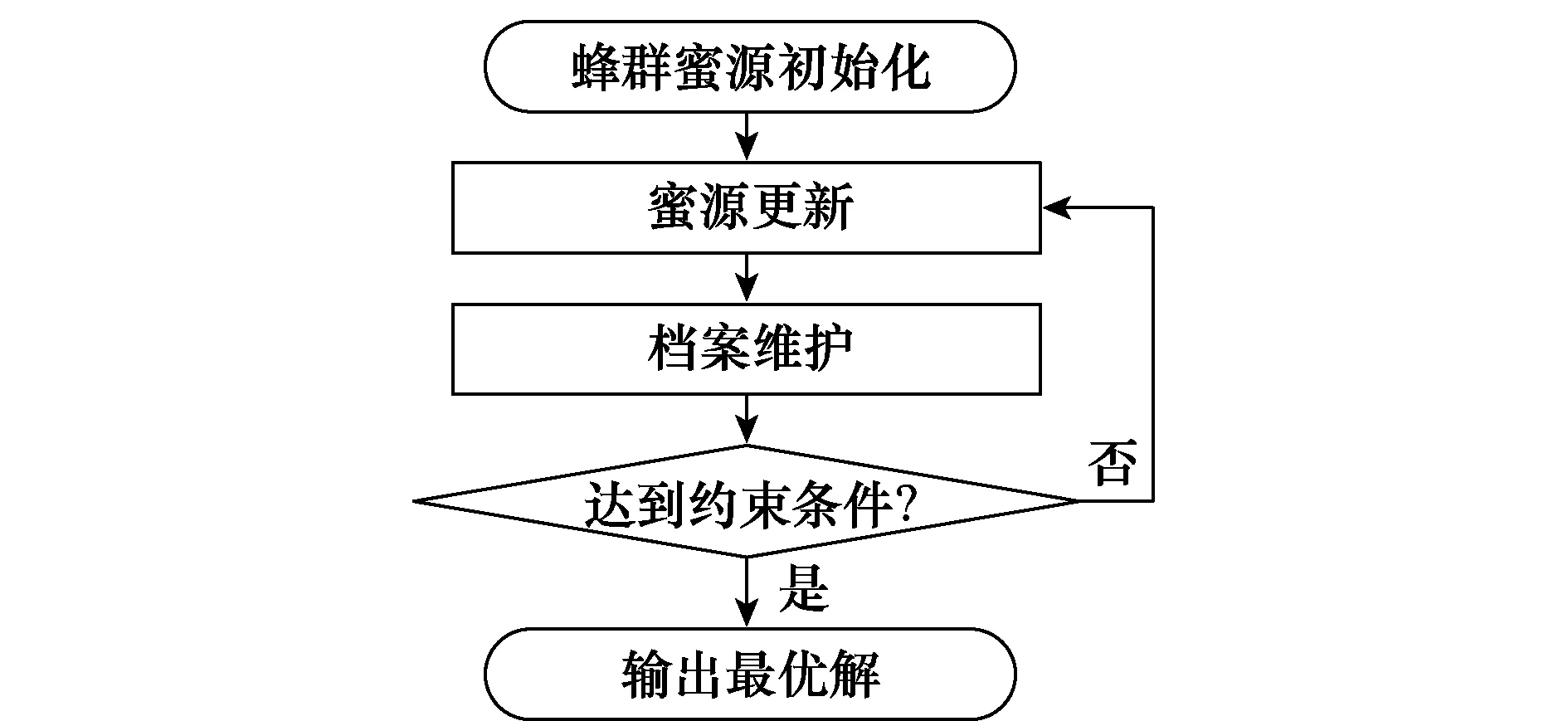
图4 MHBC算法具体流程Fig.4 MHBC algorithm specific process
4 实验结果及分析
本文设计了两个仿真实验,一是验证提出的MHBC算法对多目标优化问题的求解性能;二是验证编、解码处理后MHBC算法求解HCVS形成问题的有效性。仿真实验均在Intel(R) Core(TM) i3-4150 CPU 3.50 GHz计算机上。
仿真实验1已知我方有4个无人机基地,各基地分别有多架类型与资源能力不同的有人机V={V1,V2,…,VNV}、无人机H={H1,H2,…,HNBa},如表1所示,资源能力向量前三维、后三维分别代表侦察、评估资源能力,中间两维代表火力攻击资源能力。现有4个目标群,每个联盟任务的资源需求如表2所示。根据作战使命要对各目标群内所有目标实施打击。本文提出的MHBC算法具有人工蜂群算法的局部搜索性能与模拟退火算法的全局搜索性能,分别采用MHBC算法与第2代非支配排序遗传算法(non-dominated sorting genetic algorithm -Ⅱ, NSGA-Ⅱ)进行求解,从两种方法所得Pareto解集合中各随机选取一个解,解码后所得方案如表3所示。

表1 有人/无人机资源能力

表2 联盟任务资源能力需求

表3 联盟形成方案
从所得方案可以看出,在平均资源冗余指标方面,MHBC算法所得方案与NSGA-Ⅱ算法所得方案基本相同,在资源冗余方差指标方面,MHBC算法所得方案却比NSGA-Ⅱ算法所得方案小很多,由于机群作战资源较多且分配情况复杂,为应对意外情况,应预留一定资源能力冗余,故MHBC算法所得方案优于NSGA-Ⅱ算法所得方案。
仿真实验2为衡量MHBC算法的性能,可选取常用于求解多目标优化问题的NSGA-Ⅱ[13],将两方法求解情况进行对比。评价多目标算法性能的指标主要包含收敛性、覆盖性、均匀性与算法耗时[14]。分别使用本文MHBC算法和NSGA-Ⅱ算法求解仿真案例,设置算法迭代次数上限为100,种群初始规模为60,两算法分别运行30次,各指标结果如图5所示。
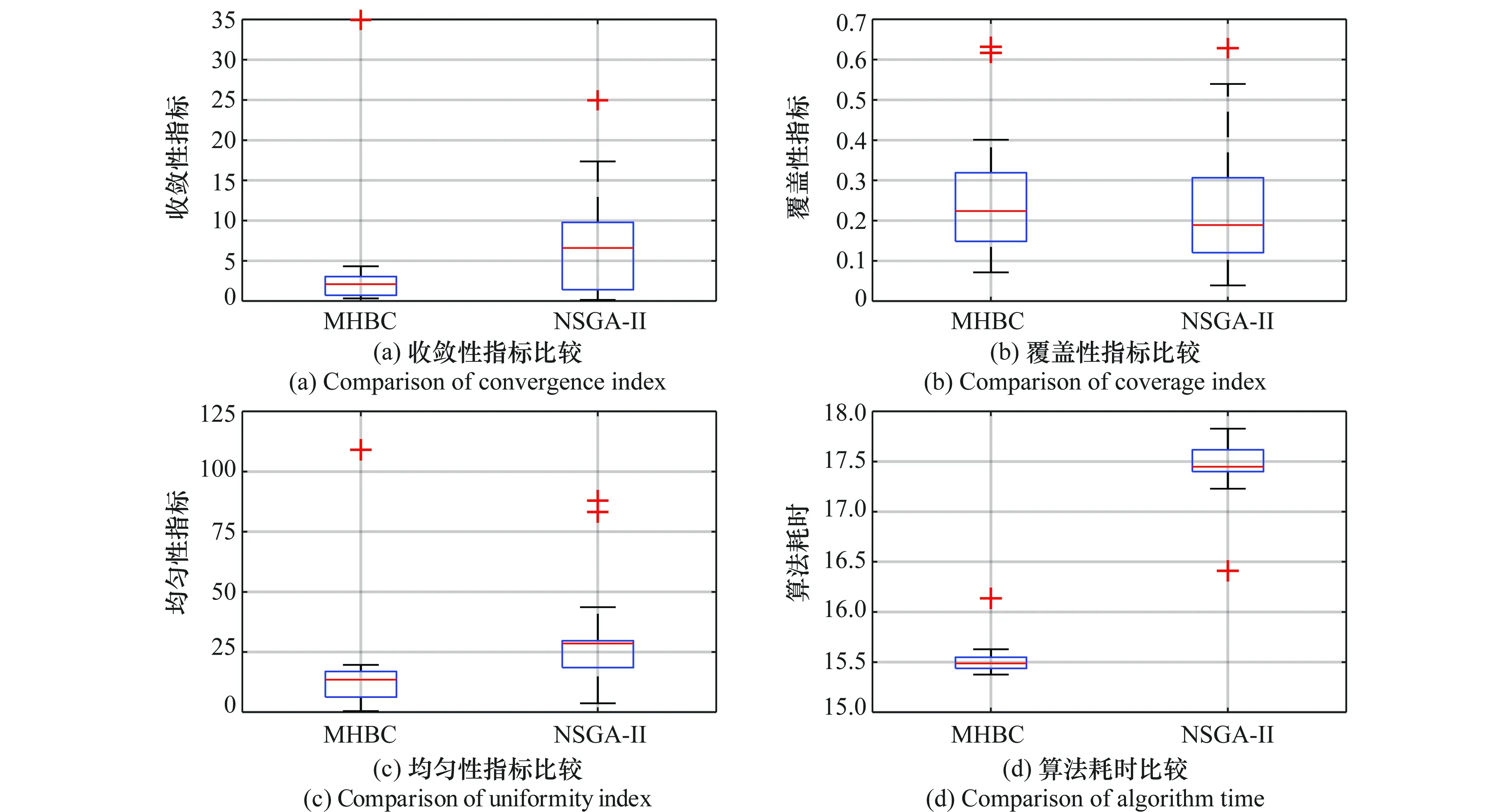
图5 算法比较Fig.5 Comparison of algorithms
由于收敛性、均匀性与算法耗时3种指标值越小,覆盖性指标值越大,算法性能越好,由图5可知,MHBC算法在解集的覆盖性上与NSGA-Ⅱ算法相差不大,然而收敛性、均匀性均优于NSGA-Ⅱ算法,并且耗时更短,在实际作战中具有重要意义,因此本文所设计的MHBC算法在求解HCVS形成问题时有更好的效果。
5 结束语
对HCVS形成问题进行了研究,首先,对HCVS形成问题进行了数学描述;其次,为生成最好的HCVS力量编成方案,以均衡和最小化HCVS的资源冗余为目标函数建立了HCVS形成模型,设计了MHBC模型求解算法;最后,通过仿真实验证明了所设计模型与算法的合理性、有效性。不足之处在于,建立模型时未考虑任务的执行时间与执行情况,而在实际作战中,难免出发突发情况,任务的执行未必完全按照预期计划进行。因此,下一步工作将对所建立的模型进行完善,研究不确定性环境下有人/无人机群作战联盟演化方法。
[1] HEADQUARTERS. United States air force unmanned aircraft systems flight plan 2009-2047[R]. Washington DC: United States Air Force, 2009.
[2] 万路军,姚佩阳,周翔翔,等.有人/无人作战智能体分布式协同目标分配方法[J].系统工程与电子技术,2014,36(2):278-287.
WAN L J, YAO P Y, ZHOU X X, et al. Distributed cooperative target assignment method of manned combat agents and unmanned combat agents[J]. Systems Engineering and Electronics, 2014, 36(2): 278-287.
[3] 王强,丁全心,张安,等.多机协同对地攻击目标分配算法[J].系统工程与电子技术,2012,34(7):1400-1405.
WANG Q, DING Q X, ZHANG A, et al. Target allocation algorithm for multi-cooperative air-to-ground attack[J]. Systems Engineering and Electronics, 2012, 34(7): 1400-1405.
[4] 唐苏妍,朱一凡,葛伟,等.网络化防空导弹体系集中式拦截联盟形成方法[J].系统工程理论与实践,2011,31(2):357-363.
TANG S Y, ZHU Y F, GE W, et al. Centralized interception coalition formation method in network worked air defense missile systems[J].System Engineering Theory & Practice,2011,31(2): 357-363.
[5] BREBAN S, VASSILEVA J. A coalition formation mechanism based on inter-Agent trust relationships[C]∥Proc.of the International Conference on Autonomous Agents, 2002: 306-307.
[6] GONG Y, YAO L, ZHANG W M. Research of coalition formation in time bounded multi-agent systems[C]∥Proc.of the International Conference on Machine Learning and Cybernetics, 2002: 194-198.
[7] SERVICE T C, ADAMS J A. Coalition formation for task allocation: theory and algorithms[J]. Autonomous Agents and Multi-agent Systems, 2011, 22(2): 225-248.
[8] 蒋建国,张国富,齐美彬,等.基于离散粒子群求解复杂联盟的并行生成[J].电子与信息学报,2009,31(3):519-522.
JIANG J G, ZHANG G F, QI M B, et al. Complicated coalition parallel generation based on discrete particle swarm optimization[J]. Journal of Electronics & Information Technology, 2009, 31(3): 519-522.
[9] KIAM T S, KWANG M S, SHANG Y C K. Coalition formation for resource collocation using BDI assignment agents[J]. IEEE Trans.on Systems, Man, and Cybernetics-Part C: Applications and Reviews, 2007, 37(4): 682-693.
[10] YU F, TU F, PATTIPATI K R. Integration of a holonic organizational control architecture and multi-objective evolutionary algorithm for flexible distributed scheduling[J]. IEEE Trans.on Systems,Man,and Cybernetics-Part A:Systems and Humans, 2008, 38(5): 1001-1017.
[11] KARABOGA D. An idea based on honey bee swarm for numerical optimization[R]. Turkey: Erciyes University, Engineering Faculty, Computer Engineering Department, 2005.
[12] 王慧颖, 王文彬. 基于改进搜索策略的混合蜂群算法[J]. 系统工程与电子技术, 2014, 36(10): 2094-2101.
WANG H Y, WANG W B. Hybrid bee colony algorithm with modified search strategy[J]. Systems Engineering and Electronics, 2014, 36(10): 2094-2101.
[13] DEB K, PRATAP A, AGARWAL S, et al. A fast and elitist multi-objective genetic algorithm: NSGA-Ⅱ[J]. IEEE Trans.on Evolutionary Computation, 2002, 6(2): 182-197.
[14] VAN V D A, LAMONT G B. On measuring multi-objective evolutionary algorithm performance[C]∥Proc.of the Congress on Evolutionary Computation, 2009: 204-211.
