严格回归轨道的管道导航方法研究

，，，

1. 上海航天控制技术研究所，上海 201109 2. 上海市空间智能控制技术重点实验室，上海 201109

近地遥感卫星常利用星载SAR相位差分干涉成像，为获得高质量的成像效果，需要实现高精度的星下点定时重访。国外多个卫星项目提出了严格回归轨道和卫星管道保持的概念。譬如，德国的ERS卫星实现管径300 m[1-2]、TerraSAR-X实现管径250 m[3-4]，日本的ALOS实现管径500 m[5]。严格回归轨道具有高精度的空间轨迹重访能力，管道保持以严格回归轨道为参考轨道，要求卫星的运行轨迹保持在参考轨道附近的管道内。相较早期的轨迹保持技术[6-7]，管道保持实现的空间轨迹重访要求更为严格，具有空间和时间的双重约束。本文基于高精度轨道动力学确定的严格回归轨道，将近地遥感卫星与参考轨道采样点视为一个虚拟编队，以虚拟编队相对运动特性作为导航分析的对象[8]。管道导航的目的是提炼出近地遥感卫星与参考轨道采样点之间相对运动的特征量，进而参考编队控制策略来实现虚拟编队的管道保持。区别于传统的基于测控的轨道控制，卫星按预设的参考轨道运行具有某种意义上的智能自主控制特性，属于未来卫星应用领域的一个重要发展趋势[9]。

管道导航的问题在于，参考轨道的设计只考虑地球非球形摄动，与在轨卫星的动力学环境存在差别，导致近地遥感卫星与参考轨道采样点之间存在切航向和径向的漂移[10-11]。由于严格回归轨道设计的参考轨道的星下点轨迹包含了时间因素，切航向漂移造成的相位时间偏差会影响对地观测任务，必须予以补偿；径向漂移则会加剧切航向漂移的积累。为此，需要获取近地遥感卫星和参考轨道采样点的相位时间偏差和相对运动轨迹特征量，才能借鉴已有的卫星编队控制方法[12-13]。

本文基于高精度轨道动力学模型和位置确定方法，提出了一种近地遥感卫星与参考轨道采样点的沿航向对齐算法，获取了近地遥感卫星与参考轨道采样点的相位时间偏差、相对运动轨迹。进而由数据拟合方法获取了相对运动轨迹的特征量，作为管道导航的结果。

1 管道导航概述

1.1 卫星与参考轨道采样点的相对运动特性

由于大气阻力的作用，近地遥感卫星在轨运行时，其轨道半长轴相比参考轨道存在衰减，其相位会逐渐超前于参考轨道采样点，这是严格回归轨道需要进行管道控制的根本原因。遥感卫星与参考轨道采样点具有两种相对运动状态：

1) 对于初始状态完全一致的近地遥感卫星与参考轨道采样点、完成轨道保持超调控制后一段时期内，卫星的相位会滞后于参考轨道采样点；

2) 随着近地遥感卫星轨道高度的降低，其轨道角速度增大，卫星的相位会逐渐超前于参考轨道采样点。

1.2 管道导航的任务需求

管道保持的目标是使近地遥感卫星的空间轨迹与参考轨道保持一致，管道导航的任务是获取近地遥感卫星相对参考轨道的相位时间偏差和相对运动轨迹的特征量。

在分析由相位时间偏差造成的轨迹漂移时，需要考虑轨道的进动与地球的自转。卫星升交点赤经变化率在轨道一周内的平均值为:

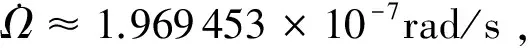
由相位时间偏差引起的轨迹漂移

根据式(2)，0.7 s的相位时间偏差导致的轨迹漂移约330 m，该量级的相位时间偏差是轨迹漂移突破管径约束的重要因素。

2 管道导航方法

2.1 编队坐标系

编队坐标系定义为以参考轨道采样点为原点O，径向OXH轴沿地心E至O的矢量方向，切航向OYH轴在参考轨道平面内垂直OXH指向飞行方向为正，法向OZH轴由右手法则确定，如图1所示。

2.2 坐标系转换

由惯性系到编队坐标系的位置变量满足转换关系[14-15]

式中：XH为卫星在编队坐标系下的坐标；ΔXJ2000为卫星与参考轨道采样点在J2000坐标系中的位置偏差；Abo为轨道坐标系到编队坐标系的转换矩阵;Aoi为惯性系到轨道坐标系的转换矩阵。

根据莱布尼茨公式，由惯性系到编队坐标系的速度变量满足转换关系:

2.3 基于参考轨道的沿航向对齐

(1)沿航向对齐的基本原理

沿航向对齐算法基于轨道动力学模型与位置确定方法，其实质是通过数值迭代逼近方法，得到近地遥感卫星与参考轨道采样点的相位时间偏差和相对运动轨迹。

以卫星的相位超前于参考轨道采样点的情况为例，对沿航向对齐算法原理进行说明。如图2所示，该情况下需要选择近地遥感卫星合适的前序运动状态作为算法输入，通过轨道递推结合运动状态的迭代更新来实现沿航向对齐。

(2)基于分层迭代的沿航向对齐算法

基于分层迭代的沿航向对齐算法通过对时间轴N等分并遍历的方式来实现算法功能，计算量大,实时性差。算法流程如下：

1)设置ti时刻参考轨道采样点的惯性系位置rm(ti)为编队坐标系原点，以前序时刻ti-j的惯性系位置rf(ti-j)、速度vf(ti-j)为初始状态，进行步长h1=(ti-ti-j)/N的轨道递推。

3)进行迭代算法中下一层的轨道递推，以满足沿航向对齐判据的时刻以rf(tk)和vf(tk)为起始状态，进行步长h2=h1/N的轨道递推。

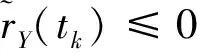
(3) 基于二分法的沿航向对齐算法

基于二分法的沿航向对齐算法，通过对时间轴二等分并缩小时间区间的方式来实现算法功能，类似数学分析中“闭区间套定理”，计算量小,实时性好。算法流程如下：

基于分层迭代和基于二分法的沿航向对齐算法比照如图3所示。

(4) 简化的轨道递推模型

轨道递推通常采用高阶次、高精度的重力势场模型。星上管道导航算法进行小积分步长的轨道递推时，可以考虑采用低阶次的重力势场模型。通常情况下，4×4阶次的截断系数即可满足短时间内轨道递推的精度要求，且计算资源要求较小。

2.4 相对运动轨迹的特征量获取

近地遥感卫星在编队坐标系XHOZH平面内的相对运动轨迹为一个偏置的倾斜椭圆，如图4所示。其中(xc,yc)表示编队坐标系下偏置倾斜椭圆的中心坐标；aFF表示半长轴长；bFF表示半短轴长；ξFF表示椭圆半长轴与ZH夹角，取值ξFF∈[-π/2,π/2]。

经沿航向对齐算法，可以获取近地遥感卫星在参考轨道编队坐标系下的位置、速度。取一个轨道周期的N个采样点{(xHi,zHi)|i=1,2,…,N}，利用数值拟合方法获取椭圆的一般方程：

记α=[a,b,c,d,e,f]T，z=[x2,xy,y2,x,y,1]T，椭圆的拟合问题等价于

findα=[a,b,c,d,e,f]

[16-17]中，介绍了一种椭圆“最小二乘适配法”，该方法将数值拟合问题转化为对矩阵特征值及特征向量的求解。

定义分布矩阵S：

在求解α=[a,b,c,d,e,f]T的基础上，通过待定系数法求解偏置倾斜椭圆的特征量(xc,yc)，aFF>0，bFF>0，ξFF。

假设XHOZH平面内倾斜椭圆绕面外的YH轴旋转至水平位置，记η=-ξFF。经过旋转后，椭圆一般方程x2,xy,y2,x,y和常数项的系数分别为：

依据水平椭圆的混合项系数为零，可得到

依据待定系数法，椭圆特征量满足：

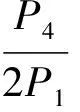
3 数值试验

3.1 管道导航的仿真条件

高精度轨道动力学模型采用90×90阶次的EGM2008重力势场；近地遥感卫星的质量设置为2 900 kg，迎风面积取7.6 m2，面质比约为0.002 6 m2/kg；大气阻力采用Jacchia1971模型，Cd取值2.2；太阳光压的反射系数Cr取值0.8。

参考轨道如表1所示，设置近地遥感卫星和参考轨道的初始运动状态设置完全一致。起始历元2015年10月1日0时0分0秒，仿真步长取1 s。参考轨道动力学的摄动项只含高阶次的地球重力势场；近地遥感卫星的动力学包含全类摄动。

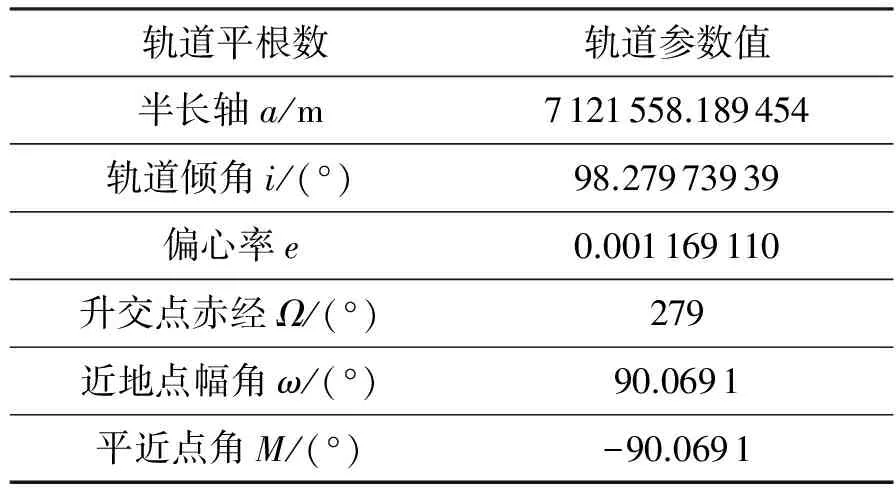
表1 初始轨道平根数[18]Table 1 Initial mean orbit elements[18]

3.2 管道导航的动力学基准

管道导航的动力学基准为不加导航测量误差的轨道信息，结合90×90阶次的轨道递推和分层迭代的沿航向对齐，并进行特征量拟合得到的结果。根据上述仿真条件进行10天的轨道积分，对第7～9天的0时刻进行沿航向对齐后，获取相位时间偏差，如表2所示。可以观察到，对于初始状态完全一致的近地遥感卫星与参考轨道采样点(相位时间偏差为零)，750 km轨道经过8天左右的漂移，相位时间偏差累积到0.7 s左右。

分别对第7～9天第1轨的数据进行沿航向对齐，如图5所示。图中“∘”点为编队坐标系原点，即参考轨道采样点；未经沿航向对齐的卫星相对运动轨迹在切航向逐渐增大且不规则，经过沿航向对齐的近地遥感卫星相对运动轨迹为一个接近闭合的偏置倾斜椭圆。

表2 超前相位时间的统计Table 2 Statistics of phase-time excursions

3.3 管道导航算法的偏差分析

管道导航的偏差通过管道导航算法输出、管道导航的动力学基准进行比对得到。管道导航算法模拟了GNSS的测量误差(数据频率1 Hz，位置精度10 m)和绝对轨道导航模块；考虑到星载计算机能力约束，星载软件采用计算更加高效的4×4阶次轨道递推和二分法迭代进行沿航向对齐。管道导航偏差分析方法原理如图6所示。

对第7～9天的第1轨进行管道导航，考虑GNSS测量误差下，沿航向对齐结果与动力学基准的比对如图7所示。管道导航的偏差分析结果如表3所示。

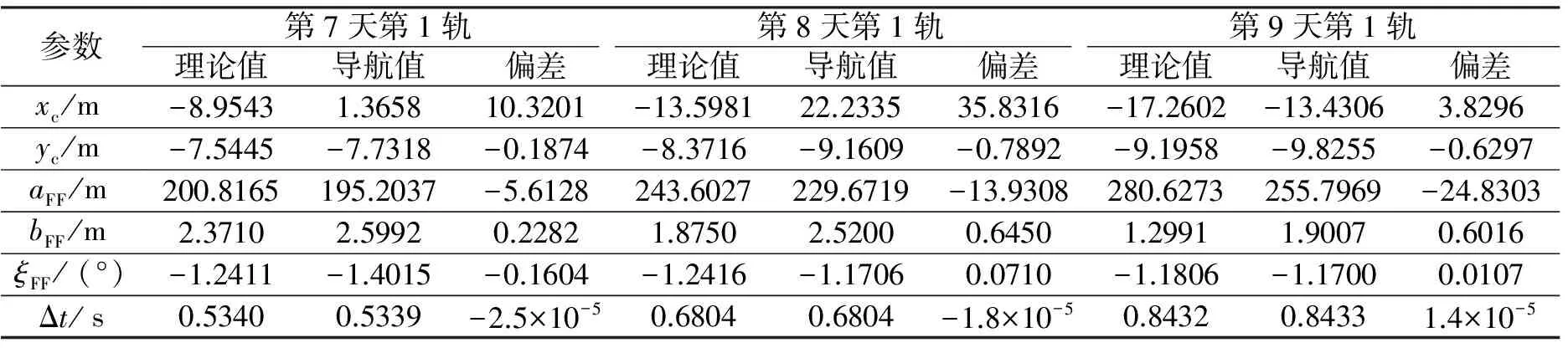
表3 管道导航的偏差分析Table 3 Precision analysis of tube-navigation

4 结束语

1)本文针对高精度空间轨迹定时重访的任务需求，提出了以严格回归轨道作为参考轨道的管道导航方法。结合虚拟编队的控制技术，能够赋予卫星自主轨道维持能力。

2)基于轨道动力学模型、高精度位置确定方法，提出了近地遥感卫星与参考轨道采样点的沿航向对齐算法，进而获取近两者的相位时间偏差。

3)在沿航向对齐的基础上，引入椭圆“最小二乘适配法”，获取了相对运动轨迹的特征量。

4)针对星载计算机的能力约束，提出了适于星载软件使用的简化轨道递推模型和基于二分法迭代的切向对齐算法，并对管道导航的偏差进行了分析。

参考文献(References)

[1] ROSENGREN M. The orbit control of ERS-1 and ERS-2 for a very accurate TANDEM configuration[J]. RBCM, Special Issue, 1999(21): 72-78.

[2] REMKO S, PIETER V, NEIL P. ERS orbit determination and gravity field model tailoring: recent developments[J]. European Space Agency, Special Publication, 2000(461): 715-725.

[3] CHRISTIAN A, SIMONE D A, EINEDER M. Precise groud-the-loop orbit control for low earth observation satellites[C]∥Proc. of the 18th International Symposium on Space Flight Dynamics, Munich, Germany, 11-15 October, 2004: 333-338.

[4] AORPIMAI M, PALMER P L. Repeat-ground track orbit acquisition and maintenance for earth-observation satellites[J]. Journal of Guidance Control and Dynamics, 2007, 30(3): 654-659.

[5] YUJI O, YUKIHIRO K, SHINICHI S. ALOS-2 development status and draft acquisition strategy[C]∥Proc. of the SPIE Sensors, Systems, and Next-Generation Satellites Conference, Edinburgh, UK, 19 November, 2012: 2288-2291.

[6] 赵坚. 太阳同步(准)回归轨道卫星的轨道保持方法研究[J]. 中国空间科学技术, 2004, 24(4):60-64.

ZHAO J. Research on the orbit keeping of sun-synchronous repeating orbit[J]. Chinese Space Science and Technology, 2004, 24(4):60-64 (in Chinese).

[7] 陈洁，汤国建. 中低轨道卫星控制方法[J]. 上海航天, 2005, 22(1): 24-30.

CHEN J, TANG G J. The method of medium lowaltitude satellite control[J]. Aerospace Shanghai, 2005, 22(1): 24-30 (in Chinese).

[8] 杨维廉. 基于轨道摄动解的卫星编队飞行[J]. 宇航学报, 2008, 29(4): 1166-1171.

YANG W L. Formation flying based on orbit perturbation solution[J]. Journal of Astronautics, 2008, 29(4): 1166-1171 (in Chinese).

[9] 吴宏鑫, 胡军, 解永春.航天器智能自主控制研究的回顾与展望[J]. 空间控制技术与应用, 2016, 42(1): 1-6.

WU H X, HU J, XIE Y C. Spacecraft intelligent autonomous control: past, present and future[J]. Aerospace Control and Application, 2016, 42(1): 1-6 (in Chinese).

[10] 温生林，闫野，张华. 低轨回归轨道卫星轨迹漂移特性分析与控制[J]. 系统工程与电子技术, 2015(3):613-619.

WEN S L, YAN Y, ZHANG H. Analysis and control of ground-track drift for recursive low earth orbit satellites[J]. Systems Engineering and Electronic, 2015(3):613-619 (in Chinese).

[11] 杨乐平，朱彦伟，黄涣. 航天器相对运动轨迹规划与控制[M]. 北京：国防工业出版社, 2010.

[12] 贺东雷，曹喜滨，马骏，等. 基于相对偏心率/倾角矢量的编队控制方法[J]. 系统工程与电子技术, 2011, 33(4): 833-837.

HE D L, CAO X B, MA J, et al. Formation control approach based on relative eccentricity/inclination vector[J]. Systems Engineering and Electronic, 2011, 33(4): 833-837 (in Chinese).

[13] 刘付成，完备，杜耀珂，等. 近地轨道编队飞行卫星构形保持控制方法研究[J]. 上海航天, 2014, 31(4): 6-10.

LIU F C, WAN B, DU Y K, et al. Research on satellites formation-keeping control in low earth orbit[J]. Aerospace Shanghai, 2014, 31(4): 6-10 (in Chinese).

[14] 杨嘉墀，范剑峰. 航天器轨道动力学与控制[M]. 北京：中国宇航出版社, 1995.

[15] 刘林. 航天器轨道理论[M]. 北京：国防工业出版社， 2000.

LIU L. Orbit theory of spacecraft[M]. Beijing: National Defense Industry Press, 2000 (in Chinese).

[16] RADIM H, FULSSER J. Numercial stable direct least squares fitting of ellipses[C]∥Proc. of the 6th International Conference in Central Europe on Computer Graphics and Visualization, Plzen-Bory,Czech Republic,9-13 February,1998: 121-128.

[17] ANDREW F, MANURIZIO P, RPBERT B F. Direct least squares fitting of ellipses[J]. IEEE Transaction on Pattern Analysis and Machine Intelligence, 1999, 21(5): 476-480.

[18] 杨盛庆，杜耀珂，陈筠力. 基于迭代修正方法的严格回归轨道设计[J]. 宇航学报, 2016, 37(4): 420-426.

YANG S Q， DU Y K，CHEN J L. Design of strictly regressive orbit based on iterative adjustment method[J]. Journal of Astronautics, 2016, 37(4): 420-426 (in Chinese).