基于高斯滤波和近似积分的电动车窗防夹算法∗

刘建国，付 恒，饶政玉，赵永浩

(1.武汉理工大学，现代汽车零部件技术湖北省重点实验室，武汉 430070； 2.汽车零部件技术湖北省协同创新中心，武汉 430070；3.武汉东环车身系统有限公司，武汉 430056； 4.吉利汽车研究院(宁波)有限公司，宁波 315000)

前言

2015年全球汽车销量达到8 290万辆，其中电动车窗的销量超过3亿件。随着电动车窗的广泛普及，由电动车窗造成的乘客(尤其是儿童)伤害事件的数量也在逐年递增。欧洲和美国分别制定了74/60/EEC和MVSS18法规[1]，法规中规定了电动车窗的正常升降要求和自动防夹要求。

汽车行驶工况较为复杂，实际中有沥青路、卵石路、比利时路和深坑路等多种路面；还有车窗胶条老化、蓄电池电压波动等情况。基于卡尔曼滤波的防夹算法[2]，通过测量值和估计值的协方差的循环迭代，对霍尔信号脉宽波形进行滤波，再将霍尔信号脉宽转换成转矩，利用转矩的变化率来判断是否达到防夹要求。该算法在车身振动幅度较大的情况下，容易产生误防夹。

为解决上述问题，本文中提出一种算法，通过高斯滤波滤除霍尔信号的一部分噪声，可有效平滑波形。滤波虽能降低尖峰噪声的幅值，但是仍容易产生误判。针对这个问题，继续采用近似积分法，即对霍尔信号脉宽波形进行积分。尖峰噪声虽然幅值很大，但积分后的面积却很小，这样即可减少误防夹的几率。相比于基于卡尔曼滤波的防夹算法，本文中提出的算法具有更小的运算量和更高的鲁棒性。

1 防夹车窗数学模型

1.1 电机转矩的状态空间模型

车窗电机一般为两相有刷直流电机，直流电机电压平衡方程[2]为

式中：ua，ub为相电压；Ra，Rb为相电阻；ia，ib为相电流；La，Lb为线圈自感；Lba，Lab为线圈互感；P 为微分算子；ea，eb为反向电动势。

根据电机结构的对称性[3]可知：

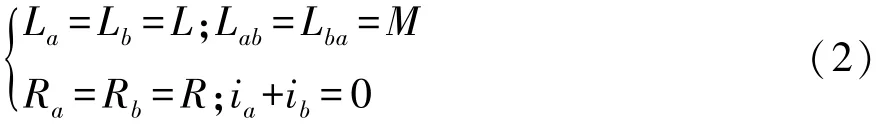
式中：L为线圈自感；M为线圈互感；R为相电阻。

因此，式(1)可改写为

式中：ωm为电机角速度；Pe为电磁功率；Te为电磁转矩。线圈运动方程[4]为

式中：B为线圈阻尼系数；Jm为电机转动惯量；TL为负载转矩。假设电机转速变化非常缓慢，式(5)可简化为

1.2 车窗机械传动

本文研究对象为绳轮式电动玻璃升降器[5]。直流电机输出轴，通过涡轮蜗杆机构将转矩传递到卷线轮。电机输出轴和蜗杆同轴，卷线轮和涡轮同轴[6]。卷线轮通过钢丝绳带动车窗玻璃升降。

传动系统力的平衡方程[7]为

式中：mg为车窗玻璃质量；g为重力加速度；Ff为车窗玻璃受到的摩擦力；Fc为障碍物夹持力；KN为障碍物刚度；Δx为障碍物形变；D为卷线轮直径；K为涡轮蜗杆传动比。电机角速度[8]为

式中：P为电机旋转一圈产生的霍尔信号个数；wd为霍尔信号脉冲宽度。

1.3 利用脉宽积分判断防夹

用脉宽曲线的积分面积作为防夹判断的标准，主要的错误信号来源于车身振动造成的脉宽信号噪声。首先假设车身没有振动的理想情况下，车窗上升过程中遇到障碍物。根据该情况下脉宽积分的面积值，作为积分面积阈值Sth。综合式(4)、式(6)、式(7)、式(8)，化简可得

根据式(9)，求出信号脉宽和障碍物形变之间的关系为

根据欧洲法规，防夹力最大阈值为F≤100N。积分面积的阈值Sth为

Sth随着工况的不同而发生改变，具体数值参见表1。

车身振动会产生脉宽信号的噪声。在实际情况下，积分面积s为

式中：x0为积分开始的位置；x1为积分结束的位置；x为当前积分位置。

表1 积分面积阈值选取

2 脉宽测量噪声的统计特性

图1 霍尔信号波形

图2 霍尔信号脉宽波形

汽车以一定速度行驶时，路面不平度会产生激励，导致车身及其车窗玻璃振动。同时，发动机振动也会传递到车窗玻璃。由于车窗受到的上升阻力是通过霍尔信号脉宽得到的，故有必要使用滤波算法。

某款汽车以60km/h速度行驶在沥青路面上，车窗整个上升行程中测得的脉宽曲线如图2所示。从图中可知，车窗启动阶段，霍尔信号脉宽波动较大，因为此时车窗玻璃在车门内饰板内部，摩擦力逐渐减小。车窗启动阶段不是防夹区域，这一段的霍尔信号不进行处理。车窗上升阶段，摩擦力逐渐稳定，霍尔信号脉宽波动较小。霍尔信号脉宽噪声的功率谱密度如图3所示。分析霍尔信号脉宽噪声的统计特性可知，噪声的频率主要集中在15～35Hz频段，而在0～15Hz步骤的噪声较小。如果采用卡尔曼滤波算法，就无法分辨高频和低频噪声。而高斯滤波具有较好的低通特性，可在尽量保留原波形的基础上，滤除一部分高频噪声。因此，防夹算法采用高斯滤波更为合适。

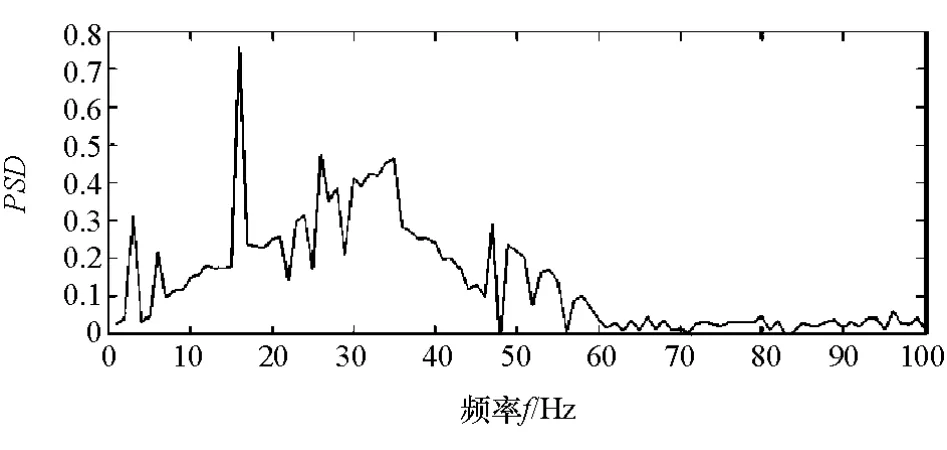
图3 噪声的功率谱密度

3 防夹力实时估计

3.1 高斯滤波

3.1.1 一维线性高斯滤波

均值为0，方差为σ的一维高斯滤波器[9]为

其中σ取值越大时，滤波平滑程度和波形失真越大；σ取值越小时，滤波平滑程度和波形失真越小。σ具体取值须综合考虑滤波效果和运算量[10]。

式中s(x)为f(x)经过高斯滤波后的值。

3.1.2 高斯滤波离散化

还记得去年采访时Sarah说过她“逃学”到意大利学习厨艺的事情，这次出任VIA的新任教员应该可以说是Sarah找回了自己的“初恋”：意大利葡萄酒。从和她的讨论中看得出她对意大利葡萄酒的热爱。而且早在2015年她就成为VIA认证“意大利葡萄酒大使（IWA）”，离她考取WSET Diploma才不过两年时间。

霍尔信号的脉冲值是离散型随机变量，因此须将一维高斯滤波器离散化[11]。

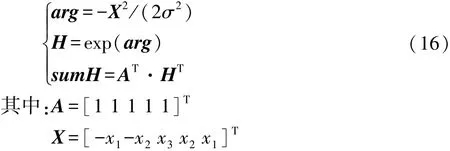
式中：arg，H，sumH 为中间变量；x1，x2，x3为高斯分布中可信度为95%的置信区间中的3个概率。

式中G(x)为高斯卷积核的元素。

利用该离散化的一维高斯滤波器对霍尔信号脉宽进行滤波：

式中：F(x)为霍尔信号的脉宽；x为霍尔信号的脉冲个数；h(x)为滤波后的结果。

3.2 近似积分

车窗玻璃在上升过程中，接触到障碍物之后，转速下降，霍尔信号脉冲宽度增加，在脉冲宽度曲线上表现为一个上升沿。由于障碍物刚度一般在10N/mm左右，脉冲宽度会以一定的斜率上升一段时间。在脉冲宽度上升的过程中，进行积分运算。可进行积分的条件为

式中g1(x)为霍尔信号脉冲宽度实际测量值。

在脉冲宽度开始上升时，求取积分区域的下限：

参照式(12)，进行防夹的判断。积分面积阈值的选取参见表1。

根据MVSS18法规要求，当电压超出9～16V范围时，防夹车窗系统进入降级模式，即仅保留车窗手动上升、手动下降的功能，自动上升功能取消，同时不要求具备防夹功能。当汽车行驶在颠簸路面时，增加积分阈值，防夹力会增大，防夹力阈值F依然小于100N，这样可确保车窗能够正常关闭。

4 dSPACE快速控制原型试验分析

在MATLAB/Simulink环境下建立电动车窗仿真模型，然后下载到dSPACE的ControlDesk中，利用RTI接口将电动车窗玻璃升降器、功率放大板与ControlDesk连接起来，进而测试本文中提出的防夹算法。仿真模型包含控制算法、RTI接口，实物包括电动车窗玻璃升降器、车窗按键开关和功率放大板(用来放大RTI输出的控制信号从而控制直流电机)。车窗电机输出两路具有相位差的霍尔信号，控制算法部分检测霍尔信号的相位差和脉冲宽度，进而做出是否防夹的判断。dSPACE中ControlDesk模型如图4所示。

图4 ControlDesk模型

通过改变直流电源的输出电压、改变安装玻璃升降器的台架振动情况和施加障碍物，可分别模拟车载蓄电池电压波动、路面颠簸和障碍物夹持等多种情况。

测试工况中，障碍物按照欧洲防夹标准设计，刚度为10N/mm，采用橡胶棒作为障碍物。ControlDesk中的disPlay工具能够采集霍尔信号脉宽的信息，并将数据存储为.csv格式。为便于观察试验结果，须将存储霍尔信号的脉冲宽度的.csv文件转换成excel文件，然后输入MATLAB中绘制结果曲线。在本文算法中，脉冲宽度曲线经过滤波和积分后，须转换成积分面积。脉冲宽度与阻力值相关，积分面积和夹持力做功相关。表2列出了两种滤波器的调整参数。表2中qV为过程噪声协方差，qT为测量噪声协方差。

4.1 普通工况

普通工况即电源电压为12V、汽车以一定速度行驶在沥青路面或水泥路面，此时车身振动较小。车窗玻璃在自动上升过程中遇到障碍物时，霍尔信号脉宽会增大。分别统计基于卡尔曼滤波的防夹算法和本文防夹算法的运算次数，本文中需要统计的公式为式(10)～式(22)，其余公式为化简所需要的，不计入最终运算次数。表3列出两种算法的运算量对比。由表3可知，与基于卡尔曼滤波的防夹算法相比，本文防夹算法运算次数虽然处于同一数量级，但运算量略有减小。

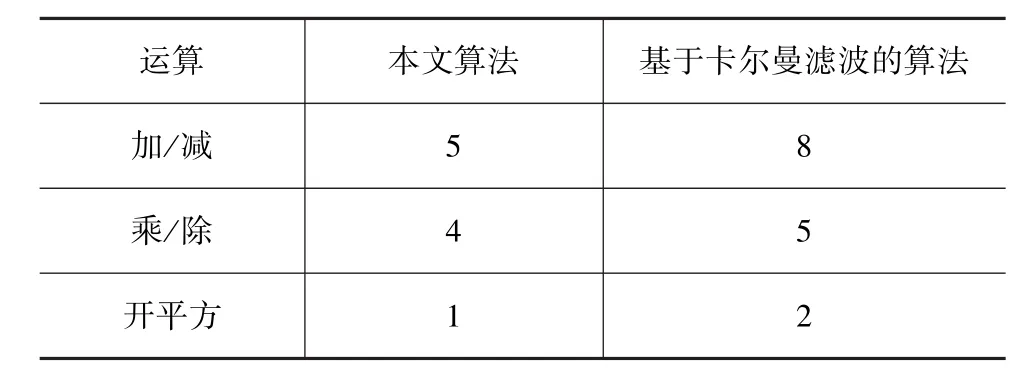
表3 两种算法的运算量对比

图5示出两种防夹算法仿真结果。图5(c)中，积分面积达到阈值时，就满足了防夹的判断条件。图5(d)中，利用霍尔信号脉宽换算得到的夹持力达到阈值时，同样满足防夹的判断条件。仿真结果表明，两种防夹算法都可以准确地做出防夹判断。

4.2 电压波动

正常情况下，车窗电机的驱动电压为12V。但是蓄电池的电压会随着车内电器负载功率和蓄电池电量等因素发生变化。车窗电机正常工作的电压范围为9～16V。

改变直流电源的输出电压，模拟车载蓄电池电压分别为10和14V两种工况。两种工况下本文防夹算法的结果如图6和图7所示。从图中可以看出，在不同的电压下，本文中提出的防夹算法均能根据积分面积做出准确的防夹判断。

4.3 颠簸路面

颠簸路面包括比利时路面和砂石路面等。在这种路面上，车身振动较大，霍尔信号脉宽的噪声幅值也较大。霍尔信号脉宽曲线的特征之一就是上升沿，上升沿的判断方式见式(19)。汽车以一定速度行驶时，车窗自动上升过程中，上升沿个数与路况的相关性最强。因此可用上升沿个数作为路面分类属性值。通过对安装玻璃升降器的台架施加一定的振动，可模拟汽车行驶在颠簸路面时电动车窗玻璃受到干扰的情况。

图5 防夹算法仿真结果

通过某款轿车在沥青路面和颠簸路面上行驶时采集到的脉宽信号曲线，作为训练样本。根据样本值得出的分类器如表4所示。表中C＝1为真，C＝0为假。电动车窗自动上升过程中，如果上升沿的统计次数超过一定值，就判断当前路况为颠簸路面，需要增大积分面积阈值。图8为颠簸路面工况两种防夹算法仿真结果。由图8(e)可知，当前工况下有22次上升沿，所以C＝1，根据路面分类器，当前路面属于颠簸路面，且当前工况下积分阈值Sth＝220。

在这种工况下本文中提出的防夹算法和基于卡尔曼滤波的防夹算法，有一定的区别。由图8(c)可见，由于采用了积分法，可有效地滤除由瞬时抖震造成的防夹力突变。试验结果表明，汽车行驶在颠簸路面时，该算法可准确做出防夹判断，具有较好的鲁棒性。由图8(d)可见，基于卡尔曼滤波的防夹算法产生了两次误防夹。由此可知，在颠簸工况下，本文的防夹算法的鲁棒性较高。

4.4 深坑路面

汽车行驶在深坑路面或通过减速带时，车身会发生振幅较大的瞬时振动，霍尔信号脉宽曲线表现为尖峰脉冲。通过对安装玻璃升降器的台架施加瞬时振动，可模拟汽车行驶在深坑路面的工况。

在这种工况下，本文中提出的防夹算法和基于卡尔曼滤波的防夹算法会有较为明显的区别。图9为深坑路面工况下两种防夹算法仿真结果。由图9(c)可见，即使车身发生振幅较大的瞬时振动，本文的防夹算法依然可做出准确的防夹判断。由图9(d)可见，基于卡尔曼滤波的防夹算法，由于无法对尖峰脉冲进行识别，故出现了误防夹。由此可知，在深坑路面工况下，本文的防夹算法鲁棒性较好。

图6 U＝10V防夹算法仿真结果

表4 分类器

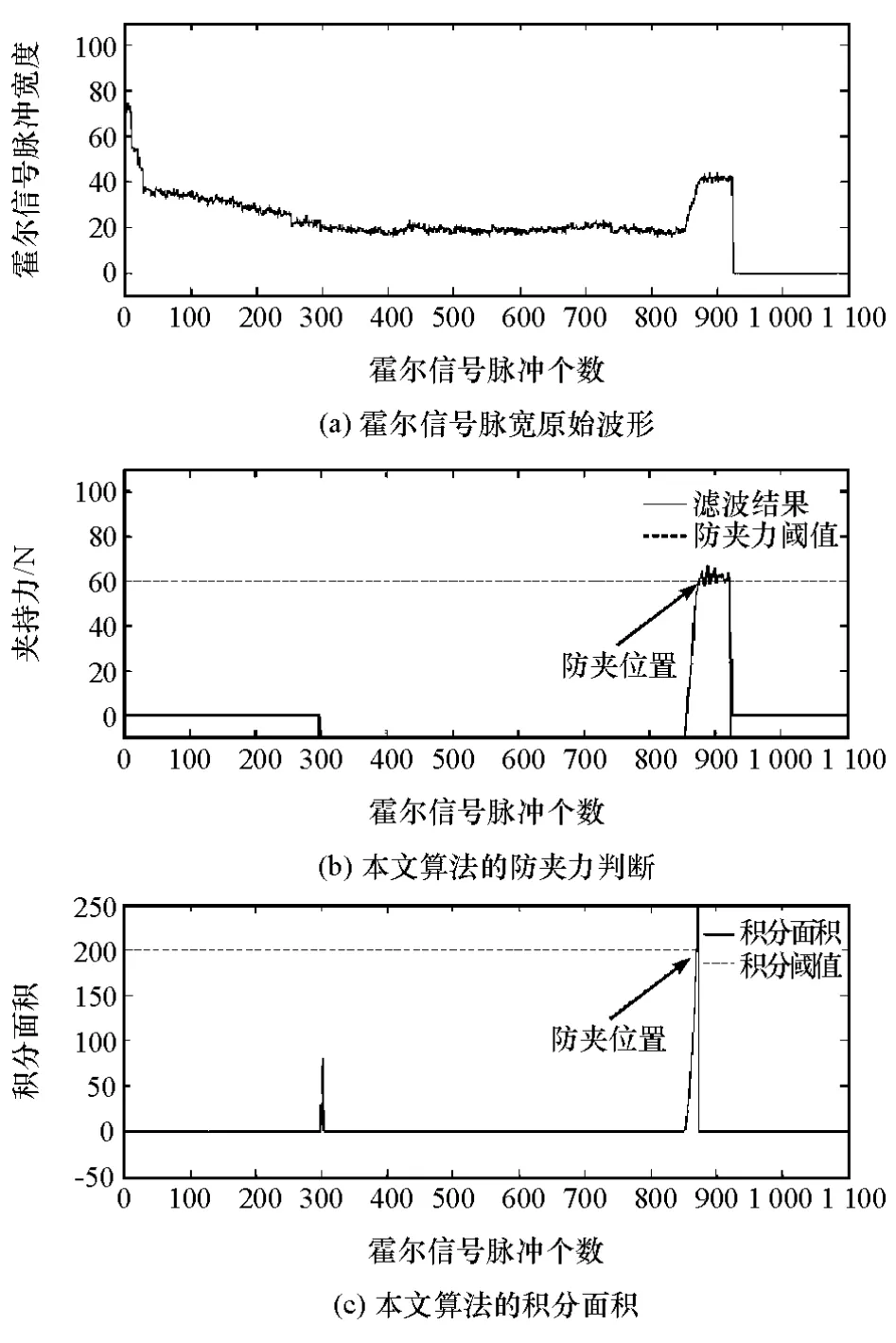
图7 U＝14V防夹算法仿真结果

4.5 鲁棒性数学分析

图10示出了卡尔曼滤波算法和积分算法对尖峰脉冲的处理结果。卡尔曼滤波算法的核心是通过测量值和上一次的估计值的协方差，做出下一状态的最优估计值，协方差不断进行迭代更新。这种算法对尖峰噪声的滤除效果不明显。由图10可知，卡尔曼滤波算法仅使峰值稍有下降，而积分法则对尖峰脉冲具有很好的滤除效果。但积分法的弊端是对缓慢增长的阻力滤除效果不明显，且有一定的累积误差。

图8 颠簸路面工况防夹算法仿真结果

图9 深坑路面工况防夹算法仿真结果

图10 尖峰噪声滤波分析

5 结论

提出一种基于高斯滤波和近似积分的防夹算法。高斯滤波可有效滤除脉宽信号尖峰噪声，减少其幅值，但滤波后尖峰噪声依旧存在。车窗自动上升过程中遇到障碍物时，霍尔信号脉宽曲线会立即上升。通过检测上升沿，判断积分开始的位置，利用积分面积是否达到阈值作为防夹判断的标准。与基于卡尔曼滤波的防夹算法相比，本文的防夹算法运算量略有减少。仿真结果证明，汽车行驶在颠簸路面和深坑路面的工况下时，与基于卡尔曼滤波的防夹算法相比，本文的防夹算法运算量更小、鲁棒性更好。

本文的防夹算法没考虑空气阻力和悬架刚度等因素对电动车窗直流电机输出的霍尔信号的影响。下一步研究要综合考虑电压、路面、空气阻力和悬架等多种因素，提高防夹算法的鲁棒性。

[1] EU Council Directive.7460EEC：On the approximation of the laws of themember states relating to the interior fittings ofmotor vehicles[S].1973.

[2] RAW S，LEE H J，PARK JB，etal.Practical pinch detection algorithm for smart automotive power window control systems[J].IEEE Trans.Industrial Electronics，2008，55(3)：1376-1384.

[3] SOLLMANN M，SCHURR G，DUFFY-BAUMGAERTNER D，et al.Anti pinch protection for power operated features[C].SAE Paper 2004-01-1108.

[4] GUI Zhonghua，HAN Fengqin.Wavelet packet-maximum entropy spectrum estimation and its application in turbineps fault diagnosis[J].Automation of Electric Power Systems，2004，28(2)：62-66.

[5] 封贵阳.汽车车窗控制系统及其防夹算法的研究[D].哈尔滨：哈尔滨工业大学，2014.

[6] 马伟泽，张申科，汪宏杰.采用霍尔传感器的汽车电动车窗防夹设计[J].汽车工程，2008，30(12)：1122-1124.

[7] 戴国骏，张翔，张怀相，等.电动车窗防夹系统的建模与实现[J].汽车工程，2008，30(6)：539-542.

[8] 傅侃，刘博，李二涛.基于LIN总线防夹电动车窗的研究与设计[J].杭州电子科技大学学报，2008，28(3)：39-42.

[9] 王振华，窦丽华，陈杰，等.一种尺度自适应调整的高斯滤波器设计方法[J].光学技术，2007，32(3)：395-397.

[10] 许景波.高斯滤波器逼近理论与应用研究[D].哈尔滨：哈尔滨工业大学，2007.

[11] Christof Chlebek， Jannik Steinbring， Uwe D Hanebeck.Progressive Gaussian filter using importance sampling and particle flow[J].IEEE International Conference on Information Fusion，2016，42：2043-2049.