板簧Bouc-Wen迟滞模型的仿真与试验研究∗

章 杰，吴 茵，张邦基，张 农，刘献忠

(1.湖南大学，汽车车身先进设计制造国家重点实验室，长沙 410082； 2.合肥工业大学汽车与交通工程学院，合肥 230009)

前言

板簧是矿用车等特种车辆非独立悬架系统的弹性元件。车辆在不平路面行驶时，板簧承受动载荷产生变形并表现出迟滞特性；板簧受到垂直载荷冲击时，簧片间产生干摩擦力，加剧其迟滞特性。迟滞特性使板簧呈现刚度和阻尼的非线性，对车辆平顺性和行驶安全性产生重要影响，因此有必要建立合理的板簧动态力模型并进行迟滞响应分析[1-4]。

多年来国内外学者对板簧动力学特性进行了广泛研究。文献[5]中考虑片间接触影响，用ANSYS有限元软件建立板簧动力学模型，分析不同摩擦因数下的板簧迟滞特性；文献[6]中用ANSYS建立板簧有限元模型，并结合ADMAS整车多体动力学模型分析迟滞特性对车辆平顺性的影响；文献[7]中采用扩展三连杆方法，用ADMAS软件对板簧刚度特性和整车性能的影响进行分析；文献[8]中用ANSYS有限元软件分析不同摩擦因数对板簧刚度特性的影响，并根据仿真结果研究板簧非线性回复力对车辆振动的影响；文献[9]中用ADMAS软件建立钢板弹簧动力学模型，基于遗传算法反求出影响板簧刚度特性的关键参数，提高了仿真模型的准确性。文献[10]中运用有限元方法建立渐变板簧的多柔体动力学模型，分析板簧的迟滞特性和动态力；文献[11]中采用欧拉梁理论分析板簧刚度特性，并与有限元模型对比分析验证结果的正确性；文献[12]中采用有限单元法建立板簧非线性模型，并进行车辆多体动力学仿真分析；文献[13]中采用ANSYS软件建立具有锥形截面的板簧有限元模型，分析了少片簧的迟滞特性。由上述研究看出，目前主要采用有限元和多体动力学方法研究板簧的非线性刚度和阻尼特性，但这些建模方法需建立庞大节点数目的有限元模型，导致计算效率低，不适合应用于整车模型进行动力学仿真分析。

采用Bouc-Wen模型分析力学迟滞现象，主要应用于建筑结构、复合材料和土体动力学等领域[14]，在机械领域主要研究磁流变阻尼器的力学特性，在车辆悬架系统上的研究则较少[15]。本文中提出一种基于Bouc-Wen迟滞模型的钢板弹簧动力学建模方法，建模简便，计算效率高，能真实地反映板簧刚度和迟滞特性，适用于车辆动力学仿真分析。

1 板簧迟滞Bouc-Wen模型

1.1 Bouc-W en模型

Bouc-Wen迟滞模型[16]是1阶非线性微分方程，其表达式为

式中：R为系统迟滞回复力；x为系统响应位移；z为系统迟滞位移。模型中有6个关键参数(α，k，A，β，γ和n)：α为板簧屈服后与屈服前的刚度比值(0＜α＜1)，主要影响滞回圈面积，αk为板簧的线性刚度(k为初始刚度)；A，β，γ和n为模型形状参数，其中n为滞回曲线光滑程度系数，由文献[17]可知参数n的灵敏度最低，因此在进行模型参数辨识时可先固定n值。

1.2 模型参数辨识

采用最小二乘法进行板簧模型关键参数辨识，首先确定n值，通常取n＝1[17]；然后，由板簧静态加载试验获取板簧线性刚度kl；再由kl＝αk，根据参数范围初选α，得到k。

由式(1)可变形得到板簧迟滞位移：

式中：t0为试验数据初始点时刻；ti为终止点时刻。对式(4)进行简化处理可以得到：

其中：

通过试验数据xi和式(3)得到zi，用数值求解方法可求得 b1i，b2i和 b3i，式(5)即为关于 A，β 和 γ 的线性方程。根据处理的数据选定积分初始点t0和终止点ti，得到N个关于A，β和γ的线性方程组，此时参数A，β和γ可表示为最小二乘问题求解最优值：

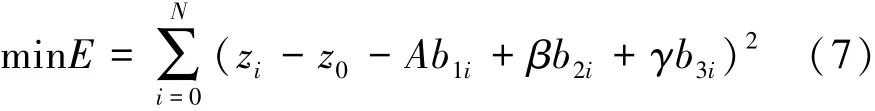
式中N为试验采集的数据长度。

对式(7)分别对A，β和γ求偏导，令所得3个方程等于零，得式(8)，求解该方程即可得A，β和γ。

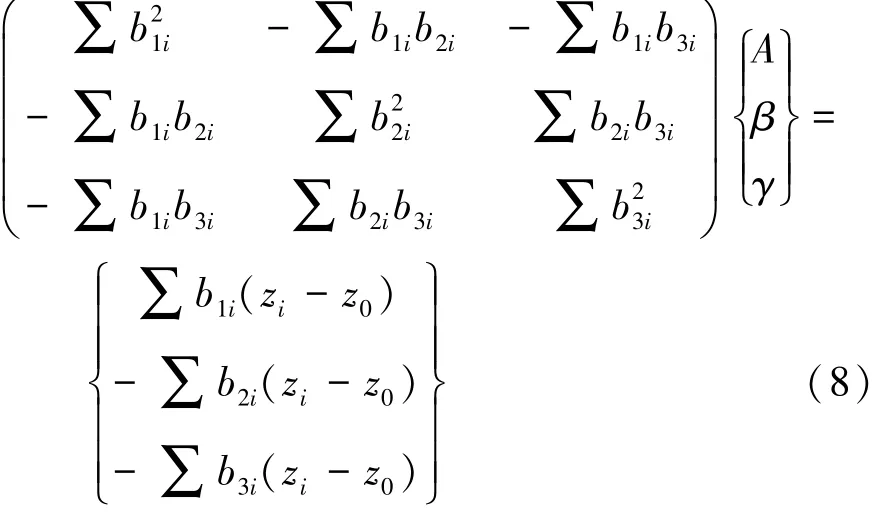
为进一步确定参数α和k，可改变不同的数值。当均方根值误差为最小时，此时参数α，k，A，β和γ为最终辨识结果。图1为板簧参数辨识流程。

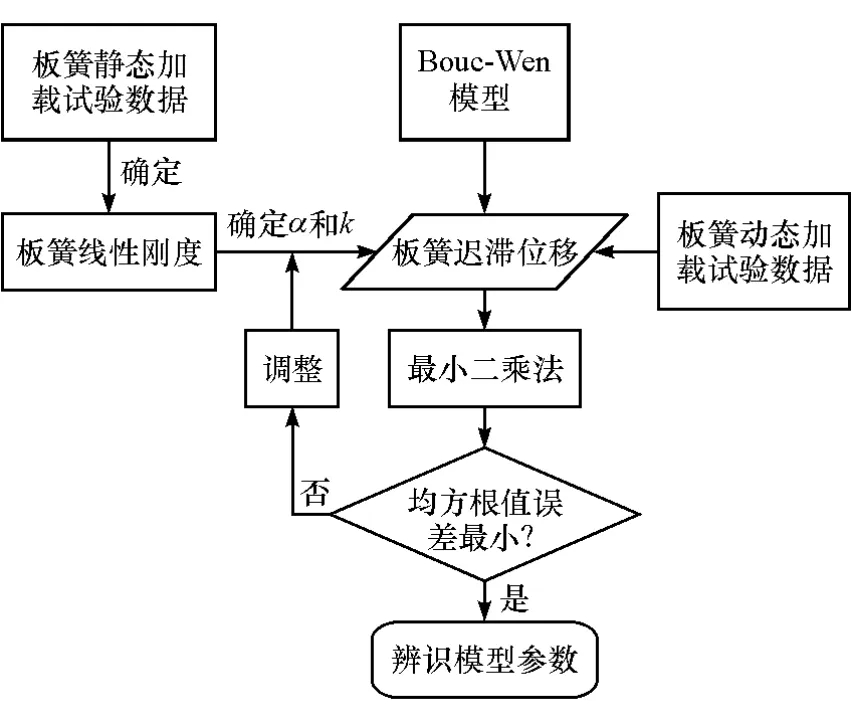
图1 板簧参数辨识流程

2 静/动态加载试验与模型验证

2.1 静/动态加载试验及迟滞特性分析

对某矿山车辆前/后悬架系统的板簧进行静/动态加载试验，图2为试验系统。静态加载试验中载荷由零逐渐增大到某个值，再逐渐卸载，得到的力位移曲线如图3所示。分析可知：曲线的变形初始值由加载装置的质量产生，可在后续数据处理中消除；前后板簧均表现出明显的迟滞现象；曲线的斜率为板簧的线性刚度，后板簧线刚度大于前板簧线刚度；运用四点法[18]计算出前后板簧线性刚度分别为129.2和172.4N/mm。

图2 板簧试验系统

为分析板簧迟滞特性，进行动态加载试验，按照等幅 变频和等频 变幅两种方式加载正弦信号。

加载幅值恒定为4mm，加载频率分别为0.5，1，2，4 和 6Hz，得到等幅 变频试验结果，如图4所示(限于篇幅，仅附前板簧试验结果)。当加载频率处于低频范围时，板簧动态力滞回曲线仅有微小差异，符合文献[19]中得出的在15Hz以下的加载频率对板簧力 变形迟滞曲线影响不大的结论。

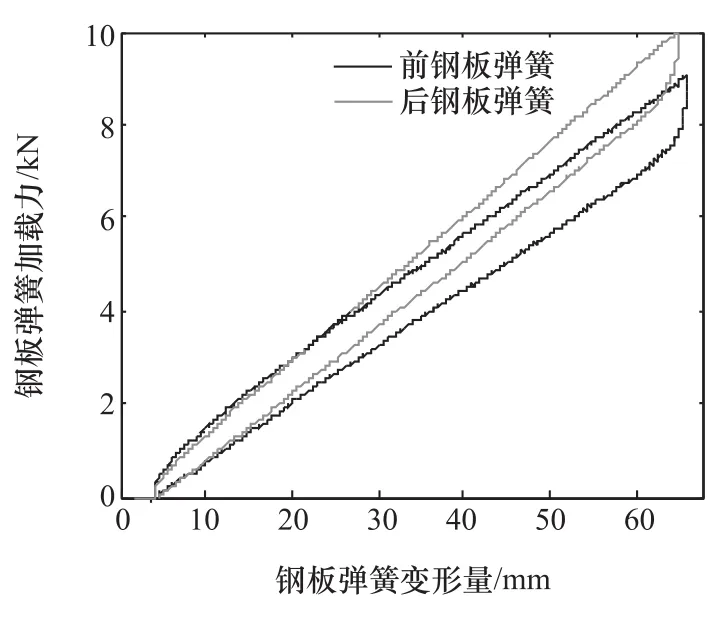
图3 前/后板簧静态加载试验结果

图4 前板簧等幅 变频加载试验结果

按照上述结论，加载频率恒定为1Hz，幅值分别定为 1，2，4，8 和 16mm，得到前后板簧等频 变幅试验结果，如图5和图6所示。加载幅值越小，滞回曲线斜率越大，表明板簧在小幅振动时动态刚度较大；加载幅值越大，滞回曲线斜率越小，越接近钢板弹簧静态试验的加载和卸载边界线，表明钢板弹簧在大幅振动时动态刚度较小。当振幅达到一定值时，板簧动态刚度会接近静态线性刚度。

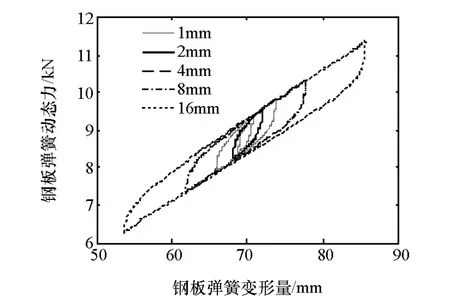
图5 前板簧等频 变幅加载试验结果

2.2 Bouc-W en迟滞模型验证

运用上述辨识方法和试验数据进行模型关键参数辨识，结果如表1所示。前、后钢板弹簧线性刚度辨识结果为132.6和167.4N/mm，与2.1小节通过试验数据获取的结果129.2和172.4N/mm比较接近，误差＜3%，表明了辨识结果的准确性。为进一步验证Bouc-Wen模型的正确性，对板簧等频 变幅动态加载试验进行仿真，图7和图8为前后板簧的仿真与试验结果对比，可以看出，仿真和试验结果吻合较好，能够真实地反映钢板弹簧的迟滞特性，从而验证了模型的正确性。

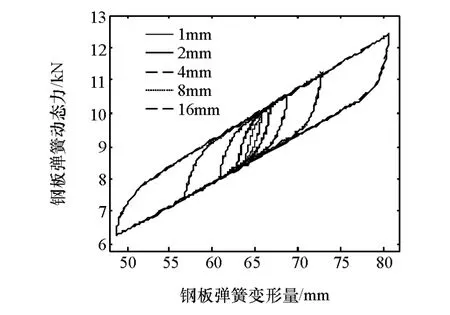
图6 后板簧等频 变幅加载试验结果

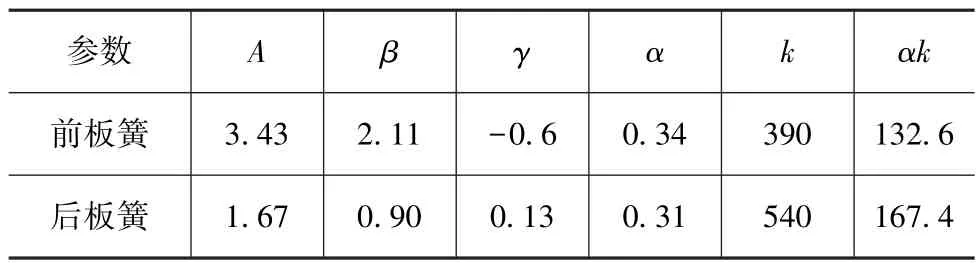
表1 前后板簧参数辨识结果

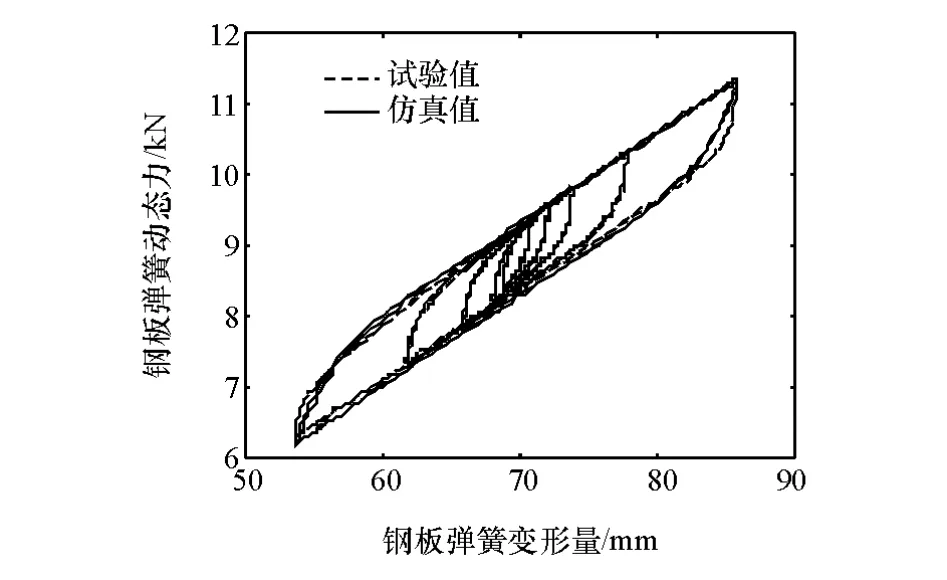
图7 前板簧等频 变幅加载的仿真与试验结果

3 包含板簧Bouc-Wen模型的整车动力学建模与验证

3.1 整车动力学建模

为研究板簧的迟滞特性对车辆性能的影响，建立包含板簧Bouc-Wen模型的整车模型，如图9所示。7个自由度分别为簧上质量的垂向位移xs、俯仰角θ、侧倾角φ和4个车轮的垂向位移xui(i＝A，B，C和D)。根据牛顿第二定律，建立包含板簧迟滞特性的整车系统动力学方程：

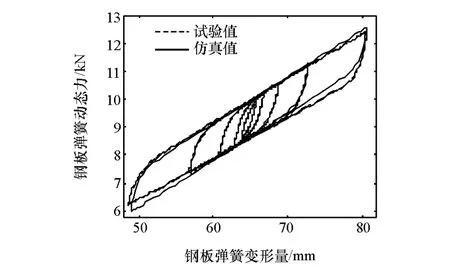
图8 后板簧等频 变幅加载的仿真与试验结果

式中：X＝[xsθφxuAxuBxuCxuD]T为位移向量；M为质量矩阵；C为阻尼矩阵；K为线性刚度矩阵；F为具有迟滞位移和路面激励的外力矩阵。F的状态空间方程可表述为

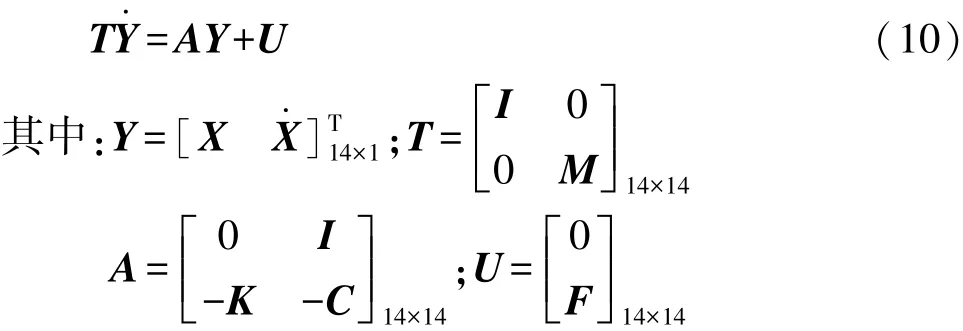
以某矿山车辆参数作为仿真用参数，见表2。

3.2 整车模型试验验证

为验证该整车模型的正确性，对样车进行60，120和160mm 3种高度的前轮跌落试验(见图10)，采集车辆自由振动时质心的加速度响应信号，如图11～图13所示。

由试验结果可以看出，随着跌落高度增加，车辆质心加速度明显增大，板簧受到的垂直冲击载荷越大，自由振动响应越大；同时，在3种不同工况下，仿真和试验结果趋势均一致，吻合良好，验证了整车模型的正确性。

图10 整车跌落试验

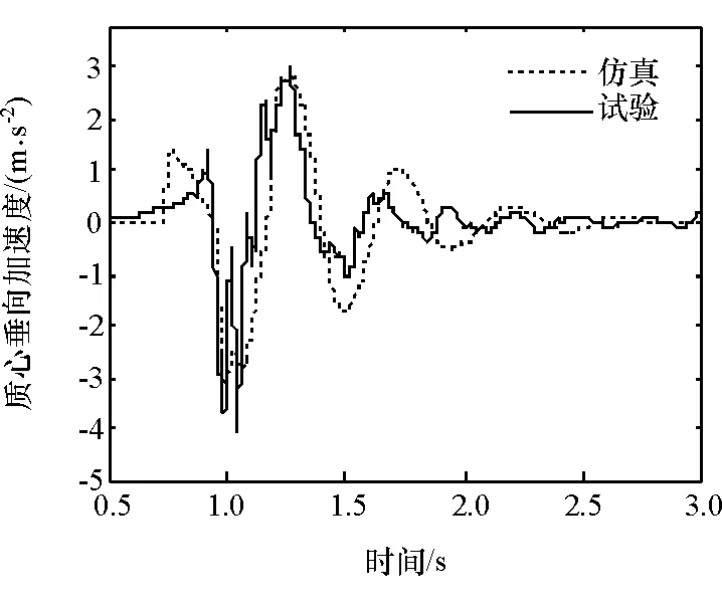
图11 60mm跌落试验质心加速度

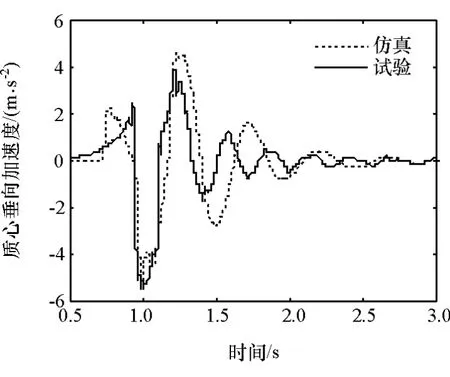
图12 120mm跌落试验质心加速度

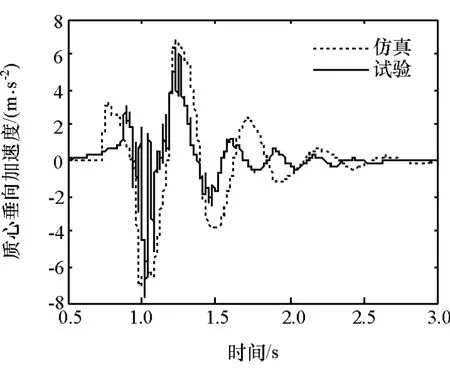
图13 160mm跌落试验质心加速度

4 迟滞特性对整车性能影响分析

研究板簧迟滞特性对整车性能的影响，以质心加速度均方根值作为整车平顺性评价指标，以悬架动行程和轮胎动载荷作为安全性评价指标并与不考虑迟滞的线性模型对比。仿真中采用四轮相关的路面谱激励[20-21]，分别进行A和E级路谱仿真。由于A级路况较好，车速分别为40，50和60km/h；E级路况较差，车速分别为10，20和30km/h。限于篇幅，只给出A级路面60km/h和E级路面30km/h的质心加速度、悬架动行程和轮胎动载荷时域图(见图14～图19)，其中 HM(hysteresismodel)和 LM(linear model)分别为迟滞模型和线性模型。不同速度下对比结果见表3。

由图14～图16可见，A级路面激励下迟滞车辆模型的质心加速度比线性车辆模型大，悬架动行程和轮胎动载荷比线性车辆模型小。因为A级路面高频小幅值成分占比大，板簧动刚度在小幅值激励时具有较强的动刚度，具体表现为悬架偏硬，可以看出板簧在高速公路等较好路面上对车辆的平顺性有一定不利影响，但对车辆的行驶安全性有利。

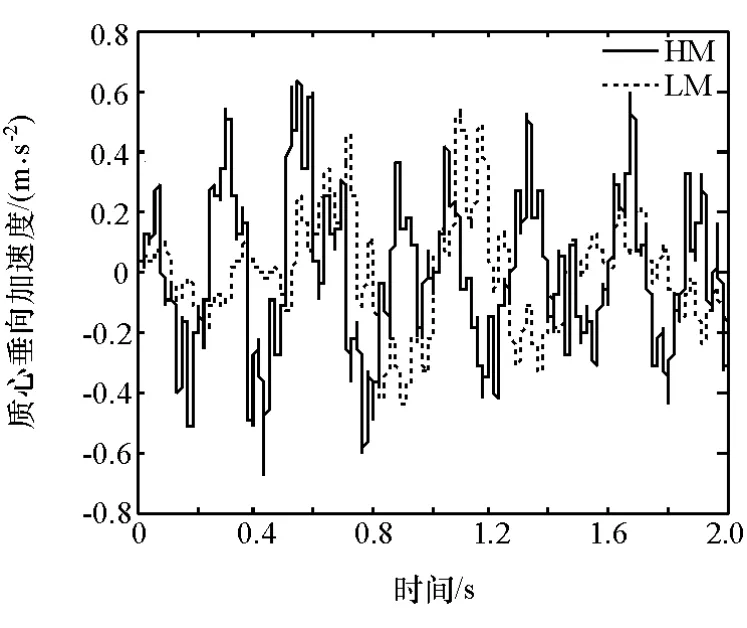
图14 60km/h A级路面质心加速度

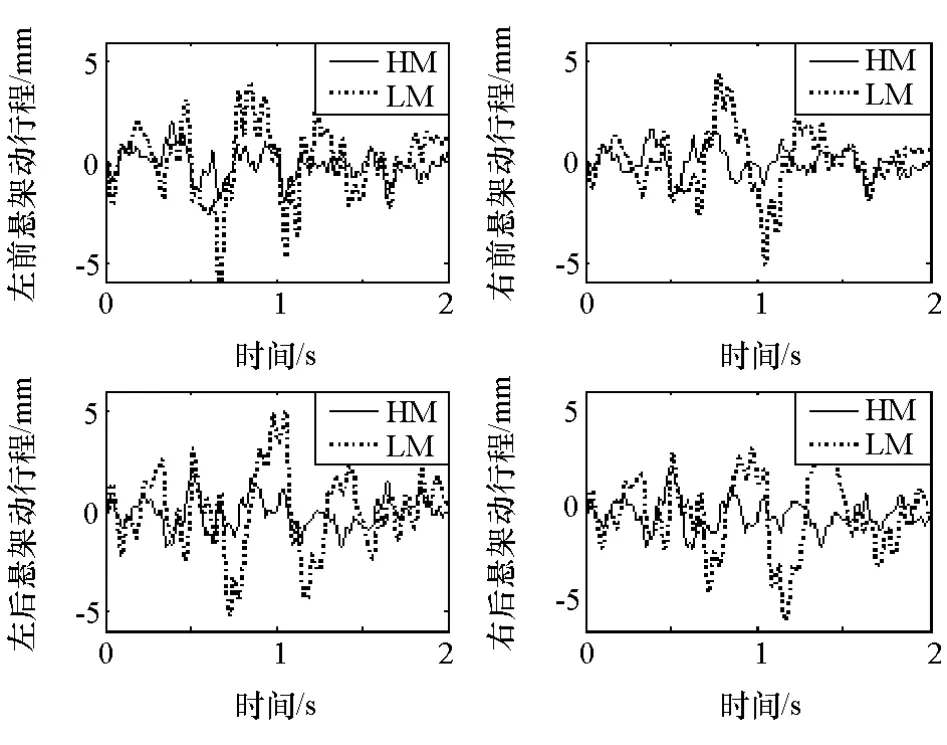
图15 60km/h A级路面悬架动行程

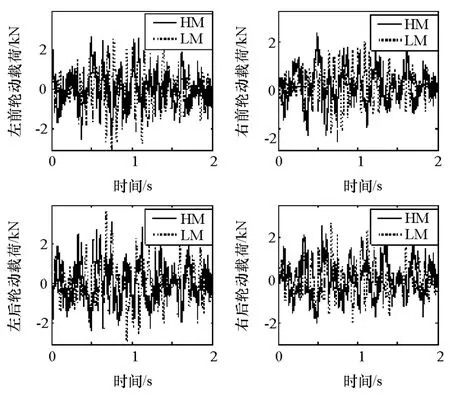
图16 60km/h A级路面轮胎动载荷

图17 30km/h E级路面质心加速度

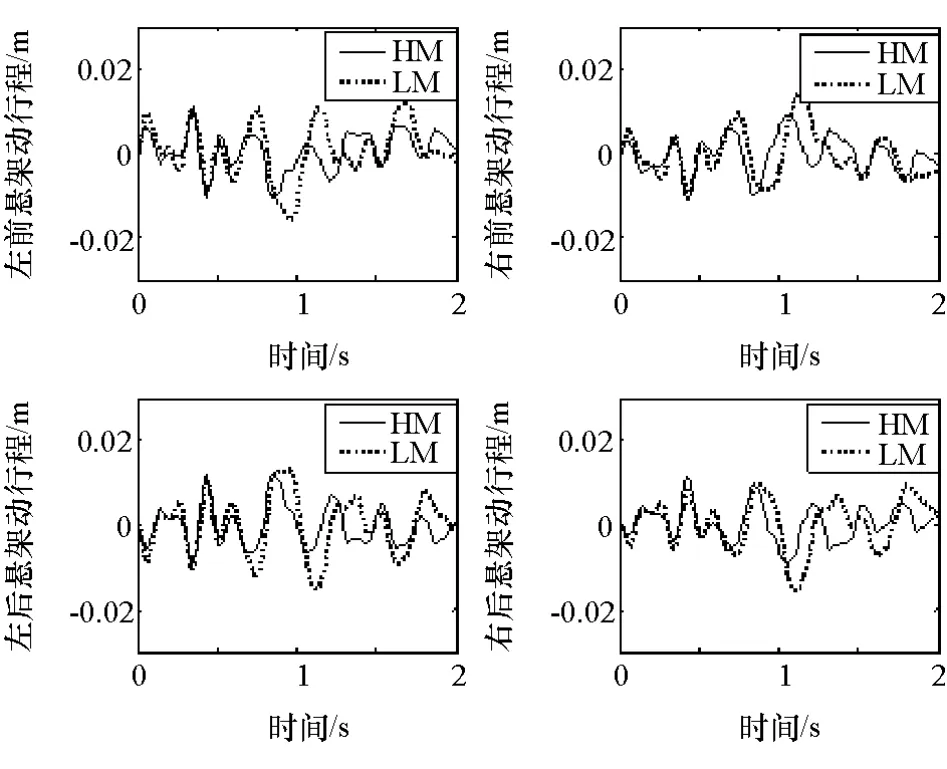
图18 30km/h E级路面悬架动行程

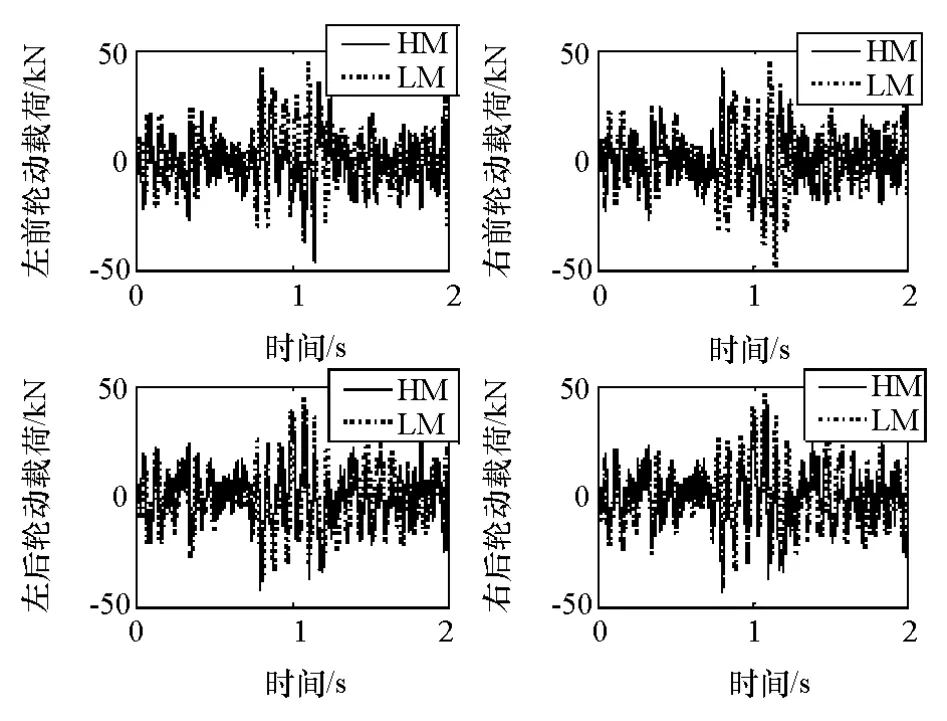
图19 30km/h E级路面轮胎动载荷

由图17～图19可见，E级路面激励下迟滞车辆模型的质心加速度、悬架动行程和轮胎动载荷均要小于线性车辆模型。因为E级路面低频大幅值成分占比大，在大幅值激励时板簧的动刚度会减小，趋近但大于其静态刚度，所以悬架动行程和轮胎动载荷比线性模型结果要小。由于钢板弹簧片之间的干摩擦形成的阻尼力(滞回曲线面积)较大，耗散的能量较多，导致质心处加速度比线性模型结果要小，可以看出在较差的路面上钢板弹簧对车辆的平顺性和行驶安全性均有利。

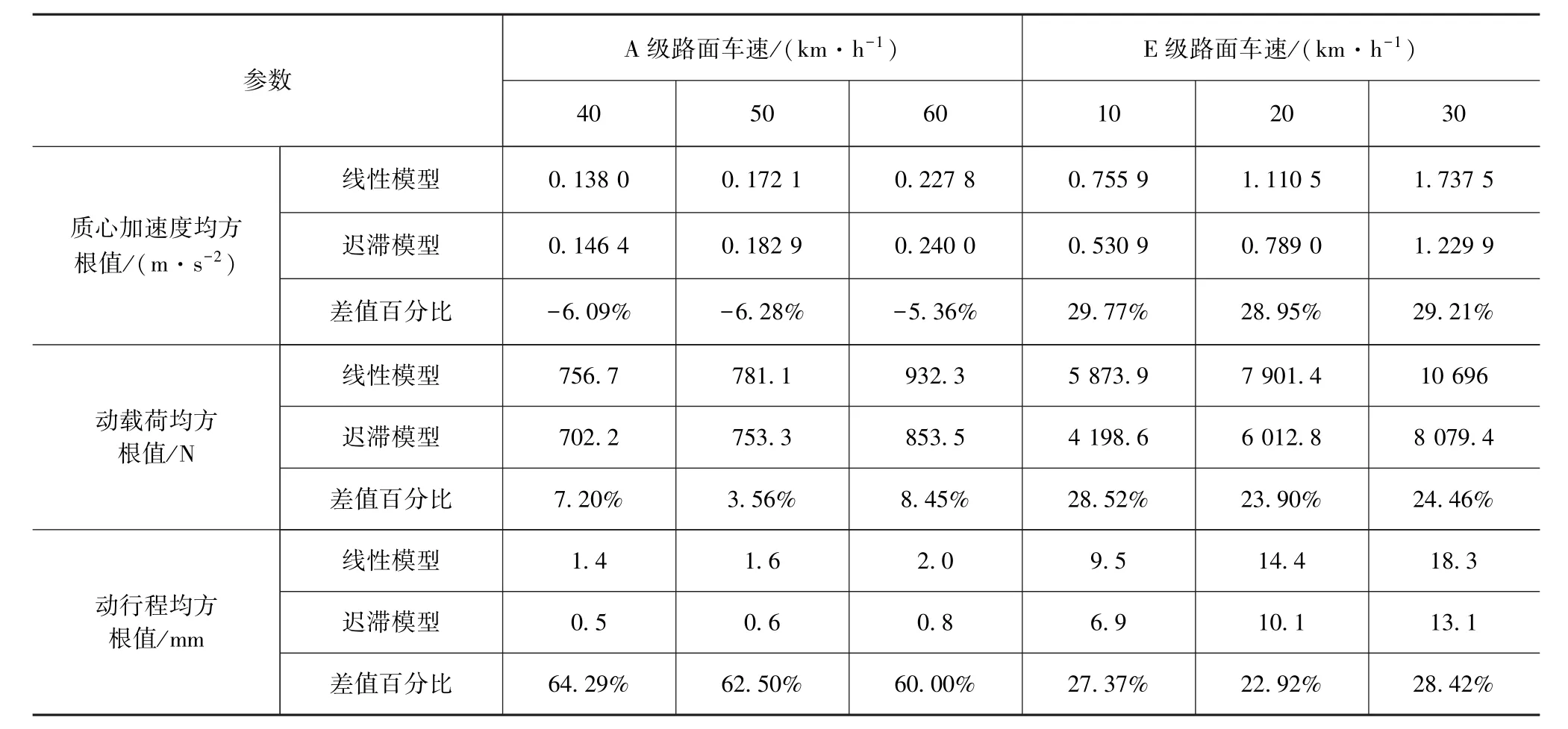
表3 路谱仿真结果

5 结论

本文中建立了板簧Bouc-Wen迟滞模型，运用最小二乘法进行模型关键参数辨识，辨识结果与试验结果比较接近，验证了迟滞模型的正确性。建立考虑迟滞特性的整车模型并试验验证其正确性，对比分析了板簧迟滞特性对整车性能影响。仿真和试验结果表明：(1)在低频范围内，加载频率对钢板弹簧迟滞特性有微弱影响；(2)在小幅值时板簧具有较大动态刚度；(3)在良好路面上，板簧迟滞特性对车辆平顺性有一定不利影响；在较差路面上，板簧迟滞特性能提高车辆平顺性；(4)板簧迟滞特性能够提高车辆行驶安全性。因此，行驶工况较差的大、中型货车应多采用板簧悬架，其迟滞特性能使车辆兼顾一定的舒适性和行驶安全性。

[1] KONG K S，OMAR M Z，CHUA L B.Stress behaviour of a novel parabolic spring for light duty vehicle[J].International Review of Mechanical Engineering，2012，6(3)：617-620.

[2] TAJIMA J， MOMIYAMA F， YUHARA N.A new solution for twobag air suspension system with leaf spring for heavy-duty vehicle[J].Vehicle System Dynamics，2006，44(2)：107-138.

[3] SHEPELYAKOVSKIIK Z，ISMAILOV R R，LITVIN A N，et al.New technology for heat treating leaf-spring sheets for trucks[J].Metal Science and Heat Treatment，1992，34(2)：97-101.

[4] 凌荣江.汽车板簧的建模及非线性分析[D].南京：南京航空航天大学，2008.

[5] 丁能根，马建军.钢板弹簧迟滞特性的有限元分析[J].汽车工程，2003，25(1)：13-14.

[6] 席敏，刘桂萍，雷飞，等.考虑片间接触的汽车钢板弹簧动力学建模[J].汽车工程，2012，34(8)：751-755.

[7] 李凌阳，张云清，覃刚，等.钢板弹簧建模方法研究[J].汽车工程，2013，35(7)：660-666.

[8] 张智，卢剑伟，陈渊锋，等.不同摩擦系数的钢板弹簧动态特性分析[J].汽车工程学报，2013，3(2)：94-99.

[9] 鞠成超，韩旭，刘桂萍.钢板弹簧离散梁动力学参数反求[J].汽车工程，2009，31(9)：860-863.

[10] MOON ID，YOON H S，OH CY.A flexiblemulti-body dynamic model for analyzing the hysteretic characteristics and the dynamics stress of a taper leaf spring[J].JournalofMechanical Science and technology，2006，20(10)：1638-1645.

[11] KIM S，MOONW，YOO Y.An efficientmethod for calculating the nonlinear stiffness of progressivemulti-leaf springs[J].International Journal of Vehicle Design，2002，29(4)：403-421.

[12] SUGIYAMAA H，SHABANAA A A，OMARBM A，etal.Development of nonlinear elastic leaf springmodel formultibody vehicle systems[J].Computer Methods in Applied Mechanics and Engineering，2006，195：6925-6941.

[13] MOON ID，YOON H S，OH C Y.A flexiblemulti-body dynamic model for analyzing the hysteretic characteristics and the dynamics stress of a taper leaf spring[J].JournalofMechanical Science and Technology，2006，20(10)：1638-1645.

[14] ORTIZ G A，ALVAREZ D A，BEDOYA-RUIZ D.Identification of Bouc-Wen typemodels usingmulti-objective optimization algorithms[J].Computers and Structures，2013，114-115(1)：121-132.

[15] KANG DW，JUNG SW，NHOGH，et al.Application of boucwen model to frequency-dependent nonlinear hysteretic friction damper[J].Journal of Mechanical Science and Technology，2010，24(6)：1311-1317.

[16] WEN Y K.Method for random vibration of hysteretic systems[J].ASCE Journal of Engineering Mechanics Division，1976，102(2)：249-263.

[17] 鲁丽雪.Bouc-Wen土体动力本构模型及其阈值应变研究[D].大连：大连理工大学，2013.

[18] 陈欣，秦万军，蒋美华，等.钢板弹簧非线性刚度特性处理方法[J].军事交通学院学报，2014，16(1)：53-56.

[19] FANCHER P S，ERVIN R D，MACADAM CC，et al.Measurement and representation of themechanical properties of truck leaf springs[C].SAE Paper 800095.

[20] 孙涛，徐桂红，柴凌江.平稳随机激励路面模型的研究[J].汽车工程，2013，35(10)：868-872.

[21] 张立军，张天侠.车辆四轮相关路面非平稳随机输入通用时域模型[J].振动与冲击，2008，27(7)：75-78.