基于K-Means的特高频局部放电定位误差校正

张琛， 李孟东， 车瑶， 于彤， 方烈， 陈敬德

(1．国网北京市电力公司电力科学研究院，北京 100075;2.国网四川省电力公司内江供电公司，四川 641000;3．上海交通大学，上海 200240)

0 引 言

局部放电是电力设备绝缘缺陷的重要征兆，局部放电检测是避免绝缘击穿故障的必要手段。对局部放电源的定位，有助于提高检修效率，防止故障的进一步扩大。

当前可用的局部放电检测办法有脉冲电流法、特高频电磁波法、超声波检测法、化学检测法以及光学检测法等，其中特高频电磁波检测法和超声检测法是较为实用的方法[1-2]。近年来，基于特高频电磁波传感阵列的局部放电定位法因其具有定位范围广、灵敏度高且适合在线监测的特点，近些年引起了国内外学者的广泛关注，尤其在变电站局部放电站域定位方面具有非常好的推广应用潜力，时延估计准确是提高特高频法局放定位精度的关键，目前常见的时延估计算法有阈值法、相关估计法以及能量累积法[3-4]。然而这些方法都因自身的局限性而产生定位误差，理论分析和实验研究表明，对于特定的时延估计算法，由于白噪声、窄带周期性信号、脉冲信号等干扰，使得对同一放电源的定位结果具有明显的抖动特点。

K-Means聚类算法以距离作为相似性评价指标，即距离越近相似度越大，该算法最终将相似度最大的对象聚为一簇。本文提出的基于K-Means的特高频局部放电定位误差校正办法的核心思想就是对于同一测量点，记录多个定位数据，然后利用K-Means算法对这些定位数据进行聚类，选取簇中元素最多的簇的聚类中心作为本次最终的定位结果，实验表明，该方法对测量值具有很好的去抖动的作用。

1 基于TDOA的局放定位系统

该系统利用四路全向天线阵列采集局部放电辐射的电磁波，通过信号处理技术获得四元天线阵列分别接收到电磁波信号的时间差，通过数学运算即可得到放电源的空间位置。系统结构图如图1(a)所示，现假设四元传感器阵列布置在Z=0的平面上，四元传感器的位置坐标分别为S1(L1,L2,0)、S2(0,L2,0)、S3(0,0,0)、S4(L1,0,0)，某一时刻空间一局放源P(x,y,z)发出放电信号，该信号从发出到被S1接收所用的时间为t1，传感器S2、S3、S4接收到该信号比S1分别延迟t21、t31、t41，电磁波在空气中传播的速度为光速，用c表示，则可列如下三维空间定位关系式：

(1)

通过对方程组(1)进行加减消元运算可得：

(2)

则放电源的位置坐标可表示为：

(3)

其中θ为局放源在水平面上的方位角，r为局放源到传感器S1的距离。

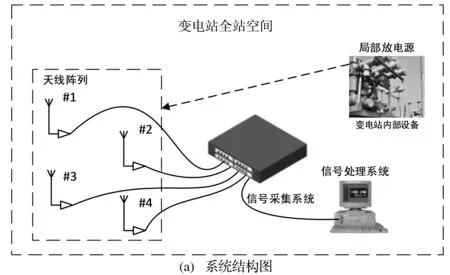
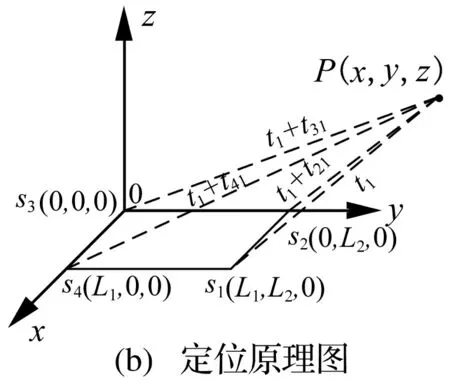
图1 特高频天线阵列局放定位示意图

观察式(2)(3)可知时延估计的准确度决定了定位的精度，而由于变电站现场环境复杂，噪声干扰信号较多，使得对同一放电点的定位坐标存在较大的波动，本文通过K-Means聚类算法找到对于同一放电源的不同测量值中的最可能的定位结果。

2 基于K-Means的测量值去抖动办法

在低信噪比(外界干扰信号较大)的电磁环境中，测量出的同一放电点的位置坐标存在波动，干扰了定位结果的选取，所以需要对测量值去抖动处理。

K-Means算法是划分方法中较经典的聚类算法之一。由于该算法的效率高，所以在对大规模数据进行聚类时被广泛应用[5-7]。K-Means算法以k为参数，把n个对象分成k个簇，使簇内具有较高的相似度，而簇间的相似度较低。K-Means算法的处理过程如下：首先，随机地选择k个对象，每个对象初始地代表了一个簇的平均值或中心;对剩余的每个对象，根据其与各簇中心的距离，将它赋给最近的簇;然后重新计算每个簇的平均值。这个过程不断重复，直到准则函数收敛。通常，采用平方误差准则，其定义如下：

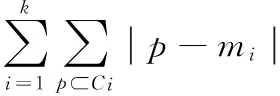
(4)

这里E是数据库中所有对象的平方误差的总和，p是空间中的点，mi是簇Ci的平均值。该目标函数使生成的簇尽可能紧凑独立，使用的距离度量是欧几里得距离。

本文采用K-Means聚类算法对测量值去抖动。在同一测量点，记录定位系统测量出的n个定位数据，运用K-Means聚类算法将这n个数据聚为m簇，假定ai为第i簇的元素个数，若

ai>aj,j≠i且j=1,2，…，m

(5)

则选第i簇的聚类中心为本次的测量值。

3 现场测试

为了验证本文所述方法的有效性，在上海某220 kV变电站进行了现场测试，测试系统的界面如图2所示。在方向角θ=90°和θ=160°方向上，径向距离r∈(5 m,50 m)范围内，以r的步长为5 m取标定点，作为放电源的放电位置，针对每个放电源得到25个位置测量值，图3散点图展示了θ=90°，r=6.5 m和θ=160°，r=21 m时，系统的定位结果和聚类情况。

由图3 可知，对于同一放电源，定位结果非常分散，如仅以一次测量值作为最终的定位结果，显然随机误差较大。依照本文的方法，选取聚类后的簇中元素数最多的簇的聚类中心作为最终定位结果，则对于放电源1(90°，6.5 m)，定位结果为圆形散点对应的簇的聚类中心(87°，8.6 m)，放电源2(160°，21 m)的定位结果为方块散点对应的簇的聚类中心(165.3°，27.6 m)。且通过实验可知，本文所述方法得到的定位结果具有稳定性，对于同一放电源多次测量的结果较为相近。

图2 车载式局部放电定位系统

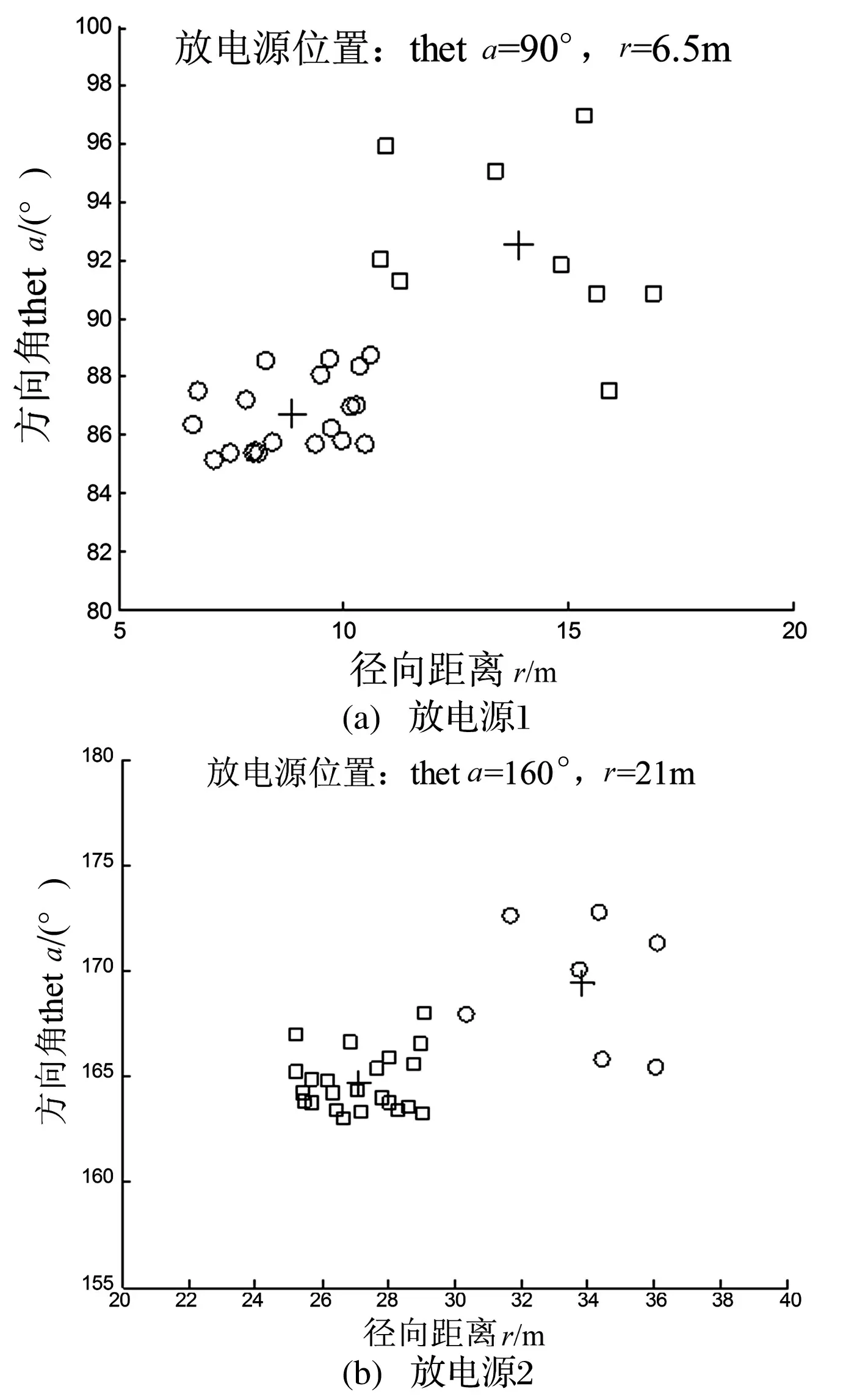
图3 系统的定位结果和聚类情况

图4给出了θ=0度方向上，r∈(5 m,50 m)范围内,一次测量结果误差分布情况和通过本文方法校正后的误差分布情况。可以看出，一次测量结果的误差分布具有较大的波动性，且误差值较大，通过本文方法校正之后，误差分布具有一定的规律性，且误差值整体较小。

4 结束语

本文针对基于特高频的局部放电定位方法的定位结果具有较大波动性的特点，提出了基于K-Means的测量值去抖动办法。实验结果表明，该方法能得到较为稳定的测量结果，且降低了定位误差，提高了测量精度，方法可行性较高。如何对定位误差进行有效补偿是本研究的后序工作内容。

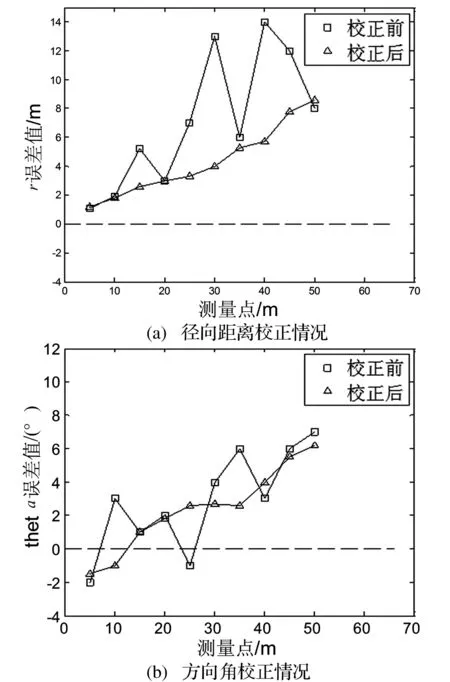
图4 校正前与校正后的误差分布情况比较

[1] 侯慧娟. 基于电磁波天线阵列的变电站局部放电信号处理及定位方法[D].上海：上海交通大学,2014.

[2] 侯慧娟,盛戈皞,苗培青,等. 基于超高频电磁波的变电站局部放电

空间定位[J]. 高电压技术,2012,38(6):1334-1340.

[3] 胡岳,王红斌,汤林,等. 基于UHF天线阵列的变电站局部放电全站监测研究与实践[J]. 电工技术学报,2014,29(Z1):502-509.

[4] 汤林,胡岳,王红斌,等. 基于插值相关法的局部放电特高频脉冲信号时延估计[J]. 高电压技术,2015,41(10):3320-3325.

[5] 赵莉,候兴哲,胡君,等. 基于改进k-means算法的海量智能用电数据分析[J]. 电网技术,2014,58(10):2715-2720.

[6] 吴夙慧,成颖,郑彦宁,等. K-means算法研究综述[J]. 现代图书情报技术,2011,32(5):28-35.

[7] 靖小平,彭小圣,姜伟,等. 基于K-Means聚类算法的自动图谱识别在电缆局部放电在线监测系统中的应用[J]. 高电压技术,2012,38(9):2437-2446.