基于不稳定周期轨道的参数扰动法在Boost变换器混沌控制中的应用

李姿

(华南理工大学 电力学院，广东 广州 510640)

李姿(华南理工大学 电力学院，广东 广州 510640)

0 引 言

电力电子变换器是一类典型的切换非线性系统，变换器的非线性动力学现象和建模得到了广泛的研究[1-3]。然而由于参数取值范围限制了变换器的工作区间，超出该区间，变换器中就会出现各种非线性动力学现象如分岔与混沌现象。这些非线性现象限制了变换器稳定工作的参数范围，并使变换器性能恶化，电压转换效率低[4-5]。因此，有必要利用混沌控制方法对处于混沌状态的DC-DC变换器施以控制，以提高变换器性能。

自 1990 年美国的 OGY 法[6]被提出以来，混沌控制的研究得到了蓬勃的发展，人们提出了各种控制方法[7-9]。文献[7]2-3最早尝试控制开关变换器中的混沌，利用OGY法对Boost变换器进行混沌控制，将处于混沌态的变换器稳定到预定的周期-1和周期-2轨道上。文章[10]1-3提出了对离散系统进行参数两步扰动的混沌控制方法，通过选取混沌吸引子中不稳定周期-1轨道(Unstable period orbit-1, UPO-1)为控制目标，以二维的Henon系统作为控制对象，在实际电路中验证了该控制方法的可行性。

故本文以DC-DC Boost变换器为研究对象，采用精确离散映射模型对其进行建模，选取UPO-1作为控制目标，并利用文献[10]1-2所述方法进行混沌控制。在不改变现有变换器拓扑及元件参数的前提下，充分利用变换器处于混沌态与多周期态时的动力学特征，使得处在混沌态或高周期态的变换器最终稳定到预定的目标轨道上。

1 Boost变换器的工作原理与非线性动力学行为简析

1.1 工作原理与建模

峰值电流模式控制Boost变换器如图1(a)所示，变换器在一个周期内存在两个不同的开关模式。当时钟信号来临时，触发器置位，开关管导通，电感电流iL上升，当其值上升至Iref时，触发器复位，开关管关断，D导通，电感L与电源E串联对负载提供电能，电感电流iL下降，直至下一时钟信号到来，如图1(b)所示。

图1 峰值电流模控制的Boost变换器

对于如图1所述的变换器，分别取电感电流iL和电容电压uC为状态变量，设第n个开关周期开始时刻，电感L电流iL和电容C电压uC初值分别为in，和un，建立电感电流连续模式下(Continuous Conduction Mode, CCM)的精确离散时间模型。

(1)

1.2 非线性动力学行为分析

选取周期T=100 μs，电感L=435.5 μH，负载电阻R=20.1 Ω，电容C=10.5 μF，输入电压E=5 V。作出如图2所示电感电流随参考电流Iref变化的分岔图，和对应的最大李雅普诺夫指数图。

图2 峰值电流模控制Boost变换器非线性动力学现象

在参考电流Iref由0 A增加到3.5 A的过程中，电流iL首先在参考电流为0.88 A时发生了倍周期分岔现象，系统由稳定的周期-1状态转变为周期-2状态，此时占空比d=0.37，电压增益G=1.55；然后运动轨迹与电流边界Ib=1.41 A发生碰撞，系统经边界碰撞分岔变为周期-4；此后，系统在经历了多次倍周期分岔之后与电感电流的边界条件发生碰撞，进入了混沌状态。

2 Boost变换器混沌控制参数计算

不稳定周期轨道的参数扰动法[10]1-2是一种适用于离散系统的混沌控制方法，通过对获取到的参数在平衡点附近加以扰动，可以实现在混沌系统中诸多不稳定周期轨道的选取并固定所需要的轨道。具体考虑两维离散系统，设状态变量为x，每个周期控制变量为pn，则可将在第n+1个周期和第n个周期的状态变量离散映射描述为：

xn+1=F(xn,pn)

(2)

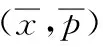
(3)

由线性近似表达式(3)可得：

(4)

当系统满足周期-1状态时，有：

(5)

可得到采用参数扰动法后，每个周期参数需要调整为：

(6)

取状态变量x=[iL,uC]T，选取参考电流作Iref为待扰动参数控制变量p。Iref=1.8 A时系统处于混沌状态，令xn=xn+1，可以求出混沌状态下的不稳定周期-1不动点：

(7)

由(3)式可得：

(8)

由此可得加入参数扰动混沌控制方法后，每周期参考电流需要调整为：

(9)

3 MATLAB仿真结果与分析

图3 加入控制前后电感电流、电容电压数值仿真波形图

对2.2节所述的参数扰动法控制的Boost变换器在MATLAB中进行数值仿真，所选参数与1.2中参数相同。可以得到如图3所示加入混沌控制前后电感L的电流iL波形图和电容C电压uC波形图。

从图3的时域图中可以看出，在未加扰动的情况下，在变换器处于混沌状态。0.05 s时参数扰动法开始作用，变换器最终能够稳定于原始混沌吸引子的不稳定周期-1轨道上。此时占空比为d=0.60，电压输出增益G=2.41，输出电压峰峰值为3.7 V，电感电流峰峰值为0.7 A，相比于混沌时的占空比d=0.37，电压增益G=1.55，输出电压峰峰值7.5 V，电感电流峰峰值1.6 A，电压增益有了明显提升，输出电压和电感电流纹波有了明显的下降。证明了基于不稳定周期轨道的参数扰动法的在Boost变换器中的混沌控制作用显著。

4 结束语

本文首先分析了Boost变换器中的非线性及混沌现象，并介绍了适用于离散系统的参数扰动法的原理。通过理论分析、数值仿真证实了基于不稳定周期轨道的参数扰动法在Boost变换器混

沌控制中的有效性。由本文研究可知，通过本文提出的混沌控制方案，可以扩大Boost变换器稳定工作的参数选取范围，提高电压转换效率，减小输出电压、电感电流纹波。本文的研究结果对DC-DC变换器的混沌控制，提升变换器性能的研究有着重要的应用价值。

[1] HMAILL D C,JEFFRIES D J. Subharmonics and chaos in a controlled switched-mode power converter[J] . IEEE.Trans.CAS. 1988, 35(8):1059-1061.

[2] 李春阳, 李冠林, 陈希有. 电流模式BOOST变换器倍周期分岔现象研究[J]. 电路与系统学报. 2013, 18(2):488-491.

[3] 石季英, 杨亮, 吴俊昭,等.软开关Boost变换器精确离散模型及其混沌现象[J].电气自动化, 2005, 27(2):24-26

[4] YANFENG CHEN, CHI K. TSE, SHUISHENG QIU, et al. Coexisting fast-scale and slow-scale instability in current-mode controlled DC/DC converters: analysis, simulation and experimental results[J]. IEEE Transactions on CAS-I, 2008, 55(10): 3335-3348.

[5] TEUVO SUNTIO.开关变换器动态特性: 建模、分析与控制[M].(许建平, 王金平译). 北京: 机械工业出版社, 2012.

[6] OTT E, CLESO GREBOGI,YORKE J A. Controlling chaos[J]. Physical Review Letters, 1990, 64(11):1196-1199.

[7] CHAKRABARTY K, BANERJEE S. Control of chaos in piecewise linear systems with switching nonlinearity [J]. Physics Letters A, 1995, 200(2):115-120.

[8] 罗晓曙,汪秉宏,陈关荣,等.DC-DC Buck变换器的分岔行为及混沌控制研究[J]. 物理学报, 2003,52(1):12-16.

[9] 周宇飞,陈军宁,谢智刚,等.参数共振微扰法在Boost变换器混沌控制中的实现及其优化[J].物理学报, 2004,53(11): 3676-3683.

[10] JIMENEZ TRIANA A, CHEN G, GAUTHIER A. A parameter-perturbation method for chaos control to stabilizing UPOs[J]. IEEE Transactions on CAS-II, 2015, 62(4): 407-411.