边攻击下的航线网络抗毁性测度
2018-01-11张豫翔吴明功温祥西王肖戎初洪帅
张豫翔, 吴明功, 温祥西, 王肖戎, 初洪帅
(1.空军工程大学空管领航学院,西安 710051; 2.中国人民解放军95949部队,河北 沧州 061736)
边攻击下的航线网络抗毁性测度
张豫翔1, 吴明功1, 温祥西1, 王肖戎1, 初洪帅2
(1.空军工程大学空管领航学院,西安 710051; 2.中国人民解放军95949部队,河北 沧州 061736)
针对航空网络的特定功能和特点,提出两个衡量航空网络抗毁性的新测度指标。以流量为边权(EW),基于网络吞吐量给出了网络的运输可靠性度量;基于节点之间联通情况,提出一种精确反映网络联通的可达性度量。最后,基于不完全信息攻击模型,提出两种攻击策略,对2个新指标进行仿真验证。实验分析表明:在EW攻击策略下,网络表现出较差的运输可靠性,运输可靠性随着信息获取量的增加下降更明显,但具有较强的可达性,而且随着信息获取度的增加反而有减缓下降趋势;UEB(Unweighted Edge Betweenness)攻击策略下,网络具有较好的运输可靠性和可达性,但对信息获取度反应不同,网络运输可靠性几乎不受信息获取量影响,而网络可达性的下降速度随着信息获取量的增加出现一定的加快趋势。提出的两个测度从不同角度反映了网络在不同攻击模式下的抗毁性,具有较好的测度能力,证明了测度指标的有效性。
航空网络; 加权网络; 网络抗毁性; 网络运输可靠性; 网络可达率
0 引言
航空网络运行的安全与否与国民经济、人民生活息息相关,因此对网络安全性进行研究具有重要的现实意义。基于复杂网络理论的抗毁性研究已成为一种有效的方法。网络抗毁性是指网络系统在遭受攻击、故障和意外事故时仍能够完成一定标准任务的能力[1]。近年来,基于复杂网络理论的网络抗毁性研究越来越受到关注。目前抗毁性研究的测度指标主要有平均路径长度、节点度、最大联通子图、网络效率等。很多研究都是基于无权网络[2-3],而现实网络往往都是有权网络,比如文献[2]中模型给出的风险效率指标的最短路径没有考虑不同节点之间的时间效益或者距离问题,因此无法准确反映实际网络的一些特征。航空网络是一个典型的节点连边网络,目前国内外针对航空系统进行了一定的研究[4-7],并证明了航空网络具有复杂网络的基本特性,但针对航空网络的抗毁性研究很少:文献[5]以最大联通子图为测度指标,对航空网络抗毁性进行了研究;文献[7]以网络全局效率作为抗毁性测度指标对美国抗毁性进行研究。这些研究还存在一些不足:1) 容量是衡量整个网络能力的一项重要因素,但目前的研究忽略了网络容量这个因素;2) 最大联通子图虽然能从总体上判断网络的联通程度,但无法精确衡量整个网络各个节点之间的联通程度;3) 选择的攻击方式过于单调,只有随机攻击和蓄意攻击,但很多时候攻击是在信息未知下进行的,因此有必要对研究航空网络在第3种攻击模式下的抗毁性。此外,目前的研究几乎都是针对节点失效,而现实网络在很多情况下还存在边失效,比如航路航线会受到天气或者军事训练等因素的影响。
因此,本文在现有抗毁性研究基础上,综合考虑现有评估模型的优缺点,针对基于航空流量的加权网络,将网络容量作为衡量抗毁性的一个基本切入点,提出航空网络可达性指标,根据网络节点对之间的联通状态提出网络可达性指标,较全面地考虑网络抗毁性的各个影响因素,构建测度函数,从而完善、健全航空网络的抗毁性测度。
1 不完全信息攻击模型
随机攻击与蓄意攻击是研究网络抗毁性的两种基本方式。随机攻击对应信息未知下的攻击,蓄意攻击对应攻击对象信息已知,但有时信息获取情况可能处于部分已知与部分未知之间。基于此,文献[8]提出了一种基于不等概率抽样的不完全信息条件下的攻击模型。

接下来用不等概率的抽样问题来选取目标量为n=N·f的边信息已知集。首先基于某个规则对边重要性进行排序,假设边e的排序号为ηi,在已知攻击信息广度参数f的情况下,取χi=ηi-δ为获取的边e的辅助参数,也是表示在该种排序规则下节点信息重要程度的参数,其中,δ∈[0,∞)表示该规则下节点重要度信息获取度,按照边e排序,其被获取的概率为

(1)
所有边重要度确定的情况下,δ越大获取的目标重要度信息越多,目标也越重要。
1) 当δ=0时,可得

(2)
所有边被攻击的概率相同,对应于随机攻击。
2) 当δ→∞时,有
(3)
假设η0是排序第一的边,即η0=1,当ηi=η0时有

(4)
当ηi≠η0时,有

(5)
即当δ→∞时,攻击目标是按照特定规则下边重要性选取的,即最重要的边首先被攻击,这与蓄意攻击相对应。
为了避免重要边重复入样,在攻击信息广度参数f确定的情况下,将边信息已知集的获取采取不放回抽样,过程如下:
1) 基于某种规则对网络边进行重要度排序,基于攻击概率选择第一个条边;
2) 基于同一个规则对剩余边重新进行排序,并计算其攻击概率;
3) 重复步骤1)、步骤2) 直至抽出攻击范围中的目标样本。
本文按照边权和无权边介数给出边重要性的排序,对应的攻击策略分别称之为EW(Edge Weight)攻击策略和UEB(Unweighted Edge Betweenness)攻击策略。根据排序选择边信息已知集Ω*,n=N·f是该集合的边数量。取某个时刻网络攻击的边数量m,采取如下攻击模式:
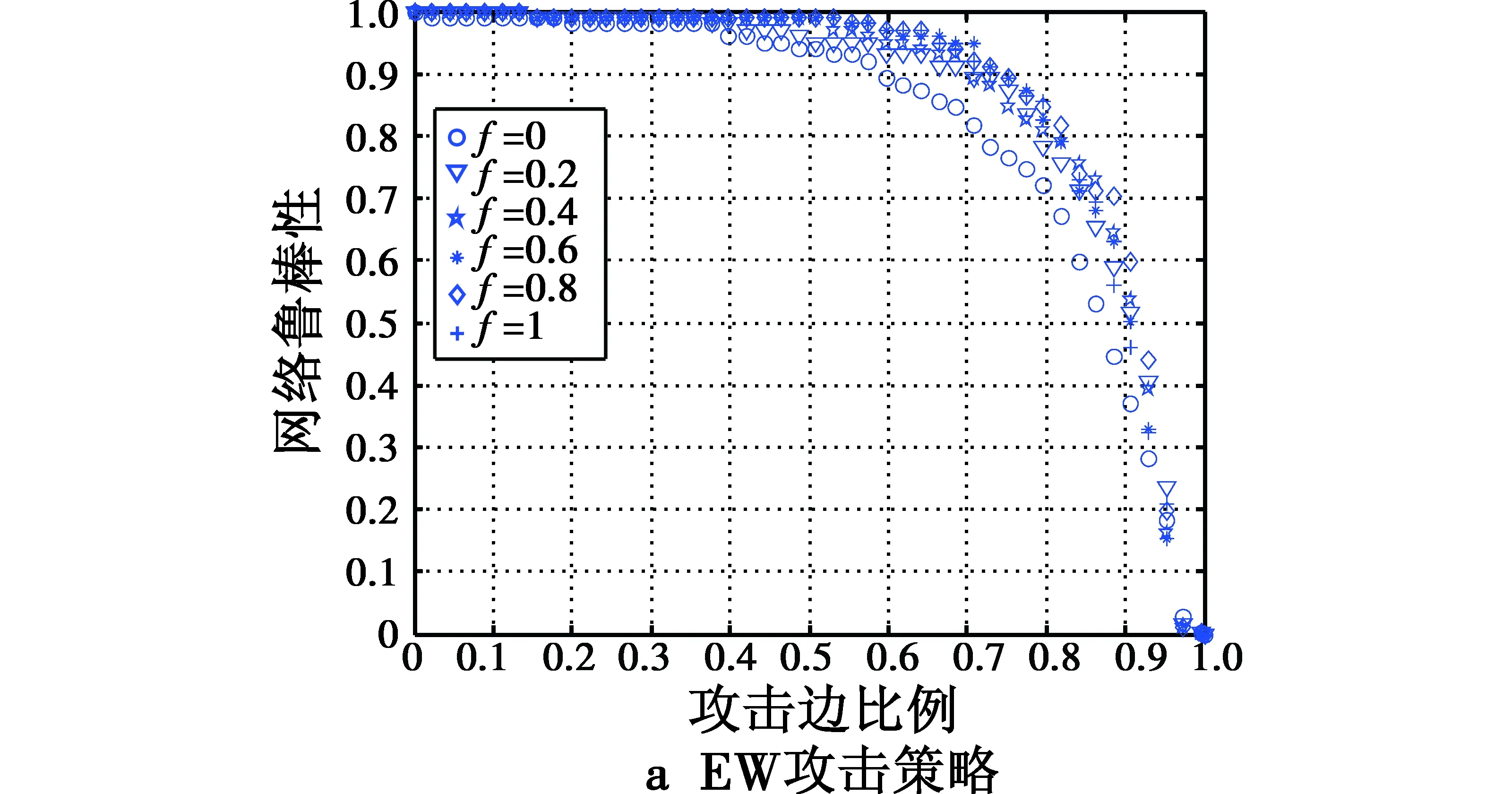
1) 当m 能否较准确地衡量航空网络在遭受攻击时的抗毁性,关键在于测度指标。因此,建立科学、全面的测度指标成为研究中的重要一环。航空网络抗毁性应该从网络的拓扑结构和物理功能两方面来测量。最大联通子图是从网络拓扑结构的角度来衡量网络的联通状态,主要从整体上研究网络的联通程度,对于衡量各个节点之间网络连通性则表现出了一定的局限性。如图1所示,节点A遭到攻击时网络断裂,此时网络的最大联通子图为虚框中的部分。 图1 最大联通子图Fig.1 Largest connected subgraph 从图中可以看出,最大联通子图中的连边数甚至没有剩余子图中的连边多。网络效率衡量的是网络的物理功能,反映网络的传输效率,但是没有反映网络的运输能力。基于此,本文充分考虑航空网络的拓扑结构和物理特性,以基于流量的加权网络为研究对象,给出网络的运输可靠性和可达性网络测度指标,反映网络吞吐量变化和节点对之间的联通情况,健全航空网络的抗毁性指标,从而更全面地掌握遭受攻击时的网络抗毁性。 为了简化模型,便于分析,本文做如下假设: 1) 网络中所有边只存在故障与正常两种状态,不存在除此之外第3种状态; 2) 边之间相互独立,一条边的失效不会导致其他节点和边的相继失效; 3) 航空网络为无向网络,因为机场之间相互往来的流量基本稳定,且流量相差很大的情况比较少。 网络可达性是指在正常工作情况下,网络遭到外部攻击时仍具有的传输能力。对于航空网络,最重要的任务就是完成旅客运输,这应是航空网络抗毁性必须考虑的方面,而网络的传输能力可以用整个网络的吞吐量来表示,在以往对航空网络的研究中,研究者几乎都忽略了这个重要因素。因此,本文用流量的损失情况来表示网络的运输可靠,当边失效时,该边上的流量全部剔除。 定义1 网络在边失效过程中网络损失情况。即 (6) 虽然学者们在可达性的精确定义方面仍然难以达成一致意见,但是普遍认定可将可达性的基本含义与个体在空间中移动的能力联系起来。针对常态情况下交通系统的可达性已有学者进行了研究[9-11],而非常态情况下网络可达性的评估方法与已有研究有些区别,提出的测度方法要能反映网络的受影响情况,通过对网络受影响程度的定量分析,测量网络的抗毁性。基于此,本文从不同的角度提出网络可达率指标ηA,即 (7) 式中:ηA的取值范围为[0,1];δij表示两节点之间的联通情况,即如果联通取值为1,否则为0。 为验证两个指标的有效性和实用性,本文对中国航空网络进行实证分析。数据来自于《从统计看民航2015》和互联网,其中,机场节点199个,连边2259条,以日平均飞行航班为权重,在数据处理时向上取整,网络为无向网络。 图2所示为重要度信息获取度δ为0时网络运输可靠性变化图。由于边权与网络运输可靠性相关,因此,获取的边信息越多,网络运输可靠性下降越快。由图可知,在EW攻击策略下,网络运输可靠性与信息获取量密切相关,在边信息已知的范围内攻击,网络运输量下降较快,而随机攻击下网络运输量下降比较均匀。攻击50%的边,信息获取量分别为0,40%,100%的情况下,网络运输可靠性分别为50%,40%,8%,说明信息获取度对网络的运输可靠性影响较大。而在UEB攻击策略下,信息获取量并不能影响网络运输可靠性的下降速度,下降速度与信息量并不存在明显关系,表现出较强的抗毁性。 图2 δ=0时网络运输可靠性Fig.2 Network reliability when δ=0 图3所示为δ→∞时网络运输可靠性变化图。与δ=0时相比,由于每次获取的都是最重要的边,因此网络运输可靠性下降更快,但在攻击信息未知边时网络运输可靠性下降相对缓慢得多。在EW攻击策略下,信息获取量为20%时,攻击20%的边,网络运输可靠性就下降至接近20%,当δ=0时这个数值为65%,δ的增加导致网络运输可靠性的急速下降。 图3 δ→∞时网络运输可靠性Fig.3 Network reliability when δ→∞ 图4所示为δ=0时网络可达性变化图。 图4 δ=0时网络可达性Fig.4 Network accessibility when δ=0 由图4可以看出,在EW和UEB攻击策略下,网络具有很强的运输可达性。在EW攻击策略下,无论边信息的获取度为多少,攻击边比例为80%时,网络仍有高达70%的节点连通。由于介数的特殊性,在UEB攻击策略下,随着信息获取量的增加,网络可达性呈加速下降的趋势,当攻击边比例为80%,边信息是小部分被获取时,网络的连通节点对数与EW攻击策略下的连通节点对数基本相同,仍有近70%。这种特性与中国的航空网络结构,即枢纽网络与点对点式网络兼容的特点是相吻合的,这也表明边权与边介数无明显关系。同时,在边信息被全部获取时,网络可达性表现出较快的下降速度,当攻击边比例为80%,网络连通节点对数只剩20%。 基于对δ=0时网络可达性的分析可预测,无论δ的取值多大,也不管信息获取量多大,只要在基于边权的边攻击策略下,网络均具有较强的鲁棒性,且随着信息获取量的增加,网络可达性不会出现加快下降现象,而且通过观察可得,当信息获取度很大时,鲁棒性的下降有减缓的趋势。 当δ→∞时网络可达性变化如图5所示。由图5可见,结果与上文的分析相一致。此外,对比不同δ可知,在UEB攻击策略下,随着δ变大,介数大的边被攻击的可能性也越大,导致网络可达性下降速度加快,在信息获取度增加的情况下尤其明显。 图5 δ→∞时网络可达性Fig.5 Network accessibility when δ→∞ 由仿真的结果可知,运输可靠性指标能较好地反映网络流量的变化情况,在不同攻击模式下能准确衡量网络整个吞吐量的变化趋势;可达率指标则能更精准地反映整个网络的联通状况,既能较好地表现出网络的性能变化,也能通过可达率指标来寻找网络中关键的连边,从而为保护网络性能提供参考。因此,本文提出的两个指标对于衡量网络的抗毁性具有较好的效果,证明模型的可靠、科学。 本文提出的模型也适用于基于节点的攻击,可作为另一个研究课题。由目前抗毁性研究现状可知,抗毁性测度指标比较多,那么如何寻找其中最关键指标,或者怎样将其综合考虑,这将是下一步工作的重点。 [1] ELLISON R J,FISHER D A,LINGER R C,et al.Survivable network systems:an emerging discipline,CMU/SEI-97-TR-013[R].Pittsburgh:Carnegie Mellon University,1997. [2] 种鹏云,帅斌.基于复杂网络的危险品运输网络抗毁性测度分析[J].中南大学学报:自然科学版,2014,45(5):1715-1721. [3] 李黎,管晓宏,赵千川,等.网络生存适应性的多目标评估[J].西安交通大学学报,2010,44(10):1-7. [4] ZHENG J F,GAO Z Y.A weighted network evolution with traffic flow[J].Physica:Statistical Mechanics and its Applications,2008,387(24):6177-6182. [5] 党亚茹,丁飞雅,高峰.我国航班流网络抗毁性实证分析[J].交通运输系统工程与信息,2012,12(6):177-185. [6] XU Z W,HARRISS R.Exploring the structure of the U.S.intercity passenger air transportation network:a weighted complex network approach[J].Geo Journal,2008,73:87-102. [7] 徐伟举.基于复杂网络理论的美国抗毁线路网络的抗毁性研究[D].成都:西南交通大学,2013. [8] 吴俊,谭跃进,邓宏钟,等.基于不等概率抽样的不完全信息条件下复杂网络抗毁性模型[J].系统工程理论与实践,2010,30(7):1207-1217. [9] GUTIERREZ J,GONZALEZ R,GOMEZ G.The European high-speed train network-predicted effects on accessibility patterns[J].Journal of Transport Geography,1996,4(4):227-238. [10] BOWEN J.Ariline hubs in southeast Asia:national economic development and nodal accessibility[J].Journal of Transport Geography,2000,8(1):25-41. [11] GUAN H Z,YIN Y F,YAN H,et al.Urban railway accessilibility[J].Tsinghua Science and Technology, 2007,12(2):192-197. Survivability Measurement for Airline Network Based on Edge Failure ZHANG Yu-xiang1, WU Ming-gong1, WEN Xiang-xi1, WANG Xiao-rong1, CHU Hong-shuai2 (1.College of Air Traffic Control and Navigation,Air Force Engineering University,Xi’an 710051,China; 2.No.95949 Unit of PLA,Cangzhou 061736,China) According to the specific functions and characteristics of airline network,two new measurements for network survivability were put forward.The transport reliability measurement was given based on network throughput taking the flow as the Edge Weight (EW).The accessibility measurement was proposed based on the link situation among nodes,which can accurately reflect the network connectivity.At last,simulation was carried out to verify the two proposed measurements by using two attack models based on incomplete information conditions.The result shows that:1) Under EW attack strategy,the network has a bad transport reliability,and the transport reliability decreases more quickly and obviously as the acquired information quantity increases;While the accessibility behaves well,and it shows a trend of slow descent as the acquired information quantity increases;and 2) Under Unweighted Edge Betweenness (UEB) attack strategy,the network has fine transport reliability and accessibility,but the response to the acquired information quantity is different:The transport reliability hardly changes as the acquired information quantity increases,while the accessibility has a certain acceleration of descent.Therefore,the two measurements can reflect the survivability under two attack strategies from two aspects,and have a good ability for measurement,which verifies the method. airline network; weighted network; network survivability; network transport reliability; network accessibility 张豫翔,吴明功,温祥西,等.边攻击下的航线网络抗毁性测度[J].电光与控制,2017,24(9):64-68.ZHANG Y X,WU M G,WEN X X,et al.Survivability measurement for airline network based on edge failure[J].Electronics Optics & Control,2017,24(9):64-68. 2016-09-09 2017-06-02 空管科研课题(GKG201410001) 张豫翔(1991 —),男,浙江金华人,硕士生,研究方向为空管运行与安全管理。 F59 A 10.3969/j.issn.1671-637X.2017.09.014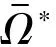
2 抗毁性测度指标

2.1 运输可靠性度量

2.2 可达性度量

3 航空网络仿真
3.1 运输可靠性




3.2 网络可达性



4 结论
