MEMS捷联惯导系统空中快速传递对准研究

任延超， 尹 文， 周建军， 刘 彪

(1.国防科学技术大学，长沙 410073； 2.中国兵器装备集团公司制导航空弹药研究开发中心，长沙 410100)

MEMS捷联惯导系统空中快速传递对准研究

任延超1,2， 尹 文2， 周建军2， 刘 彪2

(1.国防科学技术大学，长沙 410073； 2.中国兵器装备集团公司制导航空弹药研究开发中心，长沙 410100)

研究了一种MEMS捷联导航系统弹载条件下的快速传递对准方法,构建了速度+姿态匹配传递对准误差模型，提出了一种便于工程实时性应用的连续系统离散化方法。采用载机振翼机动方式提高方位角估计精度，同时针对MEMS器件零偏漂移大的问题，将陀螺残余零偏作为滤波器状态进行实时估计及补偿，并通过姿态、速度实时反馈修正，有效提高了传递对准精度。飞行试验结果表明，采用该方法导航系统60 s传递对准姿态精度优于0.15°，方位对准精度优于0.2°，达到了战术级武器的使用要求。

MEMS； 捷联惯导系统； 速度+姿态匹配； 传递对准； 反馈修正

0 引言

MEMS惯性器件由于具有体积小、重量轻、低功耗、低成本、高可靠性和耐冲击等独特优点，在惯性导航领域得到了广泛的应用。由MEMS惯性测量装置加卫星接收装置组成的捷联惯性/卫星组合导航系统，同时具备了惯性导航全天候及卫星导航高精度的优点，在高精度导航领域上具有极大的综合优势，使得低成本MEMS惯导应用于战术级武器[1]成为了当前的研究热点。 战术武器通常采用运动载体进行投放，其对导航系统的精度及准备快速性有较高的要求，因此,其导航系统的初始对准通常采用动基座传递对准方式完成，目前比较成熟的传递对准方法包括速度匹配、速度+姿态匹配[2]等。速度+姿态匹配传递对准算法[3]首先由KAIN J E和CLOUTIER J R于1989年提出，该算法能大幅缩短对准时间，提高姿态估计精度，同时降低了对准过程对载体机动的要求，是目前比较理想的传递对准算法之一。

MEMS惯性测量装置应用于航空制导炸弹将会是大势所趋，但MEMS器件零偏漂移大、零偏重复性差的缺点，会导致惯导系统产生巨大的非线性误差，使采用线性模型的传统卡尔曼滤波器发散。若采用实用EKF,UKF等适用于非线性模型的滤波方法，则会导致成本增加，对于我国旨在控制航空制导炸弹成本非常不利。

本文就MEMS陀螺零偏对对准滤波器的影响进行了分析，提出了一种适用于工程应用的速度+姿态匹配降阶滤波模型，采用滤波实时反馈校正及陀螺零偏在线估计补偿处理方法，实现了MEMS导航系统的高精度传递对准。

1 对准滤波器设计

1.1 滤波模型建立

设传递对准采用速度+姿态匹配Kalman滤波实现快速对准估计，滤波器的状态方程是子惯导的线性误差模型，通常采用导航误差及惯导测量误差建立系统误差模型构成滤波器状态向量，滤波状态向量为

(1)

式中：δpn为位置误差；δvn为速度误差；δφn为失准角；μn为变形角；εb为陀螺常值零偏；▽b为加速度计常值零偏；δKg为陀螺刻度系数误差；δKa为加速度计刻度系数误差。针对不同的应用环境，滤波器构建中也有加入反映主子惯导位置的杆臂系数、反映结构变形的颤振系数及反映主子惯导测量同步性的时间参数等状态量。滤波器状态越多，越能准确地描述实际系统的特性，但同时也带来负面影响:1) 滤波递推的计算量显著增加，设系统状态方程维数为n，观测方程维数为m，Kalman滤波计算量与n3+n2m成正比，状态量维数越多最终可能导致计算速度慢、累积误差严重，滤波发散；2) 状态量多，噪声数量就多，噪声统计特性就会变得非常复杂，准确模型的建立也越困难。

工程应用中，对滤波器的设计应综合考虑滤波模型的准确性及计算的经济性，建立系统的最优数学模型虽能最好地反映系统的真实物理特性，但完全准确的数学模型基本是无法找到的，因此建立合理的次优模型是系统设计的关键。以MEMS陀螺为例，陀螺误差一般数学模型为

δF=δK·ω+K·δω+δε+ν

(2)

式中：δK为刻度系数误差；K为训度系数；δω为角速率测量误差；ω为角速率；δε为零位误差；ν为输出噪声。刻度系数误差又包括重复性误差、非线性误差、不对称误差、温度敏感度等，零位误差又包括重复性误差、稳定性误差、随机游走系数、温度漂移误差等。如将陀螺、加速度计误差项均作为系统状态向量构建对准滤波器，其模型的复杂度及计算量以目前的嵌入式计算机将无法满足实际应用的实时性要求。

MEMS惯性器件一般在出厂前可以通过实验室或工厂设备进行精确标定[4]，大部份的确定性误差都可以补偿到较小误差，相对一般不超过数分钟的传递对准过程和制导炸弹飞行的工作过程，陀螺和加速度计的刻度系数误差及角速率漂移误差可看作微小量，对系统性能影响较小。器件的零位漂移将是其最大的随机误差，因此，在传递对准过程将陀螺和加速度计的零偏漂移误差作为状态向量进行估计，而将其余的误差简化为白噪声。陀螺和加速度计零偏误差模型可简化为

(3)

考虑炸弹通过挂架固定与载机刚性连接，主子惯导间物理安装关系可以事先标定，不考虑制造公差及各个设备的安装不精确等因素的影响，位置误差可通过杆臂参数进行补偿，通过系统状态可观性分析及机翼挠曲运动的影响，选定速度+姿态匹配方式实现弹载MEMS捷联导航系统的快速传递对准，MEMS捷联惯导系统误差模型为

(4)

滤波器状态方程为

(5)

选取2个速度误差(北向和东向)、3个失准角、3个变形角和3个陀螺等效零偏作为对准滤波器状态向量[5-6]，即

(6)

以陀螺、加速度计输出噪声及主子惯导角振动噪声为系统输入噪声向量w，即

(7)

(8)

状态转移矩阵F为

(9)

噪声转移矩阵G为

(10)

测量矩阵H为

(11)

1.2 滤波器离散化方法

根据上述建立的Kalman滤波器，其离散系统卡尔曼滤波方程[7]如下所述。

状态一步预测为

(12)

状态估计为

(13)

滤波增益矩阵为

(14)

一步预测误差方差矩阵为

(15)

估计误差方差矩阵为

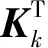
(16)

对连续系统进行离散化处理，重点需考虑状态转移矩阵的离散化和系统噪声的离散化，下面介绍一种便于工程应用的离散化方法，具体计算方法如下。

Φk,k-1计算方法。

在一个滤波周期T内，有n个导航计算周期ΔT(ΔT=T/n)，则有

(17)

式中，下标ki表示tk+iΔT时刻，且

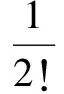
(18)

通常根据精度要求选取式(18)的计算阶次，本文选取一阶近似进行滤波器设计。

等效离散系统噪声方差阵Qk-1计算方法。

滤波计算中需要的系统噪声方差形式为Γk,k-1·Qk-1ΓTk,k-1，通常从连续系统GQGT直接计算Γk,k-1·Qk-1ΓTk,k-1，一般在一个滤波周期T内，将G看作常值，令Qk-1Γk,k-1Qk-1ΓTk,k-1，则有

(19)

2 针对MEMS器件的对准算法改进

2.1 MEMS陀螺零偏漂移补偿

传递对准滤波状态方程是捷联惯导系统线性误差方程，陀螺零偏较大时，由于姿态角不可交换误差和姿态误差一阶近似的原因，会引起系统实际误差偏离线性误差模型，造成非线性误差，导致滤波器发散。当陀螺零偏较大,并达到400 (°)/h时，造成的姿态非线性误差达到0.38°[8]。故将MEMS陀螺零偏作为滤波器状态向量进行实时估计，并将每一次残余零偏估计值用于对陀螺输出进行补偿，再参与对准及导航计算，从而减小陀螺零偏漂移对传递对准的影响。

在使用卡尔曼滤波器前，采用载机主惯导陀螺输出减去子惯导陀螺输出，时长30 min，得到子惯导陀螺零偏的初始估计值，作为陀螺零偏的初值进行传递对准滤波。子惯导零偏初始估计的计算方法为

(20)

式中:ε0为子惯导陀螺零偏粗估计值；ωi为子惯导陀螺输出减去主惯导陀螺输出值；N为数据采样总数；n为平滑数据个数。

2.2 状态实时反馈校正

由于采用速度+姿态匹配方式，姿态误差作为观测量进行估计，通过载机振翼机动飞行，主子惯导失准角具有良好的可观性，其状态估计能快速收敛，因此在每一次滤波周期内对子惯导速度、姿态和位置进行一次修正，再将状态向量残差作为新的状态量进行估计，只要滤波估计有效，每一次修正都可直接减少系统的误差，直至将系统误差控制在估计精度内。相比采用对准完成后进行一次输出校正，采用实时反馈方式因每进行一次滤波就对子惯导导航信息进行修正来减小系统误差，从而可以加快滤波器收敛，缩短对准时间，其原理如图1所示。

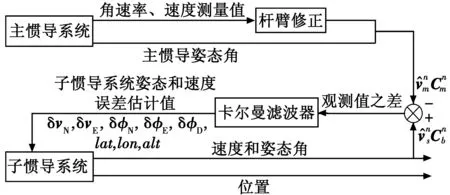
图1 滤波器反馈修正原理图Fig.1 The filter’s plan for feedback correcting

3 试验结果与分析

滤波器状态量初始方差矩阵P0为

P0=diag{(5 m/s)2,(5 m/s)2,(5°)2,(5°)2,(5°)2,(5°)2,(5°)2,(5°)2,(500 (°)/h)2,(500 (°)/h)2,(500 (°)/h)2}

(21)

系统状态量输入噪声方差矩阵Q为

Q=diag{(1×10-3g)2,(1×10-3g)2,(1×10-3g)2,(45 (°)/h)2,(45 (°)/h)2,(45 (°)/h)2,(0.05°)2,(0.05°)2,(0.05°)2}

(22)

系统观测噪声方差矩阵R为

R=diag{(0.1 m/s)2, (0.1 m/s)2,(0.05°)2,(0.05°)2,(0.05°)2}。

(23)

具体机动方式如图2所示。

状态估计滤波结果如图3所示。其中：φN,φE,φD为失准角估计值；ψN,ψE,ψD为变形角估计值；gx,gy,gz分别为x,y,z轴方向陀螺零偏。

从以上结果可以看出，采用滤波反馈校正方式，将滤波状态估计结果实时反馈至导航解算，动态失准角的误差在载机机动过程中迅速收敛至小角度，水平失准角估计方差为0.037 7°,优于0.15°，方位失准角估计方差为0.136 9°,优于0.2°，满足战术级制导武器快速对准的使用要求。

图2 飞行试验机动方式Fig.2 The maneuver manner of flight test

图3 飞行试验结果Fig.3 The result of flight test

4 结束语

设计了一种适于工程应用的MEMS捷联导航系统快速传递对准方法，飞行试验结果表明，采用该方法导航系统60 s传递对准姿态精度优于0.15°，方位对准精度优于0.2°，达到了战术级武器的使用要求。对低精度MEMS惯性器件在高精度战术级导航领域的应用研究具有较强的借鉴意义。

[1] 陈璞，雷宏杰.弹载捷联惯性制导系统传递对准技术试飞验证[J].中国惯性技术学报,2007,15(1):9-11.

[2] 刘斌，穆荣军，张新，等.两种快速传递对准方法在航空制导武器中的应用[J].中国惯性技术学报，2016,24(2):141-147.

[3] KAIN J E,CLOUTIER J R.Rapid transfer alignment for tactical weapon application[C]//Proceeding of AIAA Guidance,Navigation and Conference,1989:1290-1300.

[4] 陈来.捷联惯性导航系统动基座传递对准研究[D].哈尔滨： 哈尔滨工业大学,2007．

[5] LI W L,TANG K H,LU L Q,et al.Qptimization-based INS in-motion alignment approach for under-water vehicles[J].Optik Internationl Journal for Light and Electron Optics,2013,124(20):4581-4585．

[6] WU Y X,ZHANG H L,WU M P,et al.Observability of strapdown INS alignment:a global perspective[J].IEEE Transactions on Aerospace & Electronic Systems,2012,48(1):78-102.

[7] 付梦印，邓志红，闫莉萍.Kalman滤波理论及其在导航系统中的应用[M].2版.北京：科学出版社，2010：12-33.

[8] 孔星炜，郭美凤，董景新，等.大陀螺零偏条件下的快速传递对准算法[J].中国惯性技术学报,2008,16(5):509-517.

On Aerial Rapid Transfer Alignment of MEMS SINS

REN Yan-chao1,2, YIN Wen2, ZHOU Jian-jun2, LIU Biao2

(1. Mechatronics and Automation School,National University of Defense Technology,Changsha 410073,China; 2.Guided Airbomb Munition R&D Center,China South Industries Group Corporation,Changsha 410100,China)

A rapid transfer alignment method for missile MEMS SINS is presented.An error model of velocity+attitude information matching method is constructed,and a discretization way of continuous systems easy for engineering application is proposed.Through flutter maneuvering during the alignment procedure,the azimuth estimation accuracy is improved in the scheme.At the same time,in view of the large bias of MEMS inertial sensor,the residual zero offset of gyro is taken as the stage of filter for real-time estimation and compensation.The alignment precision is improved greatly through real-time feedback correcting of attitude and velocity.The flight test results show that the attitude accuracy is better than 0.15°,azimuth accuracy is better than 0.2°,and alignment time is less than 60 s,which can meet the tactical weapon requirements.

MEMS; SINS; velocity+attitude matching; transfer alignment; feedback correction

任延超,尹文,周建军,等.MEMS捷联惯导系统空中快速传递对准研究[J].电光与控制，2017，24(9)：23-26,30.REN Y C,YIN W,ZHOU J J,et al.On aerial rapid transfer alignment of MEMS SINS[J].Electronics Optics & Control,2017,24(9):23-26,30.

2016-08-22

2017-06-09

“十二五”装备预先研究项目(402030203)

任延超(1982 —),男，陕西户县人，学士，高工，研究方向为导航、制导与控制技术。

U666.1

A

10.3969/j.issn.1671-637X.2017.09.005