大失准角情形下UKF与CKF的比较研究

徐景硕, 王勇军, 刘 亚

(1.海军航空大学青岛校区，山东 青岛 266041； 2.中国人民解放军92514部队，山东 烟台 264007； 3.山东省产品质量检验研究院，济南 250102)

大失准角情形下UKF与CKF的比较研究

徐景硕1, 王勇军2, 刘 亚3

(1.海军航空大学青岛校区，山东 青岛 266041； 2.中国人民解放军92514部队，山东 烟台 264007； 3.山东省产品质量检验研究院，济南 250102)

扼要介绍了UKF和CKF滤波算法，分析总结了两种滤波算法的异同，并基于蒙特卡罗仿真试验，对大方位失准角情形下UKF滤波算法和CKF滤波算法的应用特性进行了对比、分析和总结，指出了UKF滤波算法对角运动和线运动均敏感，角运动和线运动方向的激励均可以加速其收敛，而CKF滤波算法对角运动不敏感，但对线运动敏感，角运动方向的激励无助于其对准精度的提高，而线运动方向的激励可加速其收敛，且收敛精度随激励效果的加强而提高的特性，为该种情形下对准技术的工程化实现提供了针对性建议。

UKF； CKF； 传递对准； 大方位失准角； 比较

0 引言

大方位失准角传递对准技术一直是惯性技术领域的研究热点和难点。由于大方位失准角条件下的传递对准模型是非线性的，从而非线性滤波算法的选取是实现传递对准技术的关键。理论上讲，非线性系统很难获得严格意义上的递推滤波算法。目前大都采用近似的研究手段，普遍采用的算法是高阶近似，涌现的滤波算法[1-5]主要集中在EKF，UKF和CKF上。由于EKF滤波算法是基于解析近似的方法近似非线性函数，一般适用于弱线性系统，而对强非线性系统，主要采取UKF滤波算法和CKF滤波算法，这两种算法是基于确定性采样来近似非线性系统的概率密度，通过不同的数学变换方法获得一定数量的采样点来逼近高斯分布的均值和方差。当然，粒子滤波(PF)也是不错的非线性滤波算法，但计算量大且存在粒子退化现象的不足在一定程度上限制了其在传递对准技术中的应用。

理论上看，UKF滤波算法和CKF滤波算法均是高斯假设条件下的贝叶斯估计，且从它们的泰勒展开式[4,6-8]中可知，UKF滤波算法具备泰勒级数展开二阶精度，而CKF滤波算法具备泰勒级数展开三阶精度。但在具体的实践应用上，尤其是在既有角运动又有线运动的摇摆基座情形下，UKF滤波算法和CKF滤波算法各自具备什么样的应用特性，对于选择哪种滤波算法实现大方位失准角传递对准而言至关重要。本文以大方位失准角条件下的捷联惯导系统为研究对象，对比介绍UKF滤波算法和CKF滤波算法的实现原理，归纳总结两者的异同，并基于蒙特卡罗样本试验，对大方位失准角情形下UKF滤波算法和CKF滤波算法的应用特性进行对比、归纳，为此种情形下对准技术的工程化实现提供选择建议。

1 UKF滤波算法和CKF滤波算法

UKF滤波算法于1995年首次问世，通过对非线性函数的UT变换选取采样点，实现对该非线性函数概率分布的近似。CKF(Cubature Kalman Filter)滤波算法于2009年由ARASARATNAM I和HAYKIN S提出，其主要思想是通过Spherical Radial 变换选取采样点，实现对该非线性函数概率分布的近似。为便于比较分析，考虑以下离散非线性系统

(1)

式中：f和h为非线性向量函数；Wk，Vk均为不相关的零均值高斯白噪声，其方差阵分别为Qk和Rk。

关于UKF滤波算法和CKF滤波算法的具体流程，文献[6-8]已有详细介绍，此处不再赘述。

1.1 UKF滤波算法和CKF滤波算法的相同点

针对同样的离散系统，根据UKF滤波算法和CKF滤波算法的工作原理和算法结构，两者具备以下几个相同点。

1) 从滤波方程看，两者均是高斯假设条件下的贝叶斯估计。

在假设系统噪声和量测噪声满足高斯分布的前提下，贝叶斯估计可简化为“非线性函数×高斯密度”形式的多维积分[9-10]求解问题，即

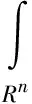
(2)

式中，f′(·)为被积函数。

上述积分很难解析求得，一般采取近似计算方法，即

(3)

式中：wi为权重系数；(wi,ξi)为权重点集。

非线性系统高斯假设条件下贝叶斯滤波方程的一般表达形式[11]为

(4)

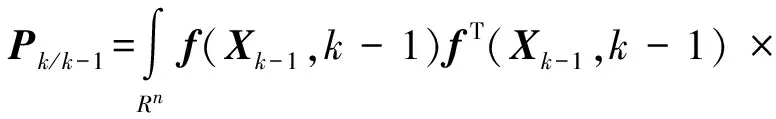
(5)

(6)

(7)

(8)

(9)

(10)

(11)

将UKF滤波算法和CKF滤波算法与式(4)～式(11)相比较可以看出，三者具备相同的表现形式，这说明UKF滤波算法和CKF滤波算法均是高斯假设条件下的贝叶斯估计。

2) 从点集上看，两者均是权重点集。

UKF滤波算法是通过UT变换的确定性采样产生Sigma权重点集，而CKF滤波算法是通过Spherical Cubature变换产生Cubature权重点集。

1.2 UKF滤波算法和CKF滤波算法的不同点

根据两者的运行机理，可得出UKF滤波算法与CKF滤波算法具有以下不同点。

1) 从计算量上看，UKF滤波算法计算量比CKF滤波算法的大。

每个滤波周期UKF滤波算法产生2n+1个Sigma点，而CKF滤波算法产生2n个Cubature点。

2) 从权重系数上看，CKF滤波算法的权重系数相同而UKF滤波算法的不同。

3) 从滤波精度上看，根据两者的泰勒展开式可知，UKF滤波算法具备泰勒级数展开二阶精度，而CKF滤波算法具备泰勒级数展开三阶精度，从而CKF滤波算法的滤波精度大多数比UKF滤波算法要高。文献[8]从理论上对UKF滤波算法和CKF滤波算法在使用场合上进行了研究，指出对三阶以下的低维非线性系统，由于UKF滤波算法精度比CKF滤波算法要高，一般选用UKF滤波算法。对于三阶非线性系统，两者的精度相当，但因为CKF滤波算法的计算量小，一般选用CKF滤波算法。对于三阶以上的非线性系统，由于CKF滤波算法的精度较UKF滤波算法要高，一般选用CKF滤波算法。

1.3 UKF滤波算法和CKF滤波算法的普适性

UKF滤波算法与CKF滤波算法均不具备普适性，即并不适用于所有的非线性系统。尤其当非线性系统中的量测方程在某个时刻关于状态估计值偶对称时，该系统无论是采用UKF滤波算法还是CKF滤波算法，均无法完成对系统被估计量的估计。下面具体说明。

假设一维非线性系统为

(12)

式中，系统噪声Wk-1和Vk量测噪声服从高斯分布。

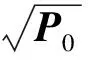
通过对UKF滤波算法和CKF滤波算法结构进行分析可知，之所以两者不能估计上述系统，原因在于该系统的量测方程关于状态初值偶对称。根据线性回归理论，若输入量关于初值偶对称，则会导致输入和输出不相关，继而导致相关系数为0，等同于滤波方程中的协方差阵为0，从而使得滤波增益为0，无法有效利用量测的修正作用实现对状态的正确估计。

2 大方位失准角非线性对准简化模型

2.1 坐标系定义

1) 载体坐标系(b系)，方向为右前上；2) 导航坐标系(n系)，采用东北天地理坐标系；3) 计算导航坐标系(n′系)。

2.2 大方位失准角非线性对准模型

根据捷联惯导系统的误差传播机理，结合文献[12]可推导出大方位失准角条件下捷联惯导系统非线性姿态误差方程和速度误差方程分别为

(13)

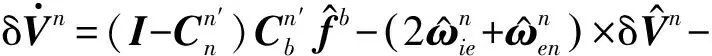
(14)

式中:

(15)

(16)

2.3 大方位失准角非线性对准模型简化

考虑到传递对准时间短，而短时间内是无法完成对陀螺零偏和加速度计零偏估计的，加之陀螺零偏和加速度计零偏量值小，对对准的影响小，且对准的核心是姿态失准角估计，为减少计算量，提高运算速度，在构建数学模型时可不必将其列入状态。

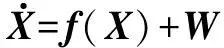
(17)

式中：

(18)

(19)

3 UKF滤波算法与CKF滤波算法在大方位失准角对准下的应用特性

线性的情况，一般采用UKF滤波算法和CKF滤波算法。下面以速度观测下姿态误差角的估计为例，通过蒙特卡罗仿真试验，研究这两种滤波算法在既有角运动又有线运动的摇摆环境下的应用特点。

摇摆环境选取平静、中等和恶劣3类海况，其参数设置[13]如表1所示。

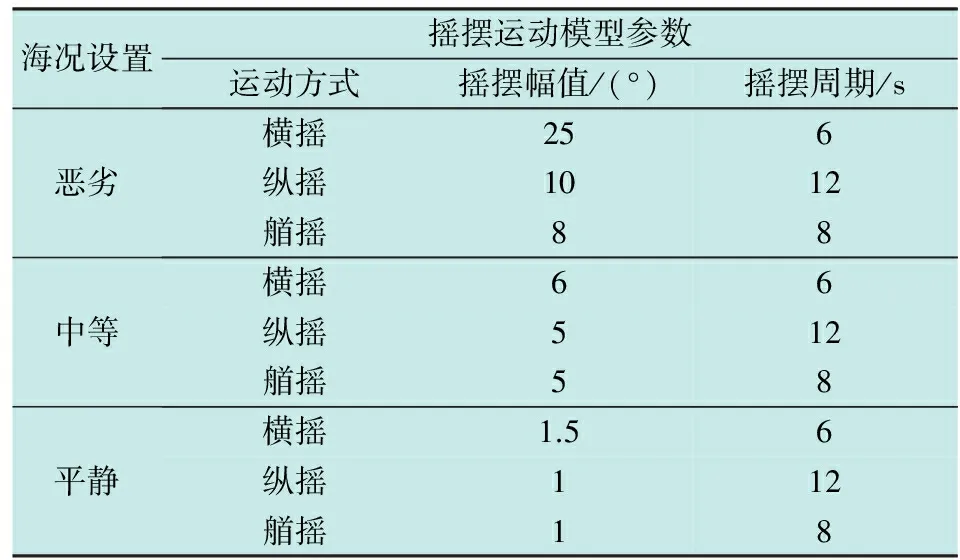
表1 不同海况参数设置

考虑以下9种仿真情形：情形1，静基座(无角运动，无线运动)；情形2，平静海况，无线运动；情形3，中等海况，无线运动；情形4，恶劣海况，无线运动；情形5，无角运动，有线运动(线加速度为0.5 m/s2)；情形6，无角运动，有线运动(线加速度为1 m/s2)；情形7，平静海况，有线运动(线加速度为1 m/s2)；情形8，中等海况，有线运动(线加速度为1 m/s2)；情形9，恶劣海况，有线运动(线加速度为1 m/s2)。

上述9种情形，每种情形进行20次仿真，并对姿态角误差取平均值绘制曲线，如图1所示。

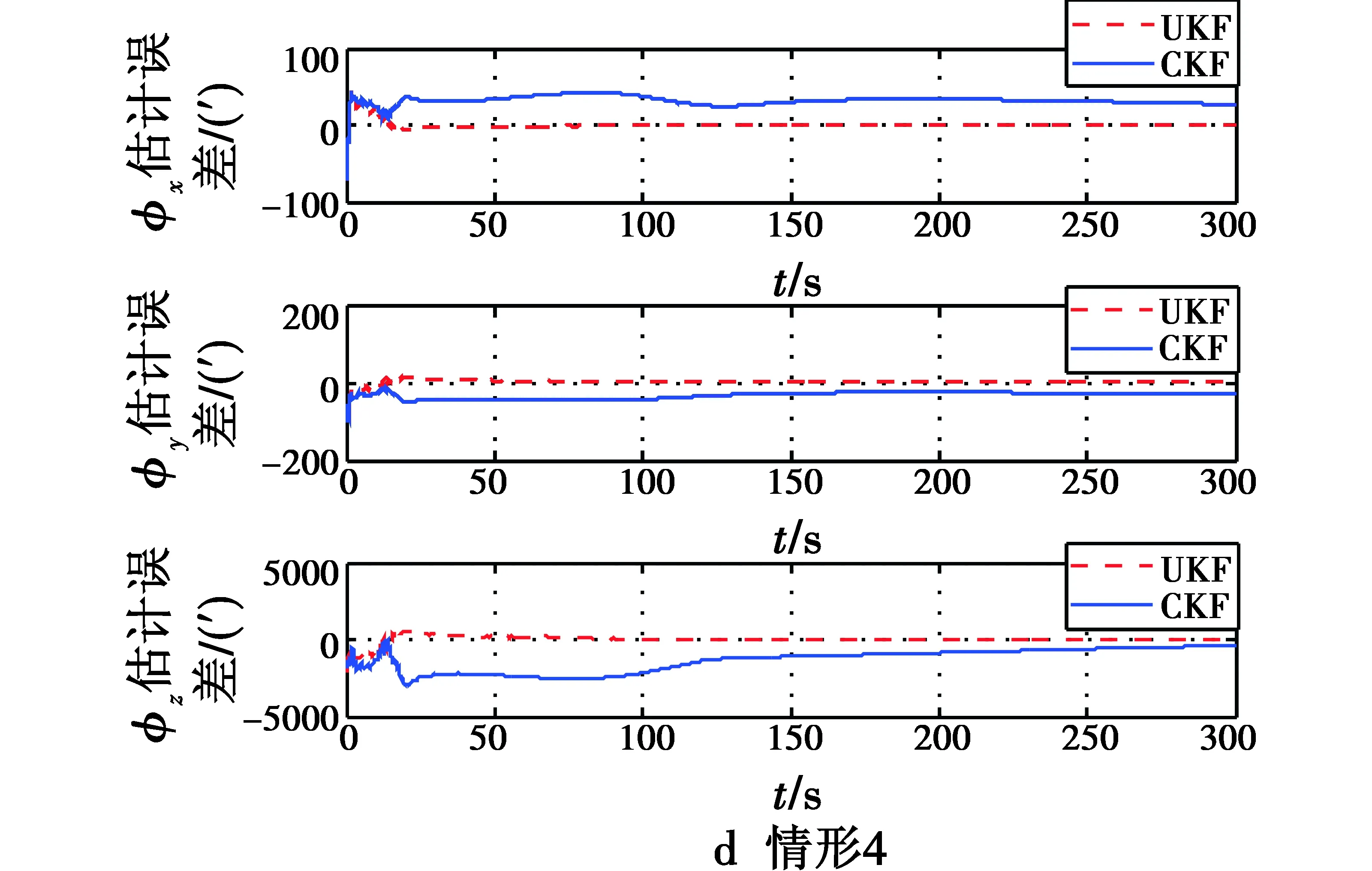
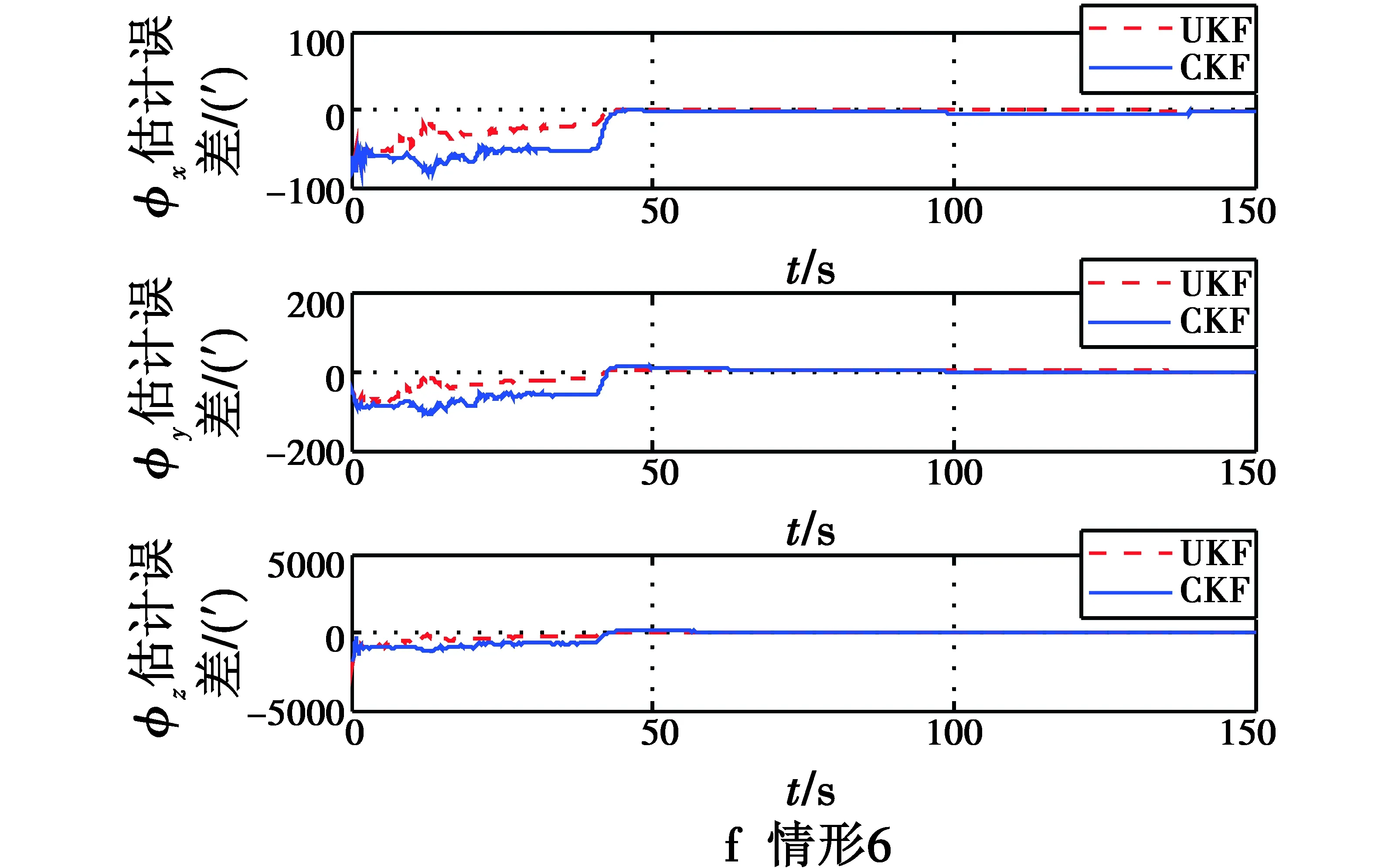
图1 9种情形下姿态角估计误差Fig.1 Estimated attitude errors of 9 cases

汇总上述9种情形的仿真结果，如表2所示。

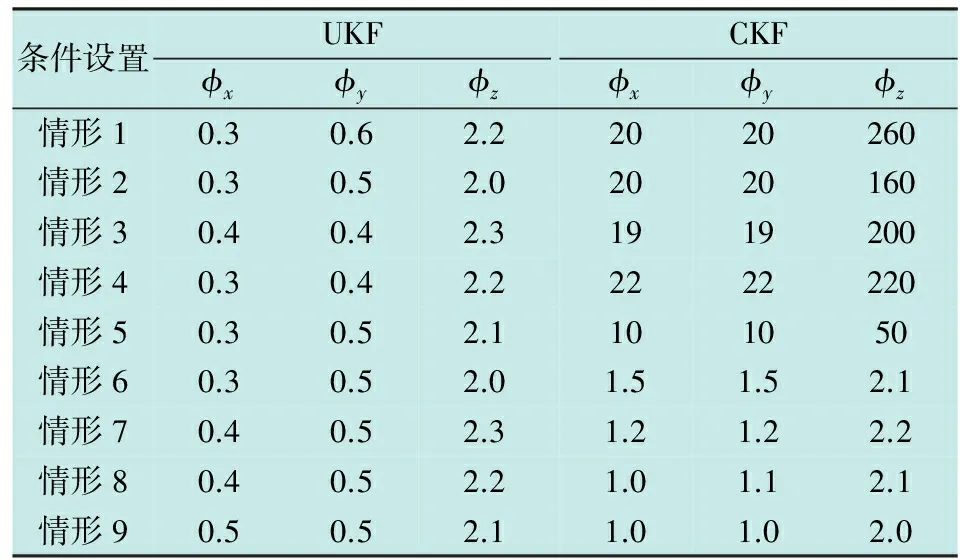
表2 9种情形的仿真结果

根据图1和表2归纳得出如下结论。

1) CKF滤波算法对角运动不敏感，但对线运动敏感，载体有线加速度时会加速CKF滤波算法的收敛，估计精度也会迅速提高。因此，利用CKF滤波算法实现大方位失准角对准只需载体具有线加速度即可，无需载体作角运动方向的激励。

2) 静基座或系泊状态因无线加速度，所以此时采用速度匹配利用CKF滤波算法虽能估计出姿态误差角误差，但因估计误差过大而无法实现大方位失准角对准。

3) UKF滤波算法对角运动和线运动都敏感，角运动或线运动方向激励的加强，有助其收敛，因此，无论是系泊还是航行状态，利用UKF滤波算法均可以较高精度估计出姿态误差角估计误差，实现大方位失准角对准。

4) 当载体有线加速度时，CKF滤波算法的估计精度会随线加速度变化的增加而提高，最终相当或略高于UKF滤波算法。

5) CKF滤波算法之所以对角运动不敏感，而对线运动敏感，原因在于其球形等权值采样策略，角运动的变化对球形的均匀分布改变不大，加之等权值的信息利用策略，不能加大对有效信息利用的权重，从而使得滤波效果不佳。

6) UKF滤波算法之所以对角运动和线运动均敏感，原因在于其UT变换确定性采样，按照不同权值进行信息分配，类似加权最小二乘估计，能有效完成对非线性函数的概率密度逼近，达到较好的滤波效果。

4 结论

UKF和CKF两种非线性滤波算法，主要通过确定性采样实现对非线性系统的概率密度的近似和逼近，从而实现对被估计量的估计。但两者均不具有普适性，不适用于所有的非线性系统，尤其是对于量测方程关于状态初值偶对称的非线性系统，故需根据系统非线性模型的实际情况进行选择。此外，由于UKF滤波算法与CKF滤波算法在构造采样点时采取的映射方法不同，决定其对角运动与线运动的敏感程度的不同。蒙特卡罗仿真验证结果表明，UKF滤波算法对角运动和线运动都敏感，角运动和线运动方向的激励均可加速其收敛，而CKF滤波算法对角运动不敏感，但对线运动敏感，角运动方向的激励无助于其对准精度的提高，而线运动方向的激励可加速其收敛，且收敛精度随激励效果的加强而提高，这个特性，对于大方位失准角条件下非线性滤波方法的选择和对准技术的工程化实现提出针对性建议。

[1] REID J G,TUCKER M,DAYAN R.An extended Kalman filter for the estimation of transfer alignment errors to an airborne vehicle[C]//AIAA Guidance Navigation and Control Conference，1980:54-61.

[2] HAO Y L，XIONG Z L,WANG W,et al.Rapid transfer alignment based on unscented Kalman filter[C]//Procee-dings of the American Control Conference,Minneapolis,2006:2215-2220.

[3] WANG Q,RIZOS C,LI Y,et al.Application of a Sigma-point Kalman filter for alignment of MEMS-IMU[C]//IEEE Position,Location and Navigation Symposium,2008:44-52.

[4] ARASARATNAM I.Cubature Kalman filtering:theory & applications[D].Hamilton:Mcmaster University,2009.

[5] ARASARATNAM I,HAYKIN S.Cubature Kalman filters [J].IEEE Transactions on Automatic Control,2009,54(6):1254-1269.

[6] 秦永元,张洪钺,汪叔华.卡尔曼滤波与组合导航原理 [M].2版.西安:西北工业大学出版社,2012.

[7] 孙枫,唐李军.Cubature卡尔曼滤波-卡尔曼滤波算法[J].控制与决策,2012,27(10):1561-1565.

[8] 孙枫,唐李军.Cubature卡尔曼滤波与Unscented卡尔曼滤波估计精度比较[J].控制与决策,2013,28(2):303-312.

[9] ITO K,XIONG K Q.Gaussian filters for nonlinear filtering problems[J].IEEE Transactions on Automatic Control, 2000,45(5):910-927.

[10] 伍宗伟,姚敏立,马红光，等.稀疏网格平方根求积分非线性滤波器[J].电子学报,2012,40(7):1298-1303.

[11] WU Y X,HU D,WU M P,et al.An numerical-integration perspective on Guassian filters[J].IEEE Transactions on Signal Processing,2006,54(8)：2910-2921.

[12] 严恭敏,严卫生,徐德民.简化UKF滤波在SINS大失准角初始对准中的应用[J].中国惯性技术学报,2008,16(3):253-264.

[13] 朱新颖,秦永元,杨鹏翔.舰载条件下一种新的传递对准方案与仿真研究[J].计算机测量与控制,2008,16(4):518-520.

Comparative Study on UKF and CKF in Large Azimuth Misalignment for SINS

XU Jing-shuo1, WANG Yong-jun2, LIU Ya3

(1.Qingdao Campus of Naval Aeronautical and Astronautical University,Qingdao 266041,China; 2.No.92514 Unit of PLA,Yantai 264007,China; 3.Shandong Institute for Product Quality Inspect,Ji’nan 250102,China)

The Unscented Kalman Filter (UKF) and Cubature Kalman Filter (CKF) are introduced,and ananalysis is made to their similarities and differences.Through Monte-Carlo simulation tests,the characteristics of UKF and CKF under large azimuth misalignment are studied,and the following conclusions are obtained:1) UKF is sensitive to both angular motion and linear motion,while CKF is only sensitive to linear motion;2) Both the incentive of angular motion and linear motion can speed up the convergence of UKF algorithm,but as to the CKF,the incentive of angular motion makes no contribution to the alignment accuracy while the incentive of linear motion can speed up the algorithm convergence;and 3) The CKF algorithm accuracy can be gradually increased with the improvement of the incentive of linear motion.The unique characteristics are helpful for the engineering realization of alignment technology.

Unscented Kalman Filter (UKF); Cubature Kalman Filter (CKF); transfer alignment; large azimuth misalignment; comparison

徐景硕,王勇军,刘亚.大失准角情形下UKF与CKF的比较研究[J].电光与控制，2017，24(9)：42-46,99.XU J S,WANG Y J,LIU Y.Comparative study on UKF and CKF in large azimuth misalignment for SINS [J].Electronics Optics & Control,2017,24(9):42-46,99.

2016-09-19

2017-06-25

徐景硕(1965 —),男，山东五莲人，博士，教授，博导，研究方向为惯性技术。

U666.1

A

10.3969/j.issn.1671-637X.2017.09.009