探索规律，巧解问题

江苏省海门市万年初级中学 郁春燕

探索规律，巧解问题

江苏省海门市万年初级中学 郁春燕

规律探索题渐渐成为近年来中考的热点问题，主要考查学生的观察能力以及推理能力，通过给定的图示或者材料，需要学生寻找两个或者多个变量之间的关系，解决这类问题需要学生提高自己的观察能力，找到问题中的内在规律。

规律；数字；图形

规律探索题是中考中的必考题型，这类题型一般以选择题的形式出现，题型一般是给出一组具有特定关系的数字、式子、图形，需要学生通过观察分析找出其内在的规律，再对此规律进行归纳和总结，从而解决问题。

一、数字规律

寻找数字规律的题型一般是先给出一组数字，需要学生找出这些数字之间的关系，再根据这些关系来解决问题。下面的例题就是数字规律题的典型代表，通过本题的解题研究，学生对数字规律题也会有一个更好的理解。

例1 已知正整数m的三次幂可以分裂成若干个连续奇数的和，例如23=3+5，33=7+9+11，43=13+15+17+19，如果m3分裂后，其中有一个奇数是2013，那么m的值是（ ）

A.43 B.44 C.45 D.46

解析：对给出的例子进行观察，找出其中的内在规律，对于23=3+5，分裂之后得到的第一个数是：3=2×1+1；对于33=7+9+11，分裂之后得到的第一个数是：7=3×2×1；对于43=13+15+17+19，分裂之后得到的第一个数是：13=4×3+1，寻找其中的内在规律，可以发现分裂成的数都是奇数，而且第一个数是三次幂的底数与前一个数的乘积再加1，奇数的个数等于三次幂底数。因此，m3分裂后的第一个数是m（m-1）+1，共有m个奇数。由于45×（45-1）+1=1981，46×（46-1）+1=2071，所以第2013个奇数是底数为45的数立方分裂之后的一个奇数，即m=45，所以正确的答案为C。

点拨：解决本题的关键在于找到分裂之后的第一个奇数和三次幂底数的变化规律，找到相关的规律之后，问题自然能够迎刃而解。

二、图形规律

图形规律题一般是给出一组图形，这些图形有共同点也有不同点，这类问题主要考查学生的观察能力以及结合图形的推理能力，通过所给出的图形，从它们的不同中寻找共同点，可以通过下面的例题来一探究竟。

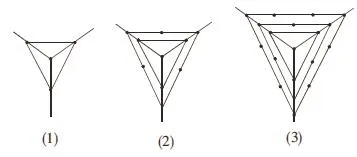
例2 观察右图中一组图形中点的个数，通过仔细观察，可以发现第一个图形中有4个点，第二个图形中一共有10个点，第三个图形中共有19个点，那么按照此规律，第5个图形中共有点的个数是（ ）

A.31 B.46 C.51 D.66

解析：对于第一张图，一共有4个点；对于第二张图，一共有10=4+6个点；对于第三张图，一共有19=4+6+9个点。根据此规律，可以推导出第n张图，一共有1+3×1+3×2+3×3+3×4+…那么本题中第5张图形中点的个数为所以正确的答案为B。

点拨：与图形有关的规律探索题一般比较简单，通过观察图形找到各个图形之间的内在联系，找到它们的共同点，本题通过前三个图形找到了这种图形的一般规律，从而快速解决问题。

三、函数规律

对于某些规律探索题，如果规律比较复杂，学生会感到无所适从，因此从函数的角度来思考问题就势在必行，通过函数的知识，可以建立相关变量之间的关系，通过变量之间的函数关系，问题的解决变得轻而易举。

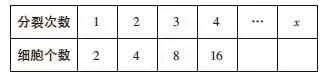
例3 某种细胞分裂时，由1个细胞分裂成2个，2个细胞分裂成4个，…，一个这样的细胞分裂x次之后，得到的细胞的个数为_____。

?

解析：对于此类问题，通过列表的方式，建立含有所有数据的表格，对于解题大有帮助，因此根据题意得到如上图所示的表格，根据表格可以发现：第一次分裂，得到的细胞个数为2=21；第二次分裂，得到的细胞个数为4=22；第三次分裂，得到的细胞个数为8=23；第四次分裂，得到的细胞个数为16=24……，可以猜想第x次分裂，得到的细胞个数为2x。

点拨：用函数的方法解决规律探讨题一般可以分成4个步骤，首先引入自变量和因变量，并画出表格填入x和y的对应值；接着根据变量关系，通过相关条件列出方程组；然后求出方程组的解，得到问题的规律；最后一步就是对所求的规律进行验证。

综上所述，规律探索题的解决需要遵循一定的方法，应该首先观察问题，发现问题的特点，接着探索问题中的规律，最后利用探索得到的规律解决问题。解决问题的方法说来容易，但是实际应用时也有一定难度，这就需要学生在平时的学习中勤加练习，认真总结和归纳。