高中数学解题策略分析——以高中的立体几何为例进行分析

山西省介休市第一中学 吴国婧

高中数学解题策略分析
——以高中的立体几何为例进行分析

山西省介休市第一中学 吴国婧

面对近年来愈来愈快速的教育改革，对于学生的要求也越来越高，以适应越来越严峻的高考形势。数学作为高中学习中极其重要的学科，在考试分数中占比较大，而且高中数学难度较大，如何学好高中数学，如何在解题的过程中寻求较好的解题策略，形成清晰的解题思路，显得尤为重要。本文将结合高中立体几何的解题思路来探讨总结如何面对高中数学中碰到的习题，寻求更好的解题策略。

高中数学；解题策略；立体几何

高中数学作为高中时期的一门重要学科，具有一定的学习难度，涉及的知识面广泛，综合性较强，对于学生的学习要求也相对较高，它不仅考验学生的基础知识积累，同时还在一定程度上考查了学生的逻辑推理能力，解题时，需要学生有清晰的解题思路和灵活的思维。立体几何作为高中数学中的重点难点，要求学生具有较强的空间想象能力和很好的记忆能力，本文将围绕该课题来详细介绍如何快速有效地完成解题。

一、培养有效的解题思路，需要牢牢掌握基础知识

“水之积也不厚，则其负大舟也无力。”对于任何一门学科来讲，方法的进步永远离不开坚实的基础。对于高中数学中公理公式繁多的立体几何问题来说，学生对于这些公式的理解与记忆就显得非常重要。那么在这个板块的学习中，需要学生做到的首先就是熟悉基本概念、定理以及各种推论，在理解的基础上去记忆，像一些平常使用频率高的公式公理，例如正弦定理、余弦定理、二面角公式等等，要做好记忆和运用。其次，自己课下要经常思考，总结各大定理和推论之间的联系与差异，明确每种定理和公式用在何种情况，一定要深入到每一个知识点，绝不放过每一个不起眼的地方，所谓“千里之堤，溃于蚁穴”，只有弄清楚每个细节，才能让自己的知识框架足够结实，面对难题时，才不会因为某一方面的不足而溃败。因为复杂来源于简单，最基础的东西堆积融合起来，可能就是一道比较难的题目，换个思路想，搞清弄懂了基础的东西，对于解决复杂的题目也会多一份支持。万变不离其宗，夯实基础，注重细节，能够为培养独特有效的解题思路提供坚实有力的支持。要想在数学学习和解题过程中取得进步，理解和掌握基础知识必不可少。

二、寻求有效的解题策略，需要仔细审题，注重动手能力，寻找突破点

对于一道题，在着手解答之前，要仔细地观察题目信息，明确题意是解题的重要步骤，也是核心所在，对于题目的理解程度直接决定了解题的速度与质量，但是大部分学生会忽略这一过程，导致解题过程中条理混乱，找不到正确的解题方向，这在考试中是非常致命的问题，会浪费大量宝贵的时间。所以，教师在解题策略的教学中，应当引导学生先仔细分析题目要求，把握题目所给出的信息，在其中寻找解题的突破口。例如下面这道立体几何题目：

已知正三棱锥P-ABC的底面边长为2a，点E、F、G、H分别是PA、PB、BC、AC的中点，则四边形EFGH的面积的取值范围是多少？对于这道题目，题干中没有给出相应的配图，首先学生要在题干中寻找有用的信息，绘出题目的立体几何模型，如下图：

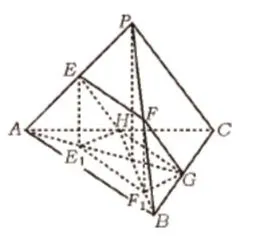
根据题目描述，通过作图很轻易地能够知道四边形EFGH为矩形，给解题过程带来了大大的便利，在题目中捕捉到的信息利用好，勤动手作图，会让解题的过程轻松有效。对于立体几何这一板块来说，辅助线显得尤为重要，在凌乱的思绪中，一条辅助线可能会带来一种“柳暗花明又一村”的感觉，一条恰到好处的辅助线会让解题过程事半功倍。至于怎样做好辅助线，需要学生对于题中信息进行分析，寻找其中的联系，根据题目的要求来发现需要什么样的辅助线才能达到目的。在明确目标的前提下多多动手，寻找题目的突破口，对于培养良好的解题思维有着重要的影响。

三、形成良好的解题习惯，需要多加磨练和反思改错

“熟能生巧，游刃有余”，任何良好有效的习惯和策略都离不开练习，尤其像数学这个学科，包含面广，只有通过不断地练习、总结，才能逐渐形成独特有效的解题思路，

在不断的解题过程中，能够及时发现自己的不足，从而巩固自己的薄弱环节。同样，错题也是学生学习过程中的重要财富，在错题中，学生能够不断推翻自己不正确的思路和想法，纠正自身在某些方面的误解，踏上解题的正轨。在解题和反思的过程中寻找解题的思路，完善自身的不足，有助于学生形成更加完备的解题策略，教师要大力鼓励学生参与其中。

想要学好数学，提高学生的解题能力，离不开练习与细心，教师要引导学生在解题时清醒地去完成每一个步骤，培养良好的解题习惯，总结解题规律，在不断地练习与总结中取得进步，找寻最适合自己的解题策略。

[1]魏华.高中数学解题策略分析——以高中的立体几何作为具体例子进行分析[J].神州（上旬刊），2012（10）：165.

[2]刘德贤.高中数学解题策略浅析[J].中国校外教育（上旬刊），2016（6）：14-14.

[3]刘海军.高中数学解题策略探讨[J].速读（上旬），2016（2）：186-186.