拨开迷雾,寻根溯源找模型——排列组合问题浅谈

■河南省商丘市第一高级中学 翟永恒

拨开迷雾,寻根溯源找模型
——排列组合问题浅谈

■河南省商丘市第一高级中学 翟永恒

排列和组合是高中数学的一个难点,同学们都知道这类题需要借助数学模型进行解决。但是有一些创新题情景生疏,如同雾里看花不知如何下手。其实这类问题往往蕴含着一些经典模型,只需要找到它们的“题根”,从而顺利转化为某些经典模型进行解题。

题根1：(拿贺卡模型)有4位同学每人写一张贺卡放在一起,然后每人拿一张贺卡,要求每人都不拿自己的贺卡,所有拿法总数是____。

解析：假设有甲、乙、丙、丁4人各写一张贺卡,甲先去拿一个贺卡,有3种方法,假设甲拿的是乙写的贺卡,接下来让乙去拿,乙此时也有3种方法,剩下两人中必定有一人自己写的贺卡还没有发出去,这样两人只有1种拿法,总的拿法为3×3×1×1=9(种),故答案为9。

例1 如图1,用四种不同颜色给图中的A,B,C,D,E,F六个点涂色,要求每个点涂一种颜色,且图中每条线段的两端涂不同的颜色,则不同的涂色方法种数共为( )。

A.2 8 8 B.2 6 4 C.2 4 0 D.1 6 8

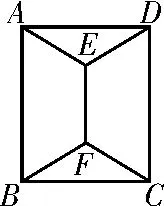
图1

例2 有4位同学在同一天的上午、下午参加“身高与体重”,“立定跳远”,“肺活量”,“握力”和“台阶”五个项目的测试,每位同学上午、下午各测试一个项目,且不重复。若上午不测“握力”项目,下午不测“台阶”项目。其余项目上午、下午都各测试一人,则不同的安排有____种(用数字作答)。

解析：先安排4位同学参加上午的“身高与体重”、“立定跳远”、“肺活量”、“台阶”测试,共有种不同的安排方法;接下来安排下午的“身高与体重”、“立定跳远”、“肺活量”、“握力”测试,假设A、B、C同学上午分别安排的是“身高与体重”、“立定跳远”、“肺活量”测试,若D同学选择“握力”测试,安排A、B、C同学分别交叉测试,有2种;若D同学选择“身高与体重”、“立定跳远”、“肺活量”测试中的1种,有种方式,安排A、B、C同学进行测试有3种。根据计数原理共有安排方式的种数为

题根2：(插空模型)有4名男生和2名女生站成一排,要求女生不相邻,则共有____种站队方法。

例3 在一次文艺演出中,需要给舞台上安装一排完全相同的彩灯1 5只,现以不同的亮灯方式来增加舞台效果,设计者按照每次亮灯时恰好有6只是关着的,且相邻的彩灯不能同时关掉,两端的彩灯必须要亮的要求进行设计,则不同的亮灯方式共有____种。

解析：问题实际只需要将9只亮的彩灯看作题根2中的男生,6个关的彩灯看作题根2中的女生,即可视为不相邻模型,由于两端的彩灯必须亮,所以共有=2 8(种)亮灯方法。

例4 显示屏上有一排共7个小孔,可显示0或1,若每次显示其中3个孔,但相邻的两个孔不能同时显示,则该显示屏能显示的信号种数为( )。

A.4 8 B.5 6 C.6 0 D.8 0

通过以上例题可以发现,虽然排列组合的问题情境不断推陈出新,乍一看可能无从下手,但仔细分析会发现实际上仍是经典模型的应用,我们只需追根溯源,即可顺利借助经典模型进行求解。

(责任编辑 王福华)