常用逻辑用语知识结构与拓展

■河南省南阳市第一中学 李 娜

常用逻辑用语知识结构与拓展

■河南省南阳市第一中学 李 娜

一、知识结构

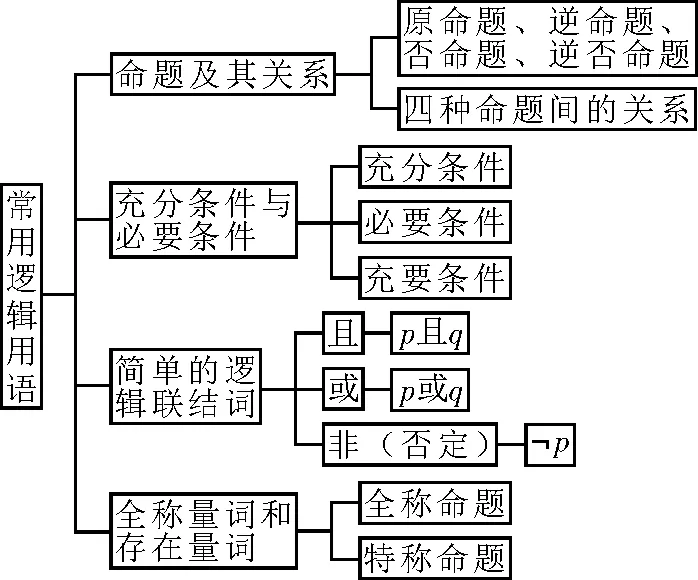
二、结构分析

高考考查常用逻辑用语的形式以选择题为主,试题多为中低档题目,命题的重点有三个:一是命题及其四种形式,主要考查命题的四种形式及命题的真假判断;二是以函数、数列、不等式及立体几何中的线面关系等为背景考查充要条件的判断;三是以逻辑联结词“或”“且”“非”为工具,考查函数、数列、立体几何、解析几何等知识。在复习时应重视充分条件、必要条件的判断,弄清四种命题间的关系,重视含逻辑联结词命题真假的判断,掌握特称命题、全称命题否定的含义,特别是应用转化与化归思想,利用原命题和其逆否命题的等价性,进行恰当转化,巧妙判断命题的真假。

三、典例分析

题型一：充分条件与必要条件

例1 设x>0,y∈R,则“x>y”是“x>|y|”的( )。

A.充要条件

B.充分而不必要条件

C.必要而不充分条件

D.既不充分也不必要条件

答案解析：当x=1,y=-2时,x>y,但x>|y|不成立;若x>|y|,因为|y|≥y,所以x>y。所以x>y是x>|y|的必要而不充分条件。

方法规律：充分条件、必要条件的几种判断方法:(1)定义法。直接判断“若p,则q”“若q,则p”的真假。(2)等价法。利用A⇒B与﹁B⇒﹁A;B⇒A与﹁A⇒﹁B;A⇔B与﹁B⇔﹁A的等价关系。(3)利用集合间的包含关系判断。设A={x|p(x)},B={x|q(x)},若A⊆B,则p是q的充分条件或q是p的必要条件;若A■B,则p是q的充分不必要条件;若A=B,则p是q的充要条件。

易错防范：判断条件之间的关系要注意条件之间关系的方向,正确理解“p的一个充分而不必要条件是q”等语言的含义。

题型二：四种命题

例2 有下列三个命题:①“若a>b,则a2>b2”的否命题;②“若x+y=0,则x,y互为相反数”的逆命题;③“若x2<4,则-2

答案解析：①原命题的否命题为“若a≤b,则a2≤b2”,错误。②原命题的逆命题为“若x,y互为相反数,则x+y=0”,正确。③原命题的逆否命题为“若x≥2或x≤-2,则x2≥4”,正确。故填②③。

方法规律：写出一个命题的逆命题、否命题及逆否命题的关键是分清原命题的条件和结论,然后按定义来写;在判断原命题的逆命题、否命题及逆否命题的真假时,要借助原命题与其逆否命题同真或同假,逆命题与否命题同真或同假来判定。

易错防范：正确区别命题的否定与否命题。“否命题”是对原命题“若p,则q”的条件和结论分别加以否定而得到的命题,既否定其条件,又否定其结论;“命题的否定”即“﹁p”,只否定命题p的结论。命题的否定与原命题的真假相反,即两者中有且只有一个为真。

题型三：全称命题、特称命题及逻辑联结词

例3 命题“∃x0∈(0,+∞),l nx0=x0-1”的否定是( )。

A.∀x∈(0,+∞),l nx≠x-1 B.∀x∉(0,+∞),l nx=x-1

C.∃x0∈(0,+∞),l nx0≠x0-1 D.∃x0∉(0,+∞),l nx0=x0-1

答案解析：改变原命题中的三个地方即可得其否定,∃改为∀,x0改为x,否定结论,即l nx≠x-1,故选A。

方法规律：(1)全称命题与特称命题的否定与命题的否定有一定的区别,否定全称命题和特称命题时,一是要改写量词,全称量词改写为存在量词,存在量词改写为全称量词;二是要否定结论,而一般命题的否定只需直接否定结论。(2)要判断一个特称命题是否为真命题,只要在限定的集合M中,找到一个x=x0,使p(x0)成立即可,否则这一特称命题就是假命题。(3)要判断一个全称命题是否为真命题,必须对限定的集合M中的每一个元素x,证明p(x)成立。只要找到一个反例,则该命题为假命题。(4)含有逻辑联结词的命题的真假判断口诀:p∨q→见真即真,p∧q→见假即假,p与﹁p→真假相反。

易错防范：(1)注意命题是全称命题还是特称命题,是正确写出命题的否定的前提。(2)注意命题所含的量词,对于量词隐含的命题要结合命题的含义显现量词,再进行否定。(3)由逻辑联结词构成的新命题的否定。①﹁(p∧q)⇔(﹁p)∨(﹁q);②﹁(p∨q)⇔(﹁p)∧(﹁p)。

四、跟踪练习

1.设有下面四个命题。p1:若复数z满足R,则z∈R;p2:若复数z满足z2∈R,

则z∈R;p3:若复数z1,z2满足z1z2∈R,则;p4:若复数z∈R,则¯z∈R。其中的真命题为( )。

A.p1,p3B.p1,p4

C.p2,p3D.p2,p4

2.命题“∀x∈R,∃n∈N*,使得n≥x2”的否定形式是( )。

A.∀x∈R,∃n∈N*,使得n

B.∀x∈R,∀n∈N*,使得n

C.∃x∈R,∃n∈N*,使得n

D.∃x∈R,∀n∈N*,使得n

解析：由于特称命题的否定形式是全称命题,全称命题的否定形式是特称命题,所以“∀x∈R,∃n∈N*,使得n≥x2”的否定形式为“∃x∈R,∀n∈N*,使得n

3.(2 0 1 7年长沙质检)已知下面四个命题:①“若x2-x=0,则x=0或x=1”的逆否命题为“x≠0且x≠1,则x2-x≠0”;②“x<1”是“x2-3x+2>0”的充分不必要条件;③“存在x0∈R,使得+x0+1<0”的否命题为“任意x∈R,都有x2+x+1≥0”;④若p且q为假命题,则p,q均为假命题。其中为真命题的是____。(填序号)

解析：①正确。②中,x2-3x+2>0⇒x>2或x<1,所以“x<1”是“x2-3x+2>0”的充分不必要条件,②正确。由于特称命题的否定为全称命题,所以③正确。若p且q为假命题,则p,q中至少有一个是假命题,所以④的推断不正确。故填①②③。

4.已知a>0,设命题p:函数y=ax在R上单调递减;命题q:设函数y=,函数 恒成立。若y>1p∧

q为假,p∨q为真,则a的取值范围是____。

解析：若p是真命题,则01。又ymin=2a,所以2a>1,所以q为真命题时。又p∨q为真,p∧q为假,所以p与q一真一假。若p真q假,则若p假q真,则a≥1。故a的取值范围为或a≥1。

(责任编辑 刘钟华)