高等数学微课程教学设计的研究

王 霞

（天津科技大学，天津300222）

高等数学微课程教学设计的研究

王 霞

（天津科技大学，天津300222）

阐述了高等数学微课程教学设计研究的意义。从高等数学教学内容的角度对概念及其相互之间的关系、公式、法则与定理、基本算法、知识点的总结及知识应用等进行微课程设计。设计理念是以学生为中心，将隐藏于知识背后的思想方法、数学文化法融入其中。目标是培养学生的各种思维能力，激发学生学习兴趣，提高高等数学教学质量与教学效率。

高等数学；微课程；教学设计

高等数学在普通高等院校课程中的重要性是不言而喻的，其教学效果的优劣将直接影响到人才培养的质量。在学分制培养模式下，高等数学的教学学时减少了许多。微课程是当今网络信息时代很重要的一种辅助教学手段，是在较短时间内（一般不超过15分钟）围绕某一高等数学教学内容或教学环节制作的微视频。

由于高等数学的内容是由概念、定理、公式和法则构成的逻辑体系，很适合微课程的短小精悍、主题明确、声情并茂、生动活泼、一课一个任务的特点。大学生课堂外有足够的时间对微课程教学资源进行预习、复习，弥补了由于数学难懂，没有教师指导看不懂的弊端，生动活泼的微课程资源充分调动了大学生的视觉、听觉和想象力，使他们不在感觉到数学的枯燥难学，而是给他们带来了全新的学习感受。

微课程辅助教学手段的使用，可以大大改善高等数学教学的现状，能够弥补传统课堂教学手段的不足，即弥补了传统高等数学课堂教学不直观、不形象和不生动以及课前、课中、课后互动教学和个别辅导不足的缺点，微课程的高等数学教学资源的声情并茂，能够激发学生的学习兴趣，使课堂教学变成有意义的活动，课堂效果得到了极大的提高，凸显学生学习的主体地位，能够增强大学生学习效率，有利于对学生进行因材施教，也不至于发生考试大面积不及格的现象，能够促进大学数学教师教学效率的提高及教学水平提升。

一、高等数学教学中重要概念的微课程教学设计

基本概念是高等数学教学的重要内容，为使学生真正理解并能运用概念解决实际问题，从概念产生与发展、几何直观解释、正确的数学语言表达、所蕴含的思想方法、具体求法及所体现的数学文化等角度进行微课程教学设计。

极限概念贯穿于高等数学教学的始终，既是教学的重点，又是教学的难点，其应用非常广泛，如渐近线、无穷小量、无穷大量、连续、间断、导数、微分、定积分、级数等概念都是由极限概念来定义的，使学生真正理解、掌握并会运用极限概念非常重要。因此，从六个方面对极限概念进行微课程教学设计。

1.极限概念的产生与发展

极限概念从古典的几何直观描述性的定义到现代精确的数学语言历经了几个世纪的演变，它的萌芽可以追溯到古希腊时期和我国战国时期，公元前3世纪，我国古代数学家刘徽在计算圆周率时建立的“割圆术”，用圆的内接正九十六边形的面积近似代替圆的面积，成功地将极限的思想进行了应用与实践，古希腊人的穷竭法同样也蕴含了极限的思想。在《庄子天下篇》中，有这样一句话：“一尺之棰，日取其半，万事不竭”，即数列在项数n无限增大的过程中，通项的值无限趋近于常数0这一现象。一句广告词语“没有最好，只有更好”道出了极限的真谛。

2.极限的直观描述性的定义

3.极限的ε-N数学定义

极限实质是一个数，是一个数列任意接近它，但总无法到达的数，其准确的数学语言是用加、减、乘及绝对值不等式将动态的极限过程用静态的算术语言表达出来。

4.极限概念所蕴含的思想方法

极限的研究过程中体现了最简单的思想，先研究数列极限，用类比的思想方法研究函数极限。从哲学角度看，极限概念体现出了常量与变量、有限与无限、近似与准确、特殊与一般、局部与整体、连续与离散、量变与质变，肯定与否定、直与曲、动与静的对立统一的辩证思想方法。

5.极限的具体求法

高等数学概念从计算的角度可以分为两类：一是只阐明概念的特性，而没有指明计算方法，极限概念就属于这一类，第二类本身指明计算方法，如导数的概念。极限的具体求法的微课程教学设计就是举出具体例子总结极限求法即可。

6.从文化角度对极限概念进行欣赏

极限是一条有尽头却走不到尽头的路，极限定义是数学中和谐美的典范：它同时出现无穷大和无穷小，即当n→∞（无穷大）时，，一对相互矛盾的对象统一起来，相互依存，何等和谐！极限方法把只能意会、不可言传的瞬时速度定义出来，再如李白的送《孟浩然之广陵》中“孤帆远影碧空尽，唯见长江天际流”的“孤帆”表达了趋于0的动态意境。

极限的人文精神是指虽然永远无法到达，而人们又不肯放弃的一种信念，给人一种神秘与无限想象的空间，人生中，每一点都是起点，也是终点，把每一点当作极限来追求，才是活出风采的王道。式子，表明积沙未必成塔，积土未必成山，如果每天积累太少，或者递减，逆水行舟，不进则退。

二、高等数学教学中公式、法则和定理的微课程教学设计

从挖掘与渗透数学思想方法、培养学生思维能力、以问题的形式等不同的角度进行微课程教学设计。

公式都是用有限来表示无限的，明确每个公式的实质，有利于学生灵活运用所学到的知识，如，实质是当分子是分母的导数时，这个积分就是分母以e为底的对数，即。

任何运算法则都蕴含着有大前提条件的思想，以极限的运算法则为例，在两个函数都有极限的前提条件下，他们的四则运算有极限，并且和（差、积与商）的极限等于极限的和（差、积与商），否则运算规则不成立，由于四则运算满足结合律，可将极限的和（差与积）的运算规则推广到有限多个，可以举出反例逆命题不成立，即规则看成定理时是充分条件，再叙述出规则的否命题及逆否命题，并举例说明是否正确，从而培养了学生严密的思维能力。

定理的微课程教学思路首先明确为什么要学这个定理，以罗尔定理为例，以问题的形式回答在讲罗尔定理之前为什么要讲费马引理？如何来理解罗尔中值定理的条件及结论？几何意义是什么？定理中的三个条件为什么是相互独立的？如果用第二条代替第一条定理的适用范围会发生什么变化？定理中的结论含义是什么？如何理解ξ的存在性？ξ的值是有限多个？还是无限多个？举例说明如何用罗尔的定理。

三、高等数学教学中基本算法的微课程教学设计

高等数学中涉及的计算较多，有些基本计算方法要求学生重点掌握，在进行微课程教学设计时注重引导学生掌握计算原则与计算方法。以不定积分第一换元法（凑微分法）为例，对教材的定理进行深入分析，给出一个清晰的数学语言表达算法：

该算法的重点是凑微分，由发散思维dx可以看成 1 与 dx 相乘，而，即凑系数再加适当的常数等，还有凑公式：， 凑法则：du±dv=d （u±v），vdu+udv＝d，将 3x8+1看成一个整体便可进行积分了。此题还可进行如下变形，由此题可启发学生做基本原理清楚了，只需做大量的练习就行了。

四、高等数学教学中知识点的归纳总结微课程教学设计

高等数学的知识模块较多，由于受教材编排体系的限制，没有将知识点进行系统的归纳总结，在进行微课程教学设计时，尽量将知识点编织成网加以归纳总结，以点带面，融会贯通。如变上限函数书上只给出了定理，其导数为被积函数本身，既然是函数，就应该将前面学过的知识联系起来，以例题的形式完成定义域的求法，函数值的计算，极限、导数与微分的算法等，特别是给出一般的求导公式，这样，学生比较容易理解变上限函数的概念。

五、高等数学教学应用知识的微课程教学设计

恒等变形、变量代换是高等数学解决实际问题最常用的方法，以不定积分的计算为例，说明恒等变形、变量代换方法是如何应用的。

设变量代换一：设t=x4，

设 x4=tant，dx4=dtant=sec2tdt，

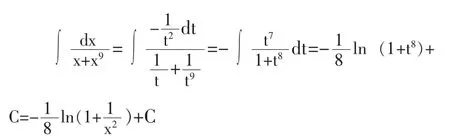
高等数学作为一门比较枯燥、难懂的课程，更需要微课程这样的辅助教学手段，通过文字、图像、语音等较为生动活泼的媒介，将知识资源整合和分类，在传递数学知识的同时，又能激发学生的学习积极性，并能培养学生的各种思维能力，从而达到提高教学质量和教学效率的目的。

[1]赵志成.高等数学课程中微课的设计与应用探析[J].教育观察，2017（11）：104-105.

[2]赵银善，懂海茵.高职院校高数微课程建设与思考[J].吉林工程技术师范学院学报，2016（6）：24-26.

[3]黄宽娜，刘徽.基于MOOC思想下的高等数学微课教学的设计与应用[J].西南师范学院学报（自然科学版），2016（10）：146-150.

[4]储亚伟，叶薇薇，王海坤.基于BOPPPS模型下的高等数学微课程教学设计[J].山东农业工程学院学报，2016（9）：153-156.

[5]段玉，王敬童.高等数学课程中若干难点的教学策略[J].当代教育理论与实践，2016（6）：61-63.

On the Teaching Design of Micro Course of Advanced Mathematics

WANG Xia
（Tianjin University of Science and Technology,Tianjin 300222,China）

This paperexpounds the significance of the research on the teaching deign of higher mathematics micro course.The micro course curriculum should include concepts,their mutual relations,formulas,rules and theorems,basic algorithm,key points and knowledge application.The design is students centered and integrates the ideas,methods and mathematical culture hidden in knowledge.The goal is to cultivate students’thinking abilities,stimulate their interests in learning,and improve the quality and efficiency of higher mathematics teaching.

advanced mathematics;micro course;teaching design

G642.0

王霞（1964—），女，教授，研究方向：基础数学。

天津市教育科学“十三五”规划重点课题（HE1020）。

张华凡）