双下侧二元混压式进气道不起动-再起动特性分析

杨玉新，陈 义，董新刚

(中国航天科技集团公司四院四十一所，西安 710025)

0 引言

进气道的起动/不起动状态是决定固体冲压发动机能否正常、稳定工作的关键。当超声速进气道处于不起动状态时，总压恢复系数和流量系数急剧下降，发动机推力降低；通常还伴随喘振，产生周期性热/力载荷，破坏进气道和发动机结构[1]。确定影响超声速进气道起动性能的因素，获得进气道起动/再起动特性，对提高进气道性能、扩大冲压发动机工作范围具有重要意义。

国内外对超声速进气道的起动/再起动问题进行了广泛而深入的研究。Ge-Cheng Zha等[2]通过数值仿真研究HSCT轴对称进气道在来流马赫数Ma=2下的流场后发现，喉道处流场的畸变程度对进气道起动性能影响很大。Saied Emami等[3]对来流马赫数Ma=4时，由于反压变化引起的超声速不起动/再起动过程进行了试验研究，得到了进气道能够再起动的收缩比范围，但目前公开资料中还没有给出详细数据。Mahoney[4]通过研究，给出了进气道面积收缩比、来流马赫数的关系对其再起动性能的影响。梁德旺等[5-6]研究了进气道内收缩比、飞行高度和攻角对超声速进气道起动性能的影响，还研究了典型超声速二元进气道不起动和再起动过程，发现通过增大来流马赫数使进气道再起动过程也存在迟滞回路现象。张堃元等[7-10]通过风洞实验和非定常数值仿真，研究了攻角动态变化对进气道起动特性的影响。然而，这些都是针对型面设计阶段的定几何进气道，没有考虑弹体和进气道布局形式对起动特性的影响。

本文针对某典型固冲发动机用双下侧布局二元混压式进气道的不起动-再起动特性，开展了高速风洞试验和弹体/进气道一体化数值仿真研究。通过试验获得了反压变化下进气道状态由起动-不起动-再起动过程；同时，建立了弹体/进气道一体化三维模型，通过数值仿真分析了双下侧布局形式的两个进气道在不同飞行状态下的流场特性，研究了飞行状态对不起动-再起动特性的影响。

1 风洞试验与数值仿真模型

1.1 物理模型

本文研究的典型固冲发动机进气道及其弹体如图1及图2所示，进气道几何型面中L=20.4Ht、H0=2.25Ht、H2=1.74Ht、δ2=1.75δ1、δ3=1.975δ1、δ4=2.5δ1。进气道为后置腹下90°双下侧气动布局方式，进气道与弹体间有隔道。自由流气体经过弹体预压缩，两进气道的三级外压缩面压缩后进入进气道内，经过转弯在圆形补燃室内掺混。该进气道工作马赫数范围为Ma=2.4～3.5，设计状态为Ma=3.0(攻角α=2°)。

试验模型后部与支撑机构相连，并通过节流锥调节进气道反压。图3为进气道模型在风洞中的照片。

1.2 数值仿真模型

数值模拟采用基于密度的隐式求解器，应用Roe-FDS矢通量分裂格式，控制方程离散选用一阶迎风格式。湍流模型选用标准k-ε模型，采用标准壁面函数。收敛准则为：残差至少下降3个数量级，且进气道出口截面流量稳定。

采用ICEM生成结构化网格，对近壁网格进行局部加密。在无侧滑工况下，弹体-进气道结构对称、流场对称，为节省计算量和时间，取1/2 的流场划分网格，网格数目约为144万。仿真侧滑角影响时对全流场划分网格，网格数目约为286万，图4给出了网格示意图。计算中采用的边界条件有压力远场、压力出口、无滑移固壁和对称边界条件(1/2计算域时)等。

1.3 数值仿真模型校验

为了验证本文所用数值计算模型正确性，根据文献[11]中德国亚琛工业大学的Herrmann等给出的进气道结构及超音速进气道内部压缩的试验研究结果，开展了相同工况下的数值仿真。

图5给出了本文数值模拟的马赫数分布图和试验纹影图对比，图6给出了本文数值模拟的壁面压力分布与试验结果对比。由图5及图6可看出，激波系结构非常吻合，压缩面和唇罩面压力分布也较吻合，FLUENT仿真结果很好地反映了激波在隔离段内的反射情况，准确预示了流动分离的位置。对比结果说明，本文选用的数值模拟算法和物理模型能较准确地模拟进气道的内外流场结构，计算结果可信度较高。

2 结果与分析

本文主要研究反压变化引起的进气道不起动-再起动过程，以及来流马赫数、攻角、侧滑角对进气道不起动再起动特性的影响。数值仿真工况范围为飞行高度H=10 km，来流马赫数分别为Ma=2.5～3.5、攻角α=-2°～8°、侧滑角β=0°～6°。风洞试验模拟了转级工况Ma=2.5、α=2°、β=0°条件下进气道不起动-再起动过程。下面对仿真和试验结果进行详细分析。

2.1 转级工况下进气道不起动-再起动性能

图7给出了Ma=2.5、α=2°、β=0°时不同反压下进气道对称面马赫数等值分布图。可看出，当出口反压等于来流静压时，进气道内流动全部为超声速，随着出口反压增大，扩张段内出现流动分离区，但主流依然是超声速流，进气道处于超临界状态；当出口反压等于11倍来流静压时，进气道喉道处出现结尾激波系，扩张段全部为亚声速流，且在扩张段内继续减速增压，进气道处于临界状态；当出口反压等于12.3倍来流静压时，结尾激波系稳定在进气道收敛通道后段，进气道处于稳定的亚临界状态。反压继续增加，结尾激波无法稳定在收缩通道内，将向上游移动到进气道唇口，如图7(e)所示。此时，无论维持或增大反压，结尾激波都将向上游移动，进气道进入不起动状态。文献[12]把结尾激波在进气道进口时的反压定义为“极限反压”。

进气道不起动后，考虑到发动机补燃室压力波动幅度可能较大，压力峰值会超过极限反压。因此，先计算了1.3倍极限反压下的流场，而后逐步降低反压，直至进气道再起动。

图8给出了进气道性能参数随反压变化，其中图8(a)为总压恢复系数，图8(b)为流量系数。从图8中可看出，进气道性能参数随反压变化曲线呈现明显的“迟滞环”变化，其中实线为进气道反压升高过程，反压升到极限反压pb=12.4p0之前，进气道都处于起动状态。虚线则为进气道反压降低过程，直至反压降到pb=6.6p0，进气道才能实现再起动。相同来流条件、相同反压下，在不同过程中的起动特性是不同的，这就是进气道起动的“迟滞环”现象。

图9为风洞试验中进气道在不同反压下的纹影照片。图9(a)为进气道的稳定亚临界状态，反压比达到最大pb=12.8p0，略高于数值计算的极限反压，表明进气道实际抗反压能力更强。节流锥继续前进，进气道进入不起动状态，如图9(b)所示，由于捕获的流量减少，反压比开始下降，降至pb=9.8p0，仍无法实现再起动。节流锥后退，反压比继续下降，唇口外的脱体激波被吞入，进气道再起动，随捕获流量增加，反压比迅速上升至pb=11.9p0，如图9(c)所示。

综上所述，数值计算结果与风洞试验结果吻合较好，表明由于反压变化引起的进气道不起动-再起动过程存在“迟滞环”现象。

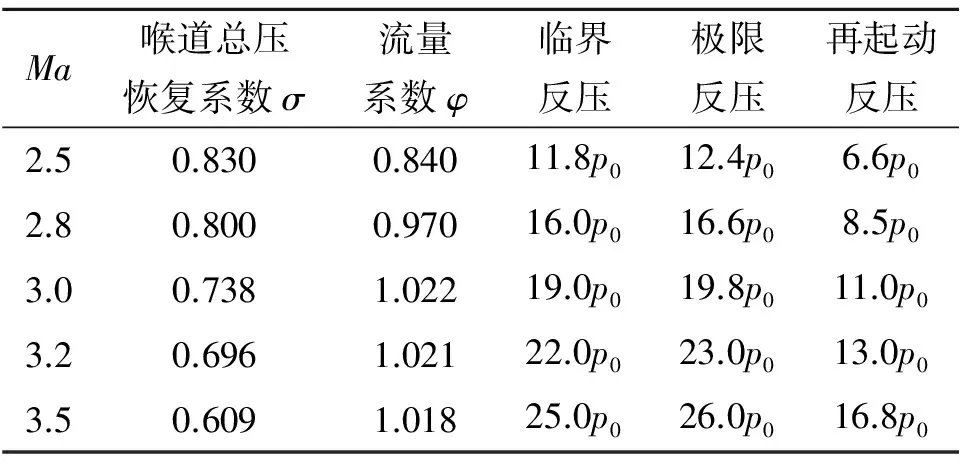
表1 不同马赫数下极限反压

2.2 来流马赫数对进气道不起动-再起动性能影响

表1 为α=2°、β=0°时不同马赫数下喉道总压恢复系数、流量系数、极限反压和再起动反压。可看出，在一定范围内，随来流马赫数增加，喉道总压恢复系数降低，流量系数先增加后不变，极限反压和再起动反压均升高，再起动反压接近极限反压的一半。

分析可知，来流马赫数越大，来流总压越高，但喉道总压恢复系数降低，两方面综合影响结果是喉道气流总压升高，气流抗反压能力增强。

2.3 攻角对进气道不起动-再起动性能影响

图10为Ma=3.0、β=0°时不同攻角下流量系数随反压变化曲线,图11为不同攻角下总压恢复系数随反压变化曲线。由图10、图11可看出，在本文研究范围内，进气道在正攻角下性能优于负攻角，且攻角越大，进气道性能越好，说明双下侧二元混压式进气道具有良好的正攻角性能。

表2为Ma=3.0、β=0°时不同攻角下极限反压和再起动反压。可看出，在本文研究范围内，攻角越大，喉道总压恢复系数和流量系数越大，极限反压越高。而再起动反压则是先增大、后基本不变。

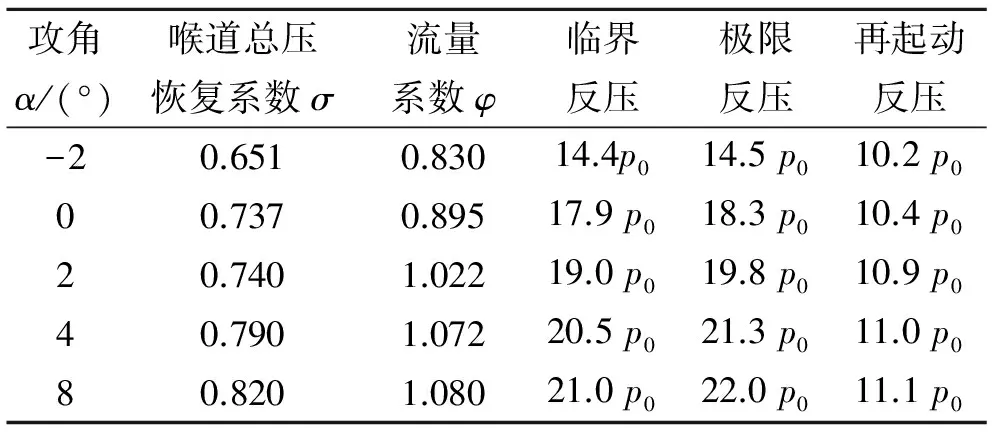
攻角α/(°)喉道总压恢复系数σ流量系数φ临界反压极限反压再起动反压-20．6510．83014．4p014．5p010．2p000．7370．89517．9p018．3p010．4p020．7401．02219．0p019．8p010．9p040．7901．07220．5p021．3p011．0p080．8201．08021．0p022．0p011．1p0

分析认为，对于构型一定的进气道，决定进气道再起动反压的主要因素是进气道进口前气流总压。当攻角α=-2°时，弹体对自由流预压缩作用较强，进气道进口前气流总压较低。因此，再起动反压较低。随着攻角增加，弹体的预压缩作用减弱，进气道进口前气流总压升高，进气道再起动反压也逐渐升高，当α≥2°时，弹体的预压缩作用已经相当弱。因此，进气道的再起动反压也将基本维持在11.0p0左右。

2.4 侧滑角对进气道不起动-再起动性能影响

侧滑角影响的仿真工况为Ma=3.0、α=2°、β=2°、4°、6°。侧滑角为正时，来流从弹体右侧(沿飞行方向观察)流向进气道，右侧进气道为迎风侧，左侧进气道为背风侧。

图12和图13分别给出了反压pb=16p0时背风侧和迎风侧进气道在不同侧滑角下进气道对称面马赫数分布图，从上到下依次为β=2°、β=4°、β=6°。由图可看出，迎风侧进气道分离包位置更靠近流场上游，说明迎风侧进气道抗反压能力低于背风侧进气道。

图14给出了β=4°时进气道性能参数随反压变化曲线。可明显看出，背风侧进气道的总压恢复系数、流量系数、出口马赫数均比迎风侧进气道高，背风侧进气道性能优于迎风侧进气道性能。

在β=2°工况下，当反压pb=18.7p0时，如图15所示，迎风侧进气道不起动，而背风侧进气道仍处在超临界状态，进气道系统处于单侧不起动状态。此时虽然背风侧进气道处于起动状态，但由于双下侧进气道的布局特点，背风侧进气道外压激波系受到迎风侧进气道弓形激波的干扰。仿真后发现，迎风侧进气道的弓形激波将破坏背风侧进气道外压激波系，使得背风侧进气道也进入不起动状态，如图16所示。

综上分析可知，在侧滑情况下，虽然两侧进气道流场特性和抗反压能力不同，但只要一侧进气道进入不起动状态，而反压又没用迅速降低，就会干扰另一侧进气道，使得两侧进气道都不起动。因此，本文将迎风侧进气道的极限反压定义为双下侧进气道的极限反压。

表3为Ma=3.0、α=2°时不同侧滑角下喉道总压恢复系数、流量系数和极限反压。其中，喉道总压恢复系数、流量系数均为迎风侧进气道的性能参数。可看出，在β=0°～6°范围内，随侧滑角增大，喉道总压恢复系数、流量系数均降低。因此，迎风侧进气道极限反压降低，双下侧进气道的极限反压降低。

表3 不同侧滑角下迎风侧极限反压

图17给出了Ma=3.0、α=2°、β=4°进气道性能参数随反压变化。

可看出，在侧滑情况下，反压变化引起的两侧进气道的不起动/再起动过程均存在“迟滞环”现象，但两侧进气道性能参数并不一致，再起动过程也不同步。在反压升高过程中，两侧进气道均处于起动状态，迎风侧进气道性能参数始终比背风侧进气道低，升到极限反压pb=17.0p0时，两侧进气道都进入不起动状态。在反压降低过程中，两侧进气道性能基本一致，降到pb=10.8p0背风侧进气道起动，但迎风侧进气道不起动，直至反压降到pb=8.7p0时，迎风侧进气道才启动。

表4 给出了Ma=3.0、α=2°时不同侧滑角下进气道极限反压和再起动反压。弹体侧滑角大于4°时，弹体对进气道流场影响变大，迎风侧流场比背风侧恶劣，因此，迎风侧进气道再起动明显滞后于背风侧进气道。在0°～6°范围内，随侧滑角增大，背风侧进气道再起动反压基本不变，迎风侧进气道再起动反压显著降低。

表4 不同侧滑角下极限反压和再起动反压

从表4 也可看出，进气道进口前气流总压是决定进气道再起动反压的主要因素。当弹体攻角α=2°，侧滑角变化时，背风侧进气道受弹体干扰较小，再起动反压基本不随侧滑角变化，维持在11.0p0左右。对于迎风侧进气道，当侧滑角β≤2°时，弹体干扰较小，再起动反压也接近11.0p0，当侧滑角β≥4°时，随侧滑角增大，弹体干扰增强，再起动反压逐渐降低。

3 结论

(1)由于反压变化引起的进气道不起动-再起动过程存在“迟滞环”现象。

(2)进气道极限反压与来流总压、进气道喉道总压恢复系数和流量系数相关。在本文研究范围内，随来流马赫数增加，自由流总压和流量系数均提高，喉道总压恢复系数降低，进气道抗反压能力增强。随攻角增大，进气道总压恢复系数和流量系数均提高，进气道抗反压能力增强。

(3)进气道入口前气流总压是决定进气道再起动反压的主要因素。来流马赫数越大，气流总压越高，再起动反压越高，与极限反压相比，降低35%～49%。攻角越大，弹体干扰越弱，入口前气流总压越高，再起动反压越高，α≥2°后弹体干扰极弱，再起动反压基本维持不变，与极限反压相比，降低30%～50%。

(4)在侧滑情况下，背风侧进气道抗反压能力强于迎风侧进气道。当迎风侧不起动后，迎风侧脱体激波干扰背风侧进气道的外压缩激波系，使背风侧进气道也进入不起动状态。

(5)在侧滑情况下，两侧进气道再起动不同步。背风侧进气道受弹体干扰小，再起动反压基本不随侧滑角变化，与极限反压相比，降低41.7%～49.87%；对于迎风侧进气道，随侧滑角增大，弹体干扰增强，再起动反压低于背风侧进气道，与极限反压相比，降低34.5%～44.4%。

[1] Takasaki S,Churchill B J,Fujimoto A,et al.Inlet unstart influence on aerodynamic characteristics of next-generation supersonic transport(SST)[J].SAE Transactions,1998,107:5546.

[2] Zha Ge-cheng ,Doyle Knight,Donald Smith.Numerical investigation of HSCT inlet unstart transient at angle of attack [R].AIAA 98-3583.

[3] Emami,Trexler A,Auslender H,et al.Experimental investigation of inlet combustor isolators for a dual mode scramjet at a Mach number of 4[R].NASA-TP-3502,1995.

[4] Mahoney J J.Inlets for supersonic missiles[M].Washingten: AIAA Education Series,1990.

[5] 梁德旺,袁化成,张晓嘉.影响高超声速进气道起动能力的因素分析[J].宇航学报,2006,27(4)：714-719.

[6] 袁化成,梁德旺.高超声速进气道再起动特性分析[J].推进技术,2006,27(5)：390-393.

[7] 郭斌.攻角动态变化对高超进气道性能影响研究[D].南京：南京航空航天大学,2009.

[8] 郭斌,张堃元.侧压式进气道攻角动态变化对其起动特性影响的风洞试验研究[C]//第一届高超声速科技学术会议.云南丽江,2008.

[9] 郭斌,张堃元.攻角动态变化的侧压式进气道风洞实验[J].航空动力学报,2009,24(7)：1601-1605.

[10] 刘凯礼,张堃元.迎角动态变化对二元高超声速进气道气动特性的影响[J].航空学报,2010,31(4)：709-714.

[11] Herrmann C D,Koschel W W.Experimental investigation of the internal compression of a hypersonic intake[R].AIAA 2002-410.

[12] Van Wie D M,Kwok F T,Walsh R F.Starting characteristics of supersonic inlets[R].AIAA 96-2914.