让几何概念教学多一些动态处理

尤丽芳

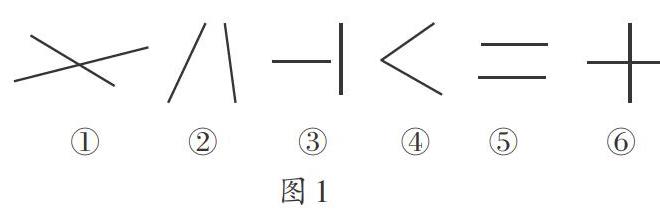
[摘 要]让学生精准理解几何概念的内涵，发展空间观念，是小学几何教学的重点和难点。将动态的图形运动融入课堂教学，并通过动态的处理，让几何表征更加直观形象，以此帮助学生系统构建知识网络。

[关键词]几何概念；动态处理；空间观念

[中图分类号] G623.5 [文献标识码] A [文章编号] 1007-9068（2018）35-0039-02

如何让小学生精准深刻地理解几何图形的本质特征和空间关系，是几何教学的重点，也是难点。笔者认为，教师可将物体和图形运动融入课堂教学中，将静态的几何图形进行平移、旋转等动态处理，让学生获得直观的动态体验，从而有效把握几何图形之间的相互关系，促进学生空间观念的发展。笔者现从自己的教学实践出发，谈谈具体的做法和思考。

一、借助动态处理，显化概念本质

在学习几何图形时，学生以形象思维为主，容易被外部的显性特征所吸引，导致学习浮于表层，不能有效深入理解几何概念的本质。这就需要教师运用动态处理的方式，让概念内隐的本质特征显性化，从而帮助学生深刻理解概念的本质属性。

例如，“平行与垂直”一课的教学中，根据教材编排，教师通常会让学生先任意画出两条直线，然后通过观察和分类得出结论，并最终总结出“平行”的概念。这样的教学，学生虽然能够熟练记住平行的概念，但是面对“两条直线相交，但还没有交叉”这个情况，往往会产生误判。到底为什么会这样呢？笔者认为，问题的症结在于，学生没有深入理解“平行线之间的距离处处相等”这个本质属性。为此，笔者从动态处理的视角展开了三个层次的教学。

层次一，呈现动态素材，引导学生展开想象。

笔者引导学生对图形的平移和旋转进行回顾和复习，并展开动态的空间想象：1.格子图上有一条直线向上做平移运动然后停下来，想一想这条直线前后的位置关系是怎么样的？2.格子图上的一条直线绕着线上的某一个点不停地旋转后停下，想一想这条直线前后的位置关系又会是怎么样的？

在这个动态过程中，学生展开空间想象，不但积累了活动经验，而且借助图形运动有效感知平面内两条直线的空间关系，从而促进空间想象能力的发展。

层次二，进行经验迁移，挖掘知识本质。

笔者先让学生根据自己的想象，画出两条直线的位置关系，然后让学生根据所画作品（如图1）展开交流和探讨：

哪些是通过图形的平移得到的？哪些是通过图形的旋转得到的？通过旋转得到的两条直线和通过平移得到的两条直线的位置关系有什么不同？为什么？学生经讨论后认为，通过旋转得到的两条直线会相交，而通过平移得到的两条直线，因为直线上的每一个点都平移了，所以每一处对应点的距离都相等，因此不会相交。

层次三，展开动态操作，内化概念。

当学生对“平行”的概念有了一定的认识之后，笔者让学生画平行线。通过动态操作，学生体验“平移→平行→平移”的动态过程，能够透过平移这个动态的生活现象，理解平行概念的本质特征，然后再运用平行的本质特征去解释生活中的平移现象，从而对“平行”的概念有了更深刻的理解。

[教学思考]在上述教学中，教师基于学生的认知难点，通过动态处理教学，带领学生从“两条直线不相交”这一外在表征入手，充分感知平面内两条直线的空间关系，把从平移中获得的经验迁移到对平行线的认知中，从而使“平行线之间距离处处相等”这个隐藏的本质属性得以显性化，加深学生对概念本质的深度理解，突破几何概念教学的难点，发展学生的空间观念。

二、借助动态处理，拓宽概念外延

在几何概念教学中，教材一般是通过基本图形的共性特征来呈现几何概念的本质属性，这样教学往往会造成学生思维定式，对此教师应通过动态处理图形，让学生从图形的“变化”中感悟“不变”的本质，从而有效拓宽概念的外延，帮助学生完善认知结构。

例如，在“三角形的认识”的教学中，学生在学了高的概念之后，对直角三角形和钝角三角形的高依然认识模糊，存在认知难点，为此，笔者从动态处理的角度展开了三个层次的教学。

层次一，呈现动态变化，感知几何规律。

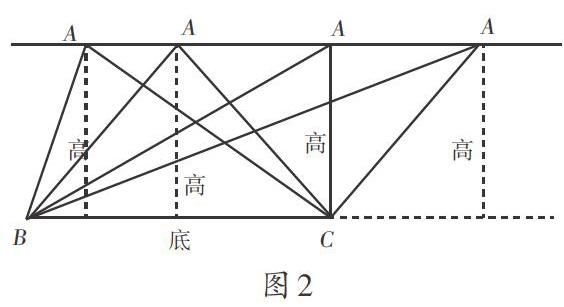
笔者动态演示图2，在两条平行线间画一个锐角三角形ABC，然后以BC为底畫出三角形的高；接着，把顶点A沿着平行线中的一条直线向右平移。

笔者引导学生观察与思考：这些三角形的形状、底边和高，哪些发生了变化，哪些没有发生变化？学生经过观察讨论后认为，三角形的形状在变化，但是底没有变化；三角形的高随着顶点在移动，但是长短没有变化。笔者继续追问：“在整个过程中，高的位置在移动变化，这个变化和三角形的形状变化之间有什么样的关联？学生观察后认为，高的位置越来越靠近AC这条边。此时，学生观察到直角边和三角形的高重合，由此准确得出结论：直角边AC既是三角形的边，同时又是三角形的高。

层次二，在变化中求关联，拓宽概念外延。

当学生认识了直角边上的高之后，笔者追问：“如果直角三角形的顶点A继续向右边平移，会得到什么样的三角形？它的高会在什么位置？”通过动态演示，学生发现钝角三角形的高在三角形的外面——从三角形的顶点A向它的对边BC所作的一条垂直线段。同时还知道了：不管三角形的哪一条高，都是顶点到它对边所作的一条垂直线段；锐角三角形的高在三角形的里面，直角三角形的高与直角边重叠，而钝角三角形的高在三角形的外面。

层次三，动态联通，突破概念学习难点。

在画高时，学生无法准确找到高所在的位置。为了突破这个难点，笔者引导学生动手画高来进行概念的动态联通。笔者先出示一个钝角三角形，让学生画出一条钝角边上的高，看看应该把三角尺放在什么位置合适。学生认为，让三角尺的一条直角边和三角形的底边重合，通过平移三角板，找到高的准确位置，直到三角尺的另一个直角紧靠三角形的顶点，这样才能画好高。

[教学思考]上述教学中，笔者先从锐角三角形入手，让学生通过动态演示观察图形的变化，感悟图形不变的本质；接着从直角三角形拓展到钝角三角形，克服了“三角形的高一定在三角形之内”的定式思维，让学生牢牢把握图形的变化本质，从中感悟三角形的“高”的不变属性；最后引导学生结合平移高的方法画出钝角三角形的高，顺利实现了原有数学经验的融通，由此拓宽了三角形这个几何概念的外延，丰富和完善了学生的认知结构。

总之，在小学数学几何教学中，教师多一些动态处理，能够将抽象的数学几何概念转化成动态的直观表象，帮助学生建立简洁清晰的空间关系，促进学生空间观念的深刻发展。

（责编 黄春香）