分布式光伏电站可靠性评价

杨 波，桑丙玉，崔红芬，袁晓冬,马 磊，孙耀杰

(1.中国电力科学研究院，南京 210003; 2.江苏省电力公司电力科学研究院，南京 210024；3.复旦大学 光源与照明工程系，上海 200433)

分布式光伏电站可靠性评价

杨 波1，桑丙玉1，崔红芬1，袁晓冬2,马 磊3，孙耀杰3

(1.中国电力科学研究院，南京 210003; 2.江苏省电力公司电力科学研究院，南京 210024；3.复旦大学 光源与照明工程系，上海 200433)

随着光伏发电大规模增长，光伏电站的可靠性评价受到了更多关注．本文通过分析分布式电站特征问题，如复杂环境、电网波动性大、散热条件差、复杂安装条件等，并运用故障树理论建立了分布式光伏电站的可靠性评价方法．通过对系统中各器件的失效模型进行分析，获得发电系统的整体失效数据，结论提出了几种合理改善电站可靠性的措施意见．该结论有助于建立更加灵活高效的分布式光伏发电系统维护策略，并为优化分布式系统提供一整套思路，为未来光伏电站配置储能系统提供评价指标参考．

可靠性评价； 分布式光伏电站； 故障树； 失效率

近年来，光伏(Photovoltaic, PV)发电的规模在世界范围内保持高速平稳增长．据美国Mercom Capital咨询公司预测，中国2016年新增光伏装机容量将达到19.5GW[1]．由于光伏电站的收益稳定、寿命长，因此可作为长线投资的重要渠道，政府光伏扶贫文件明确指出，到2020年以光伏扶贫的方式要保障200万建档贫困户的扶贫指标，其中集中式和村级分布式电站都将各自占据相当的比重[2]．

光伏电站的初始投入成本大，加之扶贫对系统运行的寿命要求高，因此提高光伏电站运行期间的稳定性，可以有效减少均化度电成本，控制运维成本，实现最短期的投资回报收益．发达国家如美国、德国，针对光伏发电系统的可靠性，特别是逆变器，进行了大量试验．以Sandia实验室[3]和Florida太阳能中心[4]为例，都开展了相应的实证项目，用于收集电站现场的可靠性数据．同样，逆变器制造商在进行产品的加速老化试验过程中，也收集了大量故障率数据．以公开发表文献的美国乔治亚理工学院自1996年起建立342kW的光伏屋顶电站为参考，其大部分是逆变器导致的故障，包括电流传感器、风扇、绝缘栅双极型晶体管(Insulated Gate Bipolar Transistor, IGBT)模块等子系统故障[5-6]．

国内外针对集中式光伏电站的研究较为全面，既包含了逆变器单体在拓扑、可靠性等方面的优化，又包含电站系统对电网的影响研究．文献[7]中主要针对并网接入标准中电站低电压穿越问题研究控制策略和测试方法，文献[8-12]对目前集中型光伏逆变器、电站和独立式光伏储能电站的可靠性不高等问题进行了分析并提出提升技术．而分布式系统的研究文献则主要集中在逆变器拓扑上，如文献[13-14]的HB-ZVR结构和H5结构，对系统整体的研究相对较少．由于分布式系统与集中式在并网接入环境、工作环境、安装条件和系统拓扑等存在显著的差异，因此集中式电站的可靠性研究无法适用于分布式．

为此，本文特别针对分布式光伏发电系统，在基于故障树理论[15-16]的基础上建立可靠性评价方法．论文首先对比了集中式和分布式光伏系统在电气结构关键节点的差异；然后结合故障树理论，从部件到整体的分析计算了分布式光伏系统的可靠性；接着，通过引用文献中光伏部件的故障率参数，对可靠性模型体系进行了验证，并针对重点影响光伏系统可靠性的关键环节进行了分析．

1 分布式与集中式光伏系统的电气拓扑差异

典型的分布式系统如图1所示，主要器件依次是光伏组件，组串型逆变器，交流配电柜，电能计量表等，一般用于居民屋顶、空地等场所，对环境参数及电气参数的收集能力较弱，容易成为可靠性分析的盲点．

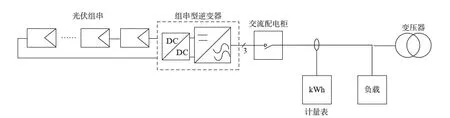
图1 分布式光伏发电系统电气拓扑结构Fig.1 Topological structure of the distributed PV system

相对集中式光伏电站，分布式系统主要在以下4个方面存在显著差异：

1) 如图1所示，集中式电站在光伏阵列和逆变器之间，一般存在一级或两级汇流箱；而分布式则由多个光伏组件串联后直接接入组串型逆变器．

2) 组串型逆变器由含独立MPPT(Maximum Power Point Tracking)功能的DC/DC变换器和DC/AC逆变器这两级结构组成，而集中型逆变器仅包含DC/AC部分，不存在直流升压部分．

3) 交流侧分布式系统无变压器，无差动电路断路器等装置，而通过逆变器中的交流继电器保护，并直接接入交流配电柜的电网接入点，再通过电能计量表输出，因此直接面对电网，受到电网波动影响较大．

4) 集中式电站一般位于开阔地区，逆变器、配电都有专门的机房，受环境影响相对较小；分布式系统所用的组串型逆变器防护等级可支持安装于室外，一般可安装于屋顶、山地、水面、大棚等位置，其工作环境相对复杂．

综上所述，相对集中式电站，分布式系统所用的部件相对较少，但接入电网条件、工作环境及安装方式更为复杂，亟待进行可靠性评价的研究．

2 可靠性评价

2.1 系统故障树模型

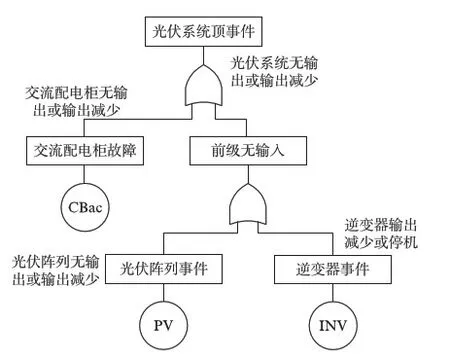
图2 分布式光伏发电系统故障树Fig.2 Fault tree of the distributed PV system

由于光伏电站工作在荒山、湖面等荒野地区的几率较大，暴露在极端条件和周期性的湿热、电应力下，逆变器可靠性的准确评估需要大量相同或相似系统的数据或系统长时间观测下的数据来支持．目前主要有两种途径： 一种是通过大规模逆变器群在实际电站或加速老化试验的数据获得，代表性的是Sandia和Florida实验室；另一种是通过现有可靠性预测标准对部件的故障率预测，并通过故障模型汇总获得子系统的故障率，最终形成整体故障率，代表是最早出现并一直广泛应用的MIL-HDBK-217F标准，该标准能够提供电子仪器的可靠性预测．

实际场测试的定量数据仅针对某个特定环境和特定逆变器，无法应用到其他逆变器设计中．本文采用故障树理论，对分布式发电系统的故障预测进行快速有效的分析： 故障树理论能够从分析部件之间的关系开始，逐次联接，形成整体的系统性关联．特别适合设备较少、主要通过串联方式连接的分布式系统(包括光伏组件)．本文将分布式光伏系统的电气结构图转换为如图2所示的故障树分析图．

圆形图标： 表示底事件，是引发系统故障的基本项，发生不需要前端输入；或门： 表示当或门下面至少有一个事件发生时，或门上方的事件才会发生；方形图标： 故障树的主要模块表示中间事件，可以由其他的中间事件和底事件组合形成．

其中： PV表示光伏组件；INV表示逆变器；CBac表示交流配电柜(主要包含交流断路器)；其中，TOP EVENT=PV+INV+CBac．

光伏发电系统各个器件的失效概率，统计表格如表1所示，但文献[5]中对应的失效率为集中型逆变器的，因此本文接下来重新验证组串型逆变器的可靠性．相对于组件、交流电路断路器等简单系统，组串型逆变器的结构和工作机理复杂，从外部因素考虑，与它的光照能量密度、环境温度和输入功率等级密切相关；从内部因素考虑，与其所采用的IGBT、直流母线电容、电感、散热装置等有着显著关联，因此失效机理较为复杂，要考虑多种情况的相关性．

组串型逆变器包含6个主要子系统： 母线电容，升压部分，逆变部分，交流继电器，显示屏及机内通讯.本文从这6个子系统角度出发建立故障率，并根据这6个子系统，验证表1中逆变器的失效率．

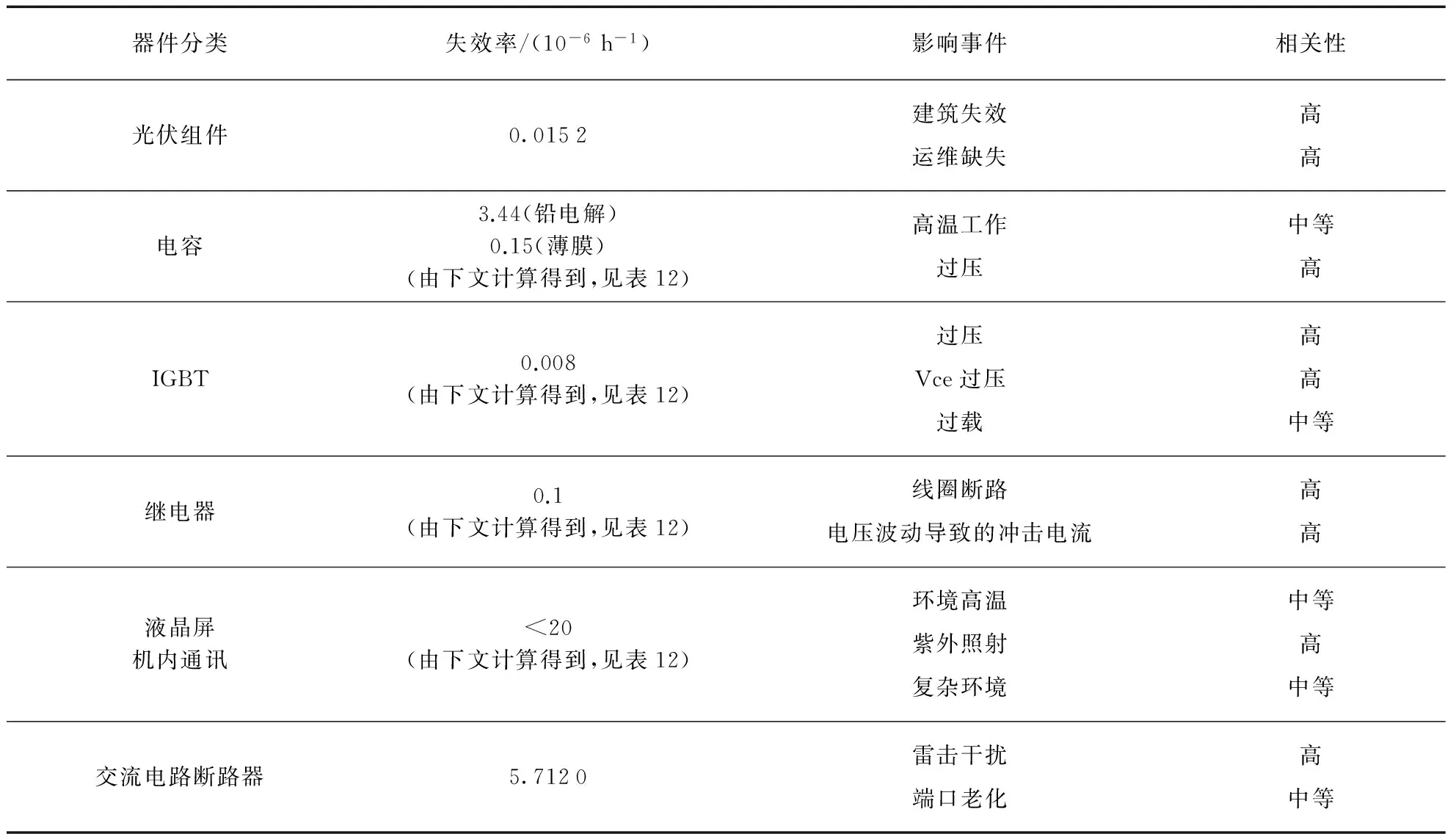
表1 分布式光伏电系统元件失效率Tab.1 Failure rates of the components in the distributed PV system

*对逆变器来说，液晶屏如果产生故障，大部分情况仍可发电，但会带来运维上的认知困难，因此也作为一种逆变器失效.

2.2 失效模型理论

首先，子系统故障概率应按照器件的指数分布，它的可靠性概率和平均故障时间如下所示：

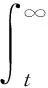
(1)

(2)

R(t)=e-λt,

(3)

式(1)中，f(t)为部件的故障概率密度函数，R(t)为系统自时刻t起的可靠性概率；式(2)中失效率λ为系统平均故障时间的倒数；式(3)为可靠性函数．

需要说明的是，本文为简化计算起见，使用指数分布函数作为可靠性函数，其他如幂指数分布函数、Weibull分布函数也可适用．由于本文旨在提供一种用于可靠性模型建立和评价的方法，更注重定性的结果，在方法明确后，只要通过数据得到各个组件的真实失效概率分布函数，就可以代入到该模型中，得到精确的评估结果．实际上，光伏发电系统中器件实际的故障概率密度函数，都需要在特征环境下进行长时间或相对昂贵的加速寿命测试才能得到，得到的数据如果用Weibull分布函数等拟合可能更准确．但如果获取的数据量不足，会导致了Weibull函数进行故障预测时不确定度增加，影响最终的精度．

2.3 逆变器失效模型验证计算

1) 母线电容

针对直流母线，如采用铝电解电容，其故障率模型为：

λC=λb·πCV·πQ·πE，

(4)

其中：λC为电容的工作失效率；λb为电容的基本失效率；πCV为容值因子；πQ为品质因子；πE为环境因子．电容在125℃额定工作温度下的基本故障率λb计算公式为：

(5)

πCV=0.34C0.18,

(6)

其中：S为使用电压与额定电压的比值；T为工作环境温度，以℃为单位．

从失效率模型发现，当使用电压增大或使用温度升高，基本失效率变大，导致工作失效率λC变大．

以10kW逆变器为例，逆变器采用1100μF/450V电容，额定工作在375V，工作温度85℃，电容两两串联，3组并联，共6个．根据容值计算πCV，取1.20；电解电容一般为非军标，πQ取10；分布式逆变器一般处于室内，πE取1.0；λb计算值为0.2864；因此可以得到参数λC=3.44，即每个电容的工作失效率为3.44×10-6h-1．

如采用薄膜电容，需要评估薄膜电容的失效率．薄膜电容包括聚碳酸酷、聚乙烯聚醋、纸、塑料和金属化塑料(PC和PET)、金属化聚碳酸醋、金属化纸和聚乙烯聚醋等，在MIL-HDBK-217F标准中，大部分薄膜电池的指数系数接近而乘积系数稍有不同，本文选择最差的一种故障模型，如下：

(7)

πCV=1.2C0.092,

(8)

其中，薄膜电容为55μF/500V，工作温度为85℃，额定工作在375V，电容两两串联，10组并联，共20个．计算πCV得1.73；πQ一般为非军标，取3；πE仍取1.0；λb计算值为0.29；因此可以得到参数λC=0.15×10-6h-1.

2) 升压部分及逆变部分

升压部分及逆变器部分至少包含4个桥臂(比集中式要多至少1个桥臂)；单个桥臂包含2个IGBT．因此需要建立IGBT的故障模型．

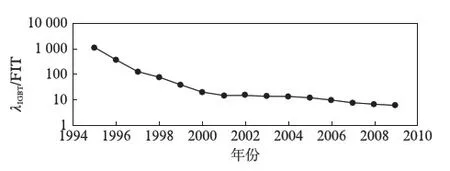
图3 IGBT的FIT参数Fig.3 FIT of IGBT

当今由于高质量的生产过程和很低的缺陷密度，导致要测量IGBT的失效率需要巨大的元件数量．在较早时期便进行修订的相关标准中没有建立IGBT的故障率，因此IGBT的故障率参数主要通过厂商提供的数据进行．如图3所示，根据国际主流功率器件厂商英飞凌的相关故障率(Failures In Time, FIT)数据可知，IGBT的故障率可近似为λIGBT=0.008×10-6h-1(1 FIT代表1×10-9h-1)．

3) 交流继电器

λrelay=λr·πES·πS·πT,

(9)

其中λr为参考条件下得到的失效率，其公式为：

(10)

其中：m为形状参数；η为特征寿命；γ为位置参数．

πES为电强度系数；πS为工作频率系数；πT为温度系数．这里，在存在电压波动的情况下，选择合适型号，继电器一般能保证故障率λrelay=0.1(单位为10-6h-1).

4) 液晶屏

液晶屏的寿命取决于背光、偏振膜等材料．背光灯的理论平均寿命为5×104～6×104h．偏振膜容易被氧气、光线尤其是紫外线损坏，在长时间被紫外照射后效果就会不好，因而出现故障的失效率较大．

5) 机内通讯

由于工作环境存在空气污染，或组串型逆变器长时间工作于室外，通风系统会给机内带来少量灰尘，污染机内通讯设备的概率较大．由于通讯设备的电流信号频率非常快，会导致电路存在微弱磁场，更加吸引灰尘的吸附和累积，严重影响接头接触，并造成静电积累，产生错误的信号．按照对通讯模块的民用要求，平均失效间隔时间(Mean Time Between Failure, MTBF)≤5×104h，因此故障率要低于20×10-6h-1．

6) 子系统组成的逆变器可靠性

根据以上计算，以及逆变器所用器件的清单，可得到一般逆变器的故障率：

∑λ=nCλC+nIGBTλIGBT+nrelayλrelay+λLC+λCOM

(11)

通过计算，得到某两电平组串型逆变器的故障率见表2.

表2 逆变器子系统故障率及总故障率表Tab.2 Failure rates of the sub-system and total failure rates

注： 采用电解电容、不进行维护时的总故障率为61.304；采用薄膜电容、进行维护时的总故障率为3.664.

当考虑20年的时间周期时(即t=20×365×24h)，将组件、逆变器、交流电路断路器等代入指数分布函数式：

(12)

其中：i为组件、逆变器、交流电路断路器等系统编号(见表1)；mi代表各系统所用单个元器件的数量；λi为各系统单个元器件的故障率；ti为子系统更换时间(这里ti一致，为20年)

10kW逆变器中，以每个组件285W为参考，需要38块组件，与逆变器功率配比为1.08∶1．

采用电解电容情况下，逆变器可靠性为(从前往后分别为逆变器、组件、交流电路断路器的故障率)：

Rtot=exp[-(61.30+0.0152×38+5.712)×10-6×20×365×24]=7.1981×10-6.

(13)

采用薄膜电容情况下，逆变器可靠性为：

Rtot=exp[-(3.66+0.0152×38+5.712)×10-6×20×365×24]=0.175.

(14)

3 讨 论

1) 母线电容选择

从上述计算可以看出： 随着分布式逆变器选用母线电容的不同，可靠性呈现不同等级；另一方面，当逆变器选用薄膜电容后，可靠性衰减不是最为明显的一个，而变为交流电路断路器．

根据美国电力研究院(Electric Power Research Institute, EPRI)曾对薄膜电容等效老化寿命为50年的加速寿命试验，薄膜电容在逆变器寿命周期内不需要考虑其老化问题．

2) 运行时间

从式(12)可以看出： 随着运行时间的增长，光伏电站各个器件的可靠性指标会迅速下降．比如，1年后分布式光伏发电系统的可靠性有91.65%，而20年后正常工作的可靠性是17.50%．这意味着如果不进行定期运维，分布式光伏系统经过长时间运行后，将无法正常工作．

同时，从表2还可以看出，当无法对组件进行定期维护时，鸟粪、灰尘等一方面会严重影响组件的发电性能，另一方面会逐渐降低组件的可靠性，最终导致失效．

3) 环境因素

由于受到恶劣环境影响，导致出现建筑物失效(如台风造成支架掀翻、盐雾导致支架腐蚀变形等情况)或逆变器失效(高温带来的老化、高湿带来的短路等情况)．因此，在电站设计初期，就要认真考察建筑，针对环境做好支架设计和遮蔽设施，以及合适逆变器的选择，如在污染严重地区采用无风机自然散热类型可以有效减少机内通讯失效概率．

4) 目前新方案带来的影响

当前出现了320W/72片电池片组成的新型组件，同时，部分逆变器系统输入电压可达1500V，通过上述可以看出这些新方案的影响： 在采用320W的新型组件后，由于器件数量减少，分布式光伏发电系统可靠性会增加，但总体影响微弱．如系统使用1500V新型逆变器时，需充分考虑工作电压对电容可靠性的影响，防止电容的快速老化．

4 总 结

针对当前光伏发电规模增加迅速的现状，以及当前对分布式光伏发电系统可靠性评价研究的不足，本文针对分布式发电系统在复杂环境、电网波动性较大、建筑安装易失效等情况，提出一种基于故障树理论的可靠性评价方法．文章通过结合系统的故障模型，明确了选择薄膜电容、组件运维、初期建筑及支架考察、自然散热及紫外线遮蔽等措施对可靠性的提升作用，为分布式电站优化提供了有效思路，为未来光伏电站配置储能系统提供评价指标参考．

[1] 电缆网.2016年全球太阳能新增容量约64.7GW中国继续领跑 [R].2016.

[2] 国家发展和改革委员会办公厅.关于实施光伏发电扶贫工作的意见[Z].2016.

[3] MOORE L. Sandia’s PV reliability database： Helping business do business [J]. 2001.

[4] DHERE N G. Reliability of PV modules and balance-of-system components [C]∥the 31st IEEE Photovoltaic Specialists Conference, Orlando, Florida, USA, IEEE Press, 2005,1570-1576.

[7] 罗劲松.大型光伏电站低电压穿越技术研究 [D].西宁： 宁夏大学.2014.

[8] RISTOW A, BEGOVIC M, PREGELJ A,etal. Development of a methodology for improving photovoltaic inverter reliability [J].IEEETransactionsonIndustrialElectronics, 2008,55(7)： 2581-2592.

[9] LOCKHEED M. Reliability prediction of electronic equipment [M]. Washington DC, USA： HIS Press, 1991.

[10] OOZEKI T, YAMADA T, KATO K,etal. An analysis of reliability for photovoltaic systems on the field test project for photovoltaic in Japan [C]∥Solar World Congress of the International-Solar-Energy-Society. Beijing, China： Springer Press, 2007： 1628-1632.

[11] KABAMBALIKA L. Simulation and performance evaluation of battery based stand-alone photovoltaic systems of Malawi [D].Taoyuan, Taiwan, China： National Central University, 2009.

[12] 胡文杰，孙耀杰，林燕丹，等.集中式光伏电站的可靠性评价 [J].复旦学报(自然科学版).2015,54(5)： 579-585.

[13] KEREKES T, TEODORESCU R, RODRIGUEZ P,etal. A new high-efficiency single-phase transformerless PV inverter topology [J].IEEETransactionsonIndustrialElectronics, 2011,58(1)： 184-191.

[14] 肖华锋.光伏发电高效利用的关键技术研究 [M].南京： 南京航空航天大学,2010.

[15] ZINI G, MANGEANT C, MERTEN J. Reliability of large-scale grid-connected photovoltaic systems [J].RenewableEnergy, 2011,36(9)： 2334-2340.

[16] AHADI A, GHADIMI N, MIRABBASI D. Reliability assessment for components of large scale photovoltaic systems [J].JournalofPowerSources, 2014,264： 211-219.

ReliabilityAssessmentoftheDistributedPVStation

YANGBo1,SANGBingyu1,CUIHongfen1,YUANXiaodong2,MALei3,SUNYaojie3

(1.ChinaElectricPowerResearchInstitute,Nanjing210003,China;2.JiangsuElectricPowerCompanyResearchInstitute,Nanjing210024,China；3.DepartmentofLightSourceandEngineering,FudanUniversity,Shanghai200433,China)

With large-scale growth of the PV station, the PV station reliability assessment has

more attention. This paper has established the reliability assessment method for the distributed PV station by using fault tree theory and analyzing the characteristics of the distributed PV station, such as complex environment, power fluctuation, poor cooling conditions and complex installation conditions. By analyzing the failure model of the devices in the PV system, the whole failure data of the PV station is obtained. In conclusion, some measures to improve the reliability of the PV station has been put forward. These conclusions are helpful to establish a more flexible and efficient distributed PV station maintenance strategy, and provide a set of ideas for the optimization of the distributed PV system.

reliability assessment; distributed Photovoltaic station; fault tree; failure rates

0427-7104(2017)06-0732-07

2016-11-12

杨 波(1977—)，男，高级工程师；孙耀杰，男，教授，通信联系人，E-mail： yjsun@fudan.edu.cn.

TP271

A