分数阶扩散方程中多参数联合数值反演
2018-01-10池光胜李功胜
池光胜,李功胜,2
(1.内蒙古工业大学 理学院,呼和浩特 010051; 2.山东理工大学 理学院,淄博 255049)
分数阶扩散方程中多参数联合数值反演
池光胜1,李功胜1,2
(1.内蒙古工业大学 理学院,呼和浩特 010051; 2.山东理工大学 理学院,淄博 255049)
考虑一维空间分数阶扩散方程中同时确定空间微分阶数、扩散系数和源项的多参数联合反演问题.基于空间分数阶导数离散系数的性质和快速傅里叶变换,给出求解正问题的一种新的差分格式.利用同伦正则化方法对所提的空间微分阶数、扩散系数和源项的多参数联合反演问题进行精确数据与扰动数据情形下的数值反演.结果表明: 同伦正则化算法对空间分数阶扩散中的多参数联合反演是有效的.
分数阶扩散方程; 差分格式; 多参数联合反问题; 数值反演
1 研究背景
作为整数阶的推广,分数阶具有非局部性,可以更好地描述生活中整数阶无法刻划的复杂系统.近年来,分数阶扩散方程应用于地下水污染迁移、生物学、物理学,甚至在金融学中都起到越来越重要的作用.有关研究表明: 在地下水污染迁移中,分数阶扩散方程在描述多孔介质中具有非费克现象的溶质运移过程时,能够更好地模拟溶质提前穿透或严重拖尾等非线性迁移行为.若考虑非局域性和空间相关性,则得到空间分数阶扩散方程.另一方面,一旦建立了一个分数阶扩散的初步模型,求解和分析模型中难以直接测量的参数就成为一个很重要的问题.这就导致了对于分数阶扩散方程及其参数反演问题的研究.可以说,分数阶扩散相关反问题研究对于认识污染物在多孔介质中的反常扩散行为具有重要的科学意义和应用前景.
近20年以来国内外学者对于空间分数阶扩散方程正问题的求解做了大量的研究.对解析解的研究常用的方法有分离变量法[1]、傅里叶变换和拉普拉斯变换法[2-3].数值方法包括有限差分方法[4-5]、有限元方法[6]和谱方法[7]等.对于给定的分数阶扩散方程,运用一般数值方法得到的系数矩阵是稠密的,用高斯消去法计算量为O(N3),存储量为O(N2).为了节约计算时间,王宏等[8]提出一种计算空间分数阶扩散方程的快速算法,在保证计算精度的同时,缩短了计算时间.考虑到反问题的计算时间与正问题计算时间的相关性,本文在文献[8]的基础上,对分数阶扩散方程正问题进行数值求解.
对于分数阶扩散中的反问题的研究,大多是针对时间分数阶扩散方程中反问题的[9-12],由于空间分数阶模型正问题研究的困难性,相应的反问题研究较少,如韦徽[13]等利用最佳摄动量算法的思想对一维空间分数阶扩散方程中的源项系数进行了反演研究.郑光辉与魏婷[14]提出了求解分数阶扩散方程反问题的两种正则化方法.池光胜[15]同样应用最佳摄动量算法探讨了一维空间分数阶对流弥散方程中依赖空间变量的源项反问题,对于不同形式的源项函数进行了有效的数值模拟.贾现正[16]利用同伦正则化算法对时间空间分数阶对流扩散方程中的微分阶数进行了数值反演.邓伟华[17]利用正则化算法对空间分数阶扩散方程的源项进行了反问题的研究.
由于微分阶数是刻划分数阶扩散的首要指标,扩散系数描绘空间非均质性,源项反映外界力属性,在实际问题中这些量往往都是是未知的,也是难以通过实验手段来测量的,因此,本文考虑微分阶数、扩散系数和源项同时反演.由于其高病态性,使用最佳摄动量算法无法实现问题的求解.考虑到同伦方法在求解线性代数方程中的广泛应用,将最佳摄动量算法和同伦方法结合形成新的迭代算法,可以扩大收敛区域,且成功运用于扩散方程相关反问题的研究中[16],本文继续运用这种同伦正则化算法.
2 正问题及其数值求解
对于l>0,T>0,考虑一维(左侧)空间分数阶扩散方程
(1)
式中:c(x,t)为状态变量; 1<α<2为空间微分阶数;D(x)>0为扩散系数;f(x,t)为源/汇项.当α=2时,方程(1)即为经典的整数阶扩散方程.方程(1)中的空间分数阶导数用Riemann-Liouville的定义[3]:
对于方程(1),给定初始条件为
c(x,0)=g(x) 0≤x≤l,
(2)
边值条件为
c(0,t)=c(l,t)=0 0 (3) 对该类型正问题的数值求解,本文在文献[8]的基础上,构造有效的差分格式. 首先给出正问题求解的一般的隐式差分格式.设xi=ih,h>0,i=0, 1,…,M;tn=nτ,τ>0,n=0, 1,…,N,其中h和τ分别是空间和时间步长. Riemann-Liouville分数阶导数采用移位的Grünwald公式离散为 (4) (I+An+1)Cn+1=Cn+τfn+1; (5) (6) 注1文献[4]给出了差分格式(5)的无条件稳定性与收敛性的证明. 式(5)即为一般的隐式差分格式.由于差分格式(5)的系数矩阵为满秩,因此运算量为O(M3),每个时间步长需要O(M2)的存储量.下面给出快速求解的差分格式. (7) (8) 根据上述讨论,我们将An+1作如下分解: (9) 即 对Cn+1作近似分解,则 (10) 将式(10)代入式(5)可得新的差分格式为 (11) 由以上的分析可得,格式(11)将式(5)的系数矩阵计算存储量由O(M3)降为O(Mlog22M), 但是格式(11)右侧的运算量和存储需求均为O(M2).下面将给出差分格式(11)右侧的快速算法. 引理2[19]若Bn=Bn(i,j)=b(j-i),i,j=1,2,…,n是一个循环矩阵,则 其中:b=(b0,bn-1,…,b2,b1)T是矩阵Bn的第一列;Fn是n×n阶傅里叶变换矩阵. 1)IMERG日平均降水量的空间分布连续性较好,能够较好地反映我国降水量的分布特点,但局部地区较CGDPA偏低。IMERG与CGDPA日平均降水量的相关系数为0.91,均方根误差为0.66 mm/d,相对偏差为5.32%。IMERG与CGDPA在东部地区的相关系数为0.94,而西部地区为0.72。两者在东部地区的均方根误差为0.52 mm/d,西部地区为0.81 mm/d;东部地区的相对误差为-1.62%,西部为-18.6%。IMERG在东部地区的降水估计精度明显优于西部。 步骤2令w2M-2,L=F2M-2C2M-2,F2M-2C2M-2是C2M-2的傅里叶变换; 步骤3令v2M-2,L=F2M-2b2M-2,L,b2M-2,L是B2M-2,L的第一列; 通过以上分析可知,利用快速算法可将格式(11)右侧运算量由O(M2)降为O(Mlog2M),存储需求由O(M2)降为O(M). 下面就以一个分数阶扩散方程为例,说明如何利用差分格式(11)进行数值计算. 先看离散点数对数值计算的影响.不妨取空间微分阶数α=1.9,应用差分格式(11)计算获得数值解,表1给出了t=1时空间、时间离散点数与解的相对误差,其中M,N分别表示空间、时间离散点数. 由表1可以看出,随着空间、时间离散点数的增加,解误差逐步变小.下面取定M=N=27,考察微分阶数变化对数值解的影响,计算结果列于表2. 表1 t=1时空间、时间离散点数对误差的影响Tab.1 The influence of the time and space discrete points on the error at t=1 表2 t=1时空间微分阶数对误差的影响Tab.2 The influence of the space differential order on the error at t=1 从表2可以看出,空间微分阶数对误差基本没有影响.下面考察快速算法(Fast Finite Difference, FFD)和一般的有限差分方法(Finite Difference, FD)对数值解的影响,其中TCPU(单位: s)表示计算时间,计算结果列于表3. 表3 t=1时FFD与FD对数值解的影响Tab.3 The influence of FFD and FD on numerical solution at t=1 图1 α=1.9时的精确解与数值解(t=1)Fig.1 The comparison between exact solution and numerical solution at α=1.9 and t=1 从表3看出,新的差分格式利用快速算法比一般的有限差分方法除了计算精度略高以外还缩短了计算时间.图1绘制了α=1.9,在t=1时刻的精确解与数值解(M=N=27). 对于分数阶扩散初边值问题泛定方程(1),当扩散系数D(x)为常数D,源项具有形式f(x,t)=a(x)λ(t)时,给定附加数据为 c(x,T)=θ(x) 0≤x≤l. (12) 当α,D,a(x)给定时,称(1)为正问题,可以通过上节中的差分方法求解;若α,D,a(x)未知,则初边值问题(1)~(3)与附加数据(12)就构成了参数识别的反演问题.本节就考虑同时确定微分阶数α,扩散系数D和源项系数a(x)的多参数反演问题.虽然反问题解的唯一性、稳定性等理论分析很重要,不过本文将关注反演算法及数值反演. Qn+1=Qn+δQn. (13) 所以Q的确定问题可以转化为δQn的确定问题,并且δQn可以由下列目标函数的局部极小值来确定: 这里同伦参数λ参考人工神经网络的传递函数,即 (14) 其中:N0为初值选取参数;β为下降速率参数;λ(N)为第N个迭代步时正则参数的取值.这里有两个可调参数,β和N0.其中β用于调整正则化参数的下降速率,一般该参数取0.5左右的数值.参数N0一般可选为0~5之间的整数,主要保证计算初期的迭代稳定进行.因为δQn是一个微小的扰动量,把c(x,T;Qn+δQn)利用多元泰勒公式展开得到 于是有 进一步将区域[0,l]离散为0 求解minF(δQn)相当于求解规范方程 ((1-λ(N))HTH+λ(N)I)δQn=(1-λ(N))HT(V-U), (15) 其中: H=(hms)M×Nm=1,2,…,M,s=1,2,…,N; U=(c(x1,T;Qn),c(x2,T;Qn),…,c(xM,T;Qn))T; V=(θ(x1),θ(x2),…,θ(xM))T; 其中:z是数值微分步长;I是单位矩阵.这样,适当选择同伦参数λ(N),可从式(15)中解得对应于xm的摄动量δQn,进而再通过迭代过程(13)可逐步求得原来反问题的解. 在给定真解QR=(αR,DR,a(x)R)的情况下,反演算法实施步骤为: 步骤1给定数值微分步长z及迭代控制收敛精度eps,由真解代入正问题的差分格式进行计算,得到附加数据向量V; 步骤2给定初始迭代Qn(n=0,1,…),求得U与矩阵H; 步骤3按式(15)计算最佳摄动量δQn,其中同伦参数按式(14)选取; 步骤4判断是否满足‖δQn‖≤eps,若成立,则Qn+1=Qn+δQn即为所求的反演解,算法终止;否则由Qn+1代替Qn,再转到步骤2继续进行. 本节对于微分阶数、扩散系数和源项多参数联合反问题进行数值反演.如前所述,每个算例中给定真解,并利用其得到终值时刻的附加数据,然后应用同伦正则化算法进行反演重建.以下若无特别说明,正问题计算中取区域长度l=1,终值时刻T=1,扩散系数D=1,且取零边界条件,初始函数g(x)=x2(1-x),离散点数M=N=16且λ(t)=e-t;反演算法中取数值微分步长z=0.01,控制迭代收敛精度eps=10-6,同伦参数(14)中取j0=5,β=0.3. 本小节先考虑精确数据下的情形,取方程中的微分阶数α=1.9,源项系数a(x)=1-x,基向量{φi(x)=xi-1,i=1,2,3,4,则真解为QR=(1.9,1,1,-1,0,0),记Q*为数值反演解,则解的误差表示为err=‖Q*-QR‖/‖QR‖,j是迭代次数. 考察不同的数值微分步长对算法的影响,取初始迭代Q0=(1.1,0,0,0,0,0),其余参数值不变,计算结果见表4. 表4 α=1.9时,数值微分步长对反演算法的影响Tab.4 The influence of numerical differential step on inversion algorithm with α=1.9 由表4可以看出,数值微分步长对反演结果有一定的影响,不宜取的过小.再取定z=0.05,考察空间微分阶数变化对反演算法的影响,计算结果列于表5,其中α表示空间微分阶数,Q*,err及j表示意义与表4中相同. 表5 空间微分阶数对反演算法的影响Tab.5 The influence of space differential order on inversion algorithm 由表5可以看出,空间分数阶数对反演结果基本没有影响.考察下降速率参数对反演结果的影响,取α=1.9,z=0.05,其余参数不变,计算结果见表6. 表6 下降速率参数对反演算法的影响Tab.6 The influence of descent rate parameters on inversion algorithm 由表6可以看出,下降速率参数对反演结果有一定的影响,不宜取得过大,当β≥0.58时,无法计算.考察源项形式对反演结果的影响,取α=1.9,z=0.1,β=0.5,其余参数不变,计算结果见表7. 表7 源项形式对反演算法的影响Tab.7 The influence of source term on inversion algorithm 由表7可以看出,源项形式对反演结果基本没有影响.考察离散节点对反演结果的影响,取α=1.9,z=0.1,β=0.5,a(x)=1-x,其余参数不变,计算结果见表8,TCPU(单位: s)表示一次反演计算所用的CPU时间. 表8 离散节点数对反演算法的影响Tab.8 The influence of discrete point number on inversion algorithm 由表8可以看出,离散节点数的增加对反演解精度影响不大,但是对反演计算量影响较大.随着网格的加密,迭代次数稍微减少,但每次反演计算耗用的时间明显增加.当离散节点超过27时,计算失败.由此可见,离散节点不宜选取过多. 实际问题中,附加数据往往带有某种误差,对于扰动数据实施反演算法是反问题数值方法研究的重要方面.带有扰动数据的附加数据表示为 θε(x)=θ(x)(1+ξε), (28) 从表9可以看出,随着数据扰动水平的减小,反演解与精确解误差逐渐变小,表明了反演算法的稳定性.在ε=0.1%的水平下,考察快速算法(FFD)和有限差分方法(FD)对数值反演的影响,其中TCPU(单位: s)表示反演计算所用的时间,计算结果见表10. 表9 不同扰动水平下的反演结果Tab.9 The inversion results with different noisy levels 表10 给定扰动水平下FFD与FD对反演结果的影响Tab.10 The influence of FFD and FD on the inversion results with a constant noisy level 从表10可以看出,利用新的差分格式对反演解的误差并没有太大的影响,但是可以有效地节约计算时间. 本文探讨了(左侧)空间分数阶扩散方程正问题求解的差分格式,应用分数阶导数离散系数和Toeplitz矩阵的性质及快速傅里叶变换完成了由有限差分方法到快速求解的过渡.进一步,对于空间微分阶数、扩散系数和源项的多参数联合反演问题,应用一种同伦正则化算法给出了精确数据与扰动数据情形下的数值反演.结果表明: 在恰当的选取数值微分步长和下降速率参数的情况下,同伦正则化算法可以有效地处理对于空间分数阶反常扩散中的多参数联合反演问题.而高维的情形和多参数联合反演的存在唯一性分析,由于问题的高病态性,将是我们今后的主要工作. [1] 池光胜.分数微分对流弥散方程反问题的研究 [D].淄博: 山东理工大学, 2010. [2] MILL J V. Theory and applications of fractional differential equations [M]. New York,USA: Elsevier Science Ltd, 2006. [3] PODLUBNY I. Fractional differential equations[M]. New York, USA: Academic Press, 1999. [4] MEERSCHAERT M M, TADJERAN C. Finite difference approximations for fractional advection-dispersion flow equations [J].JournalofComputationalandAppliedMathematics, 2004,172(1): 65-77. [5] MEERSCHAERT M M, TADJERAN C. Finite difference approximations for two-dimensional fractional dispersion equation [J].JournalofComputationalPhysics, 2006,211(1): 249-261. [6] DENG W. Finite element method for the space and time fractional Fokker-Planck equation [J].SIAMJournalonNumericalAnalysis, 2008,47(1): 204-226. [7] LI X, XU C. Existence and uniqueness of the weak solution of the space-time fractional diffusion equation and a spectral method approximation [J].CommunicationsinComputionalPhysics, 2010,8(5): 1016-1051. [8] WANG H, WANG K, SIRCAR T. AdirectO(Nlog22N) finite difference method for fractional diffusion equations [J].JournalofComputationalPhysics, 2010,229(21): 8095-8104. [9] CHENG J, NAKAGAWA J, YAMAMOTO M,etal. Uniqueness in an inverse problem for a one-dimensional fractional diffusion equation [J].InverseProblems, 2009,25(11): 115002. [10] LI G S, GU W J, JIA X Z. Numerical inversions for space-dependent diffusion coefficient in the time fractional diffusion equation [J].JournalofInverseandIll-PosedProblems, 2012,20(3): 339-366. [11] LI G S, ZHANG D L, JIA X Z,etal. Simultaneous inversion for the space-dependent diffusion coefficient and the fractional order in the time-factional diffusion equation [J].Inverseproblems, 2013,29(6): 065014. [12] XU X, CHENG J, YAMAMOTO M. Carleman estimate for a fractional diffusion equation with half order and application [J].ApplicableAnalysis, 2011,90(9): 1355-1371. [13] WEI H, CHEN W. A coupled method for inverse source problem of spatial fractional anomalous diffusion equations [J].InverseProbleminScienceandEngineering, 2010,18(7): 945-956. [14] ZHENG G H, WEI T. Two regularization methods for solving a Riesz-Feller space-fractional backward diffusion equation [J].Inverseproblem, 2010,26(11): 115071. [15] CHI G S, LI G S, JIA X Z. Numerical inversions of a source term in the FADE with Dirichlet boundary condition using final ovservations [J].ComputersandMathematicswithapplications, 2011,62(4): 1619-1626. [16] 贾现正,张大利,李功胜,等. 空间-时间变系数对流扩散方程微分阶数的数值反演 [J]. 计算数学, 2014,36(2): 113-132. [17] TIAN W Y, LI C, DENG W H,etal. Regularization methods for unknown source in space fractional diffusion equation [J].MathematicsandComputersinsimulation, 2012,85(3): 45-56. [18] CHEN Z Q, MEERSCHAERT M M, NANE E,etal. Space-time fractional diffusion on bounded domains [J].JournalofMathematicalAnalysisandApplications, 2012,393(2): 479-488. [19] GRAY R M. Toeplitz and circulant matrices: A review [J].FoundationsandTrendsinCommunicationsandInformationTheory, 2006,2(3): 155-239. NumericalInversionsofJointParametersinFractionalDiffusionEquation CHIGuangsheng1,LIGongsheng1,2 (1.CollegeofScience,InnerMongoliaUniversityofTechnology,Hohhot010051,China;2.SchoolofScience,ShandongUniversityofTechnology,Zibo255049,China) A joint parameters inversion problem of determining the space fractional diffusion order, diffusion coefficient and source term simultaneously in 1-dimentional space fractional diffusion equation is studied. Using the property of the discrete coefficient of fractional derivative and the fast Fourier transformation, a new finite difference scheme for solving the forward problem is given. Numerical inversions with accurate data and noisy data for the joint parameters inversion problem using homotopy regularization algorithm is discussed. The numerical results show that the homotopy regularization algorithm is efficient for the joint parameters inversion in the space fractional diffusion. fractional diffusion equation; finite difference scheme; joint parameters inversion; numerical inversion 0427-7104(2017)05-0767-09 2016-03-28 国家自然科学基金(11371231) 池光胜(1985—),男,博士研究生, E-mail: chiguangsheng007@163.com. O242.1 A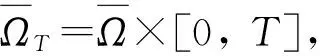
2.1 隐式差分格式





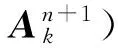
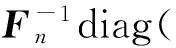
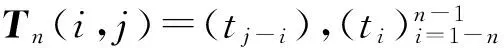
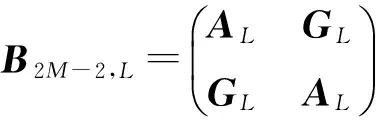
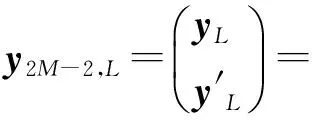
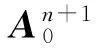
2.2 数值试验
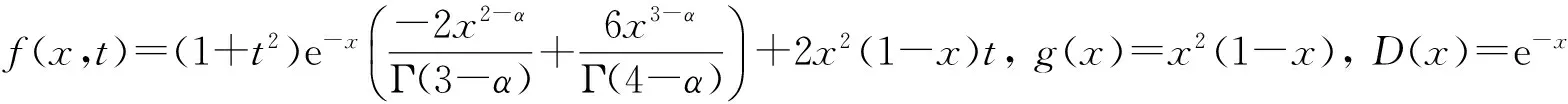
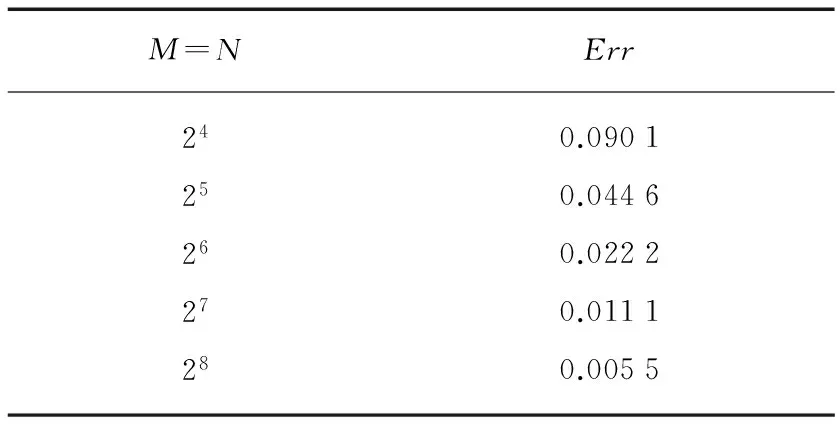
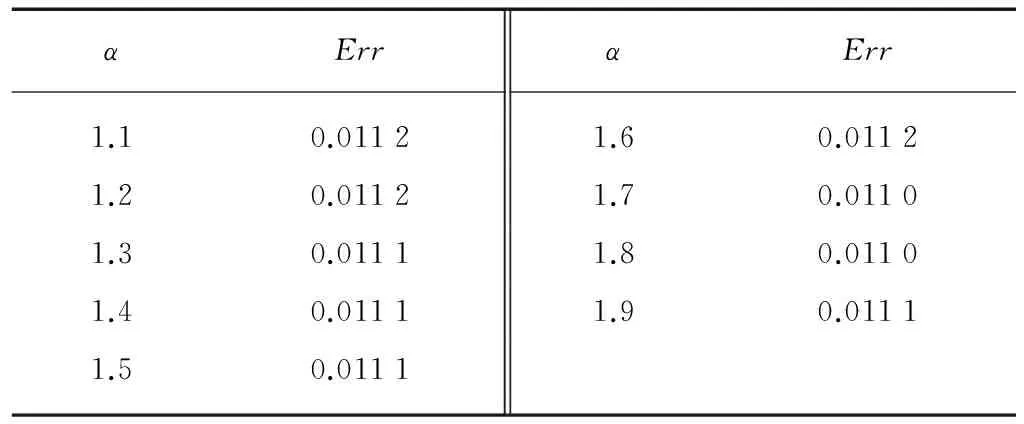
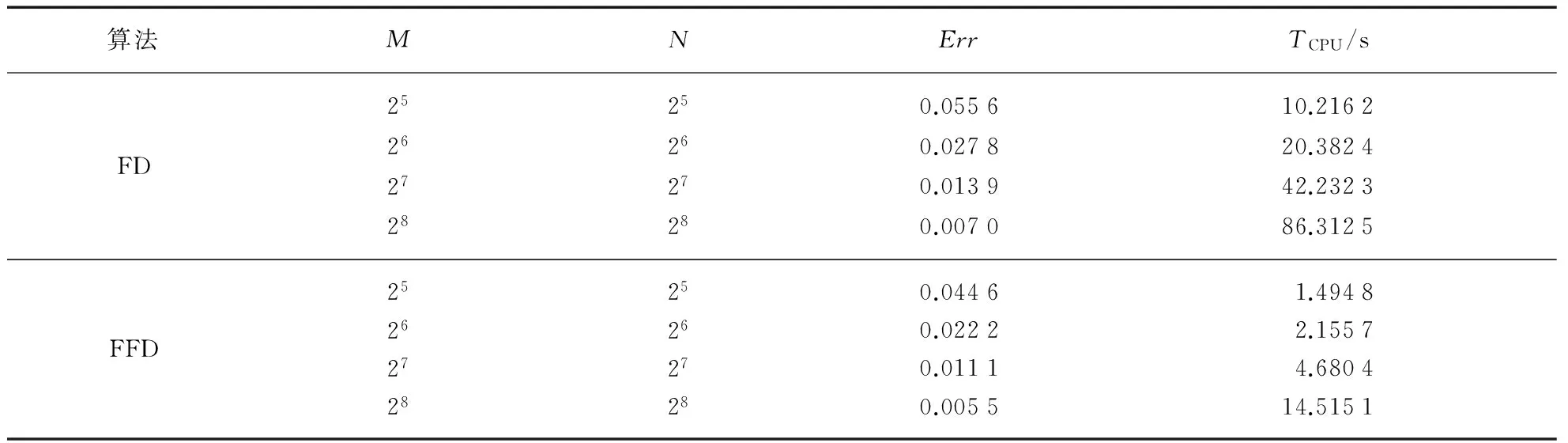
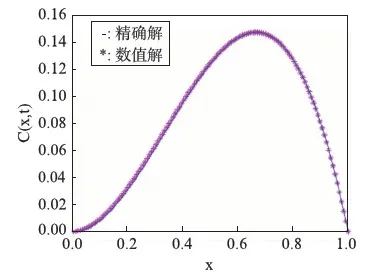
3 多参数联合反问题与反演算法

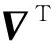


4 数值反演
4.1 精确数据下的反演





4.2 扰动数据下的反演



5 结 语
