基于电压空间矢量算法的伺服系统

张洪国，董瑞佳，赵 辉,徐世英

(唐山工业职业技术学院 a.自动化工程系； b.大数据中心，河北 唐山 063200)

基于电压空间矢量算法的伺服系统

张洪国a，董瑞佳a，赵 辉a,徐世英b

(唐山工业职业技术学院 a.自动化工程系； b.大数据中心，河北 唐山 063200)

通过导弹舵机交流化提高舵机的工作效率、控制可靠性及功率密度，达到弹体轻型化、小型化的目的。为使导弹舵机交流伺服控制器具有谐波含量少、高频噪声小的正弦电流波形输出，引入了电压空间矢量(SVPWM)算法，并建立了基于SVPWM算法的扇形区判断算法及PWM波生成函数。提高了导弹舵机交流伺服系统的控制性能。通过实验验证了方案的可行性，最终通过参数对比得到了满足导弹舵机工作要求的交流伺服系统。

电压空间矢量；查表；高速；舵机

导弹作为现在战争中的精确打击武器，在现代战争中的地位越来越重要。导弹之所以能够精确制导是因为其在打击过程中不断地利用舵机进行弹道的修正，舵机电机通过减速器控制舵面的旋转不断修正弹体的飞行姿态，最终实现精确制导、远程打击的目的。新形势的作战环境下，导弹舵机仍存在能源利用率低，体积大，控制可靠性低、功率密度小等缺点。而交流永磁电机相对于直流电机具有结构简单、可靠性高、效率高、功率密度大等优点，实现导弹的轻型化、小型化，使导弹具有更远的射程。本文提出的基于电压空间矢量(SVPWM)算法的导弹舵机伺服控制系统有效地抑制了输出信号的谐波含量和高频噪声，提高了舵机的控制性能及控制精度。利用交流伺服控制系统的引入提高了舵机的功率密度、工作效率。

1 空间矢量算法的实现

永磁同步电机的控制过程可以简单地理解为由永磁同步电机的定子三相绕组电流产生的旋转磁场吸引转子的磁极进而带动转子运动。旋转磁场的产生及控制是通过控制交流永磁同步电机的三相定子绕组电流及电压来完成的。

电压空间矢量算法的实现首先要得到旋转电压矢量与旋转磁场的关系，建立扇形区判断函数及表格，进而判断系统本周期输出电压空间矢量的相位，最终利用八种基本电压空间矢量的时间线性组合表示任意时刻的系统输出电压空间矢量。

1.1 电压矢量和磁链矢量的关系

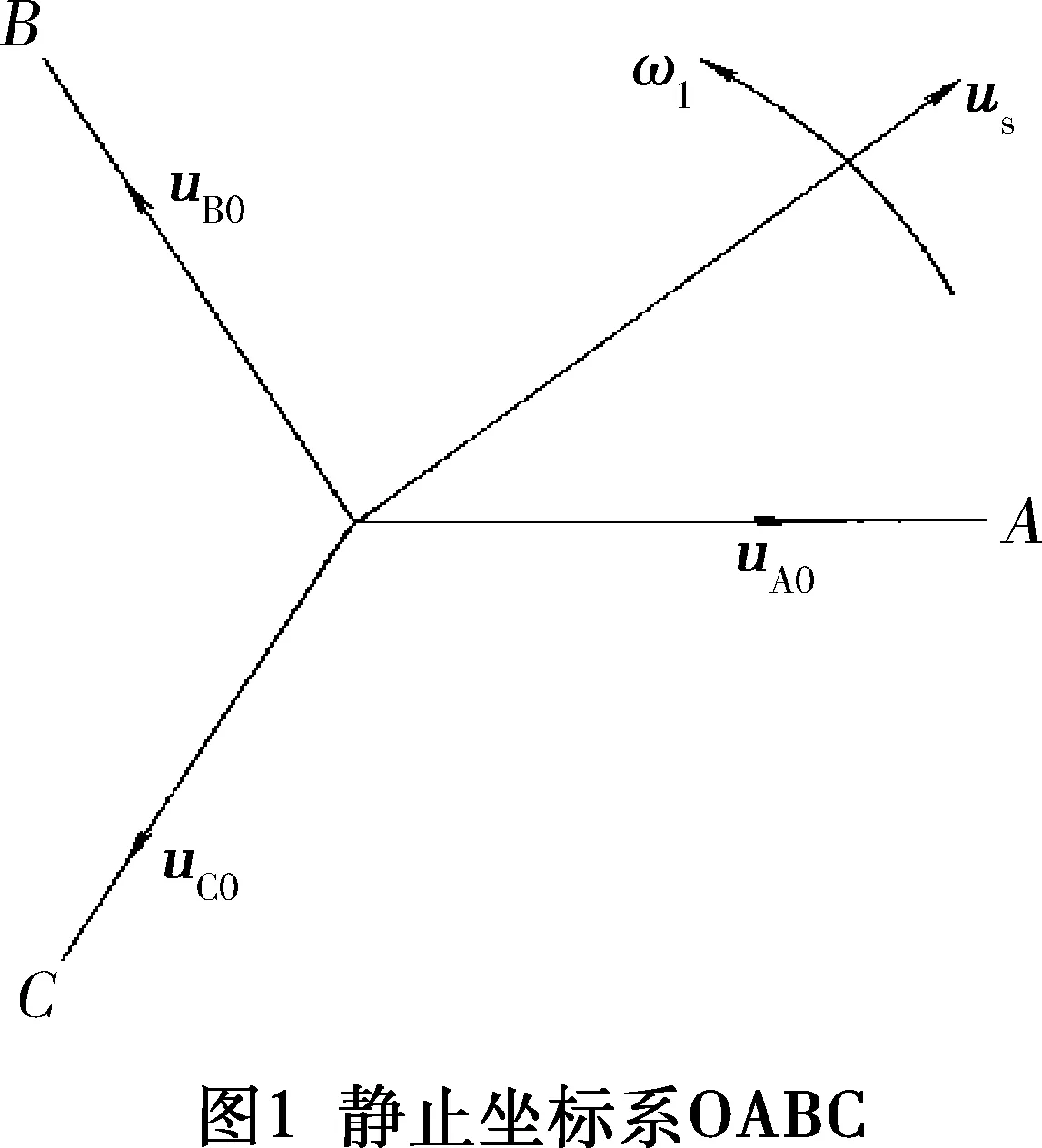
首先，在永磁同步电机的定子绕组上建立一个静止坐标系OABC(见图1)，令这个静止坐标系所在平面与电机转子的轴线垂直，坐标的原点在交流永磁同步电机的转轴轴心上，静止坐标系的A、B、C三个坐标轴分别与同步电机的三相定子绕组的轴线重合。

在永磁交流电机的工作过程中，交流永磁同步电机各相相电压的电压幅值和极性都随其工作时间呈正弦变化。因此，交流永磁同步电机各相定子绕组可以用空间矢量描述，且矢量方向均在A、B、C坐标轴上。

则三相定子绕组的合成电压矢量为：

us=uA0+uB0+uC0

(1)

由式(1)可知，合成电压空间矢量是一个以电源角频率旋转的空间矢量。同理可得电流合成空间矢量Is。同样定义合成磁链空间矢量为：

Ψs=ΨA0+ΨB0+ΨC0

(2)

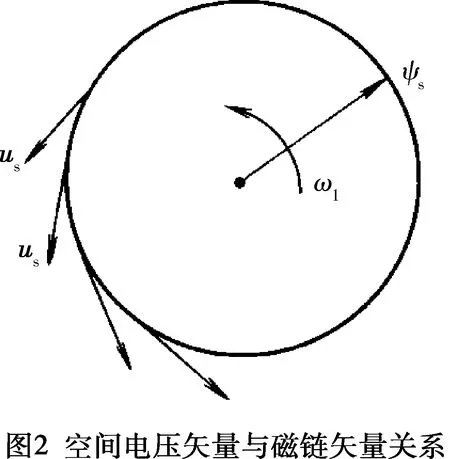
交流永磁同步电机在工作过程中由式(2)可知合成磁链空间矢量大小不变，其矢量方向以电源角频率旋转。由此可知，合成磁链空间矢量的矢端的运动轨迹是一个以其幅值为半径的圆(见图2)，称为磁链圆。故三相定子的合成磁链空间矢量可表示为：

Ψs=Ψmejωt

(3)

利用合成电压空间矢量表示的三相永磁交流电机定子绕组的电压方程式为：

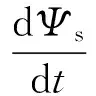
(4)

式(4)中us为定子三相电压合成空间矢量；Is为定子三相电流合成空间矢量；Ψs为子三相磁链合成空间矢量。

通常情况下，定子绕组的电阻比较小，因此定子绕组上的压降也比较小。此外，在电机转速不是很低时，由于旋转角频率很大，导致定子绕组压降在电压矢量所占比例非常小，故子绕组的压降可以忽略不计，(4)化简为：

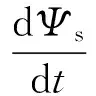
(5)

联立(4)与(5)可得：

(6)

由式(6)可知，合成磁链空间矢量的幅值Ψm一定时，合成电压空间矢量us的大小与电机转速ω成正比例关系。合成电压空间矢量的相位超前于合成磁链空间矢量90°相位角。由此可知，通过控制伺服控制器来完成电压空间矢量的旋转即可完成对磁链空间矢量的控制，从而使控制对象得到精确稳定的控制。

1.2 圆形旋转电压矢量的实现

β计算得到该控制周期所需要输出的电压信号进而控制IGBT开关时间及时序，从而产生逼近圆形的旋转磁场的一种方法。

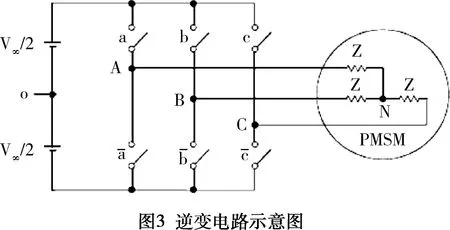
图3为简单的电压型PWM逆变电路的示意图，合理的控制该逆变电路功率开关管的开关状态，开关时间以及开关顺序即可使电压空间矢量的运动轨迹为圆形。

逆变电路中若上桥臂IGBT开启用“1”表示，关闭用“0”表示。此时逆变电路中的a，b，c三个桥臂可以形成八种逆变器IGBT开关模式即[111]，[110]， [101]，[100]，[011]，[010]，[001]，[000]。

由图3可知：

(7)

式中：i1为线圈a的电流；i2为线圈b的电流；i3为线圈c的电流；Z为各相线圈的阻抗。

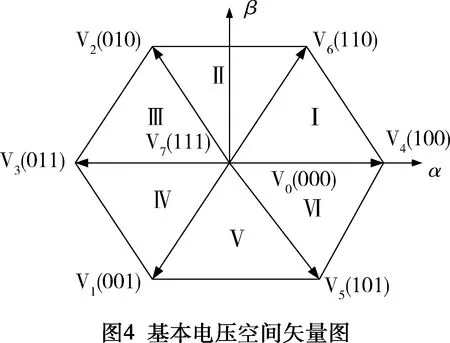
由八种逆变器的开关状态可以得到两个零矢量及六个基本矢量，见图4。

由图4可知，当控制器逆变电路开关状态为[100]时，永磁交流电机的定子磁链矢量s的矢量端点将由A向B沿平行于α轴的方向移动。以此类推，则最终的矢量矢端轨迹为图4所示的正六边形。

这样的供电方式只能形成正六边形的旋转磁场，设想将每个扇区再分成若干小区间，则当区间数量很多，区间所占角度很小时，正多边形磁场将逐渐逼近圆形磁场。故将图4中六个基本电压空间矢量所组成的扇形区进一步细分为N个扇区，则整个电压空间矢量平面被分为6N边形来逼近正圆轨迹，进而得到永磁交流电机的定子磁链矢量Ψs为圆形旋转磁场的目的。

1.3 扇形区判断方法

在进行SVPWM控制算法进行调制时，首先要计算并判断合成电压空间矢量Vsref位于哪个扇区，再利用扇区两侧的基本电压空间矢量及零矢量来合成所需要的电压矢量Vsref。

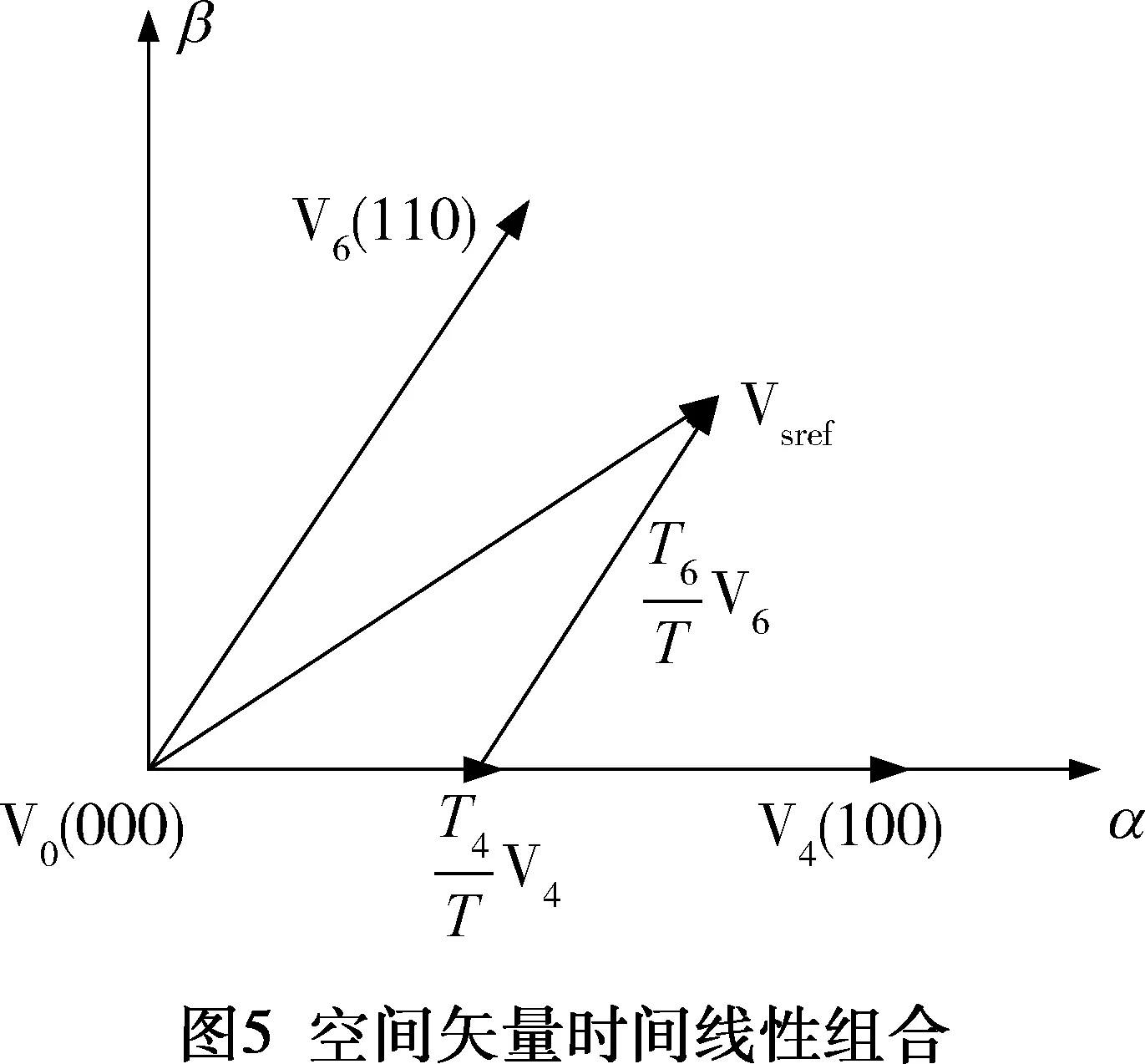
完成空间矢量算法的第一步首先要判断由Vα和Vβ决定的合成电压空间矢量Vsref所处的扇形区位置。

若合成电压空间矢量Vsref落在第一扇形区，则由图5可知，Vα和Vβ必须满足如下条件：

(8)

同理可得落在其他扇形区时的Vα和Vβ条件，由落在各扇形区的条件可知，合成电压空间矢量Vsref落在某个扇形区内的制约条件与Vα和Vβ的线性组合有关。

当Vsref以α-β静止坐标系上的分量形式Vαref，Vβref给出时，假设以下辅助函数:

(9)

S=sign(G0)+2sign(G1)+4sign(G2)

(10)

其中sign(x)为符号函数，若内部数值为正数则sign(x)=1，若内部数值为负数则sign(x)=0。

根据图5及其制约条件可得合成电压空间矢量所在扇形区与S值的对应关系表，即表1。

表1 函数值与扇形区对应关系

1.4 基本电压空间矢量作用时间的计算

如图5所示，若合成电压空间矢量落在第一扇形区Vsref是期望输出的合成电压空间矢量。则Vsref可以表示为：

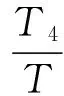
(11)

其中的T4和T6分别为V4和V6的作用时间。T为Vsref的作用时间。当控制周期T很小时，此时正多边形变数将很多从而能很好的逼近圆形旋转磁场。由正弦定理可得：

(12)

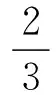
(13)

若假设合成空间矢量Vref落在任意扇形区，并将扇形区两侧的基本电压空间矢量记为Vx和Vx+60，其中作用时间分别为Tx和Tx+60，且Vref与Vx夹角记为θ。则根据第一扇形区类推可得：

(14)

式中：T由控制过程中的PWM控制周期给定，θ可由输出电压的角频率和nT确定。

通常情况下T与Tx+Tx+60并不相等，其间隙时间一般令V7和V0各占一半，因此T7与T0分别为：

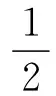
(15)

在实际控制过程中为使逆变电路输出的PWM波对称一般会将每个基本矢量的作用时间一分为二，采用如下七段式PWM波生成方案，各基本空间矢量作用顺序为：

V000，Vx，Vx+600，V111，Vx+600，Vx，V000

作用时间分别为：

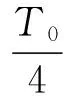
有以上对空间电压矢量算法的分析可知，算法的实现为：首先根据静止两相电压Vα和Vβ通过辅助公式(10)得出S值，通过S值查表(1)判断出合成电压矢量Vref所在的扇形区，由所在扇形区确定Tx和Tx+60，进而通过公式(13)、(14)得到各个基本电压空间矢量的作用时间。从而生成合理的PWM波。

2 实验结果

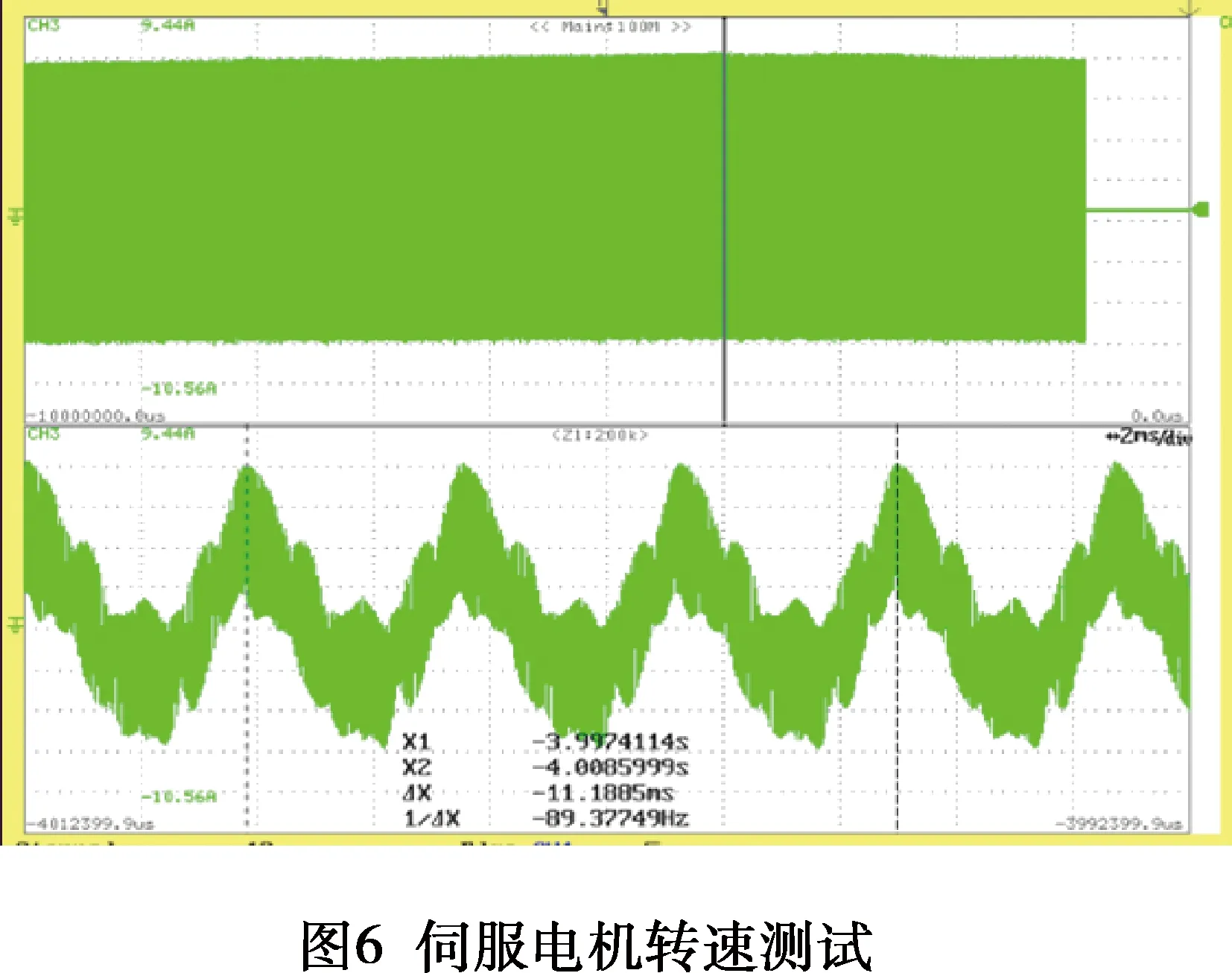
图6所示为转速为16 200转时的U相电流，此时输入电流为5 A，电源模块供给母线电压为50 V。由图中可以看出U相电流波形为正弦波且无电流过冲和发散的现象。电机在16 200转可以正常运行，故系统可以实现高速控制。

本实验的定位精度试验是通过将高精度光电编码器与被测试系统伺服电机同轴安装，测试过程中通过伺服指令对交流伺服电机进行定位待其稳定后将稳定的转子角度位置通过高精度的光电编码器进行输出。通过多次固定位置角度输出得出伺服控系统的定位精度。

由图7为伺服控制系统定位测试实验中通过高精度光电编码器得到的转子角度位置信息。由图7中可以看出伺服控制系统定位精度可以达到±0.1°。

3 结论

当前导弹舵机舵轴最大输出转速一般250 °/s。舵面角定位精度为±0.1°。舵机减速器减速比一般为5～200之间。由本次试验实验结果可知，本次交流伺服系统可在16 200 r/min下稳定运行，且控制精度控控制在±0.1°。舵机减速器减速比一般为5～200之间，通过最不利于交流伺服系参数的转化方式可知若要求导弹舵机舵轴最大输出转速一般250 °/s。舵面角定位精度为±0.1°。

此时对交流伺服控制系统的最高要求为：

R=2500×60×200/360=8333r/min
Δθ=±0.10×5=±0.50

由以上两式可知，舵机对伺服控制系统的要求参数均小于本次实验所得到的结果。

故本系统可以满足导弹舵机的精度性能要求。

[1] Van Der Broeck H W, Skudelny H C, Stanke G V. Analysis and realization of a pulsewidth modulator based on voltage space vectors[J]. Industry Applications, IEEE Transactions on, 1988， 24(1): 142-150.

[2] 姚霞. 空间电压矢量 PWM 过调制控制方法的研究[J]. 科技信息, 2010(23): 10097-10098.

[3] 钟宇明, 文励洪, 杨红, 等. 三相电平电路空间矢量调制的一种新算法[J]. 电力电子技术, 2010(1): 90-92.

[4] 戴宁怡, 黄民聪, 唐净, 等. 新型三维空间矢量脉宽调制在三相四线系统中的应用[J]. 电力系统自动化, 2003, 27(17): 45-49.

[5] 吴茂, 刘铁湘. 空间矢量脉宽调制技术研究[J]. 现代电子技术, 2006(2): 06.

ServoSystemBasedonVoltageSpaceVectorAlgorithm

ZHANG Hong-guoa， DONG Rui-jiaa， ZHAO Huia, XU Shi-yingb

(a.Department of Automation Engineering; b.Big Data Center, Tangshan Polytechnic College,Tangshan063200， Hebei, China)

Through the exchange of missile steering servo to improve work efficiency, reliability and power density control to achieve lightweight airframe, miniaturization purposes. For the output of the sinusoidal current waveform, which has less harmonic content, high-frequency noise in the AC servo controller, a voltage space vector algorithm was performed in this paper. And due to the SVPWM algorithm, a fan-shaped area decision algorithm and PWM wave generating function were brought in. Thus, it improves the performance of control further. Experiments showed the feasibility and met the work requirements of missile servo AC servo system by parameter comparison.

voltage space vector; meter inspection; high speed; steering gear

2017-04-10

张洪国(1989-)，男，山东德州人，工程师，研究方向为自动化控制技术，E-mail：hgzhang1989@126.com。

V42

A

1008-9446(2017)06-0055-05