稳态法水平井产能模型评价与对比

武延鑫，董长银，高凯歌

(中国石油大学(华东) 石油工程学院，山东 青岛 266580)

稳态法水平井产能模型评价与对比

武延鑫，董长银，高凯歌

(中国石油大学(华东) 石油工程学院，山东 青岛 266580)

针对不同稳态法水平井产能计算模型的假设条件、推导方法各有不同，导致其产能计算结果存在较大差异的问题，选择合适的模型应用于不同影响因素下水平井产能的计算，在综述国内外多种水平井产能模型的基础上，通过算例计算，评价各模型对产能预测结果的精确程度，并对其计算结果的差异性进行分析，讨论了水平井两端边界对产能预测的影响；引入水平井无因次拟表皮系数的概念，分析各不同影响因素下各类模型对产能预测结果的敏感程度。结果表明，Joshi模型、Renard-Dupuy模型、郎兆新模型、陈元千模型对渗透率非均质性小于1时的情况其产能计算结果有较好的一致性， Renard-Dupuy模型对渗透率非均质性大于1的情况适用性较差；徐景达模型和窦宏恩模型弱化了水平井两端供给区域的影响，因此其对长水平井的情况较为适用。

水平井；产能模型；影响因素；对比分析；稳态

稳态法水平井产能模型是水平井产能计算的一种有效工具[1]。目前，国内外众多水平井稳态法产能模型具有不同的公式结构和适用条件[2-9]，且对各产能影响因素的敏感程度不同[10-15]，导致难以选择合适的水平井产能模型应用于实际计算。笔者针对上述问题，选择常用的几种水平井稳态法产能模型，通过算例计算，对比各模型对水平井产能的预测效果；分析各产能模型对不同水平井产能影响因素的敏感程度。从而为选取合适的水平井稳态法产能模型应用于实际计算提供有价值的参考意见。

1 水平井稳态法产能模型

目前针对于水平井产能的描述主要有稳态法和拟稳态法两种。常用的水平井稳态法产能模型如下：

Joshi模型[2]，利用拟三维的研究方法，将水平井的三维渗流转变为水平面和垂直面的二维平面渗流问题。其模型为椭圆供给边界，考虑渗透率非均质性、水平井偏心距：

(1)

Renard-Dupuy模型[3]，基于Joshi产能公式的基础上，考虑水平井近井地带储层伤害，给出了稳态水平井产能方程的修正模型。其模型为椭圆供给边界，考虑渗透率非均质性：

(2)

郎兆新模型[4]，利用拟三维方法，通过保角变换将水平面长度为2L的导流裂缝的渗流场转化为宽度为π的无限长一维流动。其模型为椭圆供给边界，考虑渗透率非均质性、水平井偏心距：

(3)

陈元千模型[5]，利用面积等值的拟圆形驱动半径和产量等值的拟圆形生产坑道的物理概念，将椭圆驱动边界等效为圆形驱动边界，将水平井段等效为圆环状生产坑道。分别计算两部分渗流阻力。其模型为椭圆供给边界，考虑渗透率非均质性、水平井偏心距：

(4)

徐景达模型[6]，考虑Joshi模型两端供给边界无限远的极端情况，给出了修正的水平井产能模型。其模型为矩形供给边界，其与Joshi模型计算值的平均值为最终产能计算结果：

(5)

窦宏恩模型[7]，利用镜像反映原理，将水平井视为无限大地层中一口垂直井。其模型为矩形供给边界，考虑渗透率非均质性、水平井偏心距：

(6)

符号说明：PI为水平井产能，m3/(MPa·d)；μo为地层原油粘度，mPa·s ；Bo为地层原油体积系数，m3/m3；kh为水平渗透率，μm2；kv为垂直渗透率，μm2；K为平均渗透率，μm2；β为渗透率各向异性系数(无量纲)；h为储层厚度，m；L为水平井长度，m；a为椭圆半长轴，m；δ为水平井偏心距，m；re为驱动半径，m；reh为等价驱动半径，m；rw为井筒半径，m；rwe为有效井筒半径，m；S为拟合表皮系数(无量纲)。

2 不同稳态法产能模型对比

2.1 稳态法水平井产能计算

采用文献[7]某油田水平井产能计算算例对稳态法水平井产能公式计算结果进行比较[7]，数据见表1。

表1 水平井产能算例基础数据

经计算，各稳态水平井产能结果汇总于表2。

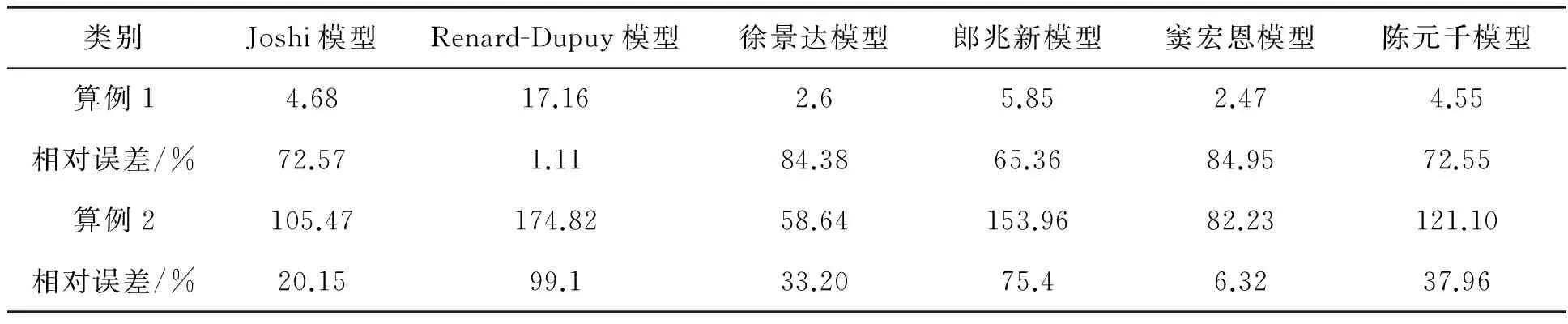
表2 稳态法水平井产能计算结果 (单位：m3/MPa·d)

对比表2计算结果相似性，将Renard-Dupuy、郎兆新模型记为a类模型；Joshi、陈元千模型记为b类模型；将徐景达、窦宏恩模型记为C类模型。

2.2 稳态法水平井产能模型计算结果差异性分析

a，b两类模型假定供给边界为椭圆形。两类公式计算差异的原因在于b类模型较a类模型公式分母第二项缺少一π项。

c类模型假定供给边界为矩形。徐景达认为，a，b两类模型将水平井供给区域看做椭圆是一种理想情况，该情况下水平井供给面积最小，在同一生产压差作用下，其计算结果要大于实际产能，并提出实际水平井的供给区域应当介于两端无限长的矩形与理想椭圆之间(见图1)。窦宏恩利用镜像反应原理将供给边界视为无限长矩形。可认为c类模型实际上是弱化或忽略了水平井两端供给边界的影响，这种假设对于长水平井更为适用。

3 不同稳态法产能模型对各影响因素敏感程度

根据上节讨论，为探究a，b两类模型的选用策略，通过计算水平井拟表皮系数，对比各模型拟表皮系数在不同产能影响因素下的变化规律。为便于计算，将Joshi和陈元千对水平井偏心距的表达方法用于Renard-Dupuy公式；将Muskat对非均质性的讨论方法[8]应用于郎兆新公式。

水平井拟表皮系数用于描述水平井相对于垂直井的产能增加程度[15]。如式7所示，S为拟表皮系数，rwe为有效井眼半径。S应为负值，且绝对值越大，水平井相对于垂直井产能越高。

(7)

在给定的供给半径和井筒半径下，影响水平井拟表皮系数的因素主要为水平井长度L，水平井厚度h，渗透率非均质性β，水平井偏心距δ。

3.1 储层厚度和渗透率非均质性对拟表皮系数的影响

渗透率非均质性用来描述储层水平方向和纵向上渗透率差异，由于垂向渗透率主要影响水平井垂直面的渗流，因此非均质性对产能的影响还可能与储层厚度有关。因此给定一系列储层厚度(h=10 m，50 m，100 m)，和一定的非均质性范围(β=0.1～0.2)，定量分析非均质性对四种水平井拟表皮系数的影响，取L=300 m，δ=0 m，rw=0.1 m，re=170 m，计算四种拟表皮系数并做其随渗透率非均质变化的曲线见图2。

由图2可以看出：1)四种模型在β<1时的拟表皮系数有较高的一致性；2)β>1时，四种模型的拟表皮系数计算结果差异随β增加逐渐加大；3)储层厚度越大，β对拟表皮系数的影响程度越大。说明储层厚度增大会加剧β对水平井产能的不利影响。

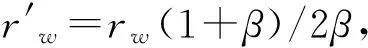
3.2 水平井偏心距对拟表皮系数的影响

水平井偏心距用于表示水平井偏离油层中心的距离。对于水平井在油藏中所处的空间状态可以通过偏心距、水平井长度和储层厚度来描述，因此偏心距对水平井拟表皮系数的影响可以通过偏心比 2δ/h和水平井长度与储层厚度之比L/h的关系来体现。给定一系列长厚比L/h=6/12/30和偏心比(2δ/h=0.2、0.4、0.6、0.8)，定量分析偏心距对四种水平井拟表皮系数的影响，取L=300 m，h=10 m，15 m，20 m，β=1，rw=0.1 m，re=170 m，计算四种拟表皮系数并做其随偏心比变化的曲线见图3。

由图3可以看出：1)L/h越大，四种水平井拟表皮系数计算结果差异越大，但不同拟表皮系数间的差异随2δ/h的变化较为稳定，说明四种模型对水平井偏心距的敏感性较为一致。2)偏心距相对于渗透率非均质性对水平井拟表皮系数的影响较小。

4 结论与认识

1)Renard-Dupuy模型、郎兆新模型与Joshi模型、陈元千模型产能结算结果的差异在于公式结构中有无π项的争议。通过算例计算验证，对于不同产能计算前提下无π项的模型计算结果反而更为精确。

2)渗透率非均质性是影响水平井产能计算的主要因素。非均质性小于1 时，Joshi模型、Renard-Dupuy模型、郎兆新模型、陈元千模型的产能计算结果有较好的一致性，而Renard-Dupuy模型对渗透率非均质性大于1的情况适用性较差。

3)徐景达模型、窦宏恩模型将供给边界视为矩形，实际上是弱化或忽略水平井端部供给区域的影响，这种假设对于对长水平井的情况更为适用。

[1] 叶春芳.水平井产量计算公式探讨[J].钻采工艺，1994(7):50-54.

[2] S.D.Joshi. Augmentation of Well Productivity With Slant and Horizontal Wells[R]. SPE.15375,1986.

[3] Gerard Renard,J.M.Dupuy. Formation Damage Effects on Horizontal-Well Flow Efficiency[J]. SPE-19414,1991.

[4] 郎兆新.多井底水平井渗流问题某些解析解[J]. 石油大学学报(自然科学版),1993(4):40-47.

[5] 陈元千.水平井产量公式的推导与对比[J]. 新疆石油地质, 2008(1): 68-71.

[6] 徐景达.关于水平井的产能计算——论乔希公式的应用[J]. 石油钻采工艺,1991(6):67-74.

[7] 窦宏恩.预测水平井产能的一种新方法[J].石油钻采工艺,1996(1)：76-81.

[8] P.N.Mutalik. Effect of Drainage Area Shapes On The Productivity Of Horizontal Wells.SPE-18301,1988.

[9] 陈元千.水平井产量公式的对比研究[J],2012(5)：566-569.

[10] 高海红,王新民.水平井产能公式研究综述[J]. 新疆石油地质, 2005(6):121-124.

[11] 袁淋.水平井稳态产能公式对比与分析[J]. 岩性油气藏, 2013(6):127-132.

[12] 单保超,付玉.关于水平井产量公式的讨论与分析[J]. 新疆石油地质, 2015(5):624-628.

[13] 胡东晖, 郡捷年.水平井产能的影响因素[J].石油勘探与开发,1994(5)：44-52.

[14] 陈元千.考虑各向异性和偏心距影响的水平井产量公式推导_对比与应用[J].新疆石油地质,2009(4)：487-489.

[15] 陈元千. 确定水平井产能比、流动阻力比、驱动面积比和表皮因子的新方法[J]. 中国海上油气, 2009(3):165-168.

EvaluationandComparisonofSteadyStateHorizontalWellProductivityModels

WU Yan-xin, DONG Chang-yin, GAO Kai-ge

(Petroleum Engineering Institute, China University of Petroleum (East China),Qingdao266580, Shandong, China)

The assumptions and derivation methods of steady state horizontal well productivity calculation models are different, which leads to the large difference in the calculation results. To facilitate the selection of suitable models for researchers applied in different production influencing factors, this paper summarizes various production models home and abroad, evaluates the accuracy of each model by giving numerical examples, and analyzes the reason which causes the difference of the results. The results show that Joshi model, Renard-Dupuy model, Lang Zhaoxin model and Chen Yuanqian model are better used in the case, and the heterogeneity permeability is less than1. Renard-Dupuy model is not suitable for the case, and the heterogeneity permeability is more than1; Xu Jingda model and Dou Hongen model weaken the influence of the supply area at both ends of the horizontal well, so it is more suitable for the long horizontal wells.

horizontal wells; productivity model; influencing factor; comparison analysis; steady state

2017-03-20

武延鑫(1993-)，台湾台南人，硕士研究生，现从事采油理论、防砂完井方面的研究工作，E-mail:wuyanxin1993@163.com。

TE32

A

1008-9446(2017)06-0001-05