借助几何直观 促进数学思考

吴丽琴

（福建省莆田市城厢区教师进修学校，福建莆田 351100）

借助几何直观 促进数学思考

吴丽琴

（福建省莆田市城厢区教师进修学校，福建莆田 351100）

几何直观是影响中小学生数学发展的重要因素之一，培养和发展学生的几何直观，是数学课程的核心目标之一。本文主要结合具体案例，对几何直观在数学教学中的应用进行分析，深入挖掘了感知模型、抽象模型、逆用模型三项几何直观建模路径，希望为小学数学教学效益的改善提供一定的参考。

小学数学；几何直观；数学思考

引 言

小学生思维还不成熟，在数学学习的过程中往往无法理解复杂和奥妙的数学关系，这在一定程度上影响了他们的学习效益。几何直观可以将抽象的数学概念具体化，大大降低了小学数学学习的难度。它不仅能够实现学生几何直观能力的提升，还能够将学生的逻辑思维和形象思维全面融合，促进学生进行数学思考，为学生数学学习奠定良好的基础。

一、感知模型，了解基本内容，让学生“愿思”

感知模型主要指在小学数学教学的过程中借助学生熟悉的事物和场景，提炼出与之相符合的数学模型，化未知为已知，化陌生为熟悉，从而提升学生对小学数学概念的理解和认识。笔者在小学数学教学的过程中非常注重感知模型的构建，往往借助生活原型为学生构建几何直观，引导学生感知模型，在该基础上解决数学问题。与此同时，笔者还鼓励学生让其自己寻找容易记忆和容易理解的几何模型，让其自己在建立模型的过程中加深对概念内容和概念关系的感知，达到了事半功倍的效果。

如在《乘法交换律》教学的过程中，笔者首先让学生自学本节的概念，并结合课本分析为什么a×b=b×a。学生自学完成后，笔者与学生交流时发现很多学生都只是了解了概念，但并不能够指出为什么乘法交换律成立。为此，笔者借助模型直观，让学生在几何模型基础上直接感知这一等式的内容（见图1）。在该图形下，学生对乘法交换律的认识更加深入，课堂教学效益明显提升。课堂教学完成后笔者还鼓励学生让其结合自己所了解的内容，再构建几个乘法交换律的几何模型。该教学完成后，学生对数学概念的掌握更加全面，几何模型构建能力明显改善。

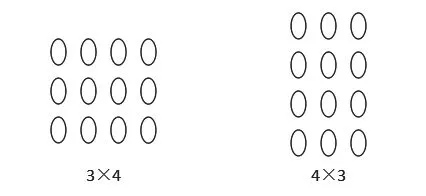
图1 乘法交换律的几何直观模型

感知模型时教师需要把握好几何直观的引导，让学生能够结合模型直观地、更加深入地认识概念和理论，这是小学数学教学中的关键。要多从贴近学生生活的事物和学生感兴趣的事物出发构建几何直观模型，让学生能够高效感知，这样才能够从根本上激发学生数学学习的主观能动性，使他们“愿思”。

二、抽象模型，把握要点核心，让学生“会思”

几何直观涉及范围非常广泛，如何形成高效、科学的小学数学几何直观模型一直是教师工作的重中之重。借助几何直观开展小学数学教学时，仅仅通过感知模型只能够让学生了解初步的概念体系，对数学知识有一定的认识，但并不能让学生一举中的，准确地把握数学知识的重点和核心。因此，教师需要对几何直观进行调整，让具体的模型抽象化、复杂化，从而引导学生从多方面思考问题，运用不同的手段解决问题，为学生数学思维的培养创造良好的环境。

如在《乘法分配律》教学的过程中，笔者引导学生感知模型（见图2）后询问学生：“当边长增加了30m后，你们知道图中草坪面积增加了多少吗？在这种状况下图中草坪的总面积变成了多少呢？同学们理解乘法分配律公式了吗？”

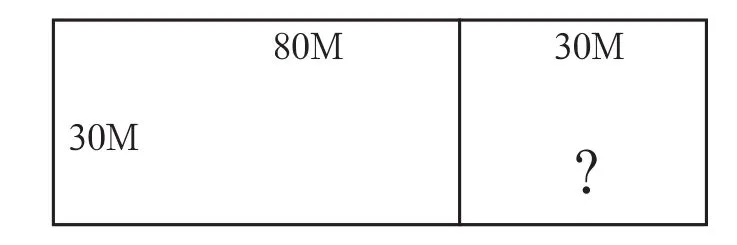
图2 乘法分配率的几何直观模型1

在学生回答理解后，笔者将几何直观模型转变为下述模型（见图3），让学生分析这两个几何直观模型有什么异同，引导学生将下述模型展现的特征代入图2中，验证自己的猜想是否成立。

图3 乘法分配律的几何直观模型2

小学数学教学过程中几何直观模型的抽象化要求从不同的角度、不同的方面诠释数学概念，用不同的几何直观展现知识内容，让学生大胆猜想并进行验证，从而得到具有普适性的数学模型。这种对等处理和模型抽象的过程不仅能够让学生全面认识数学概念核心，还能够让学生将数学知识“玩弄于股掌之间”，使他们“会思”。

三、逆用模型，加深知识理解，让学生“善思”

许多学生在数学学习的过程中都存这样的问题——直接运用数学概念处理数学问题感觉非常顺手，但逆用数学概念解决问题却无从着手。这主要是由于学生对数学概念的逆向认识和运用不到位，在教学的过程中需全面重视。逆用模型能够从根本上改善学生学习效果。逆用模型时，教师可以借助熟悉的数学模型，将其逆用，通过尝试计算、头脑想象、动手操作、总结分析，让学生全面把握数学概念，提升数学解题能力。

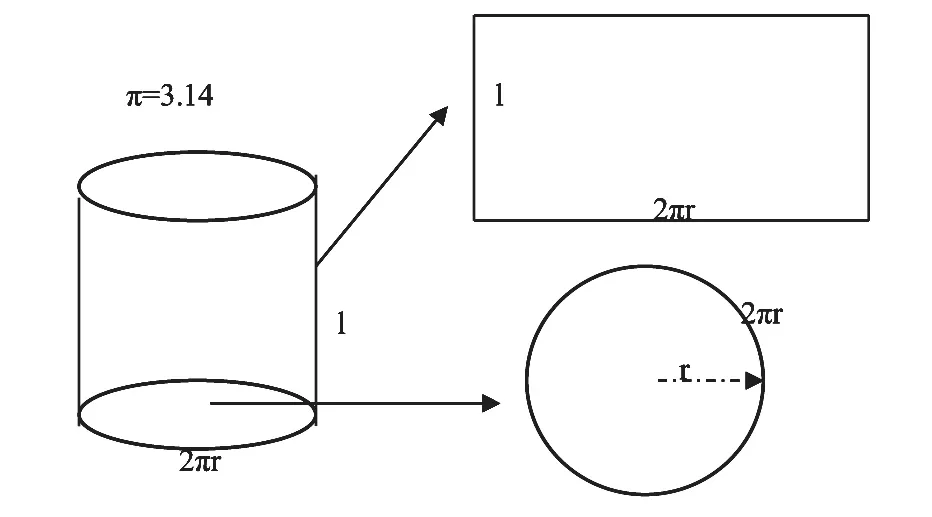
如在教学《圆柱的底面积与侧面积》的过程中，笔者就设计了圆柱体几何直观的逆用（见图4）。在该基础上提出问题：“同学们，你们既然已经知道了如何用圆柱的半径和高求圆柱的侧面积，那么当圆柱体的高为2m，侧面积为6.28m2，圆柱的底面积是多少呢？你们能够通过该几何直观模型快速、准确地给出答案吗？”在上述引导后，学生依照数学概念的逆用几何直观模型直接说出答案都是3.14m2，对圆柱底面积和侧面积之间的关系有了更深刻的认识，逆向运用解决数学问题的效果明显提升。

逆用模型是培养学生逆向思维的关键。在该教学的过程中教师要学会几何直观模型的逆向考虑和教学，让学生结合该模型解决数学问题，将逆向模型与数学实践融合在一起，潜移默化中培养学生的逆向思维，提升学生对数学问题的处理能力，使他们“善思”。

结 语

小学数学教学的过程中教师要把握好几何直观模型的构建，依照数学概念内容及概念之间的关系对几何直观模型进行适当调整，让学生从不同方面、不同角度理解数学知识点，确保学生能够熟练掌握课堂教学的重点和难点，促进数学思考，培养学生数学思维，让学生能够快速、高效地解决数学问题，从根本上提升小学数学教学质量。

[1]冷洪涛.小学数学教学要与生活实际相结合［J］学周刊：B，2012（8）：1.

[2]边会发.数学教学要注重数学思想方法的渗透［J］.中国教育技术装备，2010（13）：1.

[3]周峰.中职生物教学中培养学生逆向思维的研究［J］.时代教育，2015（8）：1.

吴丽琴，1972年生，女，福建莆田人，莆田市城厢区教师进修学校小学数学教研员，莆田市小学数学学科带头人，莆田市吴淑红名师工作室核心成员。