非结构网格流线快速可视化方法

贾志强

(中国石油大学胜利学院 网络信息中心,山东 东营 257000)

矢量场可视化是科学可视化的重要分支,在油气田油层分析、气象预报、海洋数值模拟等领域都有着广泛的应用[1]。流线可视化是目前矢量场可视化中应用最广泛的方式之一,是业务人员分析矢量场最重要的工具。此外,流线还是很多其他可视化方式(如LIC、FTLE等)的基础,受到了可视化领域广泛的关注。随着数据规模的不断增大,流线可视化的效率逐渐成为大规模矢量场数据快速可视化处理与分析的瓶颈。为此,许多学者致力于高效流线可视化方法的研究。目前通常的方法是采用并行加速技术,利用计算机集群或者超级计算机,对流场数据和可视化任务进行划分后分派给各个节点,多个节点同时进行计算。流线并行主要有数据块并行和种子点并行两种方式。数据块并行的典型方法有:Nouanesengsy等[2]提出的负载敏感数据划分策略、Sujudi等[3]提出的空间分解方法等;种子点并行的典型方法有:Chen等[4]提出的最优化动态数据划分策略、Chen等[5]提出的空间一致性方法等。此外,彭宝云等[6]以及Zhang等[7]利用数据预取技术进行流线高效可视计算的方法。以上方法虽然从各种角度对流线可视化过程进行加速,但是在流线生成过程中都是利用数值积分进行计算。针对该问题,笔者首先利用代数运算将流线表示成矩阵形式,进而将流线在网格单元内的积分运算转化成矩阵表示的方程与网格单元各表面求交点的问题,并利用牛顿迭代法进行求解,从而避免繁琐的数值积分运算,有效提高大规模矢量场流线可视化的效率。

1 非结构网格的流线矩阵表示

对于矢量场中的流线,可以看成是如下微分方程的解:

对于大规模科学与工程计算中最常用的线性矢量场,可以将其表示成如下的形式:

v(x)=Ax+b.

非结构网格由于其表达的灵活性,目前得到越来越广泛的应用。四面体网格是应用最广泛的非结构网格,且任意的结构网格和非结构网格都可剖分为四面体网格,故本文中处理四面体网格线性流场。

由常微分方程的理论可知,四面体网格线性流场条件下,微分方程(1)的解可表示为

x(t)=e(t-t0)Ax0+(e(t-t0)A-I)A-1b.

(2)

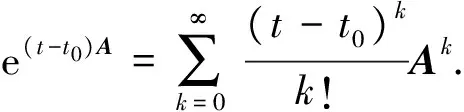
为了得到流线方程(2)的表达式,将矩阵A进行特征值分解。利用线性代数知识可以证明,当A有3个不同的非零实特征值,或者两个复数特征值、一个非零实特征值时,流线方程(2)都可以表示成如下的形式:

x(t)=SP(t)S-1x0+SQ(t)S-1b.

(3)

式中,矩阵S是A的3个线性无关的特征向量组成的矩阵(由于A有3个不同的特征值,故必有3个线性无关的特征向量);当A有3个不同的非零实数特征值时(分别用λ1、λ2和λ3表示),矩阵

当A有两个复数特征值、一个非零实特征值时,利用线性代数知识可推导出类似的P(t)和Q(t)的表达式。

需要说明的是,虽然推导过程看似繁琐,但由于上述矩阵都是三阶矩阵,其计算过程并不耗时,且可在预处理阶段计算,得到的各矩阵当作每个网格单元的属性进行存储。后续进行流线可视化处理与分析时,各矩阵无需再次计算。

2 非结构网格的流线可视化方法

2.1 网格单元分类

根据各网格单元矩阵的特征值,将非结构四面体网格单元分为3类:

(1)平行单元。4个网格顶点的矢量值完全相同;(2)普通单元。网格单元矩阵具有3个非零的实特征值,或有两个复数特征值和一个非零的实特征值;(3)其他单元。除以上两种情况外的其他网格单元。

2.2 网格单元处理形式

对应上述3种情况,分别进行如下处理,得到网格单元内部的流线段:

(1)对于平行单元,由于各网格顶点矢量值完全相同,单元内部矢量场无变化,此时流线在网格单元内部流向与各网格顶点矢量相同,直接计算流向所在射线与网格单元各表面的交点即可,得到的最小正数t所代表的交点就是流线流经该网格单元的出点,连接入点和出点即可得到该网格单元内部的流线段;(2)对于普通单元,通过单元矩阵特征值分解,可得到形如式(3)的矩阵表达式,然后利用牛顿迭代法求解式(3)与网格单元各表面的交点,得到的最小正数t所代表的交点就是流线流经该网格单元的出点,连接入点和出点即可得到该网格单元内部的流线段;(3)对于其他单元,按照四阶隆格-库塔进行数值积分,计算网格单元内部的流线段。虽然这种情况需要较为耗时的数值积分,但有统计数据表明,对于典型的矢量场数据,此类网格单元数目只占总网格单元数目的1%左右,并不影响流线可视化的整体效率。

2.3 普通单元流线出点的处理

对于网格单元的任一表面,分别用v1、v2和v3表示该表面的3个顶点,则流线与表面的交点计算等价于求解下述方程:

x(t)·((v1-v3)·(v2-v3))=v3·((v1-v3)×(v2-v3)).

(4)

式中,×表示向量的叉积、·表示向量的点积。

联合式(3)与式(4),利用牛顿迭代法可求出t的值。求解时,初值设为0即可。经过测试发现,对于绝大部分的求解,牛顿迭代法经过4次便可收敛,因而可以显著节省数值积分的时间,提高流线可视化的效率。对于四面体网格单元的每个表面,都可利用牛顿迭代法求出一个t值;4个t值中最小的正数t代表的交点就是流线流经该网格单元的出点。连接入点与出点,就可得到该网格单元内部的流线段。

整体算法描述如下:给定流线种子点,首先判断其在哪个网格单元内部,然后利用上述方法求解该网格单元的流线出点;此出点也是与该网格单元相邻的网格单元的流线入点,然后再利用上述方法求解出点。此过程一直进行下去,直到流线到达矢量场边界/临界点或形成封闭轨道。该算法可用伪码描述如下:

输入:流线种子点p

输出:由p生成的流线

数组E,记录形成流线的一系列点,初始化为只有一个元素p

找到p所在的网格单元cell

while(cell不为空)

switch(cell.type)//根据网格单元的不同类型分别处理

caseparallel//平行单元

v=cell.vectorAt(p)//得到p点处的矢量

t=INFINITY//将t设为无穷大

for(i=1to4)//对cell的4个表面依次处理

tmp=cell.plane[i].distanceTo(p)//得到p到各平面的距离

if(tmp

t=tmp

id=i

E.add(p+t*v)//得到出点,并加入到数组E中

break

casenormal//普通单元

t=INFINITY//将t设为无穷大

for(i=1to4)//依次求流线与4个表面的交点

tmp=Newton(p,cell)//利用牛顿迭代法求交点对应的t

if(tmp>0 &&tmp

t=tmp

id=i

E.add(getExitPoint(t))//得到出点,并加入到数组E中

break

caseother//上述两种情况之外的其他情况

p=RungeKutta-4(p,cell)//利用4阶隆格-库塔求下一积分点

while(cell.contains(p))//如果p还在cell内,则一直积分下去

p=RungeKutta-4(p,cell)

E.add(p)//将p加入到数组E中

id=findFaceID(p)//根据p找到其对应的网格单元表面

break

cell=cell.getNeighbourCell(id)//根据id找到相邻的下一个网格单元

依次连接E中的各点,得到流线并输出

当网格分辨率较低时(即单个网格单元尺寸较大),上述折线段连线形成的流线可视化效果可能不能令人满意。此时,可以利用4阶贝塞尔曲线表示网格单元内部的流线段。若用P、Q分别表示流线在此网格单元的流入点和流出点,用vP和vQ分别表示P、Q处的矢量值,用tin和tout分别表示流线进入和流出网格单元的时间,则贝塞尔曲线的4个控制点分别为:B0=P、B1=P+vP(tout-tin)/3、B2=Q-vQ(tout-tin)/3、B3=Q。

随着高性能计算机的不断发展,数值模拟的精度越来越细,网格分辨率越来越高,甚至已远高于显示屏幕的分辨率(即1个网格单元显示在屏幕上不到1个像素)。因此,在通常情况下,直接连接各网格单元的流线入点和出点形成的流线已经可以满足矢量场可视化的精度需要。

3 算法验证

在i7-3.6GHz处理器、8GB内存、Window7 64位操作系统上用C++实现了本文算法。为了验证本文方法的有效性,分别用二维矢量场数据和三维矢量场数据进行测试。第一个数据为油气田油层数据,该数据为二维数据,共有1 920 000个网格单元,生成200条流线。为测试本文中流线可视化效率,与最新的文献[8]的流线可视化时间进行对比。对于本例,文献[8]算法耗时为0.206 2 s,本文耗时为0.141 7 s,节省时间为31.28%。第二个数据是三维湍流数据,共有82 906 875个网格单元,生成1 000条流线。对于该例,文献[8]算法耗时50.68 s,本文算法耗时35.83 s,节省时间为29.30%。由以上两个测试案例可以看出,本文方法可有效提高矢量场流线可视化的效率。

4 结束语

针对大规模矢量场流线可视化效率较低的问题,本文提出一种非结构网格流线的快速可视化方法。该方法首先将流线表示成矩阵形式,从而将流线在网格单元内的积分运算转化成矩阵表示的方程与网格单元各表面求交点的问题,并利用牛顿迭代法进行求解。在实验中发现,对于该方程求解,牛顿迭代法通常4次左右便可收敛,从而可以避免繁琐的数值积分运算。实验结果表明,相比目前已有的流线可视化方法,本文方法可节省大约30%的时间。

[1] 李思昆.大规模流场科学计算可视化[M].北京:国防工业出版社,2013.

[2] NOUANESENGSY B, SHENG H W. Load-balanced parallel stre-

amline generation on large scale vector fields[J]. IEEE Tran-

saction on Visualization and Computer Graphics, 2011,17(12):85-94.

[3] SUJUDI D,HAIMISY.Integration of particle paths and streamlines in a spatially-decomposed computation[J]. Parallel Computation-

al Fluid Dynamics,1996,47(3):315-322.

[4] CHEN L,FUJISHIROI L.Optimizing parallel performance of str-

eamline visualization for large distributed flow datasets[J]. IEEE Pacific Visualization Symposium, 2008,21(4):87-94.

[5] CHEN M C, SHA D, HART J D. Fast coherent particle advection through time-varying unstructured flow datasets[J]. IEEE Transactions on Visualization and Computer Graphics, 2016,22(8):1959-1972.

[6] 彭宝云,王文珂,李思昆.大规模流场矢量线可视化的数据预取方法[J].计算机辅助设计与图形学学报,2016,28(3):464- 470.

[7] ZHANG J, GUO H,YUAN X. Efficient unsteady flow visualization with high-order access dependencies[J].IEEE Pacific Visualization Symposium (PacificVis 2016), 2016,12(2):56-60.

[8] WANG W,WANG Z K, LI S. Batch advection for the piecewise linear vector field on simplicial grids[J]. Computers & Graphics, 2016,54(2):75-83.