交叉反向学习和同粒社会学习的粒子群优化算法
2018-01-08张新明程金凤
张新明,康 强,王 霞,程金凤
(1.河南师范大学 计算机与信息工程学院,河南 新乡 453007; 2.河南省高校计算智能与数据挖掘工程技术研究中心,河南 新乡 453007)
交叉反向学习和同粒社会学习的粒子群优化算法
张新明1,2*,康 强1,王 霞1,程金凤1
(1.河南师范大学 计算机与信息工程学院,河南 新乡 453007; 2.河南省高校计算智能与数据挖掘工程技术研究中心,河南 新乡 453007)
针对社会学习粒子群优化(SLPSO)算法存在的优化效率低、收敛速度慢等问题,提出了一种改进的SLPSO算法,即基于交叉反向学习和同粒社会学习的PSO算法(CPPSO)。首先,将最优解随机纵向交叉与一般反向学习以及随机反向学习构建交叉反向学习;然后,以此交叉反向学习策略更新种群中的最优粒子位置,增强探索能力,并克服SLPSO中最优粒子无更新导致效率低下的缺点;最后,对于非最优粒子,与SLPSO采用基于维的社会学习不同,均采用新型基于粒子的社会学习机制,在提高全局搜索能力同时,更提高开采能力和搜索效率。在一组不同维基准函数上优化的实验结果表明,CPPSO的优化性能、搜索效率和普适性大幅度领先于SLPSO和其他先进的PSO改进算法,如交叉搜索PSO(CSPSO)算法、自我调节的PSO(SRPSO)算法、异构综合学习的PSO(HCLPSO)算法和反向学习和局部学习能力的PSO(RLPSO)算法。
智能优化算法;粒子群优化算法;社会学习;反向学习
0 引言
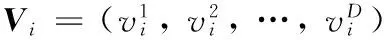
(1)
(2)
其中:c1和c2是学习因子;r1和r2是区间[0,1]中两个独立的均匀分布随机变量;d表示维的序号;t是当前迭代次数。
虽然PSO被广泛应用到诸多领域解决了许多问题,但研究发现,PSO存在早熟收敛、易陷于局部最优、种群多样性丢失等问题, 导致这些问题的原因来自PSO的更新方式。从式(1)可知,种群中的每个粒子都向着两个最优位置趋近,使得PSO快速收敛,而且采用逐个粒子动态更新最优解的方式更加剧了快速收敛;当最优粒子为局部最优点时,整个粒子群趋向局部最优,尤其在PSO解决多个局部最优值的问题时,经过一定的迭代次数之后粒子集中于局部最优值附近,导致种群多样性降低,不能跳出局部最优点。针对PSO存在的缺点,许多研究人员对PSO搜索方式进行改进以便提高其优化性能[2-5],其中不乏借助不同的学习策略来获得算法中探索能力和开采能力的平衡,提高其性能;文献[6]针对PSO的早熟收敛问题,连续使用5次变异策略,提出了一种增强领导者的PSO算法;文献[7]将PSO与两种人类最好的学习策略有机融合,提出了一种自我调节的PSO算法(Self-Regulating PSO, SRPSO);文献[8]将综合学习策略与PSO结合,提出了一种异构综合学习的PSO(Heterogeneous Comprehensive Learning PSO, HCLPSO) 算法;文献[9]通过协同反向学习与局部学习的行为,提出了一种具有反向学习和局部学习能力的PSO算法(Reverse learning and Local learning PSO, RLPSO);文献[10]将局部扰动学习和高斯子空间学习的两种学习策略与改进的骨干PSO算法融合,提出了多策略并行学习的异构PSO算法;文献[11]采用带有扰动精英的反向学习和对惯性权重的改进,提出了扰动的精英反向学习PSO算法;文献[12]将社会学习机制引入PSO算法中,得到了社会学习PSO(Social Learning PSO, SLPSO)算法, 不同于传统的PSO改进算法,SLPSO算法中的每个粒子采用向当前种群中更优粒子(称为示范者)学习的机制来更新解,提高了种群的多样性和全局搜索能力。虽然SLPSO算法提高了PSO的优化性能,但在解决高维或者复杂的优化问题时仍然存在搜索能力不足、收敛速度慢、普适性较差、搜索效率低等缺点。
针对这些问题,本文提出了一种改进的SLPSO算法,即基于交叉反向学习和同粒社会学习的PSO(Cross opposition learning and Particle-based social learning PSO, CPPSO)算法。对粒子群中的非最优粒子均采用基于粒子的社会学习新机制,在提高全局搜索能力同时,更提高局部搜索能力,加快收敛;对粒子群中的最优粒子采用交叉反向学习机制来提高全局搜索能力,二者协作共建CPPSO,以便克服SLPSO搜索效率低和收敛慢等的缺点。
1 社会学习粒子群算法
对于传统PSO及其大多数改进算法,粒子都是基于历史信息(包括整个群体发现的最优解gbest和个体发现的最优解pbest)进行更新的,而在SLPSO中,每个粒子向当前种群中的更优粒子(称为示范者)学习。每个粒子的每一维都来自不同的示范粒子,极大地提高了种群的多样性,避免了PSO存在的早熟收敛、种群多样性丢失等的缺陷。SLPSO与5个典型的改进PSO在包括平移和旋转函数的40个低维函数上和与5个最先进的大规模优化算法在7个高维函数上进行了比较。结果表明SLPSO算法在解决低维问题时表现优异,且在解决大规模问题上也很有前途。算法具体流程如下:
步骤1 初始化包含N个粒子的群体P(t),其中,N是群体大小。种群大小N和社会影响因子ε由式(3)决定。P(t)中的每个粒子保持一个随机初始化的决策向量(行为向量)Xi(t),其代表了优化问题的候选解。
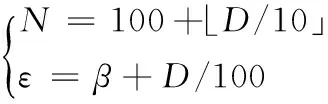
(3)
步骤2 适应度值评估。每个粒子将被分配从目标函数f(X)计算的适应度值。
步骤3 依据适应度值对粒子群由差至优排序,即排在第一的粒子适应度值是最差的,排在最后的粒子适应度值是最优的。
步骤4 社会行为学习。每个粒子(除了最优粒子外)将通过从具有更好适应度值的粒子(示范粒子)学习来矫正其行为,最优粒子不作更新。对所有非最优粒子进行行为矫正ΔXi, j(t+1),每维更新包含三个部分。第一部分:与标准PSO算法中的惯性分量相同,但惯性权重采用0~1的随机数r1。第二部分:模仿成分。取代标准PSO中的向pbest学习,粒子i向比它优秀的任何示范者学习。第三部分:社会影响成分。取代标准PSO中的向gbest学习,粒子i向当前群中所有粒子的平均行为学习,即集体行为,其中r2和r3都是0~1的随机数,k是每一维随机选择的粒子标号,j表示维的标号。
ΔXi, j(t+1)=r1·ΔXi, j(t)+r2·Ii, j(t)+r3·ε·Ci, j(t)
(4)

(5)
步骤5 当满足终止条件时,则输出最终解,算法结束;否则转到步骤2。
2 交叉反向学习和社会同粒学习的PSO
2.1 SLPSO算法存在的问题
虽然SLPSO将社会学习机制引入到PSO中,增加了全局搜索能力,提升了优化性能,但存在如下问题:
1)从整个算法流程可以看出,SLPSO每一代仅对非最优粒子进行更新,而最优粒子未参与解的更新中,从而不仅导致搜索效率低下,而且算法的搜索能力受到影响。
2)从式(4)可以看出,非最优粒子的更新采用基于维的社会学习方式,即每一维都随机选择示范粒子对应的维和整个粒子群对应维的平均值进行更新,如果需要更新D维,那就需要选择D个示范粒子用来学习,这种基于维的更新方式是从示范粒子选择一维学习,虽然能增加种群的多样性,但开采能力受到影响导致收敛速度慢,另外,一个示范粒子整体值得学习,不一定某一维就是较优的,有可能是较差的,因此这种方式不仅限制优化性能的提升,而且难以进行并行化处理。
3)虽然SLPSO更新方式不同于式(1),但式(4)与标准的PSO更新方式一样都由三项构成,且SLPSO每次更新都要计算整个种群每一维的均值,故增加了计算复杂度。
基于上述原因,SLPSO在解决复杂问题可能仍然存在搜索能力不足、收敛速度慢和搜索效率低等缺点,具有较大改进的空间。
依据现代智能优化理论,随机优化算法找到问题的最优解主要基于两种能力,即探索能力和开采能力。其中探索能力即全局搜索能力,探索整个搜索空间以寻找有前途的区域的能力;开采能力即局部搜索能力,在所识别的有前途的区域中微调搜索最优解的能力。二者互相矛盾和互相牵制,过分强调一方必定会损害另一方,只有当找到探索和开采过程之间的适当平衡时,可以获得算法的良好优化性能。因此,在基于种群的进化算法中,重要的是获得在搜索空间中的探索与开采之间的良好平衡。
本文针对SLPSO存在的问题和现代智能优化理论,提出了一种基于交叉反向学习和同粒社会学习的PSO算法(CPPSO)。首先,将基于粒子的社会学习原理运用到粒子搜索中,以整体的全维方式学习示范粒子,在提高探索能力同时,更增强开采能力,克服了SLPSO基于维的社会学习方式存在的缺点;其次,对于种群中最优个体,选择交叉反向学习机制,不仅提高种群的多样性和探索能力,而且使其探索能力与同粒社会机制的开采能力达到平衡,由此提高了搜索效率和整体的优化性能。
2.2 同粒社会学习
社会学习在社会动物的行为学习中起着重要的作用。与个人学习相反,社会学习的优点是允许个人从他人行为中学习,而不会导致个体反复实验引起的昂贵成本。为了解决SLPSO基于维的社会学习存在的问题,本文提出了新的社会学习策略,即同粒社会学习策略。所谓同粒社会学习,即从比自己较优的粒子群体中随机挑选出一个粒子,供自己学习,所有维的学习都来自同一示范粒子,这就是同粒的含义。在同粒社会学习中,每次迭代后都依据适应度值按照降序对整个粒子群进行排序,也就是说排在前面的个体一定比后面的个体优秀,是后面个体的示范者,越是后面的粒子供学习的示范粒子越多。基于同粒社会学习粒子速度与位置更新方式见式(6)和式(7):
(6)
(7)
其中:pbestk为随机选择的第k个较优粒子的个体历史最优位置,ω为惯性权重因子,c1为认知因子,i表示当前粒子的序号。这里k是从多个较优粒子中随机选取的序号,如果k等于当前粒子的序号i时,同粒社会学习的PSO就是标准PSO的认知模型,表示学习自身的过去经验;如果k等于最优粒子序号时,就是标准PSO的社会模型,表示向种群的最优者学习。与SLPSO速度更新方式的式(4)相比,式(6)只有两项,更加简洁,而且每一维的更新都来自第k个示范粒子。因为第一个粒子是最优粒子,它没有学习的示范者,故每个非最优粒子(从第2个粒子开始到最后一个粒子)从比自己优秀的粒子群里随机选择一个优者学习,提高自身的搜索能力,克服了SLPSO存在的缺点。同粒社会学习策略的伪代码见算法1。
算法1 同粒社会学习。
fori=2 toNdo
从多个示范粒子中随机选取一个示范粒子k;
每一维都执行式(6)和式(7);
end for
其中:惯性权重w=1-t/M,这里M为最大迭代次数,ω采用动态调整方式,不用人工设置,以便提高算法的可操作性。从算法1可以看出:与PSO相比,CPPSO是随机选择一个优者学习,这增加了群体的多样性和提高了探索能力。因为都整体向着较优者趋近,与SLPSO相比,更提高了开采能力,但多样性不足。
2.3 交叉反向学习
正如上文所述,基于粒子的社会学习方式增加了开采能力,但降低了种群的多样性,影响探索能力。因此为了平衡探索与开采,需进一步提高种群的多样性,也为了充分发挥每一个粒子的作用,提高效率,将交叉反向学习策略用于最优粒子的更新中。首先介绍3个概念:一般反向学习、随机反向学习和最优解随机交叉。
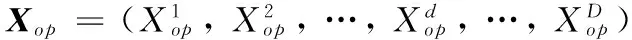
(8)
式中:ad和bd分别表示X第d维的下界和上界。

(9)
其中:ad和bd同样表示粒子的下、上边界,rand表示[0, 1]间的均匀分布随机数。

(10)
pc采用自适应线性下降的方法如式(11)所示:
pc=Cmax-(Cmax-Cmin)·t/M
(11)
其中:Cmax和Cmin分别表示最大交叉概率和最小交叉概率。为了进一步提高种群的多样性,对于全局最优个体,采用交叉反向学习机制,更有利于提高种群的多样性。即在搜索前期采用随机反向学习,在搜索后期采用自身随机交叉机制与一般反向学习的交叉,提高算法的种群多样性。在搜索后期中,具体操作方式是当随机产生的值小于等于0.5时,采用最优解随机交叉,否则采用一般反向学习。这里交叉概率采用自适应方式,即随着迭代次数的增加,交叉概率由大变小,前期交叉概率大,以便利于搜索全局最优解,后期交叉概率小,有利于提高收敛速度。交叉反向学习的伪代码见算法2。
算法2 交叉反向学习。
ift>M/2
//迭代后期
ifrand<=0.5
按照交叉概率pc产生随机维;
并执行最优解随机交叉式(10);
else
执行一般反向学习式(8);
end if
else
//迭代前期
执行随机反向学习式(9);
end if
从算法2看出,最优解随机交叉属于位置交叉,而反向学习之间以及与前者都属于时间交叉,这种空间与时间交叉的有机融合极大地保证了其探索与同粒社会学习的开采达到良好的平衡。所以最优粒子的交叉反向学习不仅是发挥其搜索作用,提高搜索效率之举,更是同粒社会学习机制所必需的。
2.4 CPPSO算法
将同粒学习策略和交叉反向学习方案有机融合,构建CPPSO算法,使得探索与开采得到良好的平衡,搜索性能得到提升。CPPSO算法主流程如图1所示。

图1 CPPSO算法主流程Fig. 1 Main flow of CPPSO
3 实验结果与分析
为了验证CPPSO算法的有效性,在一组不同维的基准函数上进行对比算法的优化实验。表1中给出了6个测试函数的信息。它们包括单峰函数如f1~f3,多峰函数如f4~f6,函数的维度选择包括低高维(30维)、中高维(100维)和高高维(200维,这种维数优化问题目前文献较少讨论),不同的维度选择可以增加寻优难度,以便验证CPPSO的普适性和处理各种复杂优化问题的能力。
3.1 对比算法与参数设置
在实验中,不仅将CPPSO测试结果与SLPSO[12]测试结果进行比较,还与其他4种最近提出的、优秀的PSO改进算法的优化结果进行对比。这些对比算法分别为CSPSO[5]、SRPSO[7]、HCLPSO[8]和RLPSO[9],在它们对应的文献中已经证明,它们的性能大幅度领先于原始PSO和其先前的改进版,具有很好的代表性和可比性。本文用5种算法对不同维度的基准函数进行优化实验,以便验证CPPSO的有效性、高优化效率和强普适性等,其共同参数设置见表2。其中,最大迭代次数M随优化函数的维数不同而不同,除SLPSO采用式(3)外,其他算法的种群大小N都为20。为公平起见,每种算法保证最大目标函数评价次数相同,并独立运行次数Num为30。另外,这些对比算法的其他参数设置与原文献相同。CPPSO需要设置的参数有两个:一个是学习因子c1,按照诸多文献推荐设置为1.494 45; 另一个是交叉概率,采用自适应方式,其中,Cmax取最大值,即Cmax=1,而对于Cmin的取值,通过大量的实验验证,Cmin=0.3为最佳,受版面所限,对Cmin取值不作讨论。仿真实验的环境:操作系统为Windows 7,PC机为主频为3.10 GHz的CPU和4 GB内存,编程语言为Matlab R2014a。

表1 Benchmark函数信息表Tab. 1 Functions of Benchmark
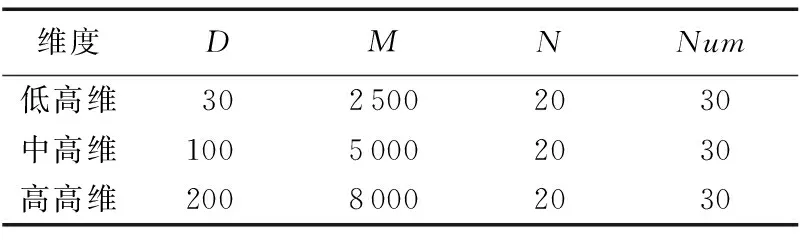
表2 基本参数设置Tab. 2 Parameters setting
3.2 优化性能比较
3.2.1 与SLPSO、CSPSO、SRPSO和HCLPSO算法的比较
在6个基准函数上对不同维度(30维、100维和200维)的测试结果见表3~6,其中包含30次独立运行的寻优结果的最大值Vmax、最小值Vmin、均值Mean、标准差值Std,下划线表示测试结果的最优者。其中均值和标准差值越小说明该算法的搜索能力越好和稳定性越强。
表3给出了5种算法在30维函数上的测试结果。从表中可以看出,在各种对比数据上,CPPSO拥有极大的优势,大幅度领先于对比算法。在f3和f5上,CPPSO的均值达到了理想最优值0,即表1的Fmin,CSPSO只有在f5上的均值达到了理想最优值0,SLPSO及另外2种对比算法没有均值达到理想最优值。而对于函数f1、f2、f4、f6,CPPSO虽然没有达到其理想的最优值,但与包含SLPSO的4种对比算法相比,CPPSO无论在Vmax、Vmin、Mean和Std上都远远优于4个对比算法。除此之外,5种算法中在Vmin上有3种算法都得到了最优值,分别是CPPSO、SLPSO、CSPSO。从30维函数上的运行结果上可知,CPPSO在低高维函数上的优化性能表现最优。

表3 5种算法在30维函数上的测试结果Tab. 3 Results of 5 algorithms on 30-dimensional functions
表4给出了5种算法在100维函数上的测试结果。从整体来看,CPPSO算法,沿袭了30维函数上的高性能态势,仍然是5种算法中的最优者,其优化性能远优胜于4种对比算法。在f3和f5上,CPPSO的Mean再次达到了理想最优值0。对于函数f1、f2、f4和f6,CPPSO算法虽然没有达到理想最优值,但与4种对比算法相比,CPPSO算法的优化性能仍然最优的。相比30维函数,100维函数的维数增加了,优化复杂度增加了,但从实验结果看,CPPSO在中高维基准函数上的优化性能并没有明显地减退。而对比算法随着维数的增加,优化性能明显下降了,如在30维f2上SLPSO和CSPSO的均值分别为2.939 1E-52和1.364 2E-50,在100维f2上分别为5.954 0E-47和3.823 0E-29,结果精度下降了许多。

表4 5种算法在100维函数上的测试结果Tab. 4 Results of 5 algorithms on 100-dimensional functions
表5列出了5种算法在200维函数上的测试结果。10~100维函数的优化问题是目前国内外文献主要讨论的问题,200维函数的优化问题,目前国内外相关研究相对较少,主要原因是随着维数增加,优化难度加大,一般智能优化算法难以在如此高维的函数上获得理想的优化结果。从表5可以看出,CPPSO仍然获得了最优性能。在f3和f5上,CPPSO仍然达到了理想的最优值0。在其他基准函数上,仍然大幅度优于对比算法。与30维和100维相比,CPPSO在200维函数上的优化性能有所下降,但与对比算法相比,下降的趋势较为缓慢。200维函数上的测试结果足以表明CPPSO能够很好地处理高高维函数的优化问题。
以上在不同维度基准函数上的实验结果证明了CPPSO的可行性,不仅在不同维度单峰函数上有较好的收敛精度,而且在不同维度多峰函数上显示了更好的全局搜索能力,以明显的优势优于对比算法。
总之,不管是低高维乃至高高维函数,CPPSO都显示出极好的优化性能,具有较强的普适性。这是由于新型的社会学习使得非最优粒子向着自己的较优粒子学习,具有较好开采能力的结果,而且还是由于最优粒子采用交叉反向学习机制使得粒子探索能力增强,与同粒社会学习的开采能力获得良好平衡的结果。

表5 5种算法在200维函数上的测试结果Tab. 5 Results of 5 algorithms on 200-dimensional functions
3.2.2 与RLPSO算法的比较
为了进一步说明CPPSO算法的寻优性能,将CPPSO算法与目前国内最优秀的RLPSO算法[9]进行性能对比。这两种算法都采用了反向学习机制,具有较强的可比性。两种算法在6个函数上维数均为30,种群大小为20。其实验结果见表6, 其中RLPSO的实验数据直接来自对应的文献[9]。
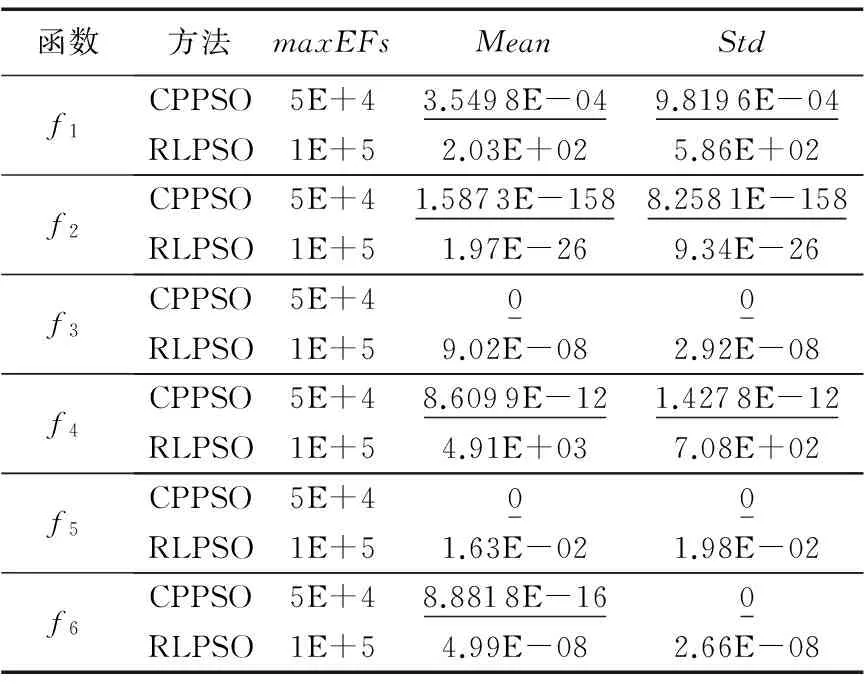
表6 CPPSO与RLPSO算法的优化结果对比Tab. 6 Results comparison between CPPSO and RLPSO
表6中, 对于单峰函数f1~f3,CPPSO算法在f3上的均值达到了理想的最优值0,在f1和f2上,CPPSO的均值也比RLPSO小得多,说明其局部搜索能力强,收敛精度较高,具有极强的稳定性。在优化多峰函数f4~f6时,不管是均值还是标准差值,CPPSO大幅度优于RLPSO,说明其全局寻优能力强。总之,相比RLPSO,CPPSO优化性能更好,收敛速度更快以及收敛精度更高,而且对比实验中本文提出CPPSO的最大目标函数评价次数(maxEFs)比RLPSO少许多,前者为5E+4,后者为1E+5,进一步说明CPPSO比RLPSO优化性能好。虽然二者都使用了反向学习策略,但二者性能差距巨大,其原因是CPPSO能将随机反向学习、一般反向学习和最优解随机纵向交叉有机融合,并一直用来更新最优解,很好地与同维社会学习策略配合,使得算法的探索与开采达到较好的平衡,因此整体性能得到大幅度提升。
3.2.3 运行时间比较与计算复杂度分析
为了考察CPPSO的优化速度,统计5种算法运行时间。表7给出了在所有基准函数上独立运行30次的平均时间。
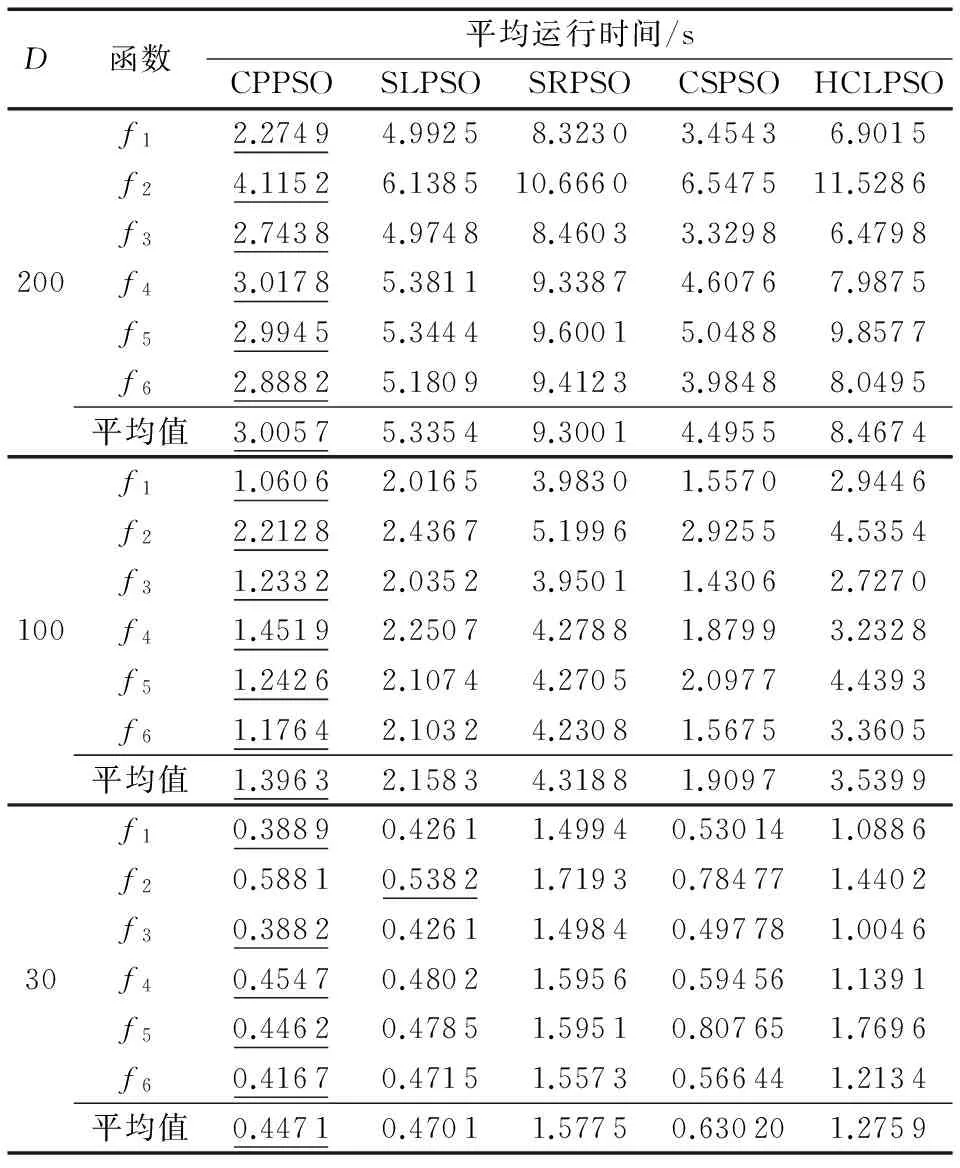
表7 5种算法在高维函数上的平均运行时间Tab. 7 Average runtime of 5 algorithms on high-dimension functions
从表7中可以看出,不管从每个基准函数的单向运行时间,还是从所有基准函数的平均运行时间,除了在30维f2外,CPPSO的耗时是5种算法中最少的。
一个优化算法的复杂度由两部分组成,即目标函数评价次数和算法自身的复杂度,对于前者,5种算法相同,即它们有相同的目标函数评价次数,所以5种算法的运行耗时的差别主要源于算法自身复杂度的不同。CPPSO作为SLPSO的改进算法,其运行耗时更少,主要原因有二:第一、CPPSO采用基于维的并行方式进行搜索节省了时间,在30维上,这种并行方式在运行耗时上的优势不明显,CPPSO的平均耗时为0.447 1 s,比SLPSO的运行时间(0.470 1 s)稍少,然而随着问题维数增加,这种优势逐渐显著,虽然2种算法在处理维度更高的基准函数时的运行耗时都有所增加,但CPPSO平均耗时较SLPSO平均耗时的差距明显增大;其二、CPPSO中新的社会学习策略中的速度更新公式计算复杂度低于SLPSO中式(4)的计算复杂度,从而减少了运行耗时。总的来说,CPPSO在100维基准函数上的耗时为1.396 3 s,大约分别是SLPSO、SRPSO、CSPSO和HCLPSO的64.69%、32.33%、73.12%和39.44%。在200维基准函数上的耗时CPPSO为 3.005 7 s,大约分别是SLPSO、SRPSO、CSPSO和HCLPSO的56.33%、32.32%、66.86%和35.50%。 由此可知,CPPSO用最少的时间使优化性能最大化,故有更高的优化效率。
3.2.4 显著性分析
为了验证实验所得结果的有效性,对CPPSO在100维函数上获得的结果与其他对比算法的结果进行了t-检验(双尾)及显著性分析。置信水平α=0.05,检验结果如表8所示,其中,在结果一栏分别用“+”“=”及“-”表示;p<0.05有明显显著差异,0.05
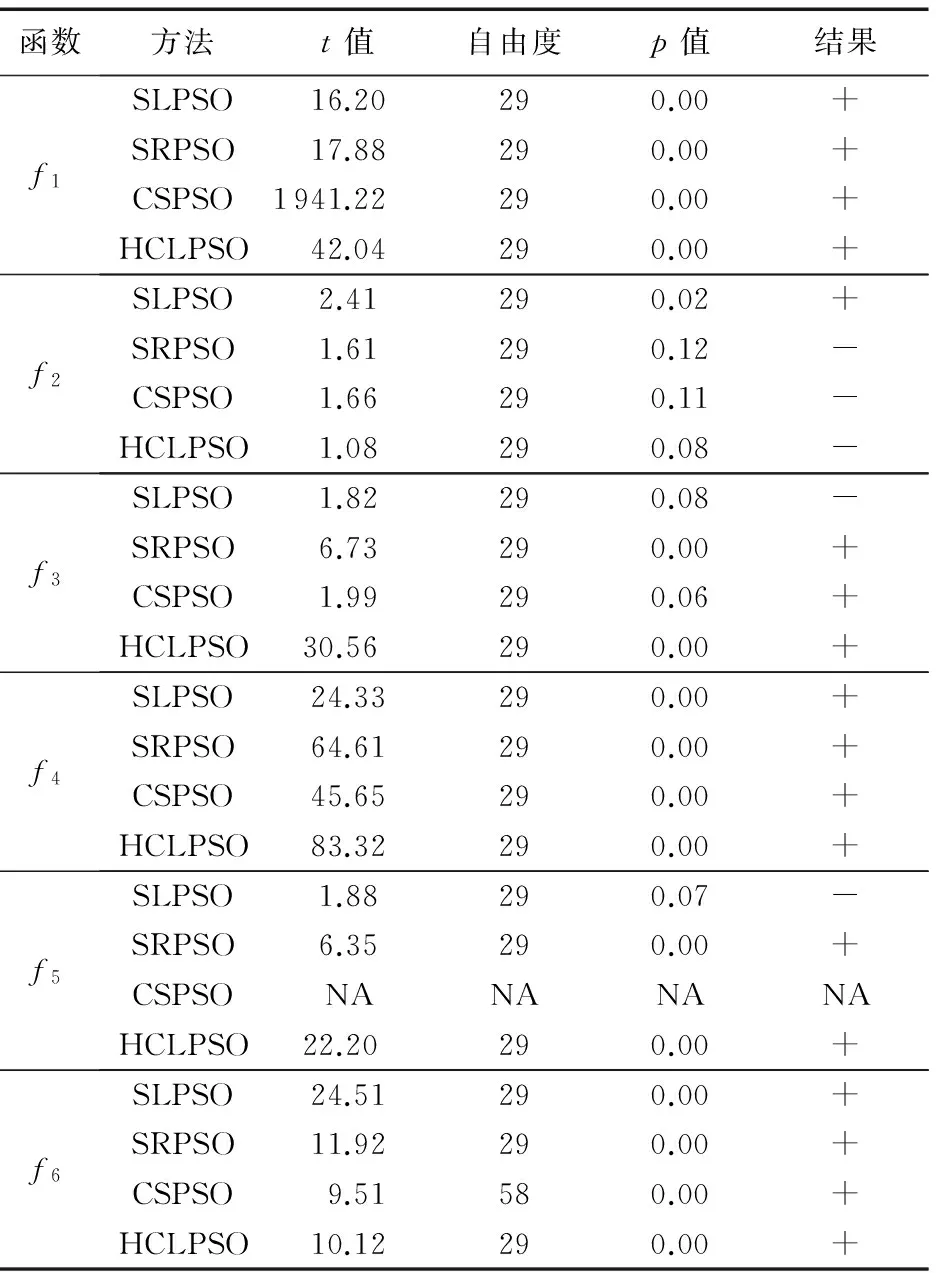
表8 CPPSO与对比算法的t-检验结果Tab. 8 t-test results of CPPSO with the other comparison algorithms
从表8可以看出,对于t-检验得到的23个结果中,CPPSO算法有18次较对比算法显著更优,且均有显著差异,有5次无显著差异,没有较其他对比算法显著更劣的情况,从而验证了CPPSO算法优秀的性能。
4 结语
针对SLPSO算法存在的收敛速度慢、普适性弱等缺点,本文提出了一种改进的SLPSO算法,即基于交叉反向学习和同粒社会学习的PSO算法(CPPSO)。首先,将基于粒子的社会学习原理运用到粒子搜索中,以整体的全维方式学习示范粒子,提高局部搜索能力和收敛速度,避免了SLPSO基于维的社会学习方式存在的缺点;其次,对于种群中最优个体,选择交叉反向学习机制,不仅提高自身的搜索能力和提高种群的多样性,而且平衡了探索与开采能力,由此提高了搜索效率和整体的优化性能。该算法的普适性强,在不同维度的基准函数优化上效果比目前最优秀的PSO改进算法更好,优化性能大幅度领先于目前同类算法,在大规模和复杂优化问题上具有较大的应用前景。
References)
[1] 张新明, 涂强, 尹欣欣, 等. 嵌入趋化算子的PSO算法及其在多阈值分割中的应用 [J]. 计算机科学, 2016, 43(2): 311-315. (ZHANG X M, TU Q, YIN X X, et al. Chemotaxis operator embedded particle swarm optimization algorithm and its application to multilevel thresholding[J]. Computer Science, 2016, 43(2): 311-315.)
[2] LIU H, XU G, DING G, et al. Integrating opposition-based learning into the evolution equation of bare-bones particle swarm optimization[J]. Soft Computing, 2014, 19(10): 539-546.
[3] SHANG J, SUN Y, LI S, et al. An improved opposition-based learning particle swarm optimization for the detection of SNP-SNP interactions[J]. Biomed Research International, 2015, 2015: 524821.
[4] DONG W, KANG L, ZHANG W. Opposition-based particle swarm optimization with adaptive mutation strategy[J]. Soft Computing, 2017,21(17): 5081-5090.
[5] MENG A B, LI Z, YIN H, et al. Accelerating particle swarm optimization using crisscross [J]. Information Sciences, 2016, 329(S1): 52-72.
[6] JORDEHI A R. Enhanced Leader PSO (ELPSO): a new PSO variant for solving global optimization problems[J]. Applied Soft Computing, 2015, 26(1): 401-417.
[7] TANWEER M R, SURESH S, SUNDARARAJAN N. Self regulating particle swarm optimization algorithm[J]. Information Science, 2015, 294: 182-202.
[8] LYNN N, SUGANTHAN P N. Heterogeneous comprehensive learning particle swarm optimization with enhanced exploration and exploitation[J]. Swarm & Evolutionary Computation, 2015, 24: 11-24.
[9] 夏学文, 刘经南, 高柯夫, 等. 具备反向学习和局部学习能力的粒子群算法[J]. 计算机学报, 2015, 38(7): 1397-1407. (XIA X W, LIU J N, GAO K F, et al. Particle swarm optimization algorithm with reverse-learning and local-learning behavior[J]. Chinese Journal of Computers, 2015, 38(7): 1397-1407.)
[10] 王芸, 孙辉. 多策略并行学习的异构粒子群优化算法[J]. 计算机应用, 2015, 35(11): 3238-3242.(WANG Y, SUN H. Heterogenous particle swarm optimization algorithm with multi-strategy parallel learning [J]. Journal of Computer Applications, 2015, 35(11): 3238-3242.)[11] 李俊, 汪冲, 李波,等. 基于扰动的精英反向学习粒子群优化算法[J]. 计算机应用研究, 2016, 33(9): 2584-2591.(LI J, WANG C, LI B, et al. Elite opposition-based particle swarm optimization based on disturbances [J]. Application Research of Computers, 2016, 33(9): 2584-2591.)
[12] CHENG R, JIN Y C. A social learning particle swarm optimization algorithm for scalable optimization[J]. Information Sciences, 2015, 291(6): 43-60.
This work is partially supported by Key Scientific and Technologies Project of Henan Province (132102110209), the Research Program of Basic and Advanced Technology of Henan Province (142300410295).
ZHANGXinming, born in 1963, M. S., professor. His research interests include intelligent optimization algorithm, digital image processing, pattern recognition.
KANGQiang, born in 1989, M. S. candidate. His research interests include intelligent optimization algorithm, digital image processing.
WANGXia, born in 1993, M. S. candidate. Her research interests include intelligent optimization algorithm, digital image processing.
CHENGJinfeng, born in 1990, M. S. candidate. Her research interests include digital image processing.
Particleswarmoptimizationalgorithmwithcrossoppositionlearningandparticle-basedsociallearning
ZHANG Xinming1,2*, KANG Qiang1, WANG Xia1, CHENG Jinfeng1
(1.CollegeofComputerandInformationEngineering,HenanNormalUniversity,XinxiangHenan453007,China;2.EngineeringTechnologyResearchCenterforComputingIntelligence&DataMiningofHenanProvince,XinxiangHenan453007,China)
In order to solve the problems of the Social Learning Particle Swarm Optimization (SLPSO) algorithm, such as slow convergence speed and low search efficiency, a Cross opposition learning and Particle-based social learning Particle Swarm Optimization (CPPSO) algorithm was proposed. Firstly, a cross opposition learning mechanism was formulated based on combining general opposition learning, random opposition learning and vertical random cross on the optimal solution. Secondly, the cross opposition learning was adopted for the optimal particle to improve the population diversity, exploration ability and avoid the disadvantage of SLPSO’s slow convergence and low search efficiency. Finally, a novel social learning mechanism was adopted for the non-optimal particles in the particle swarm, and the new social learning method used particle-based approach, instead of the dimension-based one of SLPSO, not only improved the exploration capacity, but also improved exploitation and the optimization efficiency. The simulation results on a set of benchmark functions with different dimensions show that the optimization performance, search efficiency and generalizability of the CPPSO algorithm are much better than those of the SLPSO and the advanced PSO algorithms such as Crisscross Search PSO (CSPSO), Self-Regulating PSO (SRPSO), Heterogeneous Comprehensive Learning PSO (HCLPSO) and Reverse learning and Local learning PSO (RLPSO).
intelligent optimization algorithm; Particle Swarm Optimization (PSO) algorithm; social learning; opposition learning
2017- 05- 11;
2017- 05- 24。
河南省重点科技攻关项目(132102110209);河南省基础与前沿技术研究计划项目(142300410295)。
张新明(1963—),男,湖北孝感人,教授,硕士,CCF会员,主要研究方向:智能优化算法、数字图像处理、模式识别; 康强(1989—),男,河南郑州人,硕士研究生,主要研究方向:智能优化算法、数字图像处理; 王霞(1993—),河南新乡人,硕士研究生,主要研究方向:智能优化算法、数字图像处理; 程金凤(1990—),女,河南夏邑人,硕士研究生,主要研究方向:数字图像处理。
时间 2017- 08- 17 09:04:21。 网络出版地址 http://kns.cnki.net/kcms/detail/51.1307.TP.20170817.0904.002.html。
1001- 9081(2017)11- 3194- 07
10.11772/j.issn.1001- 9081.2017.11.3194
(*通信作者电子邮箱xinmingzhang@126.com)
TP181
A
