非差观测模型的BDS静态精密单点定位算法

杨 虎，徐爱功，祝会忠，马天明

(辽宁工程技术大学 测绘与地理科学学院，辽宁 阜新 123000)

非差观测模型的BDS静态精密单点定位算法

杨 虎，徐爱功，祝会忠，马天明

(辽宁工程技术大学 测绘与地理科学学院，辽宁 阜新 123000)

为了进一步缩短BDS静态精密单点定位的收敛时间、提高定位精度，研究BDS精密单点定位的数学模型、各项误差改正和估计方法，采用非差观测模型、消电离层组合对非差参数进行估计，改正对流层延迟、相位偏差等各项误差，并对BDS系统下的可视卫星数、PDOP值、收敛时间及定位精度进行分析。实验结果表明：BDS静态精密单点定位水平方向的精度优于2 cm，高程方向优于5 cm；与GPS精密单点定位类似，E方向上定位精度较N方向稍差。

BDS；精密单点定位；收敛时间；定位精度

0 引言

精密单点定位(precise point positioning，PPP)利用国际全球卫星导航系统服务组织(International GNSS Service，IGS)提供的精密卫星轨道和钟差，处理单台接收机的非差伪距和载波相位观测值，估计测站3维坐标、接收机钟差和对流层延迟等参数，同时利用精细的改正模型改正定位过程中出现的各种误差，以确定单台接收机在国际地球参考框架(international terrestrial reference frame，ITRF)坐标系下的坐标，在全球范围内可实现高精度的定位与测时[1]。精密单点定位(precise point positioning，PPP)突破了相对定位中的距离限制，利用单台全球卫星导航系统(global navigation satellite system，GNSS)接收机在全球范围内进行静态或动态作业，可直接获得在ITRF框架下dm级至cm级的实时动态导航定位结果和mm级的静态定位结果，已广泛应用于测绘、航空、气象、科学考察和卫星定轨等诸多领域。

北斗卫星导航系统(BeiDou navigation satellite system，BDS)是中国正在实施的自主发展、独立运行的全球卫星导航系统[2]。截至2012-12-28，BDS已有5颗地球静止轨道(geostationary Earth orbit，GEO)、5颗倾斜地球同步轨道(inclined geo-synchronous orbits，IGSO)和4颗中圆地球轨道(medium Earth orbit，MEO)卫星在轨运行，初步形成了亚太地区的导航定位服务能力。随着BDS的逐步完善和发展，基于BDS的PPP技术吸引了国内外学者的广泛关注。文献[3]采用实测数据和我国自主研制的精密数据处理软件PANDA，实现了BDS静态PPP，定位结果精度达到cm级。文献[4]利用北京站和武汉站一个星期的观测数据进行了BDS的静态试验，得到了精度1～2 cm的BDS静态解。文献[5]也取得了BDS静态PPP水平方向1～2 cm、垂直方向3～4 cm的定位精度。

本文提出基于非差的BDS多频PPP算法，采用非差观测模型、消电离层组合，对对流层延迟、相位偏差等各项误差进行模型改正和参数估计，计算BDS静态PPP定位结果，最后进行精度分析与评价。

1 BDS PPP数学模型

1.1 多频PPP观测方程

与全球定位系统(global positioning system，GPS)PPP类似，BDS PPP的基本观测方程采用多频无电离层组合以消除电离层一阶项误差的影响。BDS具有B1、B2、B3共3个信号频率，采用B1、B2频率上的相位和伪距观测值进行无电离层组合，其具体观测方程[6]为：

(1)

(2)

1.2 误差改正策略

通过无电离层组合消除电离层延迟一阶项的影响后，PPP的待估参数包括测站坐标、接收机钟差、天顶对流层延迟，以及各卫星连续观测弧段内的模糊度参数[7]。采用非差处理模式，数据预处理采用单站数据预处理方法，尽可能地探测与修复周跳并采用参数消去法剔除异常值[8]；对未修复的周跳引入新的模糊度参数，对未探测的周跳与粗差观测值，在估计模块的质量控制中进行处理；考虑尽可能多的改正项，对未能精确模型化的误差因素，通过参数估计吸收；参数估计模块采用最小二乘估计器，逐个历元建立观测方程[9]。具体的参数估计策略如表1所示。

表1 参数估计及其策略

2 BDS PPP误差改正模型

PPP的误差改正模型包括与卫星有关的误差、与传播路径有关的误差和与接收机有关的误差[10]。针对表1列出的误差参数，介绍主要的PPP误差改正项。

2.1 天线相位缠绕

天线相位缠绕是指卫星或接收机天线绕竖轴旋转时，引起的载波相位观测值发生变化的现象。GNSS右旋极化方式的卫星信号使得载波相位观测值与卫星和接收机天线的朝向有关。

在静态模式下，接收机天线不发生旋转，不存在天线相位缠绕的影响；但是对于GNSS PPP，无法有效消除卫星天线相位缠绕的影响，其误差可达到dm级：因此必须对其进行改正。相位缠绕改正公式可表示为

Δφ=2Nπ+Δφ。

(3)

式中：

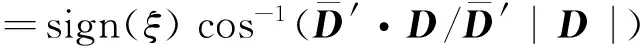
(4)

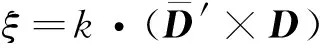
(5)

D=x-k(k·x)+k×y；

(6)

(7)

N=nint[(Δφprev-Δφ)/2π]。

(8)

2.2 固体潮汐

地球固体潮是指在摄动天体(太阳和月球)的万有引力作用下，使固体地球表面产生周期性的涨落而发生形变的现象。使用长时间观测的方法仅可以消除大部分周期项的影响，长期项和残余的周期项影响仍然存在，在径向方向可达12 cm，水平方向可达5 cm。对于单测站的PPP来说，由于是直接求解测站坐标，若要获得高精度的定位结果，必须利用模型对固体潮进行改正。固体潮对测站位置影响的近似公式可表示为

(9)

式中：rE为地球半径；Xj和Xp分别表示摄动天体(太阳、月球)和测站在地心参考框架中的坐标向量；G为地球引力参数；ME为地球总质量；GMj为摄动天体(j=1表示月球，j=2表示太阳)的引力参数；h2、l2为Love和Shida数(h2=0.609，l2=0.0852)；φ、λ分别为测站的纬度和经度(东为正)；θ为格林尼治平恒星日。

2.3 相对论效应

相对论效应是指由于接收机和卫星钟所处的状态不同而引起2台钟之间产生相对钟误差的现象。GNSS接收机钟比卫星钟走得慢，每秒相差0.45 ms左右。为了消除相对论相应的影响，在GNSS卫星发射之前，将其钟的标准频率减小约0.004 5 MHz；但是由于受卫星轨道高度变化、地球自转运动和地球重力场变化等影响，相对论效应改正数并非常数。经过上述改正后，使用精密星历进行PPP解算时，其残余误差引起的测距误差可表示为

(10)

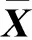
2.4 地球自转

GNSS定位采用的是与地球一起转动的协议地球坐标系，若某一时刻卫星从该瞬时空间位置向地面发射信号，当卫星信号到达地面接收机时，与地球固连的协议地球坐标系相对于卫星信号发射瞬间的位置已产生了旋转(绕Z轴旋转)。此时，计算卫星位置时必须考虑到地球旋转改正，若取ω为地球的自传角速度，则旋转的角度为

(11)

(12)

式中(Xj，Yj，Zj)为卫星瞬时坐标。

2.5 对流层延迟

对流层是无线电波传播的随机不均匀介质，电磁波通过对流层时由于传播速度的变化以及传播路径弯曲而产生延迟。对流层延迟分为干延迟和湿延迟。文献[10]指出对流层延迟的大小对收敛速度的影响非常明显，因此对流层延迟的改正是必不可少的。

将根据大量的长期观测得到的气象资料用解析的方法，以地表的气象参数近似反演天顶方向上的气象时空变化，建立中性大气天顶延迟模型，并建立相应的投影函数，将传播路径上的对流层延迟映射到天顶方向，便于对流层延迟的参数化。

对于对流层干延迟，采用Saastamoinen模型进行改正，其公式为

(13)

式中：Ps为地面气压(mbar)；Ts为地面温度(℃)；es为地面水气压(mbar)；rh为相对湿度；f(φ，h)为地球自转所引起重力加速度变化的修正，φ为测站的地心纬度(°)，h为测站高程(km)；ΔDz，trop为天顶总对流层延迟；ΔDz，dry、ΔDz，wet分别为天顶对流层干延迟与湿延迟。

一般情况下，对流层延迟的干分量几乎能得到完全改正。而对于湿分量，由于大气层中水汽分布在时间和空间上变化的随机和复杂性，利用地面气象资料很难模拟上层空间的水汽变化；模型改正后的对流层延迟残余影响还是在cm量级，这部分残差一般利用一阶高斯-马尔可夫或随机游走过程进行估计[2]。GMF投影函数由于篇幅限制，不作详细介绍，可参看文献[2]。

随机游走模型是非平稳的随机过程，随机游走过程的方差随时间而变化。随机游走过程的计算方法为

(14)

其离散化方程为

(15)

式中：ρ(t)为t时刻随机游走模型的方差；w(t)为方差的零均值白噪声；Δt为时间间隔。

2.6 天线相位偏差

天线相位偏差包含两方面的内容：一方面是由天线平均相位中心与天线几何中心不一致所产生的平均相位中心偏差(phase center offset，PCO)；另一方面是由观测时刻的瞬时天线相位中心与平均相位中心不一致所产生的天线平均相位中心变化(phase center variations，PCV)。天线相位中心偏差随着卫星信号输入的强度与方向而变化，其值可达数mm到数cm。

由于目前IGS只提供了粗略的BDS卫星端PCO改正，尚无机构或组织提供BDS卫星端PCV以及接收机端的PCO与PCV信息；因此无法进行精确的天线相位中心偏差及其变化改正[7]。

3 实验与结果分析

为了评定BDS PPP的定位性能，选取了8个测站2016年DOY101—107共7 d的BDS双系统的GNSS观测数据进行静态PPP试验。试验数据来源于IGS的MGEX(muti-GNSS experiment)观测网，所选测站信息如表2所示。CMUM、CPNM、EUSM均分布在亚洲南部，CUT0站位于澳大利亚的Curtin大学内，DAE2、GMSD分别位于韩国与日本，HARB站位于南非，NRMG位于大洋洲中部。

观测数据采样间隔为30 s，截至高度角7°，精密产品采用IGS提供的BDS 30 s精密星历和30 s钟差产品。为比较分析，对各测站同时进行GPS PPP解算，并与该站准确值进行对比。

实验解算各测站24 h的观测数据，将解算结果与准确值做差，获得E、N、U共3个方向上的坐标偏差以分析BDS PPP的收敛时间和定位精度。

表2 测站相关信息

3.1 收敛速度分析

收敛的判断依据定义为E、N、U各向定位偏差均优于1 dm。为确保结果的可靠性，同时检查了首次收敛时刻后20个历元的位置偏差，只有当连续20个历元的偏差都在限值以内，才认为当前历元的定位结果收敛。

以DOY101 CUT0站单天的定位结果为例，比较分析了BDS/GPS PPP的定位偏差序列，如图1所示。

从图1中可以看出，BDS静态PPP经过50 min可以收敛，而GPS静态PPP收敛时间相对较短，约30 min。

图2为该时段BDS、GPS PPP的位置精度衰减因子(position dilution of precision，PDOP)值和可视卫星数。

从图中可以看出：尽管大部分时间BDS卫星数多于GPS，但由于目前BDS的MEO卫星数较少，总体图形结构变化不如GPS星座显著；而且由于当前BDS的跟踪站数量有限，BDS的精密轨道精度较低，导致BDS PPP的收敛时间长于GPS。

对各天数据的静态PPP收敛时间进行统计，得到各天的平均收敛时间，结果如图3所示。

从图3中可以看出：对基于BDS、GPS系统的PPP定位，各天之间的平均收敛具有良好的一致性，天与天之间并无明显差异；BDS平均收敛时间均在60 min以上，而GPS平均收敛时间均小于40 min。所有数据的收敛时间统计如下：BDS静态PPP的平均收敛时间为77.7 min；GPS静态PPP的平均收敛时间为32.6 min。

图1 DOY101 CUT0站单天BDS、GPS静态PPP定位偏差序列

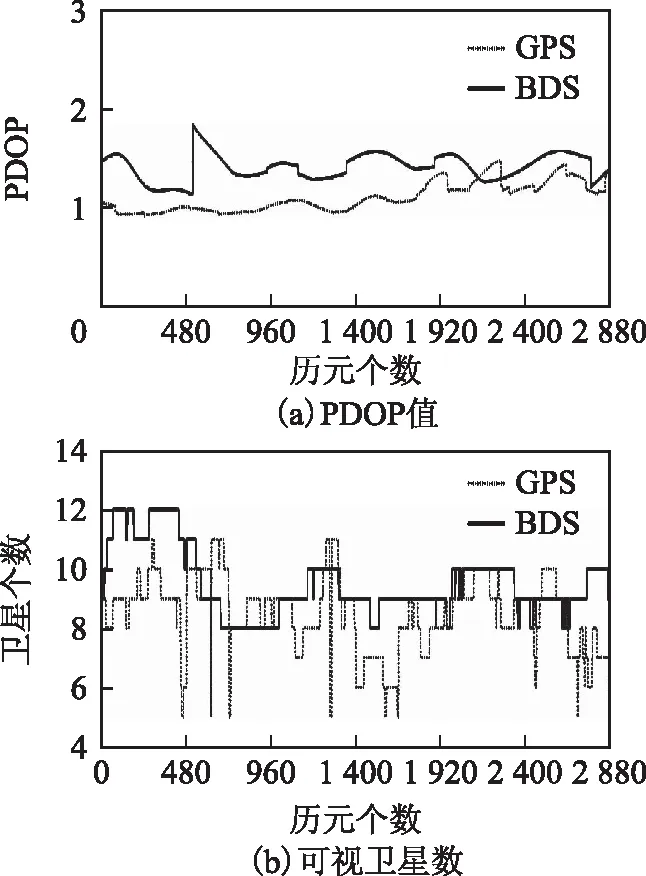
图2 DOY101 CUT0站单天BDS、GPSPDOP值和卫星数

图3 DOY101-107各天静态PPP平均收敛时间

众所周知，PPP的定位结果受卫星轨道和钟差产品精度、星座几何强度的影响较为明显。目前，BDS的精密卫星产品的精度较GPS差，且无法精确改正PCO和PCV误差[7]；而且，BDS的可用卫星数只有23颗，而GPS有31颗，其几何强度远比BDS好：因此，当前条件下BDS PPP的收敛时间明显长于GPS PPP。

3.2 BDS/GPS定位精度分析

为了定量分析收敛后BDS PPP的定位精度及稳定性，对每天的解算结果进行统计，计算其定位偏差的均方根(root mean square，RMS)。以DOY101为例，表3中给出了各测站单天解的RMS值。

表3 各站单天解E、N、U方向上的RMS值 cm

从表中可以看出，BDS静态PPP单天解水平方向精度优于2 cm，高程方向优于5 cm；GPS静态PPP水平与高程方向精度分别优于1 cm、2 cm。整体而言，BDS PPP收敛后的定位精度要略低于GPS PPP；这主要是由于当前BDS的MEO卫星数较少，卫星分布及定位的几何图形结构比GPS差，且轨道和钟差产品精度相对较低而导致的。从图中可明显看出，2种PPPN方向定位精度均优于E方向，这是由于PPP保留浮点解，未将模糊度参数固定为整数的缘故[9]。

4 结束语

本文利用IGS发布的BDS精密星历和钟差文件，编程实现了BDS 静态PPP算法，采用IGS站提供的8个测站7 d的数据进行实验，并以准确值作为参考进行对比。结果表明：1)BDS静态PPP由于可视卫星数、地面跟踪站数量较少以及精密产品精度较低的影响，收敛时间长于GPS 静态PPP，约为80 min；2)BDS静态PPP单天解定位精度水平方向优于2 cm，高程方向优于5 cm，相比于GPS静态PPP水平1 cm、高程2 cm的精度相差不多，可以认为目前BDS在区域的PPP性能与GPS相当。随着BDS星座的扩建、地面跟踪站的增多，以及精密产品精度的提高，其收敛时间和定位精度将得到进一步提高。

[1] 周承松，彭月，张小红，等.精密单点定位收敛时间的确定方法研究[J].导航定位学报，2016，4(1)：80-87.

[2] 徐宗秋.基于多导航卫星系统的精密单点定位模型与方法研究[D].阜新：辽宁工程技术大学，2013.

[3] 施闯，赵齐乐，李敏，等.北斗卫星导航系统的精密定轨与定位研究[J].中国科学：地球科学，2012，42(6)：854-861.

[4] 马瑞，施闯.基于北斗卫星导航系统的精密单点定位研究[J].导航定位学报，2013，1(2)：7-10.

[5] 王阅兵，游新兆，金红林，等.北斗导航系统与GPS精密单点定位精度的对比分析[J].大地测量与地球动力学，2014，34(4)：110-115.

[6] 鲍建宽，陈伟荣，高成发.精密单点定位的数学模型选择[J].黑龙江工程学院学报(自然科学版)，2013，27(2)：1-4，7.

[7] 张小红，左翔，李盼，等.BDS/GPS精密单点定位收敛时间与定位精度比较[J].测绘学报，2015，44(3)：250-255.

[8] 张宝成，欧吉坤，袁运斌，等.基于GPS多频原始观测值的精密单点定位算法及应用[J].测绘学报，2010，39(5)：478-483.

[9] 涂锐，黄观文，凌晴.GPS单频精密单点定位的研究发现[J].测绘科学，2011，36(3)：68-70.

[10] 曹相，高成发.GPS精密单点定位(静态)影响收敛速度的因素分析[J].现代测绘，2007，30(1)：19-21.

BDSstaticprecisepointpositioningalgorithmbasedonnon-differenceobservationmodel

YANGHu，XUAigong，ZHUHuizhong，MATianming

(School of Geomantics，Liaoning Technical University，Fuxin，Liaoning 123000，China)

In order to improve the the convergence time and positioning accuracy of BDS static precision point positioning，the paper studied on the mathematical models of BDS precise point positioning and the methods of error correction and estimation，used tnon-difference observation model，ionosphere combination to estimate the non-difference parameters and correct the errors of troposphere delay，phase deviation and so on.Then the visible satellites，PDOP values，convergence time and positioning accuracy of BDS system were analyzed.Experimental result showed that the accuracy of horizontal direction of BDS static precision point positioning could be better than 2 cm，and that of elevation direction could be better than 5 cm；moreover，similar with GPS precision point positioning，the accuracy of BDS static precision point positioning in the east would be worse than that in the north.

BDS；precision point positioning；convergence time；positioning accuracy

2016-12-12

国家重点研发计划项目(2016YFC0803102)；辽宁省高等学校创新团队项目(LT2015013)。

杨虎(1992—)，男，安徽阜阳人，硕士研究生，研究方向为GNSS高精度定位。

杨虎，徐爱功，祝会忠，等.非差观测模型的BDS静态精密单点定位算法[J].导航定位学报，2017，5(4)：86-91.(YANG Hu，XU Aigong，ZHU Huizhong，et al.BDS static precise point positioning algorithm based on non-difference observation model[J].Journal of Navigation and Positioning，2017，5(4)：86-91.)

10.16547/j.cnki.10-1096.20170416.

P228

A

2095-4999(2017)04-0086-06