基于迭代凸优化的导弹探测时间估算方法
2018-01-08葛瑞星周青松张剑云谌诗娃
葛瑞星,周青松,张剑云,谌诗娃
(国防科学技术大学 电子对抗学院,安徽 合肥 230037)
基于迭代凸优化的导弹探测时间估算方法
葛瑞星,周青松,张剑云,谌诗娃
(国防科学技术大学 电子对抗学院,安徽 合肥 230037)
为准确估算远程预警雷达对弹道导弹探测的时间窗口,需要联立导弹轨迹与雷达探测范围的数学模型,求解非线性二次方程组。提出了一种非线性二次方程组的求解方法,首先将核问题转化为二次等式的优化问题,引入误差范数约束非凸优化问题,将二次等式进行一阶和二阶泰勒展开,将原问题在局部近似为一个最优化问题并利用迭代凸优化求解,得到雷达探测范围与导弹弹道的交汇点坐标的解析解,实现对雷达探测时间窗口的准确估算。通过场景模拟与求解分析证明了该方法的正确性,并表明该方法具有精度高、通用性强的特点。
弹道导弹;探测;雷达探测窗口;非线性二次方程组;迭代凸优化
在弹道导弹攻防中,为提高弹道导弹突防成功率、减少导弹防御系统预警时间,常在弹道导弹上布置电子战装备以干扰预警雷达探测[1]。导弹在飞行过程中为规避探测常处于电磁静默状态,延迟或滞后释放电磁干扰易暴露目标,故估算预警雷达对弹道导弹探测的时间窗口,选择合适的时间窗口对远程预警雷达进行干扰具有重要的研究意义[2]。
近年来,围绕导弹弹道模型与雷达探测模型的研究不在少数,文献[3~5]等研究了简化的弹道导弹的通用性模型,文献[6]研究了常见导弹发射参数对导弹弹道的影响,文献[7]根据弹道理论建立了雷达探测弹道导弹的仿真模型,文献[8]建立了探测雷达对弹道目标跟踪的数学模型并进行了仿真,文献[9]结合SPY雷达具体特性,分析了雷达对导弹目标的探测效能。但这些研究很少从宏观角度将导弹弹道与雷达探测的数学模型进行结合研究探测时间估算的通用方法。在求解非线性方程时,一般采用迭代最小二乘法、梯度下降法、拟牛顿法等方法[10],这类方法容易导致解的发散,缺乏鲁棒性。本文将雷达对导弹的探测时间估算问题转化为非线性方程组求解的数学问题,通过迭代凸优化的算法进行求解,算法具有较高的精度与较强的通用性。
1 探测模型建立与场景分析
估算远程预警雷达对弹道导弹的探测时间,首先要分析雷达对导弹的探测场景,在综合考虑导弹轨迹模型与雷达探测范围模型的基础上进行分析。
1.1 坐标系建立
本文中导弹发射点与落点的选定、弹道轨道根数的求解和模型建立均在地心惯性坐标系(ECI)下进行,该坐标系以地心O为原点,zE轴沿地球自转轴指向正北方向,xE轴为赤道面与本初子午面交线方向由地心向外,yE轴与xE、zE轴构成右手坐标系。
为简化导弹轨道模型与雷达探测模型联立后的解析表达式,定义坐标系Oxyz(I系),该坐标系以地心O为原点,以发射点A、目标点B连线的中垂线为y轴,方向由地心向外;z轴垂直于OAB所在平面,方向与OA、OB外积方向相同;x轴与y、z轴构成右手坐标系。I系示意图如图1所示。
1.2 探测模型的简化
由于本文主要解决非线性方程组的求解问题,不失一般性,可对导弹运动模型与雷达探测模型作如下简化:根据弹道导弹的飞行时间较短,可忽略其轨道摄动与其自由段运动时间长的特点,将导弹运动模型近似为绕地球质点的二体椭圆运动[11];雷达对弹道导弹进行探测时,在忽略导弹运动过程中目标雷达截面积(RCS)S起伏效应的情况下,可认为雷达对其探测的最大距离保持不变,探测范围可近似看作一个以雷达为中心的球;远程预警雷达大多为地基或海基雷达,部署海拔较低,故可将雷达的探测视线范围近似看作过雷达部署点与地球相切的平面。
1.3 探测场景分析
在上述简化的基础上,将导弹轨迹看作I系Oxy平面内的椭圆曲线;雷达探测范围看作R3中的球体;雷达视线看作与地球相切的平面,在弹道平面Oxy内对雷达的探测场景进行讨论。
1)无法被探测的场景。
在平面Oxy中,雷达探测范围球在该平面内的截面为一个圆。易得当该圆与导弹轨迹相离或相切时,导弹无法被雷达探测,如图2、图3所示。
2)能够被探测的场景。
当雷达探测范围与弹道轨迹存在交点时,位于交点之间的弹道轨迹能被探测,考虑雷达视线对探测范围的遮挡效应与发动机脱离对探测范围的影响,对雷达探测场景进行讨论。
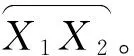
②发动机脱离对雷达探测的影响。 导弹在主动段结束时发动机脱离,弹头继续按椭圆轨迹运动,此时导弹的雷达截面积(RCS)发生较大变化,雷达探测的最大距离改变,对应探测球半径发生改变,此时雷达探测模型在Oxy平面中截面是两段圆心相同的圆弧,记发动机脱离点为P点,脱离前探测圆弧为l1,脱离后为l2,将两段圆弧与导弹轨迹相交的情况分为以下几类进行讨论。


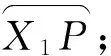
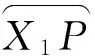
2 探测时间估算的数学模型
估算远程预警雷达对弹道导弹的探测时间问题等效于计算导弹进入与离开雷达探测范围的时刻,该问题的求解需要得到上述关键点的具体位置与导弹运动的时间-位置参数方程。
为方便模型化简计算,在自定义坐标系(I系)下讨论导弹运动模型与雷达探测模型。
简化后的弹道轨迹在自定义坐标系I系中可看作三维椭球在弹道平面上的截线轨迹:
(1)

视线平面在I系中表现为一个与地球相切的平面,被Oxy平面所截得的直线表示为
(2)

雷达探测范围模型是R3中一个球体,表示为
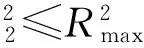
(3)
式中:X∈R3为三维空间内任意点;Rmax为雷达最大作用距离,参考相控阵雷达搜索方程[12]:
(4)
式中:Pav为雷达平均功率;d为雷达孔径;ts为雷达搜索时间;S为目标雷达截面积;L为衰减因子;Ni=kTeBnFn为接收机输出的等效噪声功率;Ωs为搜索空域立体角;D0为检测因子,表示雷达检测所需的最小信噪比。
考虑到导弹在主动段结束时发动机脱离,此时导弹的RCS发生较大变化,雷达探测最大距离改变。对于工作频率10 GHz的雷达,分离前的导弹弹体的RCS量级约为1 m2;分离后的导弹弹头RCS量级约为0.1 m2。记导弹发动机脱离点坐标XP=(xPyP0)T,对应的雷达探测距离分别记做R1max和R2max。故在考虑发动机脱离时,雷达探测范围模型表示为
(5)
将计算导弹在雷达探测范围内的边界点问题转化为一系列方程组的求解问题。
计算视线平面与导弹轨道切点:
(6)
计算发动机脱离前后探测球与导弹轨迹交点:
(7)
(8)
解得各交点后,结合1.3节分析的场景求得实际的探测范围。
得到导弹在雷达探测范围内的边界点后,代入导弹运动的时间-位置参数方程求解雷达探测时间,本文采用常见的椭圆轨道根数模型进行计算。
在ECI坐标中椭圆轨道模型可根据轨道根数(a,e,i,ψ,ω,tP)确定,其中,a为轨道长半轴;e为偏心率;i为轨道倾角,表示轨道平面与赤道平面的夹角;ψ为升交点角距,表示升交点与ECI系中x轴的夹角;ω为近地点角距,表示升交点与近地点之间的夹角;tz为导弹起飞至近地点用时。
确定轨道根数后,可以计算给定时刻t的偏近地点角E(t),进而求得该点的地心距离r(t)。
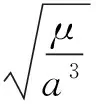
(9)
式中:μ为引力常数与地球质量的乘积。在已知探测范围边界点位置后可由上式反推导弹经过该点的时刻。
3 迭代凸优化求解算法
从上一节中的分析不难看出,估算雷达预警时间的关键在于式(6)~式(8)的非线性方程组求解问题,本文采取的求解方式是将非线性方程的定值求解问题转化为变量优化问题进行计算。
3.1 弹道轨迹与雷达探测范围交点的计算

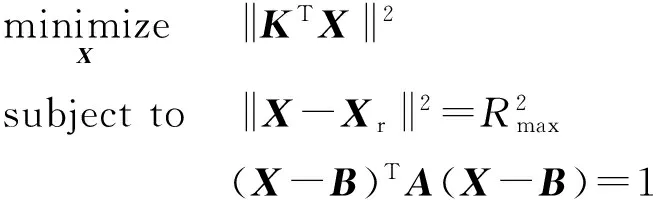
(10)
该优化问题中,约束条件中表示的三维曲面上的点集是非凸集合,由于三维曲面在任意点附近可用过该点的超平面进行近似逼近,将其局部松弛为平面后可对优化模型采取凸优化的算法求解。
对三维曲面函数进行泰勒展开,取其一阶近似:令X=X0+ΔX,f(X)在X=X0处的Taylor展开为f(X)=f(X0)+(f(X0))TΔX+o(ΔX),其中f(X0)为f(X)在X0处的微分;o(ΔX)为在ΔX→0时比ΔX高阶的无穷小。故一阶近似后拟合的超平面方程为f*(X)=f(X0)+(f(X0))TΔX。
不难看出,f*(X)对f(X)的逼近程度与ΔX的取值大小呈负相关,在选取的X0点与所求点相差较大时,一次近似后的运算精度有限,考虑采用迭代算法进行多次迭代优化求解。
在选取初始点X01后,将ΔX1作为变量对问题进行优化求解,将求得的X1=X01+ΔX1作为下一次运算的初始点X02将ΔX2作为变量进行迭代运算,第k步运算表示为
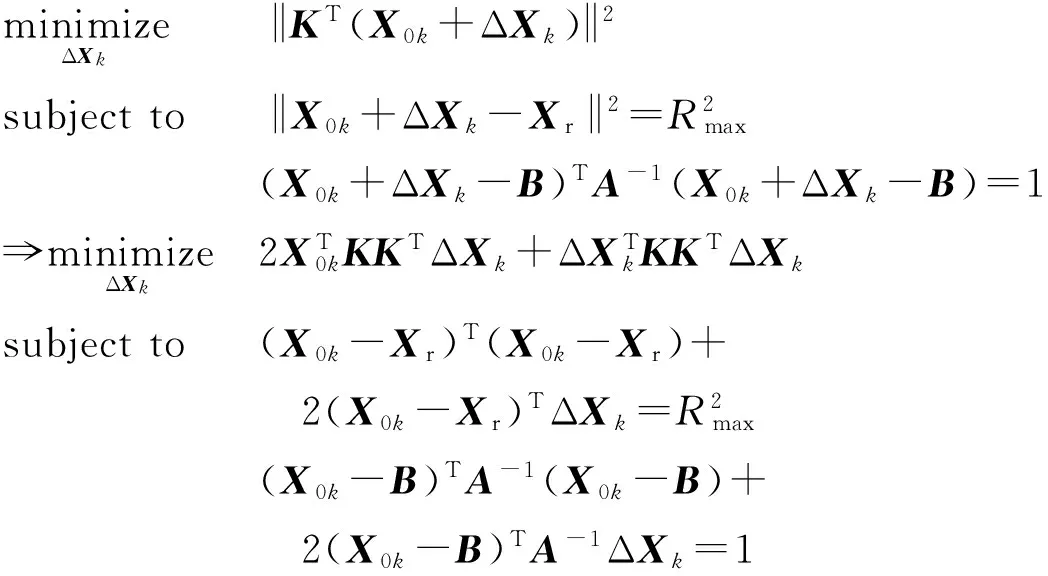
(11)
由第1节中对雷达探测情景的分析可知,在导弹能够被雷达探测到的情况下,雷达探测球与导弹轨迹存在2个交点,即优化问题存在2个全局最优解,在设置迭代初始值X01时,分别在下方交点的下行位置和上方交点的上行位置取初始点以控制优化方向,得到对应最优解。
3.2 视线平面与弹道轨迹交点计算
在确定探测球与椭圆轨道交点后,需进一步求解雷达视线平面与椭圆轨道的交点得到实际探测范围,同理,取式(6)中线性函数的二范数为目标函数,非线性部分为约束条件,将问题转化为优化模型:
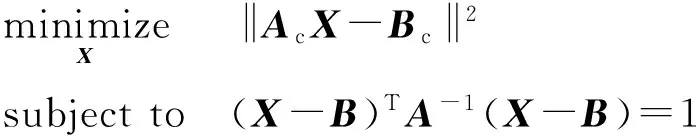
(12)
令X=X0+ΔX,采用相同方法对约束条件松弛后进行迭代凸优化求解,第k步运算表示为

(13)
在迭代初始值选取上,由于只关心靠近视平面线与导弹轨迹靠近雷达一侧的交点,故选择靠近该点的雷达坐标Xr为优化初始值。
以下给出上述采用迭代凸优化方法求解非线性方程组算法的正式描述。
1)任务。
求解非线性方程组。
2)问题转化。
①分离方程组中的线性函数与非线性函数,取线性函数的二范数作为目标函数,非线性函数作为约束条件,将方程组求解问题转化为优化问题:
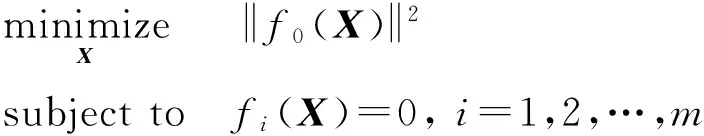
②令X=X0+ΔX,将非线性函数在X0点处进行泰勒展开,取其一阶近似:
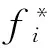
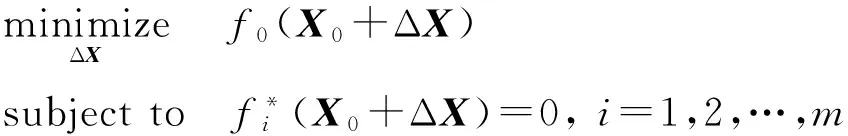
3)迭代求解。
①初始值选取:设定迭代次数k=0,根据求解目标位置,选择该点附近的已知点作为迭代运算的初始点X01;
②迭代次数k增加1,对凸优化问题进行求解,得到ΔXk;
③更新解:计算Xk=X0k+ΔXk
④更新初始值:将新解作为新的优化初始值X0k+1=Xk;
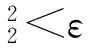
4 场景模拟与仿真分析
为验证上述算法,给出3种场景下的导弹轨迹模型与雷达探测模型,对导弹探测时间进行估算,具体参数如表1所示。表中λ0、φ0、h0分别为导弹发射点北纬纬度、东经经度和高度;λf、φf、hf为落点对应量;tP为发动机脱离时导弹飞行时间;S1、R1max分别为弹头脱离前的雷达截面面积和探测距离;λr、φr、hr为雷达的位置;S2和R2max为弹头脱离后的雷达截面积和探测距离。
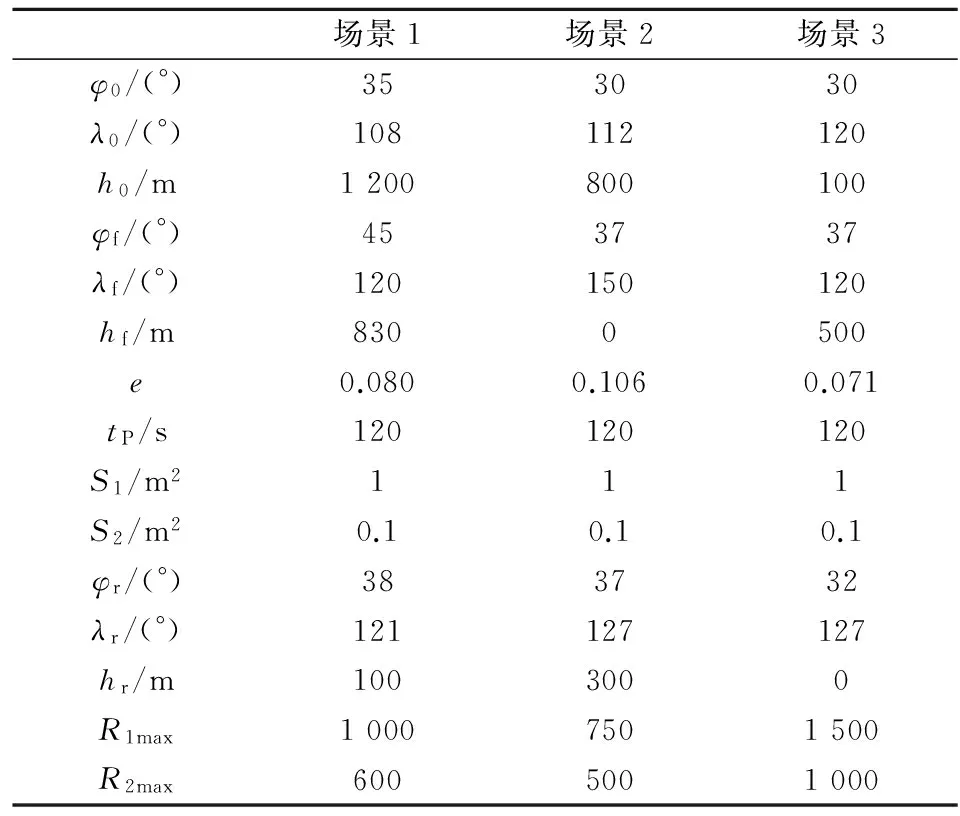
表1 不同场景下探测的关键参数
根据表1参数建立导弹轨迹模型与雷达探测模型,设定迭代终止误差ε=1×10-10,采用迭代凸优化求解算法得到发动机脱离前雷达探测球与导弹轨迹交点X1、X2;发动机脱离后雷达探测球与导弹轨迹交点X3、X4;视线平面与导弹轨迹交点Xc;再通过轨道根数模型得到发动机脱离点位置P,各点在Oxy平面椭圆轨道中的位置关系分别在图10~图12中表示。
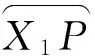
以交汇点与导弹弹道的距离Δ=norm(Xk-B)TA-1(Xk-B)-1作为衡量误差的标准,算法求得各交汇点X1、X2、X3、X4、P的计算误差由表2所示。
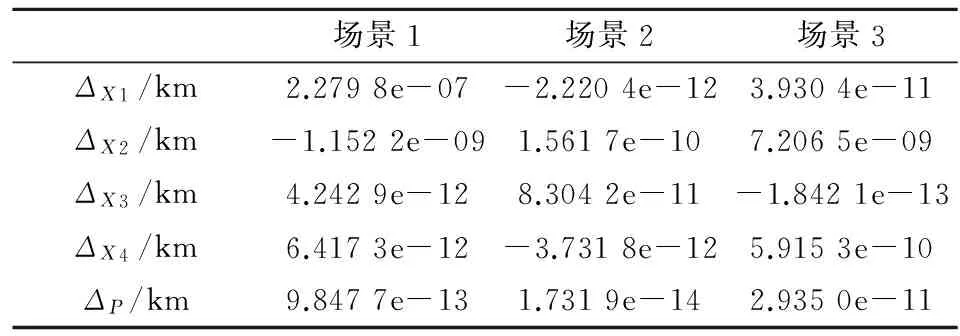
表2 不同场景下算法计算误差
定义导弹发射时间为零时刻,结合导弹根数模型,计算不同场景下雷达对导弹的探测时间窗口,结果如表3所示。表中tb为探测起始时间,te为探测终止时间,Δt为探测总时间。

表3 不同场景下雷达对导弹的探测时间窗口
场景1中的探测时间窗口为导弹发射后105~120 s,总时间为15 s;场景2中由2个探测时间窗口,分别为导弹发射后102~120 s与导弹发射后133~245 s,第一段窗口总时间为18 s,第二段窗口总时间为112 s;场景1中的探测时间窗口为导弹发射后39~206 s,总时间为167 s。
从表1的计算误差与表2对雷达探测时间窗口的计算结果可以看出,本文提出的方法具有较高的计算精度,同时能够在不同的雷达探测情景下实现对探测时间窗口的估计。
5 结束语
分析仿真计算结果,本文提出的迭代凸优化算法能够有效求解非线性二次方程组,适用于不同的探测场景且具有较高的精度。有效地解决了远程预警雷达对弹道导弹探测时间的估算问题。同时该方法对于三维空间目标运动轨迹交点的求解问题具有较强的通用性,在航天器探测跟踪、GPS定位等领域同样具有应用前景。
[1] 金林.弹道导弹防御系统综述[J].现代雷达,2012,34(12):1-7.
JIN Lin.Overview of ballistic missile defense system[J].Modern Radar,2012,34(12):1-7.(in Chinese)
[2] 袁可亮,施自胜,罗金亮,等.弹道导弹突防中的电磁威胁分析及对策[J].舰船电子对抗,2013,36(2):33-34.
YUAN Ke-liang,SHI Zi-sheng,LUO Jin-liang,et al.Analysis and countermeasures of electromagnetism threats in the ballistic missile defense penetration[J].Shipboard Electronic Countermeasure,2013,36(2):33-34.(in Chinese)
[3] LI X R,JILKOV V P.Survey of maneuvering target tracking.Part Ⅱ:motion models of ballistic and space targets[J].IEEE Transactions on Aerospace & Electronic Systems,2010,46(1):96-119.
[4] 曹敏,刘永祥,黎湘.弹道导弹轨迹参数生成技术研究[J].电光与控制,2004,11(2):35-37.
CAO Min,LIU Yong-xiang,LI Xiang.Study on generation of trajectory parameters for ballistic missiles[J].Electronics Optics & Control,2004,11(2):35-37.(in Chinese)
[5] 霍伟,王晓钧.基于弹道仿真的反导系统分析[J].中国电子科学研究院学报,2009,4(5):507-510.
HUO Wei,WANG Xiao-jun.Analysis of antimissile system based on trajectory simulation[J].Journal of China Academy of Electronics and Information Technology,2009,4(5):507-510.(in Chinese)
[6] XU H,CHEN W,NING X.Simulation research on missile tracking under the guidance of online real radar[C]//Asian Simulation Conference.Singapore:Springer,2016:519-531.
[7] 朱力,王盛利,于立.弹道导弹的雷达探测系统仿真[J].计算机仿真,2000,17(1):46-48.
ZHU Li,WANG Cheng-li,YU Li.The simulation of radar detection system of ballistic missile[J].Computer Simulation,2000,17(1):46-48.(in Chinese)
[8] PEDERSEN R N,MOUNTCASTLE P D,VISS S J.Method and system for analyzing ballistic trajectories:IEEE US9342907[R].2016.
[9] 张海成,杨江平,王晗中.舰载SPY雷达对弹道导弹探测效能分析[J].现代雷达,2012,34(1):1-4.
ZHANG Hai-cheng,YANG Jiang-ping,WANG Han-zhong.Analysis of detection performance of shipborne SPY radar for ballistic missile[J].Modern Radar,2012,34(1):1-4.(in Chinese)
[10] 谷晓辉,龚春林,谷良贤.导弹运动方程求解策略研究[J].计算机仿真,2013,30(7):92-95.
GU Xiao-hui,GONG Chun-lin,GU Liang-xian.Strategy study on missile motion equations[J].Computer Simulation,2013,30(7):92-95.(in Chinese)
[11] 肖滨,郭鹏程,衡军,等.战术弹道导弹的弹道仿真[J].系统仿真技术,2008,4(4):213-217.
XIAO Bin,GUO Peng-cheng,HENG Jun,et al.Ballistic simulation of tactical ballistic missile[J].System Simulation Technology,2008,4(4):213-217.(in Chinese)
[12] 张光义,赵玉洁.相控阵雷达技术[M].北京:电子工业出版社,2007.
ZHANG Guang-yi,ZHAO Yu-jie.Phased-array radar techn-ology[M].Beijing:Publishing House of Electronics Industry,2007.(in Chinese)
EstimationMethodofMissileDetectionTime-windowBasedonIterativeConvexOptimization
GE Rui-xing,ZHOU Qing-song,ZHANG Jian-yun,CHEN Shi-wa
(School of Electronic Countermeasure,National University of Defense Technology,Hefei 230037,China)
To accurately estimate the time-window of long-range early-warning radar dectecting ballistic missile,the simultaneous mathematical model of missile trajectory and radar detection-range was built,and a method of solving the nonlinear quadratic equations was proposed.The core problem was transformed into an optimization problem,and the error norm was introduced to constrain the non-convex optimal problem.The first and second order Taylor expansion of the quadratic equation was carried out,and the original problem was approximated to an optimization problem locally,and the iterative convex optimization was used to solve the problem.The analytical solution of radar detection-range and trajectory joint-point were obtained to realize the accurate estimation of radar detection time-window.Scene simulation and solution analysis prove that the method is correct,and this method has the characteristics of high precision and versatility.
ballistic missile;detection;radar detection time-window;nonlinear quadratic equations;iterative convex optimization
TJ765.4
A
1004-499X(2017)04-0022-07
2017-05-25
葛瑞星(1993- ),男,硕士研究生,研究方向为导弹实际过程中的电子对抗技术。E-mail:geruixing1993@sina.com。
