非合作目标超近距离光学相对导航方法及半物理仿真系统研究

彭 杨，张翰墨，王兆龙，曹姝清，刘宗明，武海雷

(1.上海市空间智能控制技术重点实验室,上海 201109； 2.上海航天控制技术研究所,上海 201109)

非合作目标超近距离光学相对导航方法及半物理仿真系统研究

彭 杨1,2，张翰墨1,2，王兆龙1,2，曹姝清1,2，刘宗明1,2，武海雷1,2

(1.上海市空间智能控制技术重点实验室,上海 201109； 2.上海航天控制技术研究所,上海 201109)

针对非合作目标研究了一种可实时应用的超近距离相对导航方法，用相机主动获取目标飞行器图像，对图像进行预处理得到有效的边缘段信息。选取立方体卫星作为非合作目标的通用模型，用轮廓精化提取方法进行轮廓的三维重建，并给出了轮廓三维位置和姿态估计信息获取的具体步骤。建立了用四元数和相对欧拉角表示的追踪器与目标器相对姿态的轨道动力学模型，设计了基于衰减扩展卡尔曼滤波的相对导航算法。构建了一套基于运动导轨的半物理仿真系统，以验证算法的有效性和可行性。给出了仿真系统的硬件组成和软件功能。结果表明：所建仿真系统获得的相对距离10～0.5 m内非合作目标相对位姿精度分别为0.03～0.15 m，0.5°～1.5°，可用于非合作目标超近距离相对导航研究的相关验证；用所提方法可实现非合作目标的实时超近距离相对导航，能同时获得位姿及相关速度类导航信息，精度满足工程要求。该仿真系统在工程中有较大的应用价值。

非合作目标； 超近距离； 光学相对导航； 轮廓精化； 相对位姿； 衰减卡尔曼滤波； 半物理仿真； 位姿精度

0 引言

空间技术的应用领域在近一二十年中得到了快速发展，除在空间科学应用方面得到继续深入外，在空间对抗、空间服务等领域对空间技术提出了新的需求和任务，其中针对超近距离非合作目标的在轨操作技术因其在民用等不同领域中的潜在价值，已被广泛重视。利用在轨操作技术能对发生故障失效与燃料耗尽寿命终结的卫星等非合作目标实施在轨捕获、元器件更换、燃料加注和助推离轨等操作，可极大地延长卫星的使用寿命，大幅节省卫星的研制成本，有广泛的应用价值。文献[1]对空间非合作目标近程自主跟踪的全局鲁棒最优滑模控制方法进行了研究。但实现超近距离在轨操作的基础是飞行器间的精确相对导航信息，从目前的研究现状来看，国内外基于光学的相对导航技术已日臻成熟，其中美国的自主交会验证试验(DART)通过先进视觉制导敏感器(AVGS)测量距离200 m以内合作目标的相对距离、视线角和目标相对姿态信息；中国的空间站计划已实现了合作目标的交会对接。但上述科学探测计划多数配备LED灯或反射器。针对非合作目标的光学导航，一种方法是采用二维影像与目标的三维模型投影进行匹配测量，无需目标有主动靶标，可用于远小目标的测量，但需事先测量目标的三维模型，计算量巨大，难以进行实时在轨应用[2]。因此，亟需研究一种针对非合作目标可实时应用的超近距离相对导航方法，并通过半物理仿真平台对其实时性进行验证。

本文将通用的立方体卫星作为非合作目标的通用模型，无需在目标背景中建立测量标志，通过相机主动获取其图像信息，在经过图像处理获得六维位置姿态信息的基础上，结合光学相对导航算法，构建一套半物理仿真系统，为飞行器在轨操控提供可靠的先验信息。

1 光学超近距离图像处理技术

将立方星模型置于六自由度坐标平移台上，用光学相机对其成像并实时传输图像至后端嵌入式计算机进行相应图像处理。先对非合作目标进行图像预处理，获取有效的边缘段，图像预处理阶段对所有非合作目标具通用性。在获得有效的边缘段后，形成一个连续的轮廓信息，可以是圆形、方形、矩形或三角形等。本文采用了通用的立方星构造，故为方形。目标卫星模型如图1所示。

获得轮廓信息后，用轮廓精化提取方法进行轮廓的三维估计，从而可得到目标的相对位置与姿态信息[3-4]。

1.1 轮廓三维估计(重建)方法

a)对目标卫星轮廓的角点按顺时针方向排序，并以右下角的点作为起点，则左右影像上相同编号的轮廓角点即为同名点。通过前方交会可得4个角点的三维坐标，令其分别为Ui=[XiYiZi],i=1,2,3,4。

c)计算矩阵

(1)

d)对N进行奇异值分解，则分解所得的最小奇异值对应的特征向量即为目标卫星轮廓的法向量，令其为

n=[nxnynz]T

(2)

其中nz>0。

e)根据目标卫星轮廓的两个方向，可易估计与法向量垂直的和与卫星轮廓尽可能平行的两个单位向量p，q(两个向量的方向选择须保证与n构成右手系)，p，q，n构成目标卫星本体坐标系的三个轴向，从而也确定了目标卫星的姿态。则目标卫星的姿态可表示为

M=[pqn]

目标卫星的姿态可用三个角度表示，即

M=M(φ,ω,κ)

式中：φ,ω,κ分别为绕p，q，n所在轴旋转的角度[5]。

f)根据前面的4个角点可进一步估计目标卫星轮廓4个角点构成的正方形的半边长(边长的一半)。

g)根据以上计算，能估计目标卫星轮廓的所有参数，4个角点可表示为

(3)

W1=[h-h0]T

W2=[-h-h0]T

W3=[-hh0]T

W4=[hh0]T

式中：[txtytz]T为目标卫星坐标系与相机固联坐标系间的坐标平移量。此处：h为卫星轮廓边长的一半。

h)将式(3)代入共线方程，可得误差方程为

(4)

式中：a1,a2,a3,b1,b2,b3,c1,c2,c3为摄影坐标系与相机固联坐标系间的旋转系数；Xs，Ys，Zs为摄影坐标系原点在相机固联坐标系中的坐标；f为镜头焦距[6]。

i)分析上述的误差方程可知：式(4)状态量为φ，ω，κ，h，tx，ty，tz。则可令上述误差方程为

Vi=Fi(φ,ω,κ,h,tx,ty,tz)

(5)

对式(5)用泰勒级数展开并作线性化处理。

j)对4个轮廓角点，考虑左右影像，可列出线性化误差方程共8个，则用矩阵形式表示的误差方程为

V=F+AΔX

(6)

式中：ΔX为误差方程的状态量(待求量)；F为式(5)泰勒展开式中的一阶项；A为状态转移矩阵[7]。

k)用最小二乘法求解式(6)，可得

ΔX=-(ATA)-1ATF

(7)

l)由此可修正卫星轮廓的参数。若修正量已很小，则可认为已得到了卫星轮廓参数的最优估值，否则需返回进行下一次的迭代计算。

1.2 位姿信息获取方法

a)通过左右影像的相机参数和核线约束方式获得初始的同名点数个，再用摄影测量前方交会方法，即可得若干个点的三维坐标[8]。

b)计算求得的若干个点的三维坐标的重心，可得轮廓所在平面的法向量，再确定一个与所在平面法向量垂直的平面向量，叉乘后得到第三个向量。由这三个向量可确定卫星的姿态角信息[9]。

c)通过轮廓提取与几何解算获得提取点在轮廓所在坐标系中的坐标，并根据相对姿态信息获得的旋转矩阵表示出在空间的三维坐标。

d)用共线方程多次迭代对空间轮廓信息的参数进行修正，从而获得位姿信息。

2 光学超近距离相对导航技术

对相机采集的图像用图像，处理算法生成相对位姿信息，将相对位姿信息作为量测量，待求的相对位置、速度，相对姿态及角速度信息作为状态量，用卡尔曼滤波算法获得其最优值。为实现星上应用，需考虑运算量，一般卡尔曼滤波时刻k最优估计需用到时刻k前全部观测数据，随着观测时间的增加，数据解算量大幅增加。为此，本文引入衰减因子增大当前数据的权系数，可一定程度克服历史数据庞大的问题，同时不断更新的新观测数据能使误差对状态估值的影响有效一致。

2.1 相对姿态轨道动力学建模

追踪星与目标星的相对姿态可用相对四元数描述，有

(8)

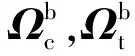
(9)

为使相对导航描述更直观，将相对四元数转换至相对欧拉角描述，并对角度奇异性进行分析。有

(10)

(11)

若cosψ=0，则

(12)

式中：φ为滚动角；θ为俯仰角；ψ为偏航角。

定义相对角速度为追踪星本体相对目标星本体的相对旋转角速度在追踪星本体系中的表示，有

ωr=ωc-Ccb/ctωt

(13)

式中：Ccb/ct为由目标星本体系至追踪星本体系的转换矩阵；ωr为相对角速度；ωc，ωt分别为追踪星和目标星角速度。

对式(6)求导并用矩阵形式表示，有

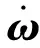
(14)

简化可得

(Ic)-1[Tc-(ωc)×Icωc+Dc]+(ωr)×ωc

(15)

式中：Ic为追踪星转动惯量矩阵；Tc，Dc分别为作用于追踪星的控制力矩和干扰力矩；上标“×”表示斜对称矩阵。

相对轨道动力学采用简化的CW方程表示[10]。则有

(16)

2.2 相对导航算法

因系统本身的非线性特性，理论上难以获得严格的递推滤波公式，故目前常采用近似方法研究非线性滤波的线性化。为解决这类问题，现有的方法有扩展卡尔曼滤波、近似条件均值滤波、迭代滤波和非线性最小二乘滤波等。本文采用衰减记忆扩展卡尔曼滤波方法。随着增益的增大，传统卡尔曼滤波中的历史数据比重增大，而新数据比重变小，当系统存在模型误差和计算误差时，新观测数据对状态估计的作用过小，不能有效抑制误差对状态估值的影响，从而导致滤波发散。针对模型误差引起的滤波发散，应增大新观测数据的作用，引入观测数据的权重因子[11]。

非线性连续系统方程可表示为

(17)

式中：ω(t)为系统状态噪声。

若相对欧拉角较小，可简化为

(18)

u=U(Ic)-1(Tc-(ωc)×Icωc+Dc)-

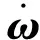
式中：μ为相对欧拉角速度；ucx，ucy，ucz为追踪星三轴控制力。对式(17)作线性离散化，可得

Xk+1=ΦXk+ωk

(19)

式中：Φ为状态一步转移矩阵；ωk为随机过程噪声序列。

将图像处理所得的相机的相对位姿输出值作为观测量，双目视觉测量模型为

(20)

式中：Δμm为相对角度测量值；Δρm为相对位置测量值；v(t)为测量噪声。

线性观测模型离散化后可得

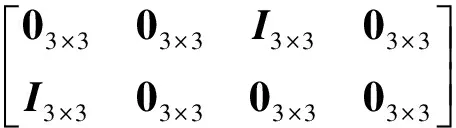
综合上述相对导航动力学模型、观测模型，经线性化处理，由扩展卡尔曼滤波可给出衰减记忆扩展卡尔曼滤波模型[12]。

式中：s为大于1的实数，即衰减因子。此处s的上标-(N-k)为幂指数，可得状态估计、状态一步预测、滤波增益、一步预测误差方差矩阵，以及估计误差方差矩阵分别为

式中：T为采样周期。

由此可知：衰减记忆的滤波器中因引入s(s>1)使新的量测值的利用权重加大，但s的值不宜选取过大，否则会引起滤波器的振荡，必须合理选择。

3 相对导航半物理仿真系统设计

实时高精度的地面半物理试验是验证光学导航方法可靠性的一种有用途径，本文在图像处理与相对导航算法设计的基础上构建了一套基于运动导轨的相对导航半物理系统。

3.1 系统组成

3.1.1 硬件

相对导航半物理仿真系统主要由高精度六自由度坐标平移台、高精度可拼接导轨和相机平移转台等部分组成，如图2所示。

立方星安装在固定位置，相机安装在六自由度坐标平移台上，相机的姿态和位置运动由六自由度坐标平移台实现，并通过六自由坐标平移台相应自由度的码盘读取相机的姿态与位置运动信息。通过可拼接导轨扩展坐标平移台沿相机光轴方向(Z向)的测量范围，坐标平移台在可拼接导轨上以移动工位的方式工作，测量过程中Z向的运动主要由六自由度坐标平移台实现，坐标平移台在可拼接导轨上的具体位置通过磁尺进行测量。相机平移转台实现相机所在坐标系X向的移动和绕Z轴的转动，从而扩展并覆盖视觉测量系统所达到的视场范围，X向移动和Z轴转动的位移信息由磁尺与码盘测得。

3.1.2 软件

根据实施过程中设计和调整的数据解算方案，设计的软件包括通信交互、图像镜头畸变纠正与图像增强、边缘检测与特征提取、卫星轮廓三维估计、目标卫星位置与姿态解算、数据转换，以及存储与显示等模块。其中：通信交互模块实现各模块间数据传输；图像镜头畸变纠正与图像增强模块完成目标图像预处理；边缘检测与特征提取模块负责目标特征检测；卫星轮廓三维估计模块进行目标相对位姿测量。

3.2 试验流程

试验流程如下。

a)精确标定视觉敏感器各参数。

b)动力学目标机将动力学信息下载到主机目标机构原型环境(XPC)，并实时传输至导轨控制台，模拟相对运动的过程。

c)导轨运动过程中，相机采集的图像经图像处理软件生成位姿信息，实时传输至嵌入式计算机。嵌入式计算机根据预先写入的相对导航软件解算。

d)嵌入式计算机的相对导航信息接入姿态轨道控制中，形成整套闭环系统。其中姿态轨道控制系统无实物，只用C语言写入嵌入式计算机。

e)通过显示终端显示相对导航精度曲线。

3.3 半物理仿真

3.3.1 仿真试验系统标定

综合考虑相对测量光学敏感器仿真试验系统测试标定精度和成本，将全站仪或经纬仪作为外测精密设备，在经纬仪/全站仪坐标系中，比较相对测量光学敏感器和经纬仪/全站仪的六自由度数据，完成相对测量光学敏感器仿真试验系统的标定[13]。所得仿真试验系统性能参数为行程10 m；X、Y、Z轴精度分别为0.1，0.1，0.5 mm；X、Y、Z轴转动精度分别为0.02°，0.024°，0.005°。

3.3.2 仿真试验结果

令航天器初始轨道要素见表1。设仿真中追踪航天器从目标航天器正后方10 m接近至目标0.5 m，仿真试验所得10～0.5 m范围内图像处理获得的相对位姿测量精度如图3所示。根据测量数据，用本文滤波及相对导航算法所得相对位姿及其相应速度如图4所示。图4中：R为两航天器相对距离。

轨道要素半长轴/m偏心率轨道倾角/(°)升交点赤经/(°)近地点幅角/(°)真近点角/(°)目标航天器6945140000197654697830561253601追踪航天器69451400001976546978305612536

由图3可知：用本文搭建的相对导航半物理仿真系统，可实时获得相对距离10～0.5 m非合作目标的相对位姿信息，其中相对位置的测量精度可达0.03～0.15 m，相对姿态角的测量精度优于0.5°～1.5°。由图4可知：由本文的基于衰减记忆扩展卡尔曼滤波的相对导航算法，可获得相对距离10～0.5 m非合作目标的相对位姿及相关速度信息，其中相对位置三轴导航精度、相对速度三轴导航精度、相对姿态精度(三轴)，以及相对姿态角速度精度(三轴)分别优于

0.05+0.006(R-0.5) m

0.005+0.000 6(R-0.5) m/s

1+0.04(R-0.5) (°)

0.2+0.008(R-0.5) (°)/s

综上，采用衰减记忆卡尔曼滤波算法，在有效降低运算量的基础上，不仅可得到与半物理仿真系统精度相当的相对位姿信息，而且能获得速度类导航信息，所提的相对导航算法有效；构建的半物理仿真系统可用于非合作目标超近距离相对导航研究的验证。但本文半物理仿真系统尚存在一定的局限性：受平移台移动范围及性能的限制，非合作目标的运动范围较小且仅为平行移动；本文是仅采用立方星模型作为非合作目标的原型获取的半物理仿真结果。针对以上局限性，后续将针对实际空间运行，对该套仿真系统作进一步改造。

4 结束语

非合作目标的超近距离相对导航是空间在轨操控的核心，直接关系任务的成败。本文对非合作目标的超近距离相对导航方法进行了研究，并搭建了光学超近距离相对导航半物理仿真系统。研究表明：用本文的非合作目标超近距离光学相对导航方法可获得非合作目标的相对位姿及其速度类信息，精度满足要求，能实现非合作目标的实时超近距离相对导航；半物理仿真系统能对非合作目标进行实时图像识别及导航，可用于非合作目标超近距离相对导航算法研究的验证。目前，该系统已用于民用航天、国家863等多个项目的验证。与前人成果相比，本文算法的计算量小，能用于嵌入式计算机，搭建的半物理仿真系统可模拟空间运动及日照环境，有一定的工程实用性[14]。研究为后续空间技术发展和应用提供了重要支撑。

[1] 王洪宇, 杨雪勤, 贡鑫. 空间非合作目标近程自主跟踪的全局鲁棒最优滑模控制研究[J]. 上海航天, 2017, 34(3): 88-94.

[2] 蔡伟, 柯文贡, 坚习飞. 一种基于模型的单相机姿态估计方法[J]. 中国图象图形学报, 2008, 13(3): 513-518.

[3] 崔亚奇, 宋强, 何友. 系统偏差情况下的目标跟踪技术[J]. 仪器仪表学报, 2010, 31(8): 1848-1854.

[4] 魏建勇, 王进花, 曹洁, 等. 基于ISPF与异类信息融合的视觉目标跟踪[J]. 国外电子测量技术, 2009, 28(9): 26-28+34.

[5] 张庆君, 胡修林, 叶斌, 等. 基于双目视觉的航天器间相对位置和姿态的测量方法[J]. 宇航学报, 2008, 29(1): 156-161.

[6] 丁尚文, 王惠南, 刘海颖, 等. 基于对偶四元数的航天器交会对接位姿视觉测量[J]. 宇航学报, 2009, 30(6): 2145-2150.

[7] TSAI R Y. A versatile camera calibration technique for high accuracy 3D machine vision metrology using off the shelf TV cameras and lenses[J]. IEEE Journal of Robotics and Automation, 1987, 3(4): 323-344.

[8] 郑南宁. 计算机视觉与模式识别[M]. 北京: 国防工业出版社, 1998.

[9] 张广军. 视觉测量[M]. 北京: 科学出版社, 2008.

[10] 朱仁璋. 航天器交会对接技术[M]. 北京: 国防工业出版社, 2007.

[11] 张世界. 一种新的检测方法在目标跟踪中的应用[J]. 电子测量技术, 2009, 32(5): 82-84+123.

[12] 宋文尧, 张牙. 卡尔曼滤波[M]. 北京: 科学出版社, 1991.

[13] 张智强. 基于靶标成像双目视觉坐标测量技术的研究[D]. 上海: 上海大学, 2004.

[14] 王久龙. 基于动态实时立体匹配的立体视觉系统[D]. 杭州: 浙江大学, 2008.

StudyonRelativeVisionNavigationMethodandSemiPhysicalTestSystemforNonCooperativeTarget

PENG Yang1, 2， ZHANG Han-mo1, 2， WANG Zhao-long1, 2，CAO Shu-qing1, 2， LIU Zong-ming1, 2， WU Hai-lei1, 2

(1. Shanghai Key Laboratory of Aerospace Intelligent Control Technology, Shanghai 201109, China;2. Shanghai Institute of Spaceflight Control Technology, Shanghai 201109, China)

A relative navigation method was studied for the non cooperative target with close distance in real time in this paper. The image of the target was acquired by the camera actively. The image was pretreated to obtain the effective information of the target edge. The cube satellite was selected as the general model of the non cooperative target. The three dimension estimation (reconstruction) of the edge was carried out to obtain the relative position and attitude between the tracker and target by the outline refinement method. The steps to acquire the three dimension estimation of the edge and the estimation of the relative position and attitude were given. The orbit dynamic model of the relative attitude of the tracker and target was established by quaternion and relative Euler angles. The relative navigation algorithm was designed based on fading Kalman filter. A semi-physical simulation test system was constructed based on motion guide rail, which was used for verifying the effectiveness and feasibility of the algorithm proposed. The hardware and software of the semi-physical test system were presented. The results show that the accuracies of the relative position and attitude obtained by the simulation system constructed can reach 0.03～0.15 m and 0.5°～1.5° respectively for the relative distance of the non cooperative target from 10 to 0.5 m. The semi physical test system can be used for the verification of the relative navigation study for non cooperative target with close distance. The close distance navigation of the non cooperative target can be realized in real time by the algorithm proposed. The relative pose informationn and their velocity information can be obtained at the same time. This semi physical simulation test system has its application value in the engineering.

non cooperative target; close distance; relative navigation based on vision; outline refinement; relative position and attitude; fading Kalman filter algorithm; semi-physical simulation test; accuracy of position and attitude

1006-1630(2017)06-0076-07

V448.2

A

10.19328/j.cnki.1006-1630.2017.06.012

2017-07-12；

2017-11-30

上海市科技人才计划项目资助(14QB1401800)

彭 杨(1985—)，女，硕士，主要研究方向为航天器导航、制导与控制。