基于亚像素边缘检测的高精度圆孔参数测量方法研究

钱 斌，郭国强，邱 磊，王福伟，金 露，伏燕军

(1.南昌航空大学 无损检测技术教育部重点实验室,江西 南昌 330063；2.上海航天精密机械研究所,上海 201600)

基于亚像素边缘检测的高精度圆孔参数测量方法研究

钱 斌1，郭国强2，邱 磊1，王福伟1，金 露1，伏燕军1

(1.南昌航空大学 无损检测技术教育部重点实验室,江西 南昌 330063；2.上海航天精密机械研究所,上海 201600)

为改善用机器视觉对圆孔参数测量结果，减小误差，在利用圆形标定板标定像素当量的基础上，对一种基于亚像素边缘检测的高精度圆孔参数测量方法进行了研究。用改进的Zernike矩亚像素边缘检测方法对边缘点作进一步的细化和筛选，用7×7模板替代原5×5模板，设计新阈值判断标准检测亚像素边缘，再对检测到的边缘点偏离像素进行抑制以获得更精确的图像边缘点；用最小二乘法进行圆形拟合获得圆形参数。给出了改进算法的基本步骤。用实验讨论了在自然光条件下，相机曝光亮度，以及相机与被测物体距离对测量结果的影响。结果表明：改进的方法对环境适应性强，易实现，曝光亮度30～50时测量精度较好；相机与物体距离50～60 cm时，测量精度可达0.02 mm。该法在高精度的工业检测中有广泛的应用前景。

圆孔参数测量； Zernike正交矩； 亚像素边缘检测； 最小二乘拟合； 标定板； 像素当量； 曝光亮度； 边缘点

0 引言

航天工业中，常需要在无装夹状态下对加工后的工件上的圆孔位置与尺寸(如圆心及半径等几何参数)进行检测，将最终的测量数据导入CAD软件与原始设计数据进行比对，如有误差，可控制反馈系统进行补偿。目前，国内多数厂家采用人工方法检测工件上的圆孔几何参数。该方法检测效率低、精度低、成本高。圆孔在航天工件上大量存在，因此研究快速、高精度的圆孔测量系统和测量算法对航天工业生产有重要意义，其中基于机器视觉的圆孔参数测量在自动化检验和装配领域将有广泛的应用前景[1-3]。

获取图像的边缘信息和像素当量标定是基于机器视觉测量方法的两个重要方面。边缘点定位的准确性会影响最终的检测结果，而像素当量是单个像素对应的实际物理距离，像素当量标定的准确性直接影响测量精度[4-6]。常用的边缘检测方法是利用灰度图像的一阶或二阶导数进行边缘定位。一阶微分图像边缘检测算子通常是基于对图像梯度的幅值进行阈值化提取边缘，常用的一阶导数算子有Sobel算子、Roberts算子和Prewitt算子[7-9]。一阶导数算子计算简单、抗噪能力弱，易将噪声误检为边缘。二阶微分边缘检测算子通常用于计算图像的二阶方向导数的零交叉点或极值位置，将其作为检测图像的边缘。经典二阶微分边缘检测算子主要有Laplacian算子、Log算子和 Canny算子等[10-11]。其中：Laplacian算子对噪声较敏感，检测时受噪声影响常出现错误边缘；Log算子是对Laplacian算子的改进，但检测边缘与消除噪声存在矛盾；因加入了非极大值抑制和形态学连接操作，Canny算子提取的边缘最完整且边缘连续性较好[11]。上述算子定位精度均是像素级。近年来随着对测量精度要求的提高，传统边缘检测算子已不能满足高精度测量的要求，研究图像亚像素细分算法有重要的意义。文献[12]提出用空间矩检测边缘，但其计算量较大且易出现多余的信息。文献[13]提出用 Zernike矩进行边缘检测。该算法只需要Zernike 矩3 个就可计算出参数4 个，计算速度较快，因此受到了广泛关注。传统Zernike矩边缘检测算法未考虑模板效应，定位精度较低。文献[14]在考虑模板效应的基础上检测图像的亚像素边缘，由于采用传统的边缘判断条件导致检测到的边缘较粗。文献[15]在计算7×7模板的基础上改进了传统边缘判定条件，获得了较细的边缘，但因阈值变化对检测结果影响较大，导致调节较难。文献[16]综合Canny 算子和Zernike 矩亚像素边缘定位，用最小二乘椭圆拟合法定位微零件的中心位置，但其进行亚像素定位时使用了传统Zernike矩亚像素定位算法，边缘定位精度较低。本文在文献[14-22]的基础上，提出了一种改进的Zernike矩亚像素边缘检测方法。研究了新的阈值判断条件，并对检测出的边缘点进行细化和筛选，得到较精确的亚像素边缘点，再用最小二乘法拟合圆孔，检测圆孔参数，并分析了自然光条件下用本文算法测量时相机曝光亮度，以及相机与被测物体距离对测量精度的影响。

1 基于Zernike矩亚像素边缘检测方法

1.1 Zernike矩

图像f(x，y)的二维Zernike 矩可表示为

(1)

式中：m，n为整数，同时满足条件n≥0,n-|m|为偶数且|m|≤n；Vnm(ρ,θ)为积分核函数；ρ为原点至像素(x，y)的向量距离；θ为ρ，x间逆时针方向的夹角[13]。

在离散条件下，图像f(x，y)的二维Zernike矩在满足x2+y2≤1条件下也可表示为

(2)

1.2 Zernike矩边缘定位

(3)

亚像素边缘定位的基本模型如图1所示。其中：圆为单位圆；直线L为边缘上的直线，圆内L两侧的灰度值分别为s，s+t；t为灰度差；l为原点至边的理论距离；α为l与x的夹角。图1(a)中的两条虚线段ab，cd对应在不同阶次的Zernike矩条件下的图像边缘，l1，l2为原点距线段ab，cd的距离。

根据旋转不变性，并考虑模板的放大效应，可得亚像素边缘检测公式为

(4)

式中：(xs，ys)为边缘的亚像素坐标；(x，y)为未细化的坐标点；N为模板大小。

2 改进的Zernike矩亚像素边缘检测方法

传统Zernike矩边缘检测用三个矩

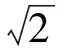
步骤1)计算7×7的模板[M00,M11,M20,M31,M40]。

步骤2)将步骤1算得的模板与原图像进行卷积计算得[Z00,Z11,Z20,Z31,Z40]。

步骤3)计算α。

步骤4)计算l1，l2，l。此处l=(l1+l2)/2。

步骤5)计算s，t。

步骤7)确定图像中满足|t|≥τ的像素点，定为边缘点。

步骤8)用式(4)对得到的边缘点进行细化，得到亚像素边缘点坐标。

步骤9)对步骤8获得的边缘点进行抑制：若细化的边缘点坐标偏离像素值过大则舍去，在此设置最大允许偏离0.5像素。

步骤10)保存步骤9中得到的亚像素边缘点坐标并对图像进行分块，用最小二乘拟合法拟合所得的边缘点坐标分块，得到各圆的边缘、圆心坐标和半径。

为验证改进的Zernike矩亚像素边缘检测方法的有效性，在其他实验条件相同的情况下，用本文提出的算法和传统Zernike矩算法对同一幅图进行检测，测量结果如图2 所示。

由图2可知：用本文的改进算法对边缘进行检测，由于改变了阈值判断条件并加入了对边缘点的抑制，检测得到的是部分精确的边缘点，细化了边缘；传统算法虽然可检测出较完整的边缘但边缘点定位精度较差，伪边缘点数量较多，用检测到的边缘点进行圆拟合时的效果较差。

3 实验结果与分析

测量系统由CCD相机、位移导轨、圆形标定板和台式电脑组成。其中：CCD相机为basler acA1600-20gm相机，分辨率为1 626×1 236像素，搭载焦距16 mm的工业镜头； 2.8 GB内存台式电脑1台；圆形标定板1块，圆心距18.747 mm，半径2.514 mm，这些参数用二维影像仪得到。实验时不使用特殊光源，利用实验室自然环境光源。

先对相机进行垂直度标定，然后采集图片。本文共采集图片4组，每组有图3幅，同组3幅图片的曝光亮度相同，其中：第一组图片曝光亮度0～125；第二组图片曝光亮度0～75；第三组图片曝光亮度0～50；第四组图片曝光亮度0～25。此处：曝光亮度定义为通过调节相机曝光度改变相机接收到的图像亮度。一般情况下，曝光度越大，相机接收到的图像亮度越大，曝光亮度也就越大。

3.1 第一组图片测量对比实验

为分析相机至标定板中心的距离对测量结果的影响，对第一组图片，在相机与标定板距离分别为60，80，100 cm条件下采集图片，所得标定板图像如图3所示。

用本文算法检测距离60 cm(图3(c))的中心区域9个圆，结果如图4所示。根据图4算得的圆半径及圆心坐标见表1。计算中心圆圆心至其周边8个圆心的像素距离，已知圆心间的实际长度，通过计算实际长度与像素距离的比值，可得8个像素当量，计算其平均值得到像素当量0.163 9 mm。平均半径长度15.564 1像素，其半径的平均物理长度2.551 0 mm，标准长度2.514 mm，误差0.037 0 mm，圆心的测量误差0.015 2 mm。

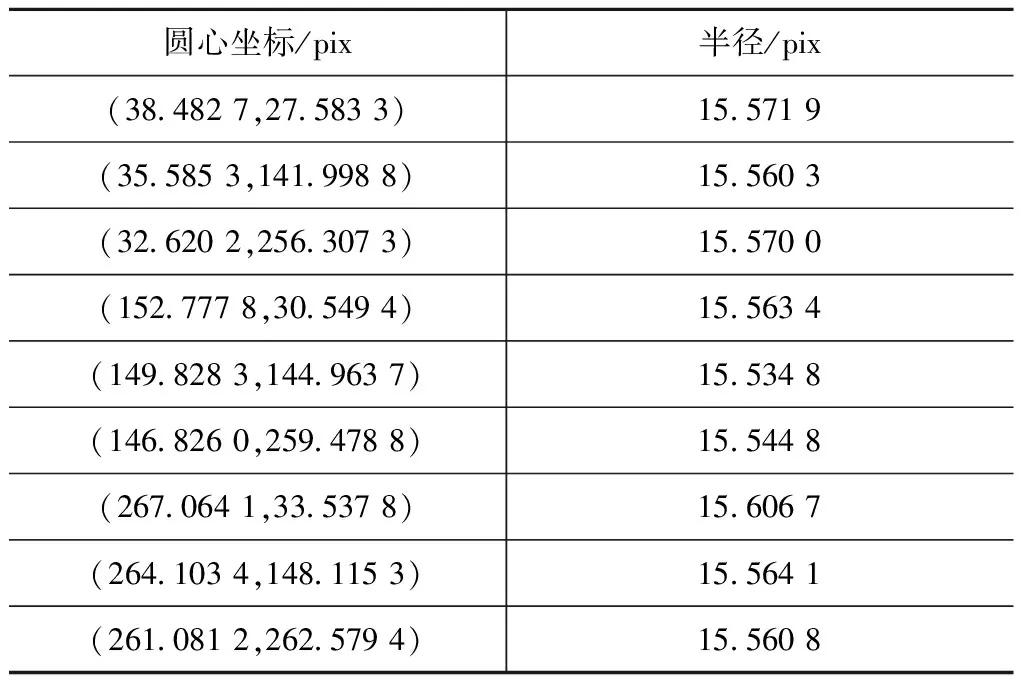
表1 圆半径长度及圆心坐标

用相同计算方法可得距离80，100 cm时的像素当量分别为0.212 1，0.261 8 mm；半径平均物理长度2.569 7，2.597 2 mm。

当图像分辨率分别为300× 300，250×250，200×200时，在Matlab平台上计算并显示结果的时间分别为0.073 ，0.070 ，0.066 s。

3.2 其余三组图片测量对比实验

为进一步分析相机曝光亮度、相机和被测物体

距离对测量精度的影响，在实验室其他条件相同的情况下，利用其余三组图片对圆形半径长度进行对比检测，所得第二、三、四组标定板图像分别如图5～7所示。用相同方法算得三组不同像素当量和实验圆形半径误差分别见表2、3。由表3可知：当灰度相同时，相机与被测物体距离越远，测量精度就越低；灰度越低，测量精度越高。因此，用本文算法进行测量时，当曝光亮度不变，物体与相机距离增大，会降低其测量精度；当距离不变，曝光亮度较低时会获得较高的测量精度。

3.3 实际圆孔测量实验

用本文方法对平均内半径2.5 mm的小圆孔和平均内半径11.19 mm的大圆孔进行测量，内半径值由三坐标测量机得到。圆孔如图8所示。

组别像素当量/mm距离60cm距离80cm距离100cm201639021520268130164002117026794016340212002682

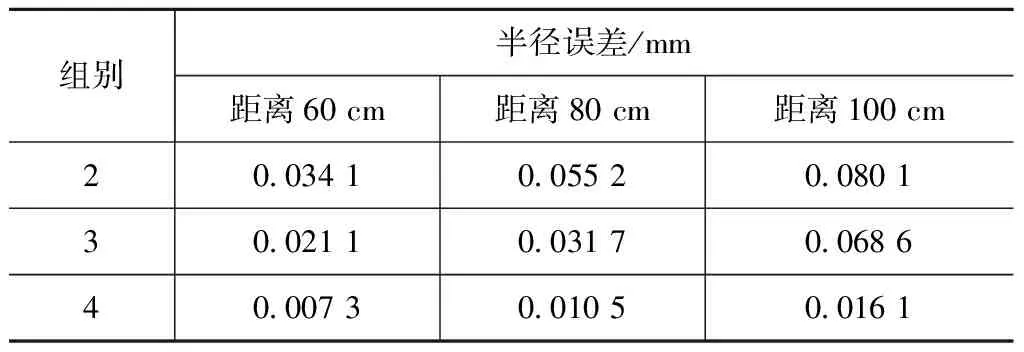
表3 半径计算误差

根据前文实验结果，取相机与被测物体距离55 cm，曝光亮度0～50，实验采集的不同圆孔结果如图9所示，圆孔测量效果如图10所示。为便于人眼识别，对图10增大对比度，结果如图11所示。

用标定板标定获得的像素当量0.158 1 mm，标定总体误差0.010 5 mm，半径的平均长度15.834 0像素。对小圆孔进行测量，得到其半径长度15.735 3像素，算得其半径的物理长度2.487 8 mm。对大圆孔进行测量，因用标定板上的圆标定时其测量范围相对较小，测量区域变大时误差会随测量区域增大而增大，故当测量区域增大时需对测量结果进行误差补偿。测量误差增大的原因主要是像素数增加导致的累加误差。其中误差包括两种情况：一是随着测量区域增大向真值的负方向移动；二是向正方向移动。因此，误差补偿时需确定对像素当量的增加或减少，比较标定得到的半径长度与真实半径长度，若大于则减去补偿量，否则加上补偿量。本文实验时标定得到半径的物理长度2.503 4 mm，小于真实半径长度2.514 mm，误差补偿时应加上补偿量。具体补偿方法如下：先用标定总体误差除以半径的平均长度，得到每个像素的误差补偿量0.000 631 mm。设半径为r，像素当量为m，半径像素长度为r1，补偿量为n，则补偿后的实际的半径长度r=r1(m+n)。可算得大圆孔的半径长度70.574 4像素，补偿后半径实际长度11.202 3 mm，误差0.012 3 mm。

4 结束语

本文提出了用一种改进的Zernike矩亚像素边缘检测和最小二乘拟合结合的方法检测圆孔参数，并分析了相机的曝光亮度，以及相机与被测物体距离对测量精度的影响。本文对传统Zernike矩亚像素细分算法进行了改进，提出了一种改进的Zernike矩亚像素边缘检测方法，研究了新的阈值判断条件，对亚像素细分的边缘点进行了细化和筛选，以使检测的边缘点更准确，圆的拟合时精度更高。研究发现：第一，在自然光环境中，相机与被测物体距离相同时，曝光亮度30～50的测量精度较好；曝光亮度一定时，相机与被测物体距离越近，测量精度越高。第二，机器视觉测量系统存在多种误差，故在测量时应根据需要进行误差补偿以消除或减小误差。本文分析了测量区域增大时误差变大的原因，并给出了误差的补偿方法。实验证明采用误差补偿后可获得较高的测量精度。第三，影响本文方法测量精度的因素主要有四个，一是获取图像边界的对比度，对比度越大测量精度就越高；二是相机与物体的距离，距离越近图像分辨率越高，测量精度越高；三是测量范围，测量范围变大时，由于镜头畸变的因素，测量精度会降低；四是被测物体孔径，被测物体孔径增大时测量精度将降低。本文的视觉测量系统易于实现，适于一般的测量环境，在实际检测中精度可达0.02 mm，实现了圆孔参数高精度的测量，对实现快速高精度的工业圆孔检测有重要的意义。

[1] 吴德刚, 赵利平. 基于机器视觉的圆孔尺寸测量系统研究[J]. 应用光学, 2013, 34(6): 1014-1018.

[2] 鲍晨兴, 王磊, 李凯, 等. 基于CCD的叶片气膜孔快速检测技术研究[J]. 航空精密制造技术, 2017, 53(2): 52-54.

[3] 何永辉, 王康健, 石桂芬. 基于机器视觉的高速带钢孔洞检测系统[J]. 应用光学, 2007, 28(3): 345-349.

[4] 陈会, 密保秀, 高志强. 基于畸变规律的三维结构光测量系统标定[J]. 光学学报, 2013, 33(12): 1215002.

[5] 段振云, 王宁, 赵文辉, 等. 基于点阵标定板的视觉测量系统的标定方法[J]. 光学学报, 2016, 36(5): 0515004.

[6] 刘子腾, 白瑞林, 王秀平. 视觉标定中圆心投影点精确定位[J]. 激光与光电子学进展, 2015, 52(9): 091001.

[7] HU T, WU H L, LIU G D. Study of micro-vision calibration technique based on SIFT feature matching[C]// The 5th International Conference on Computer and Computing Technologies in Agriculture. Beijing: [s. n.], 2012: 270-276.

[8] ROBERTS L G. Machine perception of three-dimension solids[M]. Cambridge: MIT Press, 1965.

[9] PREWITT J M. Object enhancement and extraction[M]. New York: Academic Press, 1970.

[10] MARR D, HILDRETH E C. Theory of edge detection[C]// Proceedings of the Royal Socity. London: [s. n.], 1980, B207: 187-217.

[11] CANNY J. A computational approach to edge[J]. IEEE Trans PA-MI, 1986(8): 679-698.

[12] LYVERS E P, MITCHELL O R. Subpixel measurements using a moment-based edge operator[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1989, 11(12): 1293-1307.

[13] GHOSAL S, MEHROTRA R. Orthogonal moment operators for subpixel edge detection[J]. Pattern Recognition, 1993, 26(2): 295-306.

[14] 李金泉, 王建伟, 陈善本, 等. 一种改进的Zernike正交矩亚像素边缘检测算法[J]. 光学技术, 2003, 29(4): 499-503.

[15] 高世一, 赵明扬, 张雷, 等. 基于Zernike正交矩的图像亚像素边缘检测算法改进[J]. 自动化学报, 2008, 34(9): 1164-1167.

[16] 祝宏, 曾祥进. Zernike 矩和最小二乘椭圆拟合的亚像素边缘提取[J]. 计算机工程与应用, 2011, 47(17): 148-150.

[17] 丁兴号, 邓善熙, 杨永跃, 等. 基于空间矩和Zerinke矩的亚像素边缘检测[J]. 应用科学学报, 2004, 22(2): 191-194.

[18] 魏本征, 赵志敏, 华晋. 基于改进形态学梯度和 Zernike 矩的亚像素边缘检测方法[J]. 仪器仪表学报, 2010, 31(4): 838-844.

[19] 崔继文, 谭久彬. 基于 Zernike 矩的亚像素边缘定位算法[J]. 光学技术, 2005, 31(5): 779-782.

[20] 胡树杰. 基于Zernike矩的亚像素边缘检测改进算法[J]. 制造业自动化, 2012(9): 4-6.

[21] LIU X D, EHRICH R W. Subpixel edge location in binary images using dithering[J]. IEEE Trans on Pattern Analysis and Machine Intelligence, 1995, 17(6): 629-634.

[22] 杨浩, 裴蕾, 李昌顺. 基于Zernike矩亚像素边缘检测的快速算法[J]. 光学学报, 2011, 28(11): 4831-4835.

ResearchonParametersMeasurementMethodofHighPrecisionCircleHoleBasedon
SubpixelEdgeDetection

QIAN Bin1， GUO Guo-qiang2， QIU Lei1， WANG Fu-wei1， JIN Lu1， FU Yan-jun1

(1. Key Laboratory of Nondestructive Testing (Ministry of Education), Nanchang Hangkong University, Nanchang 330063, Jiangxi, China;2. Shanghai Spaceflight Precision Machinery Institute, Shanghai 201600, China)

In order to improve the measurement results and reduce the error using machine vision, a high accuracy measurement method of circle hole parameters based on subpixel edge detection was studied in this paper, which was to calibrate the pixel equivalent on the base of circle calibration plate. The edge points were further refined and filtered using an improved Zernike moment subpixel edge detection method. The 5×5 plate was taken place by the 7×7 plate. The new threshold judgment criterion was designed to detect the subpixel edge. The deviation pixel detected of the edge was suppressed to obtain more accurate picture edge. The circle parameters were gained by circle fitness using the least squares method. The process of the improved method proposed was presented. The effect of the camera exposure brightness and the distance between the camera and the measured object on the measurement result was discussed by the experiment. The results show that the improved method has a strong ability to adapt to the environment and is easy to be realized. The measurement accuracy is high when the exposure brightness is 30～50. The measurement accuracy can reach 0.02 mm when the distance between the camera and object is 50～60 cm. The method proposed has wide application prospect in high precision industrial inspection.

circle hole parameters measuring; Zernike orthogonal moment; subpixel edge detection; the least squares fitness; calibration plate; pixel equivalent; exposure brightness; edge point

1006-1630(2017)06-0126-07

TP391.4

A

10.19328/j.cnki.1006-1630.2017.06.020

2017-06-08；

2017-11-07

国家自然科学基金资助(61661034)；江西省自然科学基金资助(20161BAB206116)；江西省重点研发计划资助(20171BBE50012)；上海航天科技创新基金资助(SAST2015046)；南昌航空大学研究生创新基金资助(YC2016052)

钱 斌(1993—)，男，硕士生，主要研究方向为三维测量、光电测试技术、信号与信息处理、机器视觉等。