电磁脉冲对MOSFET的热损伤效应研究

居培凯，徐建明，贾 巍，曹 兵

(1.南京理工大学 机械工程学院,江苏 南京 210094； 2.上海空间电源研究所,上海 200245)

电磁脉冲对MOSFET的热损伤效应研究

居培凯1，徐建明2，贾 巍2，曹 兵1

(1.南京理工大学 机械工程学院,江苏 南京 210094； 2.上海空间电源研究所,上海 200245)

针对金属氧化物半导体场效应管(MOSFET)在电磁脉冲作用下的热损伤问题，提出了一种新的热分析方法，通过仿真漏极注入阶跃脉冲下器件内部的温度响应研究了其损伤机理和规律。基于热效应半导体基本方程和热流方程，建立了用于仿真的器件模型和数值模型。采用注入法，以阶跃脉冲信号为输入，仿真研究了不同偏压上升时间和幅值下的器件损伤。结果发现：阶跃脉冲电压幅值一定时，MOSFET器件内部的温升过程及最后达到的最大温度与脉冲上升时间无关，器件在经过雪崩击穿、电流模式二次击穿后，温度迅速上升直至器件烧毁，烧毁所用时间与脉冲上升时间满足线性关系；脉冲上升时间一定时，器件温升随电压幅值增加而明显加快，器件能达到的最高温度也随之增加，器件烧毁所需时间与电压幅值的大小满足幂函数关系。研究对MOSFET的电磁脉冲毁伤机理认识和加固防护设计有一定的参考价值。

金属氧化物半导体场效应管； 电磁脉冲； 热损伤效应； 注入法； 阶跃脉冲； 偏压上升时间； 偏压幅值； 器件温升

0 引言

随着电子系统面临的电磁环境日益恶化，半导体器件越来越易受到电磁脉冲(EMP)的干扰和损伤。作为最基本的半导体器件，MOSFET被广泛用于模拟和数字电路，在电子工业中占主导地位，因此研究MOSFET在电磁脉冲作用下的损伤效应有十分重要的意义。目前，对MOSFET损伤的研究主要集中于静电放电对MOSFET的损伤。文献[1]通过对MOSFET进行二维模拟，研究了MOSFET在静电放电作用下的失效机制；文献[2]在分析静电放电失效机制的基础上对器件电学进行了模拟分析。关于高功率微波损伤效应的研究，文献[3]通过实验研究了在注入功率和频率变化条件下的器件微波干扰效应，探讨了微波作用前后器件特性变化及可能的损伤机理。文献[4]对MOSFET在高功率微波作用下的输出特性及器件内部的响应进行了数值模拟，分析研究了MOSFET损伤的一般规律。上述研究主要从电学角度分析了MOSFET的失效机理，但大部分情况下电磁脉冲对MOSFET损伤的本质是电磁脉冲引起的能量耦合，造成器件内部温度上升，以致失效。因此，有必要从热效应的角度研究MOSFET在电磁脉冲作用下的损伤效应。为此，本文基于半导体仿真软件，通过器件-电路联合仿真对电磁脉冲作用下MOSFET内部的温度响应进行了模拟，分析研究了器件的电磁脉冲热损伤机理及规律。

1 理论分析

MOSFET器件损伤机理的多样性使精确确定损伤的类型有一定难度，但MOSFET器件的大部分损伤均是由于其特定区域的温度达到了损伤温度，才出现了短路、熔断、扩散或熔化等永久失效的现象，最终都表现为热损伤。因此，可通过对器件的热瞬态效应进行分析，进而确定器件的损伤机理和整个损伤过程。

设器件中的电场强度为E，电流密度为J。电场的能量最终都会转为热量，并积淀于器件内，其大小取决于J，E。一般情况下，不考虑热效应时，仿真分析需计算半导体基本方程为电子和空穴的连续性方程、电流密度方程和泊松方程，这些方程既可统一描述半导体各区域载流子分布和运输状况，又能描述半导体各区域的场强与电势分布。考虑热效应时，需引入晶格温度变量作为新状态变量，可由求解热方程得到。因此，电热模型需同时求解晶格的热方程，以及电子和空穴的连续性方程、电流密度方程与泊松方程。

1.1 热效应半导体基本方程

因引入晶格温度变量，电流方程和泊松方程会有改变。电场和温度场耦合作用下的电流密度方程可分别表示为

Jn=qnμn·E+qDn·T

(1)

Jp=qnμp·E+qDp·T

(2)

当晶格温度在空间为非均匀的常数分布时，本征费米能级随温度而变，此时泊松方程为

(3)

(4)

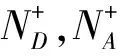
1.2 热流方程

热传导方程可表示为

(5)

式中：ρ，c，λ分别为材料的质量密度、比热比和热导率；Q为热产生密度。式(5)表明了晶格温度与时间在热源作用下的相互关系。

考虑与否载流子能量平衡方程，Q的表达式形式不同[6]。

a)不考虑载流子的能量平衡方程时，热主要来源于电流流过器件电阻时产生的功耗，半导体内部热产生密度

Q=Qn+Qp+Qu

(6)

Qn=Jn·En

(7)

Qp=Jp·Ep

(8)

(9)

b)考虑载流子的能量平衡方程时，除考虑外加电场对载流子所做的功及载流子净复合引起的能量变化外，半导体内部的热产生密度需考虑电子和空穴定向移动引起的能量变化。此时电热模型可用ψ、n、p、电子温度Tn、空穴温度Tp和晶格温度TL6个状态变量描述半导体状态均为时间和空间的函数[7]。载流子的能量方程为

(10)

(11)

此时的热传导方程可表示为

(12)

(13)

式中：下标L表示晶格；W为动能密度；S为能流密度；-·Sn，-·Sp为由相应载流子定向移动引起的能量变化；Uw为由载流子的产生与复合，以及通过声子、晶格交换能量引起的动能净损失率；λ为热导率；τ为能量弛豫时间。

当处于非绝热时，热载流子效应可忽略不计，此时认为载流子与晶格处于热平衡状态，温度相同，有Tn=Tp=TL=T[8]。同时忽略由电子和空穴的净复合率，以及载流子的定向移动引起的能量变化，热产生密度表达式可简化为

Q=Qn+Qp=J·E=Jn·En+Jp·Ep

(14)

2 仿真模型

2.1 器件模型

本文仿真所用的MOSFET结构如图1所示。图1中：从源区到漏区的水平方向为X的正向；S，G，D分别为晶体管的源极、栅极和漏极；N+为N型重掺杂的源区和漏区。杂质分布如图2所示。图2中：沟道长度1 μm，掺杂为高斯分布，结深0.3 μm，浓度峰值2×1017cm-3；P型衬底厚度2 μm，掺杂浓度5×1016cm-3。源漏掺杂均为高斯分布，结深0.2 μm，浓度峰值1.5×1020cm-3；半导体衬底的晶格温度恒定为300 K，并假定MOSFET与外部环境的热传导为零。整个结构的掺杂分布如图2所示。

2.2 数值模型

本文用Silvaco-TCAD模拟电磁脉冲作用下MOSFET的损伤过程，模拟损伤的过程需考虑器件的自热效应，计算由自热引起的器件温度分布需求解方程

(15)

式中：CL为晶格热熔；Pn，Pp分别为电子和空穴绝对热电功率；Ec，Ev分别为导带底和价带顶能量[9]。

在强电磁脉冲作用下，器件内部局部电场很高。除考虑掺杂浓度和载流子散射对迁移率的影响外，本文还考虑了高电场对迁移率的影响。迁移率模型选用Canali迁移率模型的扩展模型，有

(16)

式中：μlow为低场迁移率，考虑了载流子散射和温度对迁移率的影响；β为与温度有关的参数；Fhfs为准费米势梯度；α为参数，取α=0；vsat为室温下饱和漂移速度，取vsat=1.9×107cm/s[10]。

载流子的产生复合过程考虑了Shockley-Read-Hall复合及载流子雪崩击穿模型。此外，还考虑了源、漏极由高浓度掺杂引发的载流子隧穿效应。

3 仿真结果与分析

EMP包括了静电放电、高功率微波、核电磁脉冲和雷电电磁脉冲等多种形式。在实际工作环境中EMP作用于器件的波形非常复杂，阶跃脉冲信号虽不能表示实际工作中的复杂波形，但它不仅利于通过二维仿真软件研究其烧毁机理，而且利于计算器件的损伤阈值，故本文采用阶跃脉冲信号作为输入[11]。

对上述器件结构，在源极和衬底接地条件下，本文对MOSFET漏端施加不同上升时间、不同幅值的阶跃脉冲电压信号。栅极加2 V电压保证沟道开启，器件可正常工作。为更明确分析器件内部温度的变化，此处在脉冲源与器件的漏端间串联了阻值100 Ω的电阻，观察器件内部温度的变化。器件-电路联合仿真中，考虑器件自热效应，由计算器件半导体的基本方程和热流方程，可得器件内部晶格温度的分布，以器件中局部温度达到1 688 K的硅熔点作为器件烧毁判据[12]。仿真电路如图3所示。

因本文主要研究不同参数电磁脉冲对MOSFET的热损伤效应，为便于定量研究，设定栅极电压2 V，限流电阻100 Ω。不同栅极电压、外接电路对MOSFET发热量的影响，有待后续进一步研究。

3.1 不同偏压上升时间下器件损伤

为研究在不同上升时间偏压下MOSFET器件内部的损伤，设置阶跃脉冲电压V=13.6 V，分别在电压前沿上升时间0.5，1.0，5.0，10.0，15.0，20.0 ns下加载，仿真所得器件内部晶格的温升如图4所示。

由图4可知：在不同上升时间电压加载下，器件晶格的温升曲线形状几乎一致，表明器件的温升过程相同；器件最后达到的最高温度趋近于相同(1 765 K)，可知器件可达到的最高温度与偏压的上升时间无关；在偏压上升时间结束后，偏压达到最大值，此时器件的温度快速上升，当注入的脉冲随时间增加而不断增强时，漏极扩散区与衬底间pn结的反偏程度也不断增强，空间电荷区的内建电场随之增大，当漏极电压增加到一定程度后，该pn结开始发生雪崩倍增效应，随着注入功率进一步增大，器件发生寄生晶体管击穿效应，出现负阻现象，电流倍增，电流模式二次击穿发生，在电场和电流的双重作用下，器件内部热量积累、局部过热，器件温度达到硅熔点1 688 K，出现热损坏而烧毁。以1 688 K作为器件烧毁的依据，可得不同偏压上升时间下器件的烧毁时间如图5所示。

对数据进行拟合，可得相应关系式为

y=107.308 5+0.789 3x1

式中：y为烧毁时间；x1为上升时间。x1，y的相关系数R2=0.999 ，表明其拟合精度较佳。

3.2 不同偏压幅值下器件损伤

为研究在不同偏压幅值下MOSFET器件内部的损伤，设置阶跃脉冲电压上升时间t=5 ns，分别在电压幅值13.6，15.0，20.0，30.0，40.0，50.0 V下加载，仿真所得器件内部晶格的温升如图6所示。

由图6可知：当偏压大于20 V时，器件内部温度上升明显加快，这是因为注入功率大小与电压大小的平方成正比，电压幅值的增加会显著加快器件的温升速度；随着偏压幅值的增加，器件最后达到的最高温度也随之增加，V=13.6 V时最大温度1 765 K，V=15 V时最大温度1 880 K，V大于20 V时器件温度达到了仿真设置的最大温度2 000 K。以1 688 K作为器件烧毁的依据，可得不同偏压幅值下器件的烧毁时间如图7所示。

对数据进行拟合，可得相应关系式为

y=(1.6×106)(x2)-3.7

式中：x2为电压幅值。x2，y的相关系数R2=0.99，表明其拟合精度较佳。

4 结束语

在电磁脉冲对MOSFET器件的损伤特性中，温度是衡量器件性能和可靠性的重要评估标准。本文对阶跃脉冲注入下MOSFET内部温度响应进行了数值模拟。研究表明：当阶跃脉冲电压幅值一定时，MOSFET器件内部的温升过程及最后达到的最大温度均与脉冲上升时间无关，器件在发生雪崩击穿后，随着注入功率的不断增大，电流模式二次击穿发生，随后温度迅速上升直至器件烧毁，烧毁所用的时间与脉冲上升时间满足线性关系；当脉冲上升时间一定时，器件的温升随电压幅值增加而明显加快，器件能达到的最高温度也随之增加，器件烧毁所需的时间与电压幅值的大小满足幂函数关系。以往研究针对半导体器件的研究主要应用器件模拟或电路模拟，本文综合了器件和电路模拟，更系统全面地仿真研究了MOSFET在电磁脉冲作用下的热损伤效应。因数值仿真只能为MOSFET器件的电磁脉冲毁伤机理研究和加固防护设计提供理论参考，为验证仿真的准确性，还需进行大量试验。关于电磁脉冲对半导体器件的毁伤效应，研究方法主要有注入法和辐照法，本文采用了注入法，后续研究可采用辐照法，通过对比分析修正MOSFET的损伤模型，从而建立电磁脉冲对MOSFET的毁伤评估准则。

[1] 郑若成, 孙峰, 吴金. NMOS器件ESD特性模拟[J]. 电子与封装, 2008, 59(8): 18-21.

[2] 李永坤, 郝跃, 罗宏伟. ESD电热模拟分析[J]. 封装、测试与设备, 2007, 32(1): 77-81.

[3] KIM K C, ILIADIS A A, GRANATSTEIN V. Study of the effects of microwave interference on MOSFET devices in CMOS integrated circuits[J]. Semiconductor Device Research Symposium, 2003, 10: 530-531.

[4] 李勇, 谢海燕, 杨志强, 等. 高功率微波作用于金属氧化物半导体场效应管响应[J]. 强激光与粒子束, 2015, 27(10): 103242.

[5] ANGHEL C, GILLON R, LONESCU A M. Self-heating characterization and extraction method for thermal resistance and capacitance in HV MOSFETs[J]. IEEE Electron Device Letters, 2004, 25(3): 141-143.

[6] STRATTON R. Semiconductor current-flow equations (diffusion and degeneracy)[J]. IEEE Trans on Electron Devices, 1992, 19(12): 1288-1300.

[7] MAYARAM K, CHEM J H, ARLEDGE L, et al. Electrothermal simulation tools for analysis and design of ESD protection devices[J]. IEEE International Electron Devices Meeting, 1991, 11: 909-912.

[8] 马振洋, 柴常春, 任兴荣, 等. 不同样式的高功率微波对双极晶体管的损伤效应和机理[J]. 物理学报, 2013, 62(12): 128501.

[9] 柴常春, 席晓文, 任欣荣, 等. 双极性晶体管在强电磁脉冲作用下的损伤效应与物理机理[J]. 物理学报, 2010, 59(11): 8118-8124.

[10] KEVIN F, KRISHNA S. Electrothermal effects during unclamped inductive switching (UIS) of power MOSFET’s[J]. IEEE Transactions on Electron Devices, 1997, 44(5): 874-878.

[11] 邵立汉, 夏同生. 沟道宽度对MOSFET高功率微波效应的影响[J]. 固体电子学研究与进展, 2014, 34(5): 421-425.

[12] 游海龙, 蓝建春, 范菊平, 等. 高功率微波作用下热载流子引起n型金属-氧化物-半导体场效应晶体管特性退化的研究[J]. 物理学报, 2012, 61(10): 108501.

ResearchonThermalDamageEffectofMOSFETunderEMPInjected

JU Pei-kai1， XU Jian-ming2， JIA Wei2， CAO Bing1

(1. School of Mechanical Engineering, Nanjing University of Science and Technology,Nanjing 210094, Jiangsu, China; 2. Shanghai Institute of Space Power-Source, Shanghai 200245, China)

Aiming at the damage of metal-oxide-semiconductor field-effect transistor (MOSFET) under electromagnetic pulse (EMP) injected, a new thermal analysis method was put forward in this paper. The damage mechanism and regulation were studied by simulating the internal temperature response of MOSFET under the EMP injected into the drain electrode. According to the general equation and heat flux equation of semiconductor based on thermal effect, the device model and numerical model were established for simulation. Using injected method, the device damage under various rise time and amplitude of voltage was analyzed through simulation when the step pulse signal was input. The results showed that the internal temperature rose process and the maximum temperature in MOSFET device had nothing to do with the pulse rise time when the voltage amplitude of step pulse was fixed. After the avalanche breakdown and current mode second breakdown, the device temperature raised rapidly until the device was burned. The burnout time and pulse rise time were satisfied linear relationship. When the pulse rise time was stayed the same and the rise of temperature in the device was speeded up with increasing of the voltage amplitude. The highest temperature that the device can achieve also increased. The burnout time of the device and voltage amplitude satisfied power function relationship. The study has some reference valuable for the mechanism research of EMP damage of MOSFET and the reinforcement and protection design.

metal-oxide-semiconductor field-effect transistor (MOSFET); electromagnetic pulse (EMP); thermal damage effect; injected method; step pulse; voltage rise time; voltage amplitude; internal temperature rise

1006-1630(2017)06-0120-06

TN386.1

A

10.19328/j.cnki.1006-1630.2017.06.019

2017-03-31；

2017-08-14

居培凯(1989—)，男，硕士生，主要研究方向为电磁脉冲毁伤及其防护技术。